公路坡度差对车辆尾气排放的影响分析
2022-02-25贾兴利秦雪芳周吴啸李双庆陈星澎
贾兴利, 秦雪芳, 周吴啸, 李双庆, 陈星澎
(长安大学公路学院, 西安 710064)
生态环境部颁布的《中国机动车环境管理年报(2018)》[1]表明,机动车污染问题日益突出,机动车尾气排放已成为中国交通大气污染的主要来源之一。与平坡路段相比,机动车在纵坡路段行驶时,需要克服高差,会消耗更多的油耗,排放更多的尾气,对生态环境造成很大威胁,高速公路纵断面是机动车产生高排放的路段[2]。机动车在不同的道路线形上行驶时,通过不断地调整车辆运行状况以适应道路线形的变化。道路线形的差异会导致车辆的运行状况变化,进而会影响车辆的尾气排放状况。因此,研究道路线形变化对车辆尾气排放的影响是十分有必要的。
Dong等[2]通过实际数据研究圆曲线半径大小对碳排的影响,得到影响车辆碳排的最小圆曲线半径大小为500 m的结论。许金良等[3]运用MOVES(motor vehicle emission simulator)模型得到载重柴油车在小半径圆曲线路段上的累积碳排放量预测模型。Jia等[4-5]通过研究纵坡与碳排之间的量化关系,研究发现当纵坡坡度值大于3%之后碳排显著增加,并通过实例研究提出一种碳排与纵坡之间的预测模型。Kang[6]通过研究路线几何设计的方法来降低汽车油耗并增加车辆的行驶安全性。Ko等[7-8]分别对纵坡坡度大小以及竖曲线曲率对车辆碳排进行了研究,并得出几何线形对碳排有着重要影响。Loulizi等[9]研究量化燃油消耗和坡度之间的关系,并利用GIS工具在设计阶段对公路进行多指标的评价筛选,最后通过实例证明过筛选而建设的公路燃油消耗会有所降低。
中外学者对低能耗、低污染为基础的低碳公路交通进行了大量的研究。明确道路平面路段和纵坡路段对汽车尾气排放水平的影响规律,对于绿色公路设计有着重要意义。但是关于低碳公路路线优化设计研究成果多是定性、宏观层面的指导性原则,对竖曲线路段几何指标与碳排放映射关系分析缺乏。此外考虑到中国小客车数量远大于货车数量,因此以小客车为研究对象,从微观视角出发,选择MOVES模型进行车辆尾气排放量预测,以凸形竖曲线路段为例,进行不同坡差与车辆尾气排放水平相关关系的探究。
1 数据获取及MOVES参数修正
1.1 MOVES模型
鉴于实验道路线形样本数量的局限性,本文中采用实验仿真的手段预测车辆尾气排放量,用实测实验对模型预测值进行验证。
美国环保局开发的综合移动源排放MOVES模型与COPERT(computer program to calculate emissions from road transport)、MOBILE(the MOBILE highway vehicle emission factor model)及IVE(international vehicle emission model)等机动车排放模型相比,将瞬时加速度与瞬时速度相结合来反映车辆的运行状况,更准确地反映了车辆在实际操作中的排放特征。故本文中选择MOVES模型进行不同坡差情况下的凸形竖曲线路段车辆尾气排放的预测[10-12]。
1.2 参数本地化修正
由于MOVES模型中的数据库是以美国各州县机动车尾气排放数据为依托而建立的,不适用于直接预测和分析我国机动车碳排放水平。故本文通过调查我国实际的交通状况、道路类型、车辆、燃油等信息,修正了MOVES模型在微观层次上所需输入的参数[13-15]。其修正后参数设置如下。
(1)模拟层次:微观层次。
(2)模型年份:将中国第六阶段机动车污染物排放标准与美国的标准做对比,确定模拟年份为2009年。
(3)道路类型:本文中选择MOVES模型中代码为2的道路类型,代表道路为高速公路。
(4)地理信息:本研究从影响模型计算的年均降水量、海拔、经纬度、平均气温、相对湿度等因素出发,将陕西省西安市与美国各州的情况做对比,确定以Georgia的Fulton县作为模拟地理区域,气候对比见表1。

表1 西安与Fulton气候对比
(5)排放源类型:据统计汽车占中国机动车主导地位[1],故文中选择小客车作为主要排放源,对应MOVES模型中排放源类型代码为21。
(6)燃油类型:据年报统计[1],中国机动车按燃料类型分类,汽车是污染物排放总量的主要来源之一,故本文中选择汽油作为燃油类型。
(7)车龄:选择机动车的平均车龄为3年,对应MOVES模型中的车龄代码为3。
(8)运行工况:为了估算机动车的排放水平,必须结合机动车的瞬时比功率(vehicle specific power,VSP)和瞬时速度查找机动车的逐秒运行状况代码,将车辆的运行状态与运行工况相匹配。最后运用MOVES模型获得每个运行工况下机动车尾气排放量。比功率VSP的计算表达式[16]为
PVS=v(1.1a+0.132)+0.000 302v3
(1)
式(1)中:PVS为机动车比功率,kW/t;a为机动车瞬时加速度,m/s2;v为机动车瞬时速度,m/s。
1.3 速度预测及多项式模型
研究中凸形竖曲线中点运行速度的预测模型计算公式[17]为
(2)
式(2)中:K为竖曲线曲率,m/%,文献[18]规定最低标准K=39 m/%。
然而车辆不会在竖曲线上以恒定速度行驶。为了考虑曲线上的速度变化,利用多项式模型得到沿行驶距离和时间的逐秒速度[19-20],即
a(t)=ramaxθ(1-θm),m>-0.5
(3)
式(3)中:a(t)为车辆逐秒加速度, m/s2;amax为最大加速度,m/s2;θ=t/ta,为自开始加速的时间t与总加速时间(ta)的比值;总加速时间可由加速度时间回归方程求得,即
(4)
m、r为参数。m、r和am的计算公式为
(5)
(6)
(7)
式中:Va、Vi和Vf分别表示机动车加速行驶中的平均速度、初始速度和最终速度,km/h;x(t)表示时间t小客车行驶距离,m。时间t的速度和距离公式为
(8)

(9)
1.4 试验方案
为了验证仿真试验数据的有效性,取西安绕城高速公路K0-100~K29+100段为试验路段。为了保证速度与油耗实测数据的准确性,所选试验路段纵坡度应保持一致,纵坡段越长越好,以求能达到稳定车速﹔车辆运行处于自由流状态;试验日选择天气状况良好的气候条件,尽量消除道路平面、横断面及其他影响因素的影响。
试验车辆选择宝沃BX5作为试验车,选择沈阳广成科技有限公司研发的USBCAN(universal serial BUS controller area network)总线分析仪,读取汽车CAN(universal serial BUS)总线原始数据,使用CAN总线专用调试分析软件ECAN tools软件获取车辆速度、油耗量。采用使用IPCC方法将试验收集到的油耗数据转化为碳排放量。
IPCC碳排放核算公式为
W=NPCKρ
(10)
XCO2=EW
(11)
式中:XCO2为二氧化碳核算值,kg;E为燃料消耗量,L;N为平均低位发热量,kJ/kg;P为潜在碳排放系数,t/TJ;W为碳排放因子,kgCO2/kg;C为碳氧化率,%;K为转换系数,K=44/12;ρ为密度参数,kg/L。
中国汽油碳排放系数及相关数值的计算公式为
F=PCK=68 607 kg/TJ
(12)
W=NF=2.954 9
(13)
每升汽油的碳排放系数为
q=Wρ=2.216
(14)
2 基于MOVES的尾气排放数据库模拟
2.1 方案设计
凸形竖曲线路段的运行工况与前后线型有关,为反映坡差对机动车尾气排放量的影响,本文中假定凸形竖曲线路段处的线型形式为直线-竖曲线-直线。运用速度预测模型和多项式模型得到车辆在竖曲线路段瞬时速度和加速度。
Barth等[20]研究表明:当车辆速度高于105 km/h或低于72 km/h时,比以稳态速度行驶(72~80 km/h)时的油耗和尾气排放量高。故本文将起始速度设置为105 km/h,研究小客车在不同坡差下凸形竖曲线路段的尾气排放,规定凸形竖曲线的路段长度为300 m,其中前后坡长度分别设置为150 m。不同的坡差对应不同的坡度组合,根据不同坡差制定详细的模拟方案,如表2所示。

表2 坡差模拟方案
2.2 速度和运行工况分布
以起始速度为105 km/h的小客车作为研究对象,在坡度组合为-2-6.5的纵坡上行驶。运用式(12)计算小客车在竖曲线路段的逐秒速度,运用式(1)得到小客车逐秒VSP,然后进行机动车的运行工况区间的划分。以坡差为-3%,坡度组合为前坡1.5%、后坡-1.5%为例,逐秒的速度与运行工况分布如表3所示。

表3 坡度组合为1.5-1.5的运行工况分布
2.3 坡差与车辆尾气排放关系
MOVES是基于瞬时车速和车辆比功率,将运行废气排放预测的运行模式分为23个运行工况区间。由于MOVES没有直接报告每个运行工况的排放量,本研究采用微观层次进行项目级分析,采用单个运行模式分布(即目标运行工况区间分布比例为1,其余为0)。通过改变目标运行工况区间,重复操作获得了所需的各个运行工况的排放率。根据对行驶时间内逐秒的速度曲线下每个运行工况区间的尾气排放进行汇总得到总排放量。表达式为
(15)
式(15)中:Etype是二氧化碳(CO2)、一氧化碳(CO)、氮氢化合物(NH3)、氮氧化物(NOx)的总排放量;Etype,bin是时间t内小客车所在运行工况的废气排放量。基于MOVES模型得到高速公路不同坡差情况下竖曲线段的尾气排放数据库。图1为不同坡度组合下CO2、CO、NH3、NOx排放量对比图。

图1 不同坡差下各气体排放量
从图1(a)可以看出,当前坡坡度一定时,在坡度差小于-3时小客车在规定长度竖曲线上的CO2排放量随着坡度差代数值的增大而增大。当坡度差代数值大于3时,CO2排放量增加幅度变大,当坡度差为-6时,CO2排放量突然下降,然后继续上升且上升幅度变小。从图1中可以看出,4种排放物的排放量均随坡差代数值的增大而上升。主要是由于在凸形竖曲线段前后坡度差越大,机动车的发动机负载越大,行驶过程中产生的CO2等尾气排放量就越多。小客车在不同坡差的竖曲线行驶会极大地影响尾气排放,当速度增加时,对发动机牵引力的要求也会增加,导致汽车的尾气排放量大幅度的上升。在四种主要排放物中,CO2排放量最大,依次是CO、NOx、NH3排放量。
从图1中还能够看出,当坡差一定时,随着前坡坡度的增加,CO2、NOx、CO、NH3排放量基本不变,其中CO2最多增加14.7%,CO排放量最多增加23.3%。CO2、NOx、CO、NH3排放量随着坡差代数值的增加均呈上升趋势。其中,CO2排放量最大,其次依次是CO、NOx,NH3排放量最少。因此,本文中只对坡差和CO2排放量进行关系拟合。
2.4 碳排放预测模型建立
当坡差一定时,随着前坡坡度的增加,CO2、NOx、CO、NH3排放量几乎不变。故本文中取前坡坡度1.5%为例,用SPSS软件对坡差和CO2排放量的关系进行拟合分析,拟合关系对比如表4所示,坡差与碳排放拟合曲线如图2所示。为了更直观的展示凸形竖曲线路段,不同坡差对机动车碳排放量影响规律,本文中以单位竖曲线长度上的碳排放量作为因变量,进行坡差与碳排放量的拟合关系研究,表达式为
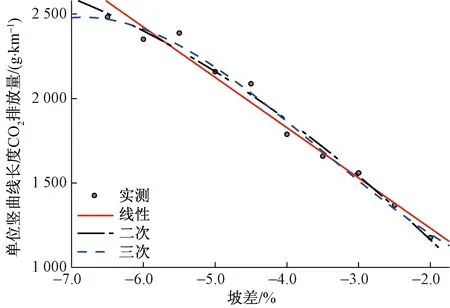
图2 坡差和碳排放量拟合曲线
(16)
式(16)中:E0为单位竖曲线长度上CO2排放量,g/km;Ec为竖曲线长度范围内小客车的总碳排放量,g;L为竖曲线长度,km。
根据赤池信息准则(akaike information criterion,AIC)和贝叶斯信息规则(Bayesian information criterion,BIC)准则对小客车的碳排放规律进行分析,结果显示坡差与小客车的碳排放量的拟合关系中,其非线性回归模型的拟合度较高。通过对单位竖曲线长度上小客车碳排量与坡差的关系进行拟合分析,结合AIC与BIC准则得到精度较高的一元回归模型。如表4所示,三种函数的F值较大,R2都接近1,方程回归显著拟合优度满足要求。
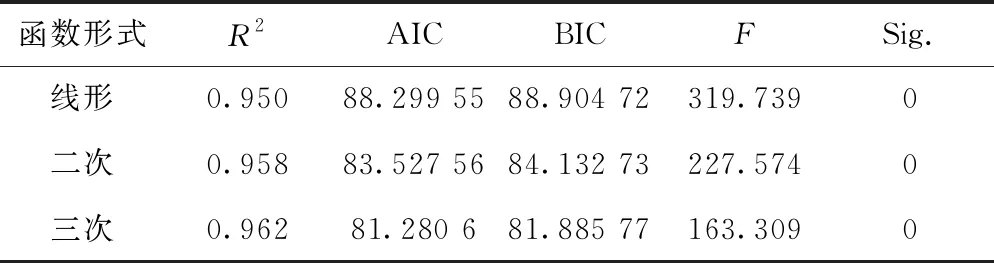
表4 坡差和碳排放量回归模型拟合效果对比
从表4可以看出,二次函数的AIC和BIC值较小,F值较大,能够确保拟合准确性。因此得到单位竖曲线长度上小客车碳排量与坡差的二次拟合关系,即
Ec=-493.105ω-22.955ω2+268.17
(17)
式中:Ec为不同坡差下单位凸形竖曲线长度上碳排放量;ω为坡差,ω=i2-i1。
2.5 模型验证
为了验证模型的适用性,取西安绕城高速公路K0-100~K29+100段的19个纵坡组合段,依据我国汽油车现状对应的碳排放核算方法,核算出实测油耗值相应的碳排放量。随机选择9个纵坡组合段,对比预测值与实测值,确切地评价该路段实际车辆的碳排放状况,如表5所示。

表5 模型预测值与实测值对比
通过计算,小汽车单位长度碳排放量实测值与模型预测值的平均相对误差为4.7%,小于10%,验证了模型的预测的有效性。
3 结论
(1)为适用于中国的实际道路交通与车辆条件,从地理信息、气候状况、车辆燃油特性等角度出发,对MOVES模型中的参数进行了本地化修正。
(2)以MOVES模型为基础,建立了小客车在凸形竖曲线路段不同坡差情况下的碳排放数据库,得出坡差代数值越大,小客车的尾气排放量越大;当高速公路坡差一定时,前坡坡度对小客车的尾气排放影响较小。在四种主要排放物中,CO2排放量最大,依次是CO、NOx、NH3排放量。
(3)利用SPSS软件对单位距离凸形竖曲线上CO2排放量与坡差进行关系拟合,得到单位竖曲线长度上坡度差与碳排放量的映射关系,以简便预测不同坡差情况下单位竖曲线路段的CO2排放量,最后利用实测数据验证了的模型的有效性。
(4)论文主要针对小客车进行凸形竖曲线路段坡差对车辆尾气排放量的影响,是否适用于其他类型的车辆和其他线形路段有待进一步的验证。
