基于滤波宽度动态调整的递推中值与外延算法
2022-02-25回朝妍贾梦涵马仡男佟美琪
高 宇,回朝妍,张 辉,贾梦涵,马仡男,佟美琪
(北京科技大学能源与环境工程学院,北京 100083)
0 引言
在工业生产和实验研究的控制系统中,需要对现场的相关物理量如温度、压力、液位等连续变化的数据进行采集和记录[1]。这些被测量以模拟量为主,因此需要将连续的模拟量转换为离散的数字量,然而,在数据采集过程中,信号源、传感器、放大电路、A/D转换模块等都会因噪声污染影响测量结果的准确性[2],并且在测定过程中也会出现未知干扰,使采集到的信号呈现不规则的随机波动,从而影响最终的检测结果。
在仪器控制系统中,常见的噪声为周期性噪声和非周期性奇异型噪声。为了提高测量的准确性,抑制噪声对检测结果的影响,可以采用数字滤波技术对采样数据进行滤波处理[3]。数字滤波技术不需要额外增加硬件设备,而是通过软件实现滤波,是一种常用的滤除噪声的数据预处理方法。数字滤波根据数学算法编写出相应的程序来对采集到的数据进行计算和转换,从而获得一组可靠性更高的数据。常用的数字滤波方法有限幅滤波、消抖滤波、算术平均值滤波[4]和中值滤波等[5]。
图1为采用不同滤波方法得到的数字滤波效果对比图,从图1中可以发现:图1(b)所示的限幅滤波[6]对于偶然出现的脉冲噪声有较强的抑制作用,可以将尖峰完全消去,但是无法处理周期性、小幅度的信号波动,并且滤波后的曲线呈一条直线完全丢失原始数据的特征信息,不同数据的脉冲噪声幅度大小不同,也会影响滤波的处理效果[7];图1(c)中,均值滤波不能处理偶然出现的脉冲型的干扰峰,计算得到的有效值会受到脉冲峰极值的影响,数据产生偏差,造成数据的上浮或者下沉;图1(d)所示的消抖滤波算法适用于缓慢变化的数据序列,不能处理快速变化的数据,并且会将采样数据最重要的特征峰消去,此外,处理后的数据呈阶梯状,平滑度差;图1(e)中的中值滤波算法处理得到的曲线光滑,噪声和尖峰都能被有效地去除,对比原始数据曲线,在滤波效果较好的情况下吻合度也较高[8]。通过对常见的滤波算法的优缺点进行分析,将递推算法和中值滤波算法相结合,并且对滤波宽度进行动态调整,改进后的滤波算法能够获得很好的滤波效果,并且能够依据数据自身基底特征对边界处的数据进行外延。
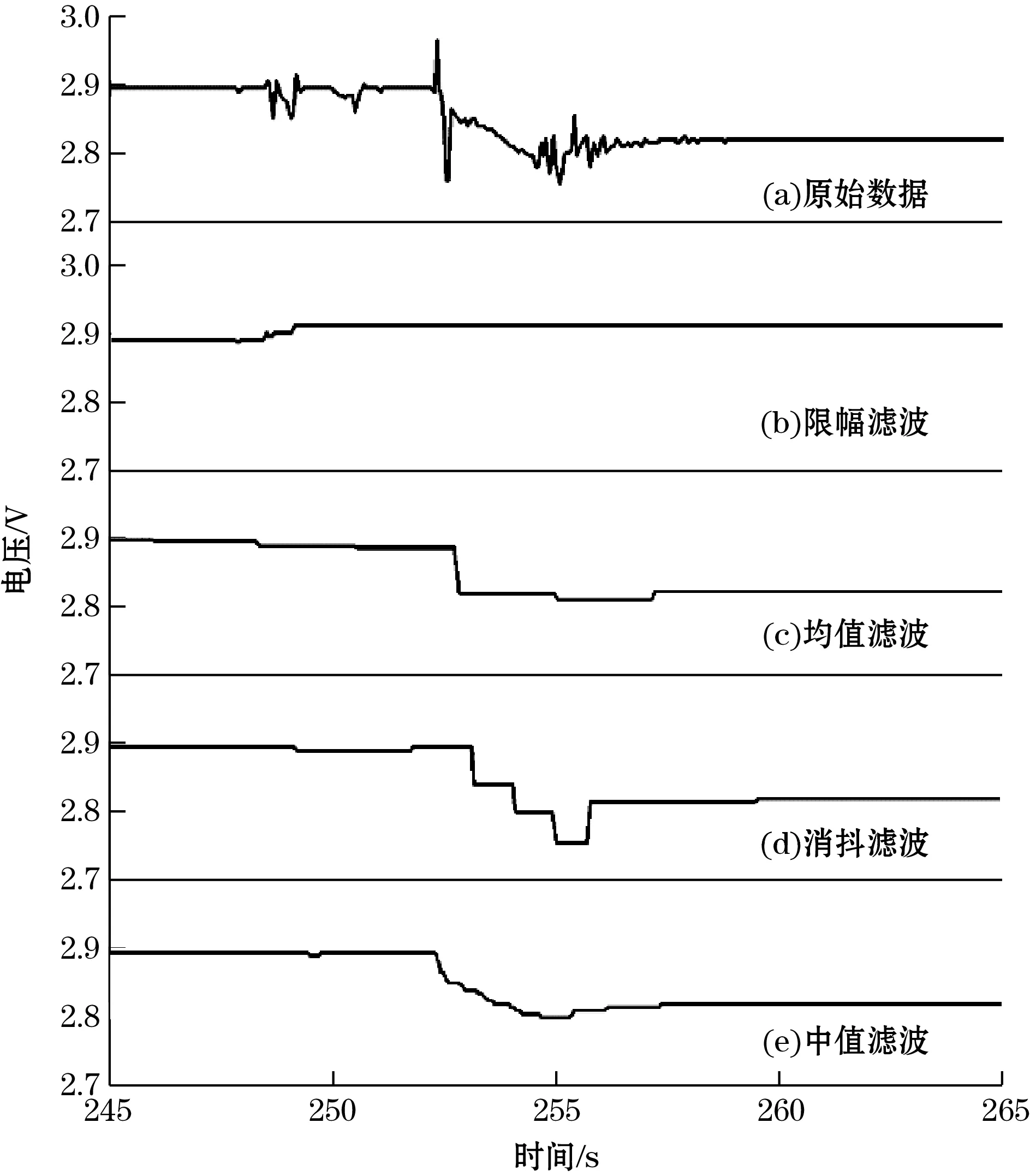
图1 数字滤波效果对比图
1 递推中值算法
中值滤波算法是一种基于统计排序理论的非线性滤波方法,其基本思路是连续读取N个(N一般为奇数,N=2L+1)采样值,然后将N个采样值按照大小排成有序数列,取有序数列的中间位置的值作为有效值输出,即经过滤波处理后输出的第k个数据为[k-L,k+L]的中位值。其中,排序算法可以采用“冒泡排序法”、“快速排序法”等常用算法。这种滤波算法能够很好地滤除由于偶然的外界因素干扰或者是传感器自身不稳定而形成的脉冲峰,并且还能够较好地保留原始数据的趋势和特征。
利用该算法进行数据处理首先设置递推队列长度N,即程序读取N个数据,运行中值滤波算法进行处理,排序得到当前N个数据序列中间位置对应数据的值,然后将其作为有效值输出。
将递推算法的思路与中值滤波结合,可实现精确滤波。如图2所示,首先建立可存放N(N=2L+1)个数据的递推队列,开始读取数据并且判断队列是否已经填充满。当队列填充满后,进行排序将当前队列中的中位值作为滤波后的有效数据输出;然后递推滑动队列后移一位,遵循先进先出的原则[9],剔除数据序列中的第一个数据,并且获取原始数据序列后一位的新数据,将其填充到队列中。保持队列长度N固定,再次进行中值滤波处理。依照这种方式依次滑动递推队列,直至将全部数据处理完毕。
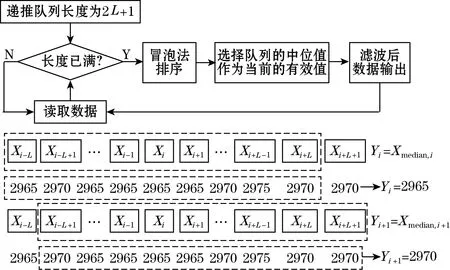
图2 递推中值滤波算法流程图
利用递推中值滤波算法可以对信号进行光滑处理。为了验证其光滑处理的效果,对中值滤波分别进行递推算法采样和分段采样的对比分析,均设置采样数N=31进行滤波处理,利用Origin绘制各自滤波处理后的数据曲线,所得结果如图3所示。

图3 分段中值与递推中值滤波效果对比图
可以看出分段中值滤波算法处理得到的数据明显呈阶梯状,光滑度较差。在图3(a)中,分段中值滤波在递推队列长度选择不当时,会出现不能有效去除噪声干扰的现象,并且图3(b)中,在特征峰部位峰谷极值点被滤除,出现了数据畸变失真,造成重要信号丢失,影响后续的数据处理。而递推中值滤波处理后的数据保持了原始数据的趋势,并且曲线光滑,数据准确度高。
图4为递推中值滤波算法主体程序图。算法使用C语言编写,图4左侧为程序的源代码,通过自定义数据结构将代码函数模块化,便于滤波处理功能的实现;右侧为对应的N-S流程图,采用顺序、选择和循环结构展示程序运行逻辑。

图4 递推中值滤波算法主体程序图
2 递推队列长度
2.1 参数选择
递推中值滤波算法除了需要获取原始被测量数据外,还需要设置递推队列长度N这一参数,递推队列长度影响滤波的处理效果[10-11]以及程序运行速度等性能。为分析递推队列长度的选择对滤波效果产生的影响,对比设置不同队列长度条件下的滤波处理结果,如图5所示。
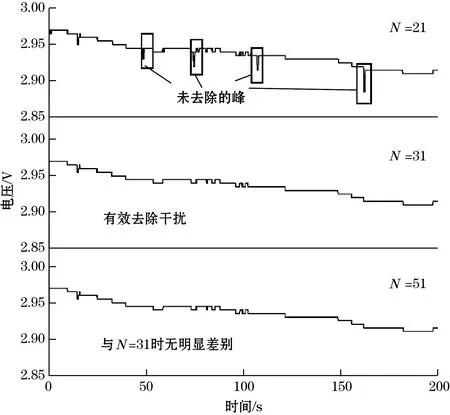
图5 不同递推队列长度滤波效果对比图
首先递推队列长度N=2L+1[12],当L设置为大于干扰峰的宽度时就可以将干扰峰全部滤除,当实验数据的特征峰宽度大于L时,特征峰就会在进行滤波处理的过程中保留下来,达到去除噪声和干扰的目的。图5为不同的递推队列长度滤波的效果对比图,可以看到当N=21时,滤波算法已经具备去除原始数据部分噪声的能力,但处理后的数据中仍存在宽度较大的干扰峰未被去除;当N=31时,可以有效地去除干扰;当N=51时,此时的滤波效果与N=31时无明显差别,但是递推队列长度设置过大时,可能会出现将原始数据中重要信号判定为干扰信号而去除的现象。因此,N设置较小时,除了对原始数据能够进行滤波外,还保留了一部分宽度较大的峰;随着递推队列长度的增大,大部分的峰都被滤除。综上,算法的分辨能力会受到递推队列长度的影响,即判定宽度小于L的峰为干扰信号将其消除,并保留宽度大于L的峰,防止了重要信号的缺失[13]。
2.2 动态调整
递推中值滤波算法的基本思路是选取一组数据的中位值作为有效值,剔除掉干扰附近的最大值和最小值,因此在特征峰的峰顶或者峰谷处会形成平台,出现峰高的损失为了保证数据的准确性,在应用递推中值滤波的过程中,需要检测峰顶或峰谷的位置对其进行数据还原。
核心算法N-S图如图6所示,当峰顶或峰谷经过滤波产生平台后,在定义的链表中记录平台的起始位置、结束位置以及平台宽度。在平台的起始点重新设置递推队列长度并且将其设置为平台宽度,从起始点开始之后的数据依次将递推队列长度递减,直至在平台中心处队列长度递减为1,即输出原始数据。此时,特征峰的峰高和峰位等重要信息得到保留和还原。然后将队列长度依次递增直至平台结束后,队列长度还原至初始设定值N,程序依据原始设定长度N利用递推中值滤波算法继续对数据序列进行滤波处理。处理完当前平台的数据后,链表指向下一个节点,获取下一个平台的信息,再次进行队列长度动态调整。这种算法保留了原始特征峰的峰高和峰位等重要参数。

图6 递推队列长度动态调整算法N-S图
该算法不仅需要对平台的信息进行记录,还需要对平台进行判定,即当滤波输出的相邻两次数据相同时,才将其判定为平台。在此基础上,利用flag_decline和flag_rise 2个状态变量判断曲线的变化趋势,将在峰顶处形成高于两侧数据的平台或者在峰谷处形成低于两侧数据的平台判定为需要进行动态调整的平台,并记录在链表中。
图7为递推队列长度动态调整示意图。从图中可以看出,当数据出现平台时,将起始点Xstart处队列长度调整为平台宽度width,然后递推队列长度开始递减;当到达平台中心处时,递推队列长度为1,此时输出的数据为队列中唯一的数据,即还原了采样值,同时平台的中心处通常对应于峰顶或峰谷的极值点;平台中心处之后数据的队列长度依次递增,直至平台结束点Xend处,递推队列长度增加至平台宽度。当递推队列处于上升或者下降趋势的曲线处时,滤波处理输出的数据就是排序后的中位值,此时与原始数据序列不存在位置上的偏移[14]。

图7 递推队列长度调整示意图
3 基底数据特征外延
递推中值滤波算法是将一组采样信号进行排序后选取中值作为序列中间位置的有效值输出,因此在数据的边界(即数据的开始和结尾处)会出现部分数据的缺失,为保证数据的完整性需要对其进行补充,数据补充可以通过数据拟合的方式实现。
根据数据离散的特征,提出使用最小二乘法对原始数据进行拟合并依据拟合结果获得原始数据序列的特征,然后对曲线进行预测以达到补充缺失数据的目的。最小二乘法是以残差平方和最小为条件进行求解得出参数的最佳值以及最佳函数方程[15]。将递推中值滤波算法与最小二乘法相结合,在边界数据部分利用最小二乘法对其进行运算,建立横坐标与纵坐标的函数关系,得到确定其基底特征的参数。
在求解拟合函数的过程中,首先取出边界处的N个数据,假设数据点间的函数关系满足线性变化规律,并且根据拟合函数计算出的值与实际数据的偏差平方和最小,此拟合函数用数学语言可描述为Y=kX+b,其中X是自变量,Y是拟合目标[16]。依据取得的N个数据确定一个最佳的拟合方程,计算出方程中的2个待定参数就能够确定原始基底数据的特征。根据建立的一元线性函数模型,将缺失的数据按基底特征进行计算补充。
将处理后的数据在Origin中绘制,其结果如图8所示。可以看到,对比原始数据,当仅使用递推中值滤波算法处理时,起始段与结尾段存在部分数据缺失;对原始数据采用最小二乘法拟合,获得其基底特征进行边界数据补充后,得到的数据曲线完整且光滑。

(a)起始段
递推中值滤波算法结合最小二乘法计算原始数据的特征并根据特征进行数据预测,不仅将经过递推中值滤波算法前后缺失的数据补充完整,还利用拟合的一元函数方程对原始数据进行了光滑优化处理,达到了较好的滤波效果。
4 结束语
通过对常用数字滤波算法进行比较提出了一种基于滤波宽度动态调节的递推中值与基底特征外延算法,提高了滤波效果。主要创新点为:将递推算法与中值滤波算法结合,保证了滤波效果的精确性并且使得信号曲线更加光滑;对递推队列长度进行了讨论和分析,针对含有重要信息的峰顶和峰谷区域动态地调整递推队列长度,还原并保留了数据特征;在数据边界处,针对递推中值算法数据缺失的问题,提出使用最小二乘法对原始数据基底特征进行拟合,根据基底特征对缺失数据进行预测和补充。为了实现更加精确的滤波效果,还需对不同数据进行滤波实验并且对代码进行优化,后续将进一步深化研究。
