微环谐振腔中点光源产生轨道角动量的特性
2022-02-25陈波刘进
陈波, 刘进
(1中山大学光电材料与技术国家重点实验室,广东 广州 510275;2中山大学物理学院,广东 广州 510275)
0 引言
量子光源作为量子信息处理的关键器件之一,是量子计算、量子通信、量子模拟等应用的基础。实验上可以在不同的原子或者类原子二能级系统中观测到单光子发射,比如囚禁原子、离子[1,2]、金刚石色心[3]、半导体量子点[4,5]、单原子层的二维材料[6]等系统。这些具有二能级或者等效二能级系统的量子系统可以近似等效为点光源辐射子,辐射的光子以4π角向空间辐射。由于点光源是一个发散的系统,实验上对光子的收集效率很低,光的传播方向性也很差。为了解决点光源发光自身收集效率低、方向性差的问题,实验上可以利用微腔等结构把点光源辐射的光耦合到微腔的固定模式中,以实现对光的高效率收集和调控。以半导体量子点固态量子光源为例,比如可以结合微盘腔[7]、光子晶体微腔[8]、微柱腔[9]等微腔结构,利用腔量子电动力学效应提高量子点的发光特性,制备在芯片上可拓展集成的量子器件。因此,基于微腔的量子光源调控研究是量子信息技术发展的重要研究方向之一。
另一方面,提升量子信息编码的容量也是量子信息技术发展过程中面临的重大挑战之一。光子的轨道角动量(OAM)作为希尔伯特空间无限维完备的正交解,理论上可以进行无限维度的编码,可以极大地提高信息处理的容量,是高维量子信息处理的重要资源。2001年,奥地利的Zeilinger小组利用BBO晶体的自发参量下转换制备出了光子的轨道角动量纠缠态[10];之后,他们通过干涉法将偏振纠缠转移到OAM中,产生并验证了光子的高维轨道角动量纠缠[11]。2016年,他们实现了10010量子数的量子纠缠态[12]。在国内,郭光灿院士领导的研究团队利用光子的轨道角动量进行了一系列开创性的工作。2007年,张沛等研究人员利用光子的轨道角动量演示了量子随机行走[13]。之后,史保森研究小组实现了OAM单光子、OAM纠缠光子以及OAM与偏振组成的混合纠缠光子的频率转换[14],证明了在频率变换过程中单光子的量子相干性和光子对的纠缠特性保持不变[15]。这些工作对实现不同波长的OAM量子网络的对接和量子信息交互具有重要意义。
在产生轨道角动量量子态的研究方面,前期的研究主要基于晶体材料非线性效应的概率性产生,效率较低,成为制约高维量子信息处理的主要瓶颈。为了克服上述问题,本研究组前期在半导体量子点量子光源的基础上,利用内壁嵌入角向光栅的微环腔实现了携带轨道角动量叠加态的单光子源[16],该工作证明了芯片上集成量子光源产生轨道角动量的可能性。为了进一步了解微环谐振腔中产生轨道角动量的特性,本文在前期研究的基础上完善了微纳尺度下微环谐振腔产生轨道角动量的机理和性质,该研究工作对进一步了解利用微环谐振腔产生轨道角动量量子态有良好的促进作用,也对发展具有更高信息容量和更高安全性的量子信息技术具有重要意义,有助于进一步提升量子光源产生光子的编码信息容量,提高量子通信和量子计算的效率,促进芯片上高维量子通信、量子计算、量子存储等领域的发展。
1 微环谐振腔产生轨道角动量的原理
光在微环谐振腔中传播时,类似于圆盘中的回音壁模式(WGMs),光也会沿着环形波导全内反射传播,由此形成的WGM模式本身可携带高维的OAM态[17]。但是这些腔模携带的轨道角动量都局域在微环腔的内部,很难从空间模式上对其开发利用。2012年,余思远研究小组首次利用在微环内壁嵌入均匀分布的角向光栅[18]把局域在微环腔内的OAM抽取到自由空间,实现了微纳尺度下产生光子轨道角动量,该方法引起了研究者的广泛关注[19,20],也为在芯片上集成产生轨道角动量量子态器件提供了思路。
把二能级系统的量子光源等效成点光源,可以把点光源放置于内壁嵌入角向光栅的微环波导内部,如图1所示,柱坐标系下,(ρ,φ)坐标为环形波导平面,z为轨道角动量模式的中心轴。当光与微环腔腔模耦合之后,光将沿着微环波导顺时针(CW)和逆时针(CCW)传播,形成传播波矢相反的CW和CCW两个模式,这两种反向传播模式会进行干涉叠加,在环形谐振腔中形成驻波模式。当两种模式被角向光栅调制之后,存在于微环内部的模式会以螺旋传播方式被散射到自由空间,从而实现轨道角动量光子的产生。对于具有固定光栅数q的微环谐振腔,其中的WGMs阶数p决定了出射的OAM的拓扑电荷数l,即l=sign(p)(|p|−q)[18]。因此,点光源在该微环腔产生向上辐射的轨道角动量模式是阶数为l的叠加态。
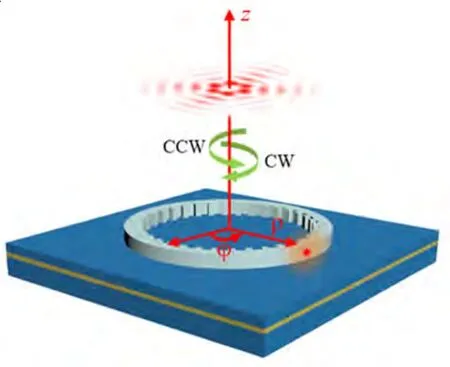
图1 点光源在微环谐振腔中产生轨道角动量叠加态的示意图Fig.1 Schematic diagram of the point light source in the microring resonator for generation of photons carrying superposition states of OAM
设光在微环中沿CCW传播的方向为正方向,在近轴近似条件下,向z方向传播的CCW涡旋光场的远场辐射横向场分量可以表示为[21]
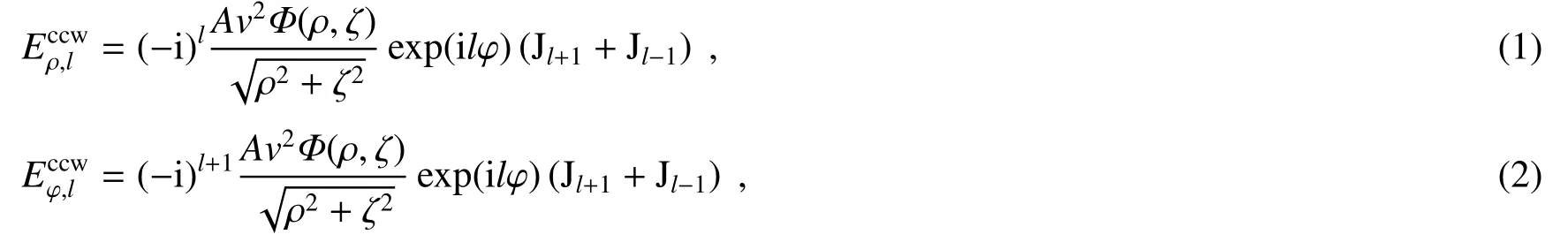
式中:常数A=PAq/(8πε0R3),归一化传播常数 ν=2πR/λ,传播过程中Jn=Jn(νρ/ζ)表示第一类贝塞尔函数。由于环形腔中的CW模式Ecw和CCW模式Eccw的振幅相同,但其拓扑电荷相反,初始相位差为δ(φ),因此向上辐射的轨道角动量模式叠加态可由径向分量和角向分量叠加得到,其总强度分布变为

其表示远场强度分布是随轨道角动量维数变化的驻波模式。
2 点光源在微环谐振腔中的辐射特性
当点光源置于微环谐振腔内,产生OAM的微环谐振腔是圆柱对称的结构,光在谐振腔内产生的模式是麦克斯韦方程的解。为了求解点光源在微环谐振腔中的特性,利用三维有限时域差分(FDTD)方法,使用商业软件LumericalFDTD进行求解。基于实验上使用的GaAs/InAs量子点特性,模拟的波长大约在900 nm附近,与量子点发光峰相对应。将水平极化的电偶极子(等效为点光源)置于微环波导的中心,在厚度为160 nm的GaAs(n=3.5)材料的微环谐振腔的内壁嵌入角向环形光栅,光栅个数为q=92(对应每个波腹处),该微环谐振腔放置在SiO2层(n=1.45)上,上方是空气(n=1)。微环的半径为5µm,环的宽度为300 nm,每个光栅元件从环形波导内壁突出60 nm,宽度为60 nm。
点光源在微环谐振腔内辐射出的光子会受到腔的调制,由于腔量子电动力学效应会改变量子体系的自发辐射速率,因此会使光子的辐射速率加快或者抑制。由于内壁嵌有光栅的微环腔存在较大的散射,微腔与腔内辐射光子的耦合不足以抵消系统的耗散,系统表现为弱耦合体系。如图2所示,是上述参数条件下微环谐振腔对点光源辐射不同维数轨道角动量叠加态光子自发辐射速率的影响,当辐射的光子与微腔模式共振时态密度增加,会增强自发辐射速率;远离微腔共振频率时态密度减小,会抑制自发辐射速率,体现了微腔对点光源调制的珀塞尔(Purcell)效应。在微腔泄漏模等影响下,点光源辐射的光子与腔模发生不完全耦合,定义模式的β因子为耦合进一个腔模的光子数和点光源辐射的总光子数的比值,即[22],式中γc为微腔中的自发辐射速率,γ0为真空中的自发辐射速率,Fp为Purcell因子。如图2中的腔模|+4〉+|−4〉叠加态对应Fp=5.8时,会有约85.3%的光子与腔模耦合并转换成携带轨道角动量的光子。当Purcell越大,点光源辐射的光子耦合进腔模携带轨道角动量的光子也会越多。同时,由于Purcell的提高,可以减弱退相干的影响,从而提高单光子的不可分辨性。
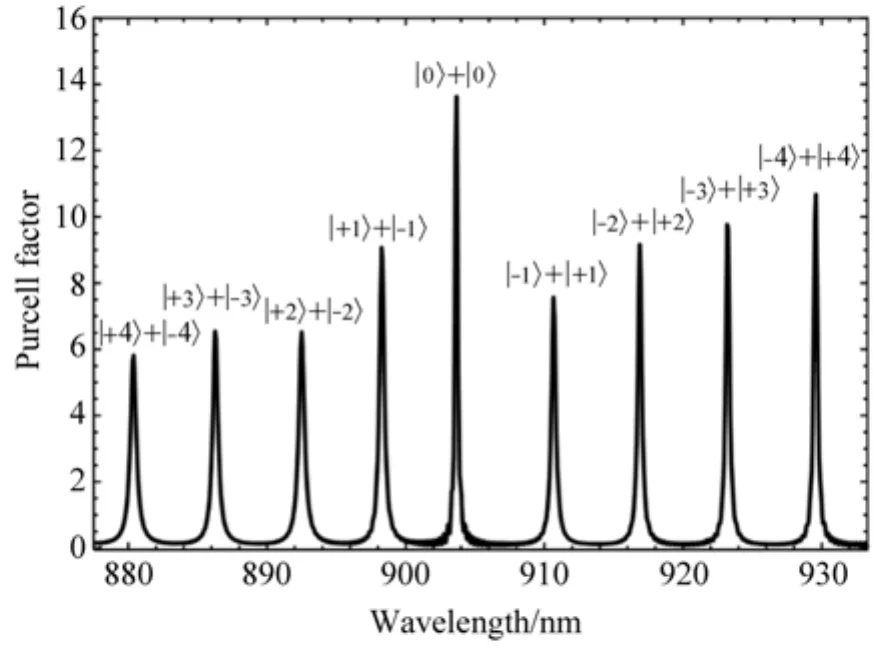
图2 微环谐振腔对点光源自发辐射速率的影响Fig.2 Influence of microring resonator on the spontaneous radiation rate of point light source
当点光源以4π空间角向外辐射时,在单个方向上收集光子的效率低于2%。当点光源在微环谐振腔内,利用微腔可以调制自发辐射和远场模式,从而提高收集效率。基于上述模拟微环谐振腔的参数,利用FDTD Solutions中的探测器收集向上辐射光子的能量,考虑到实验上利用物镜(NA=0.65)进行远场收集,对应的远场方位角约为40◦,对|−3〉+|+3〉和|−4〉+|+4〉叠加态与腔模共振的频率在该方位角内的能量积分与点光源辐射能量的比分别为24.14%和22.64%,说明内壁嵌入角光栅的微环谐振腔向上抽取的轨道角动量光子比点光源4π空间角辐射的光子有较大提升。但是由于角向光栅的散射效应抑制了收集效率的进一步提高,实验上可以在微腔的下面设计反射结构以进一步提高光源向上的收集效率。
由二能级系统简化的点光源(如量子点)在微腔中产生单光子时是一种非经典光源,其行为表现为反聚束[23],服从亚泊松分布。由于单光子不可再分,只能产生或者湮灭,实验上通常用二阶关联函数在零延时的值g(2)(0)来表征单光子的纯度,当g(2)(0)<0.5时,即可认为是单光子源,g(2)(0)的值越接近零,则单光子的纯度越高。当把单光子分成两路进行二阶关联函数测量时,在光子数态表示中,二阶关联函数的表达式为

3 轨道角动量叠加态的特性
3.1 腔模及电场特性
点光源在微环谐振腔中受到腔模和角向光栅的调制,会产生向上辐射携带轨道角动量的光子,基于上面模拟仿真的参数,得到微环谐振腔向上辐射的光谱如图3所示,每个腔模对应不同的OAM叠加态辐射谱,自由光谱范围(FSR)约为6 nm,其中l=0的叠加态腔模位于903.5 nm。由于受光栅散射的影响,微环谐振腔的品质因子Q降低到约1000左右。图3上方从上到下分别对应每个腔模的近场电场分布(距离微环上表面半个波长)、相位分布、远场分布和矢量偏振特性。可以看出带角向光栅的微环谐振腔从腔模出射的OAM态是CW和CCW模式的叠加,这种叠加态可表达为[11]。

图3 点光源在微环谐振腔的辐射谱和产生OAM叠加态的电场分布、相位分布及偏振特性Fig.3 The spectrum of point light source in microring cavity and the electric field distribution,phase distribution and polarization characteristics of the superposition states of OAM
从近场的电场和相位分布,可以看出从微环中心向上辐射的轨道角动量叠加态的模式及量子数信息。在实际应用中常用到的是轨道角动量的远场信息,在远场矢量偏振分析图中把径向矢量偏振(RP)和角向矢量偏振(AP)叠加在一起,从图上可以方便地看出径向和角向偏振对应的空间分布位置。结合远场强度分布和矢量偏振特性,可以看到l=0的远场是一个环形模式场,对应分布在径向矢量偏振的空间位置,是典型的径向偏振矢量涡旋模式。对于l=p−q>0的模式场,远场的强度信息主要分布在径向偏振的位置,角向偏振的强度较弱,可以方便地从远场模式中判断出OAM的阶数。同时,随着|l|的增大,其远场强度分布的轨道环半径增大。对于l=p−q<0的模式场,由于径向偏振和角向偏振的强度几乎相等,而且分布在比较接近的轨道环上,因此模式叠加之后比较复杂,通过矢量偏振信息可知,可以把远场模式投影到径向偏振或者角向偏振基矢进行远场信息处理,从而方便判断出OAM的量子数信息。
在上述分析中假设点光源放置在电场分布的波腹,点光源被微环调制的CW和CCW模式是简并的,因此从辐射谱上看到的模式都在同一个频率上叠加。而在实验过程中会出现点光源放置在不同位置处,如图4(a)所示,当点光源放置在电场模式的不同位置处,其远场模式会有相应的变化。比如对于轨道角动量|+3〉+|−3〉的叠加态,当点光源位于波腹和波节的位置处(如位置1和3),产生的CW和CCW模式均是简并的,其远场模式会有π的相位差。而对于不是波腹和波节的位置处(如位置2和4),点光源在微环谐振腔中产生的CW和CCW模式将不再简并,因此在微环腔发辐射谱中可以看到在l=0处会出现谱线的劈裂,如图4(b)所示。劈裂的模式中,如插图所示,位于903.5 nm的模式(腔模1)是径向矢量偏振模式,位于905 nm的模式(腔模2)是角向矢量偏振模式。
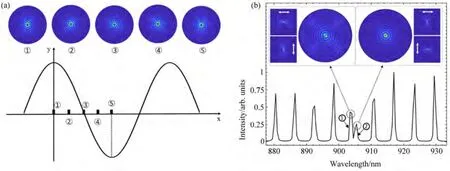
图4 点光源在微环谐振腔中不同位置处产生OAM叠加态的特性。(a)点光源在微环谐振腔中产生|+3〉+|−3〉叠加态所对应点的位置及远场分布;(b)点光源辐射谱中l=0谱线劈裂对应的远场分布Fig.4 Properties of the superposition states of OAM with the point light source at different positions in the microring.(a)The far field distribution of the superposition state with|+3〉+|−3〉for the point light source at different positions in the microring;(b)The far field distribution corresponding to the state l=0 with the splitting spectrum for the point light source in the microring
3.2 轨道角动量模式的纯度特性
对于高维OAM态的表征,除了描述其维度信息,每个轨道角动量态的纯度是模式利用过程中重要的因素之一。从上面的分析可知,微环谐振腔向上辐射产生的轨道角动量是有径向矢量偏振或者角向矢量偏振特性的,要对其模式的纯度进行分析,可以把径向模式和角向模式投影到圆偏振基矢
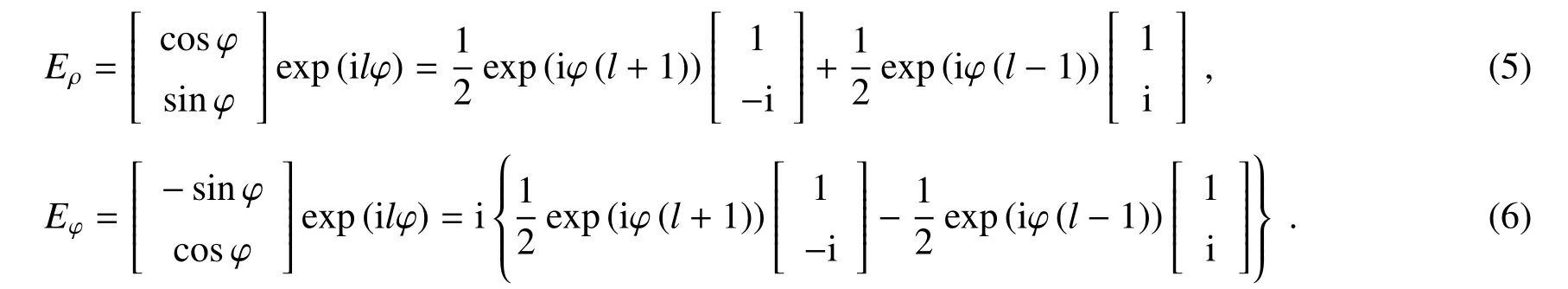
由此可知,在右旋圆偏振基矢中轨道角动量模式为l+1阶,而在左旋圆偏振基矢中轨道角动量模式为l−1阶。在得到分解后的轨道角动量模式之后,利用反向涡旋相位对其进行解调,可以得到中心为高斯模式的亮斑,从而得到轨道角动量的维度信息,并分析纯度信息。
如图5所示,把l=−4到l=+4的腔模叠加态投影到左旋圆偏振基矢中,并利用l′=−4到l′=+6的反向螺旋相位进行解调,可以看到每一行l=−(l′−1)阶模式的中心均出现了高斯模式的亮斑,比如对于轨道角动量|+3〉+|−3〉的叠加态,在使用反向涡旋相位l′=−2到l′=+4时模式中心出现了亮的高斯光斑,与(5)、(6)式中描述的轨道角动量维数信息一致。

图5 OAM叠加态投影到左旋圆偏振基矢解调的模式分布Fig.5 Simulated far-field patterns projected to the left-hand circularly polarized basis for the emitted photons in an angular momentum superposition state
为了进一步验证这种微环谐振腔调制出射的OAM叠加态模式的纯度性质,利用上面反向涡旋相位解调得到的模式,通过计算中心为高斯亮斑的OAM模式在整个OAM谱中的占比,可以得到不同叠加态中各分量的纯度信息,如图6所示,各叠加态的纯度之和均大于90%。在l=0时,投影到左旋圆偏振基矢之后,用l′=+1解调后得到其纯度约为92%。通过对点光源在微环谐振腔中产生轨道角动量叠加态的定量分析,有助于更好地理解芯片上集成微环谐振腔产生轨道角动量的纯度性质,也为实验和实际应用提供了有效方法。
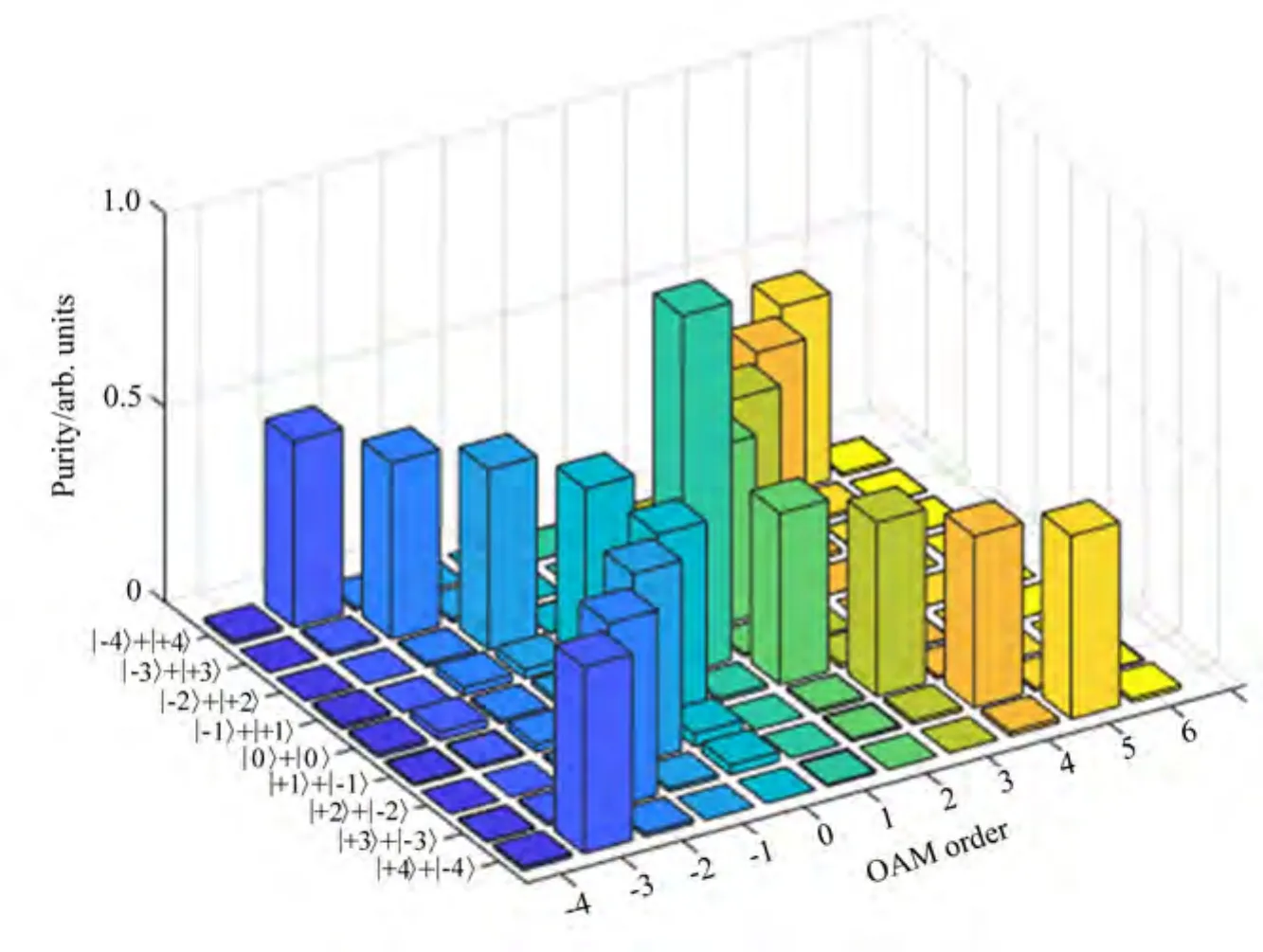
图6 辐射光子携带OAM叠加态的纯度特性分布Fig.6 Simulated OAM purity distributions of the emitted photons in an angular momentum superposition state
4 结论
高维轨道角动量叠加态是量子信息系统中非常有用的光子态,结合芯片上可集成的固态二能级量子光源,本研究利用微环谐振腔对量子光源进行调控并产生轨道角动量量子叠加态,该方案具有器件尺寸小、可集成、可扩展的优势。对点光源在微环谐振腔中的辐射特性及产生轨道角动量叠加态的近场和远场特性进行了分析,通过对轨道角动量远场叠加态的偏振分析及远场模式纯度的定量分析,为集成轨道角动量光量子器件的发展提供了有效方法,有助于推进量子光源性能的按需调控和高维量子信息处理技术的发展。
