基于光取向液晶叉型光栅的涡旋光产生器

王华才,曹瀚,于宏冠,陈鹏,胡伟

(南京大学现代工程与应用科学学院,江苏 南京 210093)

0 引言

近三十年来,相位型涡旋光场(OV)引发了光学界持续广泛的关注。其相前绕传播轴呈螺旋扭曲分布,一个波长范围内相前的扭曲次数被定义为拓扑荷m。为了保持传播过程中的相位连续性,m要取整数,这意味着轨道角动量(OAM)是量子化的。m可以取任意整数,其符号表示相位扭曲的方向[1]。m作为OAM中的一种重要特性,在光通讯、微操控、光学成像、量子信息及精密测量等领域带来了全新的应用[1,2]。

涡旋光场的产生与调制在上述应用中处于首要位置,目前已开发出一系列的方法,如:模式变换法[3,4]、直接相位重构法[5−7]、q板调制等[8−10],然而这些方法仅适用于对特定波长的固定模式转换。另一种就是本文要重点论述的叉型光栅(FG)调制法[11,12]。早期基于图案化电极[13]和聚合物分散液晶[14]制备的叉型光栅,其固定的形状导致输出涡旋光的拓扑荷无法改变。空间光调制器(SLM)可以实现全息图的动态刷新,但仍存在像素尺寸大、转化效率低、驱动复杂等不足[15]。

本文介绍了一种基于数字微镜阵(DMD)动态掩模缩微投影偏振曝光的液晶图形化配向技术[17],实现了液晶叉型光栅、达曼叉形光栅、具有螺旋结构的达曼叉形光栅的制备,并介绍了其在涡旋光场产生及其阵列化和宽带OAM光场产生方面的应用。

1 研究进展

DMD芯片会根据计算机生成的掩膜图案单独控制每个反射镜的倾斜角度,对光束进行整形,形成微图案[16]。这一特性使DMD可以作为一个能够生成各种复杂图案的动态掩膜板。由于切换掩膜时不会发生移动,多步曝光时对准精度极高,并且投影透镜能够避免光束扩散的问题,因此具有高分辨率。将DMD产生的微图案经过偏振片后投射并记录到磺酸偶氮染料(SD1)薄膜上,充分结合DMD的图像生成能力、SD1的可擦写性以及偏振片的精密转角控制,可实现对液晶方位角的点对点任意操控[17]。

1.1 叉型光栅产生涡旋光

叉型光栅是将涡旋光[相位Ψ1=exp(imθ)]与平面波[相位Ψ2=exp(ikx)]相干的结果[18],其计算全息可描述为[9]

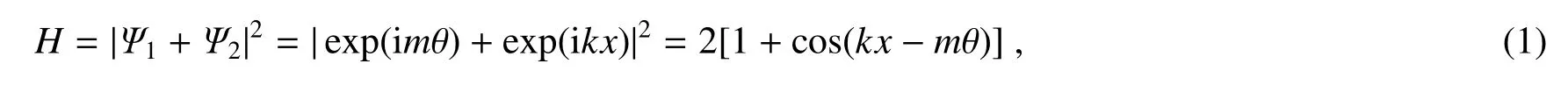
式中θ=tan−1(y/x)是柱坐标系的极角,k是平面波波矢。当全息图被一束高斯光ΨG=exp(−r2/w2)照射时,远场夫琅禾费衍射的光强分布为高斯光ΨG与全息函数H乘积的傅里叶变换[9],即

对计算全息图进行二值化处理,则所对应的衍射级次n携带mnOAM的涡旋光,且各级能量分布与传统二值光栅一致。

将m=1的二值全息图[图1(a)]通过光取向技术写入液晶盒形成正交的平行取向区域,得到液晶叉型光栅[图1(b)]。当高斯光正入射该叉型光栅时,其衍射图样[图1(c)]显示0级为高斯光,其余衍射级(±1∼±4)为与拓扑荷对应的涡旋光,其强度分布随级次升高显著降低。

液晶能够直接对相位进行调制,因此可以跳过全息图直接利用相位叠加来进行设计。除二值化相位控制,液晶光取向同样适用于连续相位变化。几何相位又称PB相位[19],源于光的自旋轨道相互作用,带来自旋(圆偏振)相关的光束分离现象,即光子的自旋霍尔效应[20]。几何相位与光的偏振演化过程相关,对映到庞加莱球两点之间,不同路径引入的相位有差别,其大小等于这两条路径所组成的庞加莱球上的一闭合曲面所对应的立体角的一半[21]。偏振演化过程只依赖于光轴方向这一几何特征,通常几何相位元件都是基于半波条件实现的,通过光取向控制液晶指向矢(光轴)空间分布即可进行特定相位调制以产生目标光场。几何相位差等于相应光轴角度差的2倍,其符号取决于入射圆偏振。

(1)式中的叠加相位可以转化为[22]右边第一项描绘了q=m/2的q-plate的相位,ϕ(x,y)=arctan(y/x)是x-y平面内的方位角;第二项描绘了周期为Λ的偏振光栅的相位。当高斯光入射时,其出射相位可由琼斯矩阵计算。计算得出该类偏振叉型光栅只存在3个衍射级,即携带相反拓扑荷的±1级以及与入射光相同的零级。半波条件下,不同圆偏振分量通过样品后发生圆偏振反转,并加载上共轭的几何相位[图1(d)]。改变入射偏振,可以调谐能量在相反OAM涡旋光间的分配[图1(e)][22]。对于基于图案化电极的叉型光栅,其±1级最大衍射效率约为27%[13];对于基于聚合物液晶的叉型光栅,其衍射效率更低,约为13%∼17%[14];而基于光取向技术的液晶叉型光栅的±1级衍射效率通过外加电场可以达到约99%,远高于上述两者,接近理论极限。此外,前两者由于固定的形状导致输出涡旋光的拓扑荷无法改变,而后者可以刷新全息图,改变输出拓扑荷。

通过观察三种偏振光栅的衍射图样可以发现:对于m=2的偏振叉型光栅,其环形衍射图样具有连续性,图像边缘犀利,强度均匀;对于m=2.5的偏振叉型光栅,其分数部分引起液晶角向指向矢有π/2的移动,导致环形衍射图像断裂;对于m=1、p=1的偏振叉型光栅,由于p=1会引起液晶径向指向矢的有π/2的移动,导致径向相位移动π,产生径向不连续的衍射图像。由实验结果可以看出,除了m=2的偏振叉型光栅,m=2.5[图1(f)]和m=1、p=1[图1(g)]的偏振叉型光栅同样可以实现类似功能,实验结果与理论分析一致。

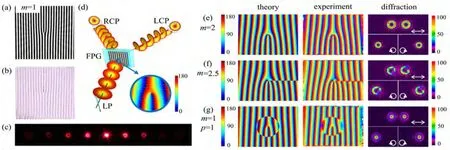
图1 (a)m=1的二值全息图;(b)m=1的二值液晶叉型光栅显微图;(c)对应(b)的衍射图像[18];(d)液晶偏振叉型光栅衍射示意图,含有携带不同拓扑荷与径向指数(e)m=2,(f)m=2.5,(g)m=1,p=1液晶偏振叉型光栅的理论与实测光轴分布及对应的不同入射偏振时的衍射图像[22]Fig.1 (a)Binary computer-generated hologram with m=1;(b)Micrograph of a LC fork grating of m=1;(c)The diffraction pattern of(b)[18];(d)Scheme of the diffraction of a LC polarization fork grating.Images of theoretical and experimental optical axis distribution,and polarization dependent diffractions of LC polarization fork gratings with topological charges and radial index of(e)m=2,(f)m=2.5,(g)m=1,p=1[22]

1.2 达曼叉型光栅产生阵列化的涡旋光

二值化叉型光栅一个周期只有两种相位分布,两种相位比例1:1时效率最高且高阶级次效率较低。偏振叉型光栅虽然高效,但无法同时产生一系列OAM的涡旋光阵列。达曼光栅同样是二值相位(0,π)光栅[23],其在一个周期内引入多个相位转变点,通过优化其数量和位置即可实现系列目标级次等能量的衍射图样[24,25]。达曼光栅的相位分割原理亦可拓展到叉形光栅。

图2(a)展示了一个二维达曼叉型光栅(DVG)[26]的相位图。对于二维达曼叉型光栅,其涡旋光阵列的拓扑荷分布满足nxmx+nymy,其中nx、ny分别表示x、y方向的衍射级次,mx、my分别表示x、y方向的拓扑荷。图2(b)显示了一个mx=1、my=1的5×5正交平行取向的达曼叉型光栅的显微图。当高斯光入射该样品时,可以获得等能量分布的涡旋光阵列,OAM取值为±1∼±4,斜135◦每一行具有相同m。在外加2.5 V电场时,测得衍射效率约为74%,显著高于基于空间光调制器生成的涡旋光栅[27]。调节外加电场可以在宽波段范围内匹配不同波长的半波延迟条件,实现从可见光到近红外的高效OAM光束阵列生成[图2(c)]。图2(d)、(e)分别给出了632.8 nm、532 nm激光入射时的衍射图样。可以看出不同衍射级的能量分布略有差异,存在一些强度失真,这是由于光栅的不完美结构或者相位奇异性[28]引起的,可以归因于制造过程中引入的误差。这些问题可以通过提高曝光分辨率来进一步解决。实验中所使用的E7液晶响应时间为毫秒级,若替换为双频[29]或铁电液晶[30],响应时间将进一步提升到亚毫秒甚至十微秒量级。此处仅以5×5的达曼叉型光栅为例。实际上,通过合理地选择相位转变点可以自由设计达曼叉型光栅的衍射级次阵列。

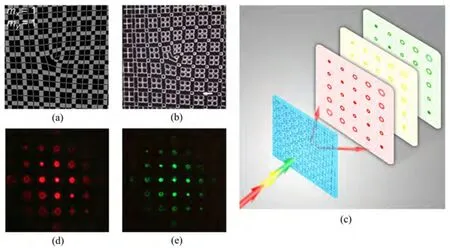
图2 (a)mx=1,my=1的5×5达曼叉形光栅的相位图;(b)液晶达曼叉形光栅的显微图像;(c)电调样品产生不同波长OAM阵列的示意图;(d)632.8 nm,(e)532 nm入射波长的衍射图像[26]Fig.2 (a)A phase diagram of a 5×5 DVG with mx=1,my=1;(b)Micrograph of the LC DVG;(c)The OAM array of different wavelengths generated by an electrically tunable DVG;Diffraction patterns at(d)632.8 nm and(e)532 nm,respectively[26]

1.3 螺旋结构产生宽带涡旋光

达曼叉型光栅虽然可以针对不同波长,通过加电调节进行效率优化,但是无法同时满足宽带高效模式转化的需求。胆甾相液晶(CLC)是一维手性光子晶体,呈现空间周期性螺旋结构,其表现出圆偏振选择的布拉格反射带可以表示为∆λ=(ne−no)p=∆np,其中p表示CLC螺距[31,32],在整个反射带内反射率相等。用胆甾相液晶替换前述达曼叉型光栅中的向列相液晶,当波长位于布拉格带内的入射光沿螺旋轴正入射时,与CLC液晶旋性相同的圆偏光分量将被反射并发生相位转换,衍射为携带拓扑荷nxmx+nymy的等能量涡旋光阵列,其变换函数为[33]

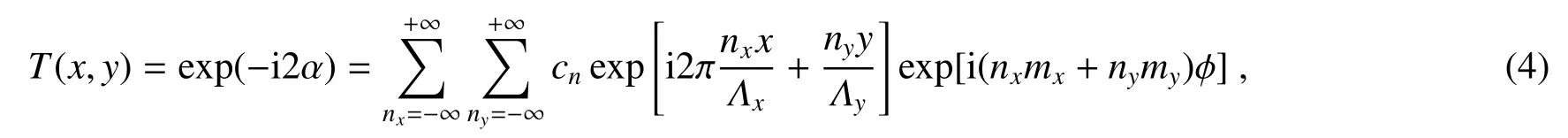
式中:α是液晶指向矢,Λx、Λy分别表示x、y方向的光栅周期,ϕ表示x-y平面内的方位角,|Cn|2是(nx,ny)衍射级的衍射效率。与液晶旋性相反的圆偏振分量只发生了均一的相移而无额外的相位加载,被直接透射。

本课题组设计了mx=1、my=3的2×5达曼叉型光栅[图3(a)],灌入胆甾相液晶后受表面锚定诱导生成螺旋结构,螺旋轴沿z轴方向,且不同区域的起始和终态的取向方向不同(0◦和90◦)[图3(b)]。偏光显微镜下的取向边界结构[图3(c)]与设定的相位分布图[图3(a)]完全吻合。采用了大双折射率母体液晶,合理调节手性剂掺杂量,使得布拉格反射带跨越了525∼641 nm这一波段[图3(d)]。利用该螺旋结构达曼叉型光栅,实现了116 nm范围内多个波长涡旋光束阵列的同时高效转换[图3(e)],预设级次间能量具有很好的均一性[图3(f)],总反射衍射效率达到约55%[34]。

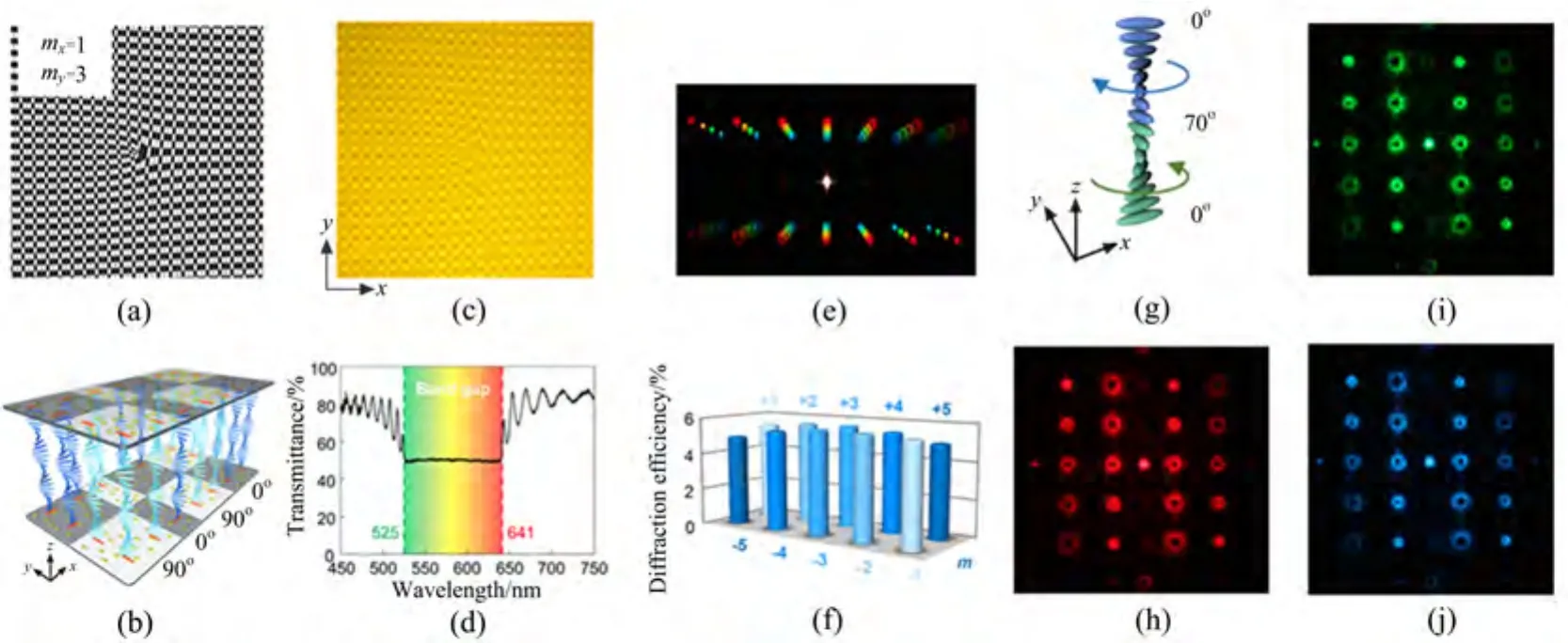
图3 (a)mx=1,my=3的2×5达曼叉型光栅;(b)局部液晶指向矢分布示意图;(c)达曼叉型光栅的显微图;(d)布拉格反射带;(e)多个波长同时产生的涡旋光阵列;(f)不同级次的衍射能量分布;(g)双层反向扭曲螺旋结构;(h)632 nm,(i)532 nm,(j)480 nm的衍射图样[34]Fig.3 (a)A 2×5 DVG with mx=1,my=3;(b)Scheme of local director distribution;(c)Micrograph of the DVG;(d)Bragg reflection band;(e)Multi-wavelength OV arrays;(f)Diffraction efficiencies of different orders;(g)Scheme of the dual-twist structure;The diffraction patterns at(h)632 nm,(i)532 nm,(j)480 nm,respectively[34]

除了上述反射型几何相位元件,在透射型达曼叉型光栅中同样可以通过引入双层反向扭曲螺旋结构来实现宽波段高效率的几何相位调制。通过分步旋涂掺杂相反手性剂的液晶聚合物前体并光照聚合来实现双层反向扭曲螺旋结构[图3(g)],并优化手性剂掺杂浓度和旋涂条件使得底层右旋70◦,上层左旋70◦,以达到整个可见光范围内的宽波段色散补偿。利用该材料体系和工艺制备了mx=3、my=1的2×5液晶达曼叉型光栅,并展示了不同波长下高效的涡旋光阵列的产生[图3(h)∼(j)]。双层反向扭曲螺旋结构的引入,很好地解决了平行取向几何相位光学元件在入射波长偏离半波条件时衍射效率明显下降这一限制,对宽波段高效透射型几何相位元件,尤其是在液晶聚合物柔性平面光子学元件领域具有非常重要的意义[33]。

2 总结与展望

液晶光子学作为现代光子学的重要组成部分,正朝着小型化、集成化、多功能和自适应等方向发展。液晶兼具液体的流动性和晶体的各向异性,光取向技术使得液晶方位角的灵活操控成为可能,可实现对光波前的点对点操纵,包括任意、可重构的涡旋光的生成、调制和检测。基于液晶光取向的光场调控技术大大增强了光束整形能力[35,36],并拓宽了衍射光学的应用前景。这里仅以各类叉形光栅为例展示了该技术涡旋光光场产生方面的具体应用,该技术在经典光学到量子信息等广阔的领域都具有巨大的潜力[37]。目前仍旧面临一些急需解决的问题,例如:复杂液晶组装结构的精准构建,结构关联性质的多元外场调控规律,以及特殊波长下的液晶响应性等都尚待进一步研究。相信伴随着相关领域研究的不断深入和系统化、技术的不断发展和完善、液晶光子学在理论和技术上的持续创新,有望推动光子学的进一步发展并开拓出全新的甚至是变革性的应用。