基于空间阵列式惯性单元的防冲钻孔机器人位姿解算方法

王忠宾，司 垒，王 浩，张修峰，赵世豪，魏 东，谭 超，闫海峰

(1. 中国矿业大学 机电工程学院，江苏 徐州 221116； 2. 山东能源集团有限公司，山东 济南 250014)

随着我国煤矿开采深度和强度的不断加大，冲击地压已成为我国深部煤矿开采中最严重的动力灾害之一，其发生频次和破坏强度不断增大，对深部煤层的安全开采造成了极大的影响。目前，我国煤矿企业进行冲击地压钻孔卸压作业时，卸压作业需要人员进入危险区域，卸压过程中容易诱发冲击地压灾害，进而造成较大的人员伤害事故。因此，迫切需要实现钻孔卸压作业的机器人化，而钻孔卸压区域的机器人化作业首要解决的关键技术便是钻孔机器人的精确定位和定姿问题。

现有的移动机器人定位技术主要包括红外定位、超宽带定位、超声波定位、里程计定位、视觉定位、激光雷达定位及惯性导航定位等。JOBES等提出了一种采煤机的远程定位系统MPHS，并给出了计算位置和航向的方法。MARREF和BARRET基于超声波技术实现了移动机器人在自主导航过程中的路径规划及合理避障。LEDERGERBER A等利用单向信号传递的超宽带雷达开发了一种定位系统，通过在固定位置设置收发器，获取目标位置信息，以达到定位目的。冯佳萌等提出了一种增加扫描匹配(SM)和离散傅里叶变换(DFT)的优化AMCL算法，实验结果表明机器人运动过程中轴绝对定位精度误差减小为0.020 m，轴绝对定位精度误差减小为0.019 m。徐庆坤等提出了一种基于UWB与里程计融合的移动机器人定位方法，其平均定位误差为0.2 m。朱道俊等设计了基于视觉和轮速计紧耦合的轮式机器人定位算法，算法轨迹估计误差在0.5%以内。尚磊等基于开源ORB-SLAM2算法实现了煤矿井下搜救机器人的精确定位。蔡李花等基于航迹推算的自主定位方法提出了一种有限记忆卡尔曼滤波方法，并采用逐级滤波的方式融合多传感器信息，经过仿真分析，该方法可以稳定实现0.5 m的跟踪精度，提高了矿井救灾机器人的自主定位精度。

煤矿井下巷道空间狭小、环境复杂、工况恶劣，地面上常用的卫星导航定位、无线通讯定位等常规定位技术无法实现在狭长巷道中对钻孔机器人进行精确定位。由于惯性测量单元(IMU)不需要借助外界的信息，用于解算的初始数据来自元件自身，对外界环境依赖小，且不易受到外界环境干扰，也不需要与外接设备交换信息，可以较好的适应井下复杂环境。因此，惯性导航逐渐成为井下移动装备自主导航的重要技术，国内外学者针对基于惯性导航系统的井下移动装备定位方法进行了大量的研究。澳大利亚联邦科学与工业研究组织(CSIRO)推出了基于陀螺仪导向定位的自动化采煤方法(简称LASC)，解决了惯性导航系统与采煤机高度通信、采煤机初始校准、截割曲线生成和支架推移精确推溜控制等难题。赵靖、郭晓晶等提出了基于卡尔曼滤波算法的采煤机惯性导航定位方法，经过卡尔曼滤波不断修正系统设定状态参数与实际状态参数之间的误差，实现对采煤机的精确定位。樊启高、杨海等设计了基于捷联惯导的采煤机定位系统，通过解算采煤机的三轴加速度和三轴角速度来获得采煤机的位姿信息。张羽飞等通过将惯性导航数据与视觉数据进行融合优化求解机器人自身位姿信息，绝对误差由0.6 m降低到0.4 m以下，平均误差由0.20 m减小到0.15 m，均方根误差由0.24 m减小到0.18 m。温良等设计了基于惯性传感器和和超声波融合的导航方法，经过仿真分析后算法输出轨迹的误差在-3～4 cm，满足了煤矿救灾机器人的定位需求。张璞针对煤矿井下巷道道路弯曲、能见度低等问题，提出了一种基于捷联惯导和里程计组合定位的井下移动机器人的定位方法，并利用卡尔曼滤波算法完成对机器人的位姿估计，实验结果表明机器人整体定位准确度达到95%左右，组合定位方法具有可行性。李猛钢针对井下特殊的工作环境，提出了一种基于雷达、IMU和UWB融合的LIU-SLAM方法，大场景下静态绝对定位精度均值10 cm以内，动态绝对定位精度均值25 cm以内，提高了钻孔机器人的定位精度。

尽管国内外学者对移动机器人定位进行了大量的研究工作，但仍然存在一些问题：① 传统的红外定位、超声波定位等移动机器人定位技术，在煤矿井下应用时对实际工况与环境因素的依赖度较高，无法较好地适应实际工作环境；② 惯性导航系统容易随时间产生累积误差，目前针对惯性导航系统累积误差修正的方法主要集中在改进惯性导航算法和利用辅助定位手段校正惯性导航误差方面，缺少从惯性系统结构上抑制累积误差的方法。

为了降低防冲钻孔机器人惯性导航定位带来的累计误差，笔者分析了惯性导航定位过程中产生的确定性漂移与非确定性漂移，建立了空间阵列式惯性单元组件，实现了钻孔机器人位置和姿态的精确解算，并通过仿真和实验验证了所提位姿解算方法的可行性和实用性。

1 空间阵列式惯性单元数据融合模型建立

1.1 坐标系建立及转换过程

基于空间阵列式惯性单元的防冲钻孔机器人位姿解算思想是将惯性单元组件固连在防冲钻孔机器人上，分别测量出其三轴加速度和三轴角速度信息，通过工控机将采集到的传感信息进行解算，获取防冲钻孔机器人的位姿信息。坐标系建立方式如图1所示。

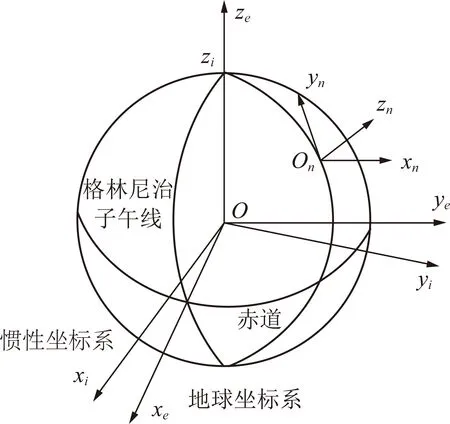
图1 坐标系建立Fig.1 Establishment of the coordinate system

惯性坐标系用表示，原点位于地球中心，轴位于赤道平面内，轴沿着地球的极轴，轴与轴和轴构成右手螺旋。地球坐标系与地球固连，随地球的转动而转动，并用表示，原点位于地球中心，轴指向赤道与格林尼子午线的交点，轴与惯性坐标系重合，轴由右手螺旋定则确定。导航坐标系用表示，用来进行防冲钻孔机器人的定位误差分析。载体坐标系固连在防冲钻孔机器人机身，原点位于防冲钻孔机器人中心处，轴指向前进的方向，轴垂直于机身指向右，轴垂直机身平面指向上。

防冲钻孔机器人的位姿参数在导航坐标系下获得，而惯性单元组件感知的运动特征是相对于载体坐标系的。因此需要建立旋转矩阵实现坐标系的转换。各个坐标系的转换是通过坐标轴的旋转来完成的，步骤如下：导航坐标绕轴转动角度，获得坐标系；之后将获得的坐标系绕其轴转动角度，最后将新坐标系绕其轴转动角度，将导航坐标系转换成载体坐标系，其中为航偏角，为横滚角，为俯仰角。

1.2 空间阵列式惯性单元的布局方法

采用惯性单元对防冲钻孔机器人进行定位、定姿时，由于温度、安装位置和振动等外界因素的干扰，导致惯性单元测量的运动参数与真实运动参数之间存在偏差，使得经过解算之后获得的位姿信息有较大误差。笔者将惯性单元产生的误差分为2类：确定性误差和非确定性误差。确定性误差指的是方向和大小确定的误差；非确定性误差指的是方向或大小不确定的误差。为了尽量消除确定性误差和减少非确定性误差，笔者设计了一种基于空间阵列式惯性单元组件的误差补偿方法，该补偿方法将5个惯性传感单元进行空间阵列式分布，利用空间阵列式惯性单元组件进行数据融合，融合后的传感数据再经过解算，得到防冲钻孔机器人准确的位置和姿态信息。空间阵列式惯性单元的布局方式如图2所示。

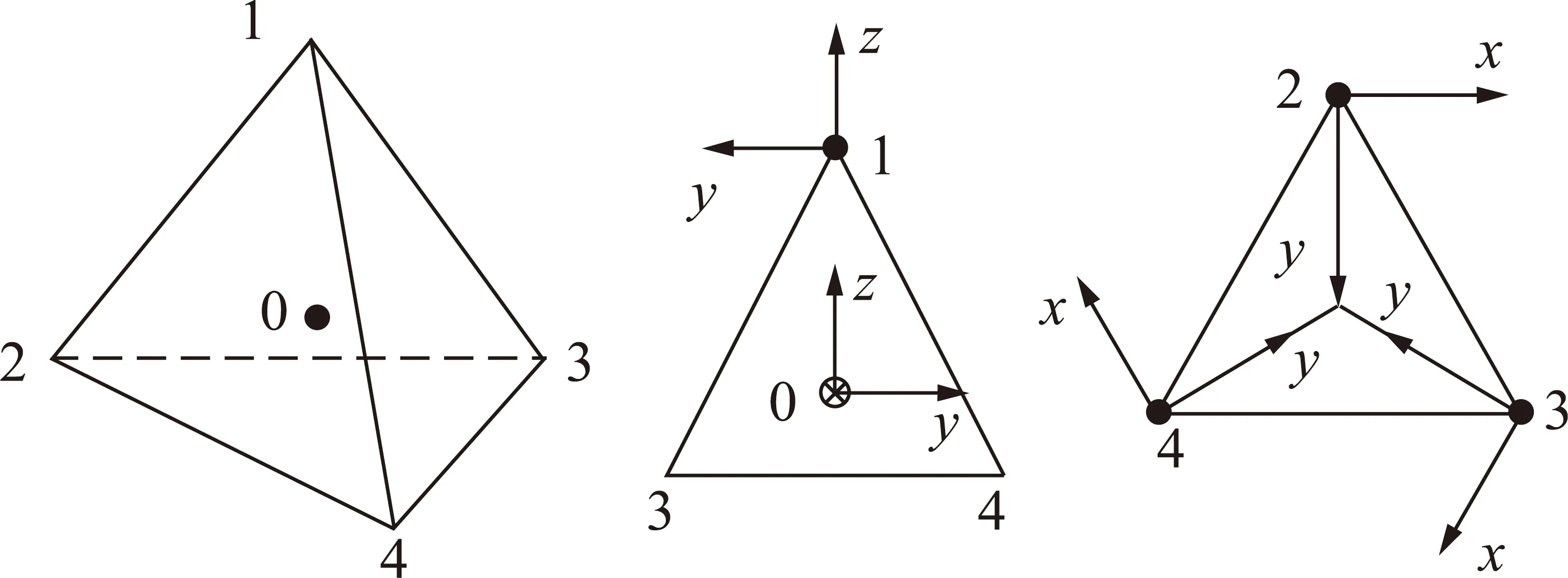
图2 空间阵列式惯性单元布局方式Fig.2 Space array inertial sensing component layout

由图2可知，5个惯性单元分别位于正四面体的4个顶点和中心处，构成了空间布局方式。通过坐标轴的反向布局及坐标轴之间成一定角度的空间结构，对输出参数进行分解和多个传感轴取平均的方法融合5个惯性传感单元数据。理论上，空间阵列式惯性单元能够基本消除确定性误差，降低非确定性误差。

1.3 数据融合方程

..角速度融合方程

当单个惯性单元绕轴转动时，惯性单元输出的角速度包括真实角速度、角速度确定性误差、角速度非确定性误差的矢量和，计算公式为

=++

(1)

由于角速度确定性误差的大小和方向一致，因此在各惯性单元的融合过程中可以将其抵消。对于角速度非确定性误差，如图2所示，3号和4号惯性单元的轴和轴与载体坐标系存在一定角度，融合前需要将角速度换算到载体坐标系坐标轴上。将3号惯性单元测得角速度转换到载体坐标系中需要将坐标系绕轴顺时针旋转150°，由此得到3号惯性单元测得的载体坐标系下三轴角速度为

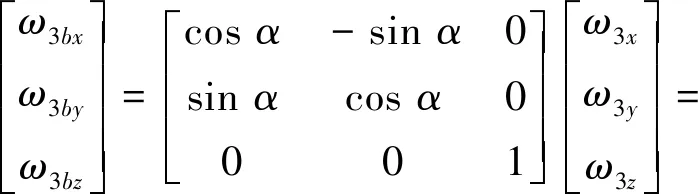
(2)

式中，3，3,3分别为3号惯性单元坐标系变换到载体坐标系绕，,轴旋转的角速度;3,3,3分别为3号惯性单元测量的,,轴旋转角速度；为正三角形的内角，空间阵列式布局(如图2所示)中2号惯性单元、3号惯性单元、4号惯性单元在同一平面上且距离相同构成正三角形。同理，可以得到4号惯性单元测得载体坐标系下的三轴角速度为

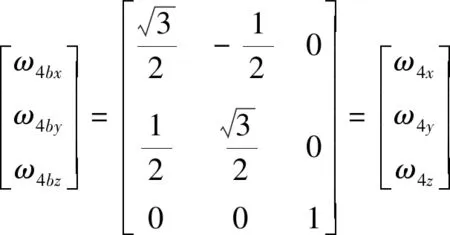
(3)

由此，可以得到的空间阵列式惯性单元组件的角速度融合方程为

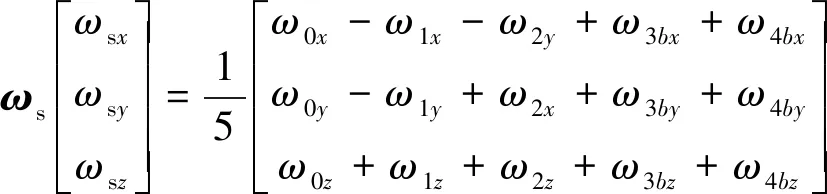
(4)

式中，为空间阵列式惯性单元输出的角速度矢量；s,s,s为绕,,轴旋转的角速度。

通过对式(4)分析可知，惯性单元的确定性误差大小和方向均已知。当阵列式惯性单元中每个惯性单元的确定性误差大小和方向全都一致时，融合后的确定性误差在轴和轴的角速度和比力加速度确定性误差为原来的1/5，轴的角速度和比力加速度确定性误差与单个惯性单元保持一致。虽然实际情况中很难保证多个惯性单元的确定性误差大小和方向都一致，这种情况下融合后的确定性误差仍保持在一个较低的水平，在位姿解算时可以通过误差校准将该确定性误差彻底消除。因此，确定性误差可以被基本抵消，而非确定性误差大小和方向均未知，融合后的非确定性误差可以使每一时刻非确定性误差都保持在较低的水平，并且一些特殊时间点非确定性误差为0，从而抑制误差的快速积累。因此，非确定性误差仅能得到一定的抑制，无法彻底消除。

..比力加速度融合方程

当单个惯性单元出现位移时，其测出的比力加速度包括真实比力加速度、比力加速度确定性漂移和比力加速度非确定性漂移，计算公式为

=++

(5)

由于比力加速度为矢量，可以在空间内进行合成和分解，所以空间阵列式惯性单元的比力加速度融合方程为

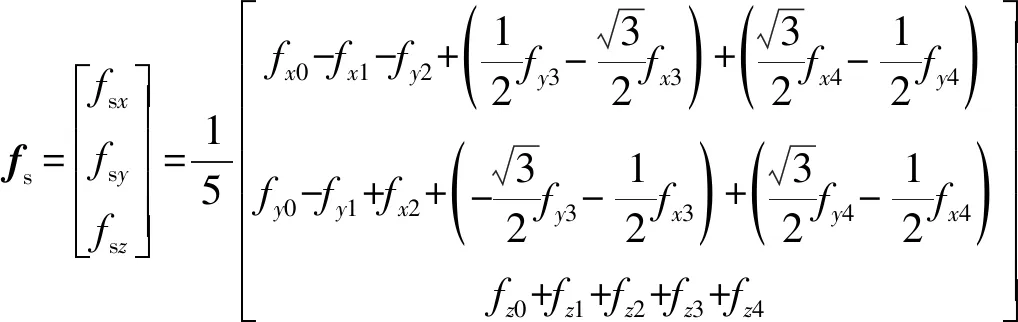
(6)

式中，为空间阵列式惯性单元输出的比力加速度矢量；s,s,s分别为为沿着,,轴的比力加速度；0,0,0分别为第0号惯性传感单元输出的，,轴比力加速度。

分析比力加速度的融合方程可知，该融合方式可以较大程度消除比力加速度的确定性误差；另外，由于轴线角度的偏差可以降低振动等非确定性的干扰，所以该融合方式可以大大降低非确定性误差，提高载体运动参数输出的精度。

2 空间阵列式惯性单元位姿解算

2.1 防冲钻孔机器人姿态解算

笔者采用四元数法来求解防冲钻孔机器人的姿态变换矩阵，进行姿态更新。四元数由1个实数单位和3个虚数单位构成，防冲钻孔机器人载体坐标系相对于导航坐标系的转动可以用四元数惟一表示:

=+++

(7)

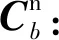
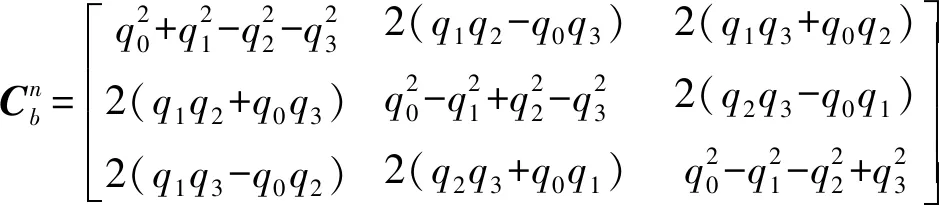
(8)

其中，，，，为实数。

四元数运动学微分方程为

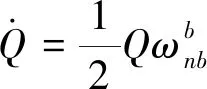
(9)

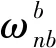
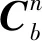
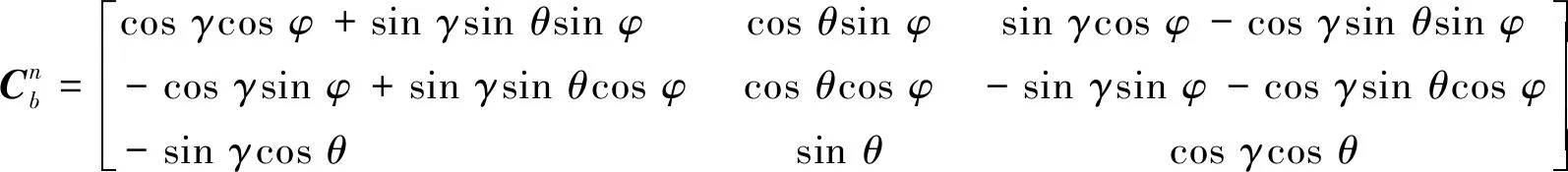
(10)

则由式(8)，(9)可以求得防冲钻孔机器人的姿态角：

(11)

由于航偏角为0°～360°，解算时出现多值对应，因此需要确定航向角的真值，有

(12)

2.2 防冲钻孔机器人速度解算

防冲钻孔机器速度解算方法是将加速度进行积分得到其速度，更新方程为

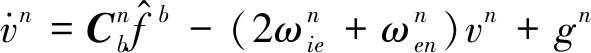
(13)

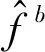
(14)

将式(14)中的变量简记为

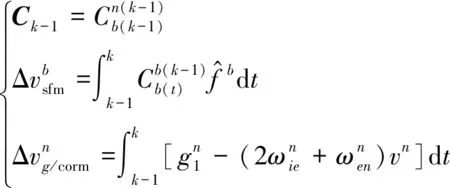
(15)

可以得到

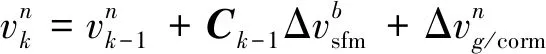
(16)

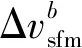
2.3 防冲钻孔机器人位置解算

防冲钻孔机器人在煤矿井下巷道中进行作业，其运动距离远小于地球的曲率半径，因此在其运动过程中可以认为地球的曲率半径不变。定义防冲钻孔机器人运动起始中心处为原点，轴指向东方向，轴指向北方向，轴垂直于当地水平面指向上。在此坐标系下描述防冲钻孔机器人的空间位置，如下：

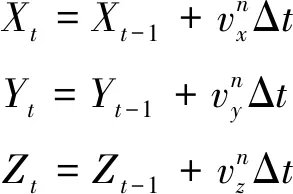
(17)

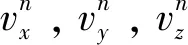
3 仿真分析

3.1 防冲钻孔机器人运行工况分析

为了验证笔者提出的防冲钻孔机器人位姿解算方法在不同运动工况下的位姿解算精度，需要获取不同运动工况下惯性传感单元的原始输出数据，作为空间阵列式惯性单元解算方法的输入，并利用解算后的位姿信息和真实的位姿信息进行对比。由于防冲钻孔机器人在井下巷道中作业工况和环境比较复杂，无法获取完善的钻孔机器人实际运行参数。因此，笔者采用数值仿真来模拟防冲钻孔机器人的不同运动工况，并给出不同运动工况下的惯性单元原始输出数据和参考速度、参考位置等防冲钻孔机器人的运动微分方程。

防冲钻孔机器人的运动工况主要有直线运动、曲线运动两种，是钻孔卸压作业时最常见的运动。为了方便运动工况的模拟，需要定义一个防冲钻孔机器人运动轨迹坐标系，轴沿运动轨迹水平向前，轴沿运动轨迹切线指向右，轴符合右手螺旋原则垂直于面指向上，笔者模拟运动工况时加速度()和角速度()的定义均在此坐标系内。防冲钻孔机器人工作过程中的运动状态变化均是由角速度()和加速度()变化引起的。

3.2 防冲钻孔机器人运动微分方程

防冲钻孔机器人运动微分方程用来求解空间阵列式惯性单元的原始输出数据和参考运动数据，包括姿态角，，，速度，位置经度、纬度、东向位移、北向位移、天向位移等。防冲钻孔机器人运动微分方程以防冲钻孔机器人运动工况分析中所述的角速度()和加速度()作为输入，直接积分求解便可获取各种运动参数。

(1)姿态角微分方程：

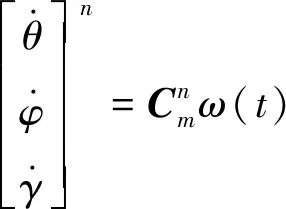
(18)

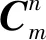
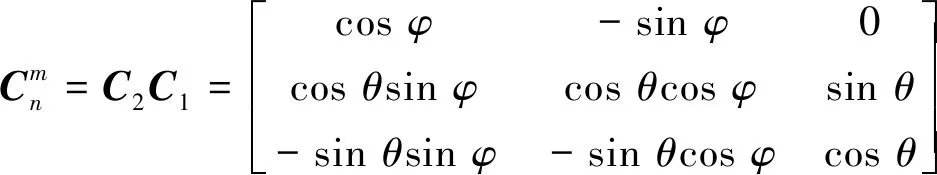
(19)

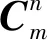
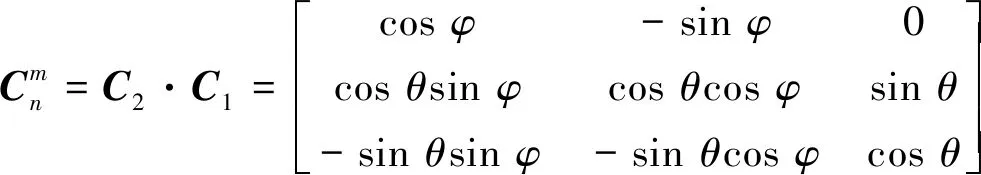
(20)

(2)速度微分方程：

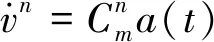
(21)

(3)位置微分方程：

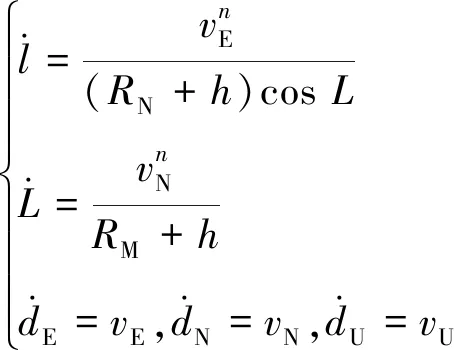
(22)

(4)惯性传感组件输出方程：

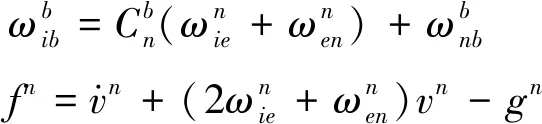
(23)

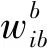
为了验证笔者提出的空间阵列式惯性单元位姿解算方法的性能，分别利用文献[20-21]中的算法(分别记为单IMU、差分式IMU)获取的防冲钻孔机器人的位姿信息，并与模拟出的防冲钻孔机器人参考位姿信息进行对比，得到位姿信息的误差曲线。由于对曲线运动模拟时已经包含直线运动，所以笔者就不再对直线运动进行解算分析。

在曲线运动仿真中，防冲钻孔机器人初始姿态角=[0 0 0]，初始速度=[0 0 0]，初始位置=[0 0 0]，初始位移=[0 0 0]，采样频率=10 Hz。设置防冲钻孔机器人沿轴方向运动28 m，沿轴方向运动0.8 m。根据以上参数，结合防冲钻孔机器人运动工况模拟方法，通过计算便可获得曲线运动的仿真参数：仿真时间500 s，0～60 s静止，60～70 s加速，加速度为0.01 m/s，70～200 s匀速，200～230 s进入曲线，航向角角速度为0.003 8 rad/s，230～270 s匀速行走，270～300 s退出曲线，航向角角速度为-0.003 8 rad/s，300～430 s匀速，430～440 s减速，加速度为0.01 m/s，440～500 s静止。最终，上述曲线运动的3种轨迹解算结果如图3所示。

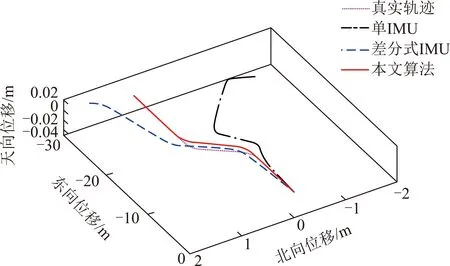
图3 曲线运动的解算结果Fig.3 Contrast result of curve motion

由图3可以看出，单个惯性单元解算方法偏差最大，特别是在运动后期，累积误差使输出轨迹明显偏离真实轨迹，差分式解算方法可以抑制一定的漂移，使得输出轨迹基本可以跟随真实轨迹形态，但是仍然存在很大的误差。笔者提出的空间阵列式解算方法能够较好地跟踪防冲钻孔机器人的基准轨迹，具有更好地解算精度。

图4为防冲钻孔机器人作模拟曲线运动时，姿态角和位移的解算误差对比结果，曲线运动是通过航偏角的多次变化而获得，因此航偏角的模拟曲线发生了多次突变。可以看出，笔者提出的位姿解算方法在三向位移和三向姿态角的解算结果均明显优于单IMU和差分式IMU解算方法。空间阵列式惯性单元解算方法在东向位移的最大误差为0.676 0 m，平均绝对误差为0.344 9 m，北向位移的的最大误差为0.016 1 m，平均误差为7.039 8×10m，天向位移最大误差为0.001 0 m，平均误差为3.086×10m；在航偏角的最大误差0.147 4°，平均误差0.030 9°，俯仰角的最大误差0.072 8°，平均误差为0.025 8°，横滚角的最大误差0.044 0°，平均误差为0.012 7°。详细对比结果见表1，可以看出，笔者提出的解算方法具有较小的位姿解算误差，说明在航偏角频繁改变的情况下，提出的解算方法能够更好地抑制惯性单元的测量误差和漂移误差，可以在不同工况下均具有更优的跟随能力和解算精度。

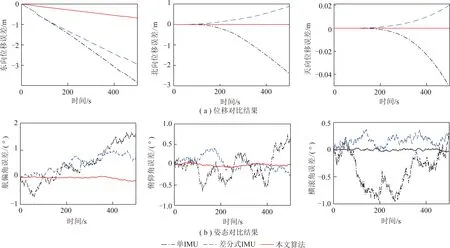
图4 模拟曲线运动的位姿解算对比结果Fig.4 Comparison of position and attitude calculation results of simulated curve motion

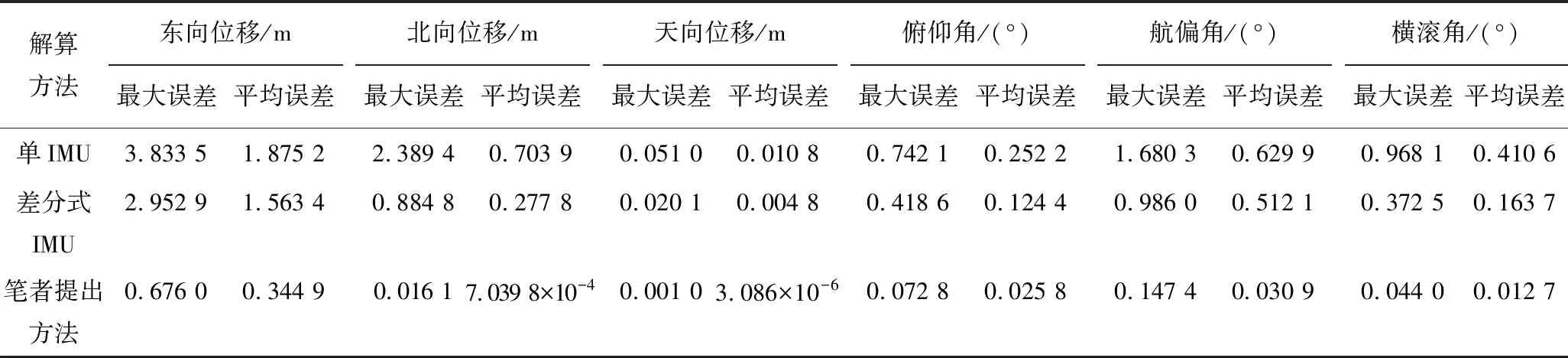
表1 模拟曲线运动的位姿解算误差对比

4 实验验证

4.1 运动工况模拟实验

为了进一步验证笔者设计的位姿解算方法在真实工况下的可行性，根据实际工况搭建了移动载体运动工况模拟实验台，进行曲线运行工况的模拟实验，如图5所示。

图5 移动载体运动工况模拟实验台Fig.5 Motion simulation test bench of mobile carrier

移动载体运动工况模拟实验台运动轨迹设置如图6所示，为曲线运动的起始点，到为直线运动阶段，与之间的距离为240 cm，在点移动平台顺时针旋转135°，与之间的距离为339.41 cm，在点，移动平台逆时针旋转135°，与之间的距离为240 cm，在顺时针旋转150°，移动平台从点直线行走277.13 cm到达终点。在运动过程中，运动平台的加速度设定为50 cm/s，速度为10 cm/s，转动角速度设定为π/20 rad/s。

图6 模拟运动轨迹Fig.6 Simulate a motion trajectory

根据以上设置的节点以及运行轨迹的长度和姿态，设定了移动平台的加速度和最大速度等参数，拟合出移动平台真实的位姿曲线，并利用笔者提出的解算方法对机器人位置和姿态进行解算，解算对比结果如图7所示。

由图7(a)～(c)可以看出，在导航坐标系中三轴方向的位移都发生了一定漂移，但笔者提出的解算方法位移平均误差明显小于单IMU和差分式IMU解算方法，在轴方向的位移最大误差为17.69 cm，平均误差为5.83 cm；在轴方向的位移最大误差为19.43 cm，平均误差8.76 cm；在轴方向的位移最大误差为2.07 cm，平均误差为0.84 cm，详细对比结果见表2。

由于实验室地面为水平平面，干扰较小，所以移动平台在轴方向的位移误差小于另外两轴方向。从轴和轴方向位移误差可以看出，在平面运动中，笔者提出的解算方法能够较好的抑制误差的漂移，减少误差的积累，从而实现对载体运动轨迹较为准确地跟踪。

由图7(d)～(f)可以看出，笔者提出的解算方法在俯仰角、航偏角和横滚角的解算精度均明显高于单IMU和差分式IMU，3个姿态角的平均误差分别为0.07°，0.15°和0.06°，详细对比结果见表3。由于曲线运动中航偏角发生多次变化，导致航偏角误差较大，符合运动特征。在航偏角多次变化的情况下，笔者提出的解算方法依然能够较为准确地解算出载体的运动姿态。

4.2 地面实验

为了进一步对防冲钻孔机器人位姿解算方法的可行性进行验证，笔者搭建了防冲钻孔机器人惯性单元位姿监测实验平台，并进行了直线行走地面实验，如图8所示。空间阵列式惯性单元被固定在空间架上，空间架被固定在防冲钻孔机器人本体上。空间阵列式惯性单元组件通过信号线与转换模块连接，转换模块通过USB接头与上位机通信。

..位置监测实验

由于车间环境复杂、空间狭小等条件的限制，无法设置防冲钻孔机器人行走过于复杂的轨迹，因此将防冲钻孔机器人加速到最大速度，然后以最大速度运行至设定位置，设定防冲钻孔机器人沿钻进方向直线行走10 m，并将前进方向设定为到导航坐标系轴正方向，垂直于机身指向右为轴正方向，轴垂直于轴和轴平面指向上。将在防冲钻孔机器人运动轨迹上设定标记点，通过记录防冲钻孔机器人到达标记的时间计算出其真实速度、加速度和位置，如图8所示。

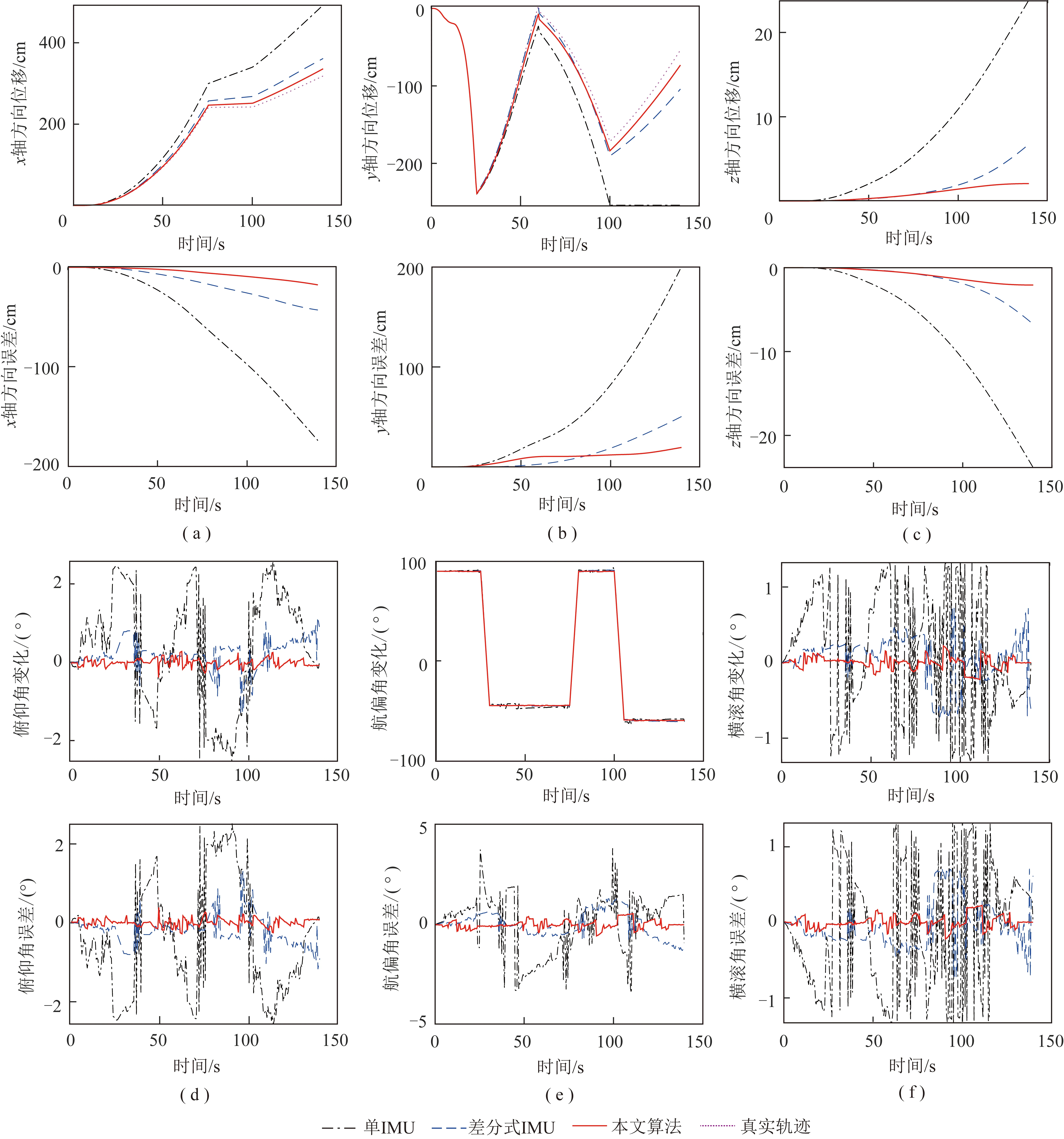
图7 位姿解算结果对比Fig.7 Comparison of position and attitude calculation results

表2 三轴方向的位移解算误差对比

表3 姿态角的解算误差对比

图8 现场实验平台Fig.8 Field experimental platform

在上位机上利用不同方法解算出防冲钻孔机器人的位置参数，将解算出的位置参数与真实轨迹进行对比，得出位置监测误差，如图9所示。

由图9可知，单IMU解算方法在轴、轴和轴方向上位移的最大误差分别为116.00，24.76和4.41 cm，平均误差分别为42.13，9.73和9.84 cm；差分式IMU解算方法的位移最大误差分别为19.03，10.91 和17.09 cm，平均误差为4.82，3.86和3.35 cm；笔者提出解算方法的位移最大误差分别为6.04，3.41和5.12 cm，平均误差1.98，1.72和1.57 cm。对比结果表明钻孔机器人的位置解算结果沿各轴线均存在一定误差，这是由于防冲钻孔机器人的位移参数是加速度经过多次积分而得到的，进而导致位置误差的漂移，但本文方法解算的位置误差最小，能够满足使用要求。

..姿态监测实验

设定与上述相同的防冲钻孔机器人运动轨迹，并对其姿态进行监测。由于防冲钻孔机器人沿直线运动，所以俯仰角、航偏角和横滚角理论上均未发生变化。由此得到姿态监测误差，如图10所示。

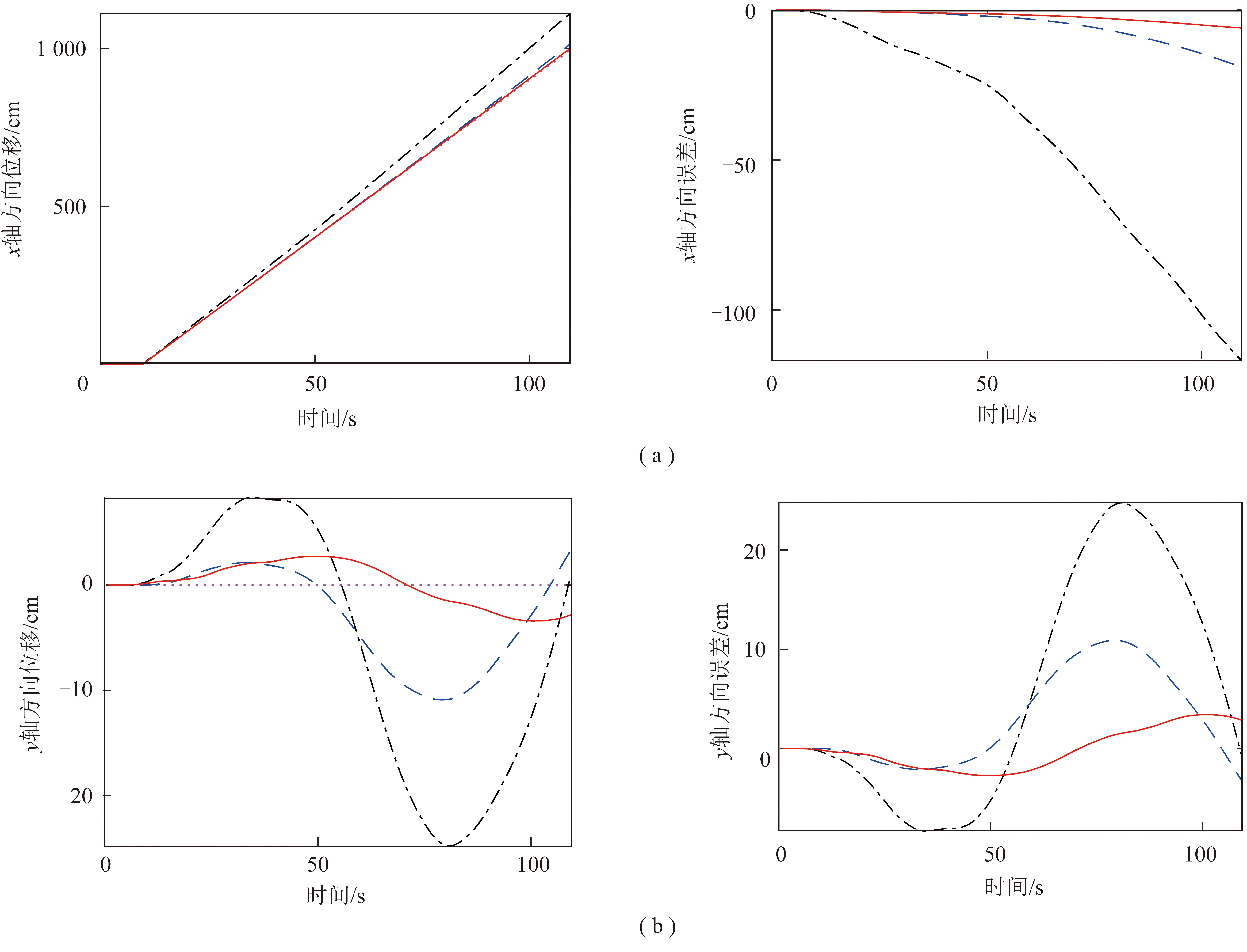
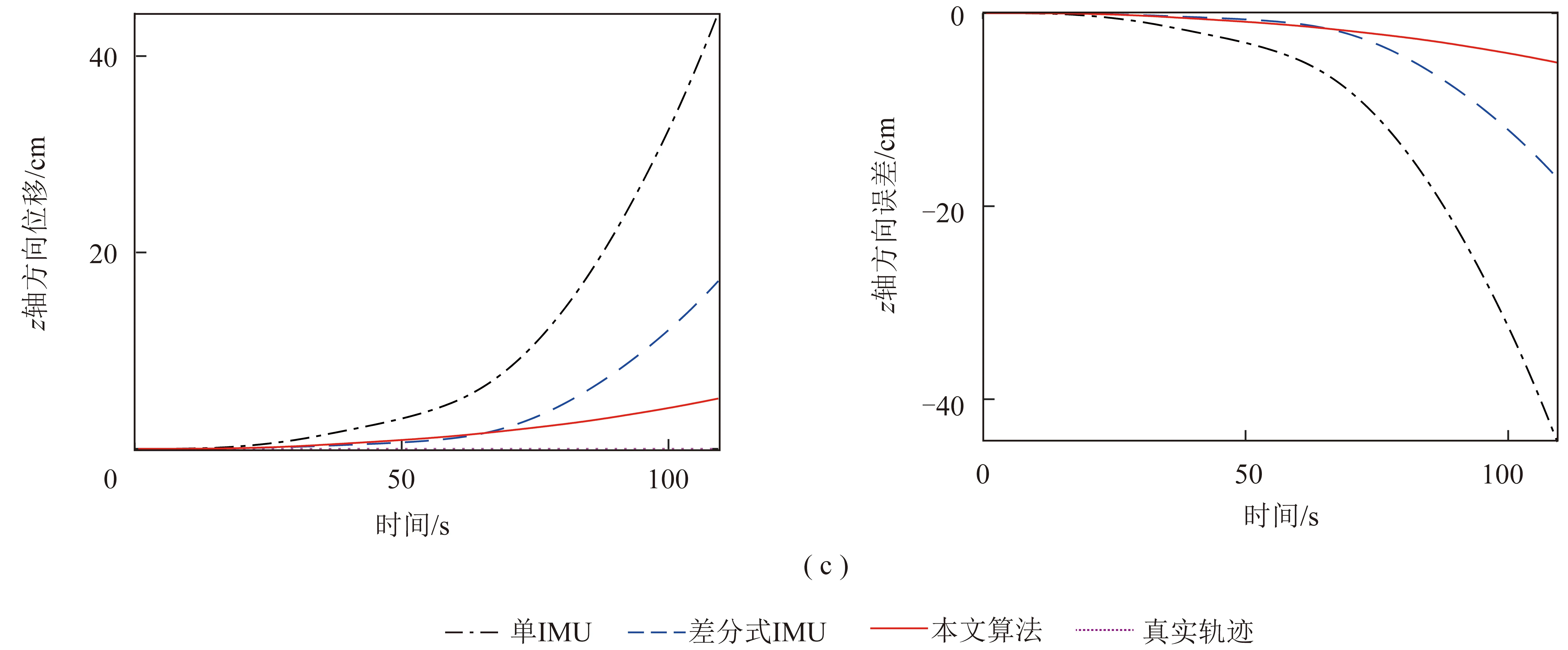
图9 位移监测结果Fig.9 Position monitoring results

从图10可以得出，单IMU解算方法在航偏角、俯仰角和横滚角方面的最大误差分别为3.57°，3.77°和4.10°，平均误差分别为0.97°，1.47°和1.52°；差分式IMU解算方法的姿态角最大误差分别为1.93°，1.31° 和1.93°，平均误差分别为0.72°，0.54°和0.71°；笔者提出方法的姿态角最大误差0.72°，0.62°和0.67°，平均误差分别为0.38°，0.25°和0.30°。由此可知，笔者所提方法的姿态角解算平均误差均小于0.5°，姿态漂移误差较小，满足防冲钻孔机器人姿态监测精度要求。

5 结 论

(1)为了精确测量防冲钻孔机器人的加速度和角速度参数，减少防冲钻孔机器人定位、定姿误差的累积，笔者提出了一种基于空间阵列式惯性单元的防冲钻孔机器人位姿解算方法，并进行了曲线运动工况下的仿真分析。结果表明：笔者提出的空间阵列式位姿解算方法在位移累积误差和姿态角平均绝对误差方面均优于原始位姿解算方法和差分位姿解算方法。

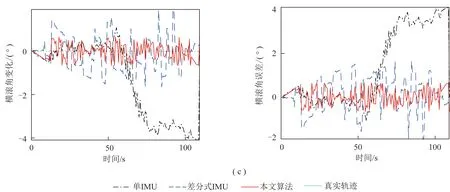
图10 姿态监测结果Fig.10 Attitude monitoring results

(2)搭建了移动载体运动工况模拟实验台，进行了曲线运动工况下防冲钻孔机器人模拟运动实验。实验结果表明：空间阵列式惯性单元解算的俯仰角、航偏角和横滚角的平均误差分别为0.07°，0.15°和0.06°；在轴、轴和轴方向的位移平均误差分别为5.83，8.76和0.84 cm，验证了笔者所提方法的适用性和可行性。

(3)搭建了防冲钻孔机器人惯性单元位姿监测实验平台，进行了防冲钻孔机器人直线行走实验，实验结果表明：所提方法解算的防冲钻孔机器人俯仰角、航偏角和横滚角的平均误差分别为0.25°，0.38°和0.30°；在轴、轴和轴方向的位移平均积差分别为1.98，1.72和1.57 cm。上述位姿解算误差均能满足防冲钻孔机器人在巷道内运动时定位和定姿精度的实际要求，验证了防冲钻孔机器人位姿解算方法的可行性和有效性。

(4)通过运动工况仿真和实验数据分析可以看出，由于非确定性误差的方向和大小均未知，本文提出的空间阵列式位姿解算方法可以有效抑制累积误差的增长速度，但难以将其完全消除。因此位姿解算误差始终在积累，无法收敛，但本文提出算法的误差累积速度远远小于其他算法。在后续研究中，笔者将通过机器视觉定时对位姿解算误差进行补偿，并利用机器学习算法对误差进行学习，进一步减小累积误差的产生。

[1] 齐庆新,李一哲,赵善坤,等. 我国煤矿冲击地压发展70年:理论与技术体系的建立与思考[J]. 煤炭科学技术,2019,47(9):1-40.

QI Qingxin,LI Yizhe,ZHAO Shankun,et al. Seventy years development of coal mine rockburst in China:Establishment and consideration of theory and technology system[J]. Coal Science and Technology,2019,47(9):1-40.

[2] 陈岩峰,李学军,吴宏斌,等. 冲击地压机理及防控现状与发展态势分析[J]. 煤炭科技,2021,42(5):70-75.

CHEN Yanfeng,LI Xuejun,WU Hongbin,et al. Control status and development trend of rockburst mechanism and prevention in China[J]. Coal Science and Technology Magazine,2021,42(5):70-75.

[3] 王国法,庞义辉,任怀伟. 煤矿智能化开采模式与技术路径[J]. 采矿与岩层控制工程学报,2020,2(1):013501.

WANG Guofa,PANG Yihui,REN Huaiwei. Intelligent coal mining pattern and technological path[J]. Journal of Mining and Strata Control Engineering,2020,2(1):013501.

[4] JOBES Christopher C. Mechanical sensor guidance of a mining machine[J]. IEEE Transactions on Industry Applications,1993,29(4):755-761.

[5] MAAREF H,BARRET C. Sensor-based navigation of a mobile robot in an indoor environment[J]. Robotics and Autonomous Systems,2002,38:11-18.

[6] LEDERGERBER Anton,HAMER Michael,D′ANDREA Raffaello. A robot self-localization system using one-wayultra-wideband communication[A]. 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems [C]. Piscataway:IEEE,2015:3131-3137.

[7] 冯佳萌,裴东,邹勇,等. 基于机器人激光定位的一种改进AMCL算法[J]. 激光与光电子学进展,2021,58(20):479-487.

FENG Jiameng,PEI Dong,ZOU Yong,et al. An improved AMCL algorithm based on robot laser localization[J]. Laser & Optoelectronics Progress,2021,58(20):479-487.

[8] 徐庆坤,王天皓,宋中越. UWB与里程计融合的室内移动机器人定位设计[J]. 机械设计与制造,2021(8):295-299,304.

XU Qingkun,WANG Tianhao,SONG Zhongyue. Design of indoor mobile robot location based on uwb and odometer data fusion[J]. Machinery Design & Manufacture,2021(8):295-299,304.

[9] 朱道俊,徐湛楠,马婷婷,等. 基于视觉和轮速计紧耦合的轮式机器人定位算法研究[J]. 传感技术学报,2021,34(7):896-903.

ZHU Daojun,XU Zhannan,MA Tingting,et al. Tightly-coupled vision and wheel odometer localization for ground vehicle[J]. Chinese Journal of Sensors and Actuators,2021,34(7):896-903.

[10] 尚磊,王杰,宋尊师,等. 基于单目ORB-SLAM2算法的煤矿搜救机器人定位研究[J]. 机床与液压,2020,48(11):49-52.

SHANG Lei,WANG Jie,SONG Shizun,et al. Research on the localization of the coal mine search and rescue robot based on the monocular ORB-SLAM2 algorithm[J]. Machine Tool & Hydraulics,2020,48(11):49-52.

[11] 蔡李花,方海峰,李允旺,等. 矿井救灾机器人自主定位方法研究[J]. 工矿自动化,2015,41(7):62-67.

CAI Lihua,FANG Haifeng,LI Yunwang,et al. Research of self-locallization method of mine rescue robot[J]. Industry and Mine Automation,2015,41(7):62-67.

[12] 赵靖. 基于卡尔曼滤波算法的采煤机惯导定位方法[J]. 工矿自动化,2014,40(10):29-32.

ZHAO Jing. Inertial navigation positioning method of shearer based on Kalman filtering algorithm[J]. Industry and Mine Automation,2014,40(10):29-32.

[13] 郭晓晶,田华,李明君. 基于卡尔曼滤波算法的采煤机惯导定位方法[J]. 煤炭技术,2015,34(7):278-280.

GUO Xiaojing,TIAN Hua,LI Mingjun. INS positioning method of shearer based on kalman filter[J]. Coal Technology,2015,34(7):278-280.

[14] 樊启高,李威,王禹桥,等. 一种采用捷联惯导的采煤机动态定位方法[J]. 煤炭学报,2011,36(10):1758-1761.

FAN Qigao,LI Wei,WANG Yuqiao. A shearer dynamic positioning method using strap down inertial navigation[J]. Journal of China Coal Society,2011,36(10):1758-1761.

[15] 杨海,李威,罗成名,等. 基于捷联惯导的采煤机定位定姿技术实验研究[J]. 煤炭学报,2014,39(12):2550-2556.

YANG Hai,LI Wei,LUO Chengming. Experimental study on position and attitude technique for shearer using SINS measurement[J]. Journal of China Coal Society,2014,39(12):2550-2556.

[16] 张羽飞,马宏伟,毛清华,等. 视觉与惯导融合的煤矿移动机器人定位方法[J]. 工矿自动化,2021,47(3):46-52.

ZHANG Yufei,MA Hongwei,MAO Qinghua,et al. Coal mine mobile robot positioning method based on fusion of vision and inertial navigation[J]. Industry and Mine Automation,2021,47(3):46-52.

[17] 温良,叶锦娇,张立亚. 煤矿救灾机器人超声波和惯性导航技术[J]. 煤矿安全,2017,515(6):127-130.

WEN Liang,YE Jinjiao,ZHANG Liya. Ultrasonic and inertial navigation technology of coal mine rescue robot[J]. Safety in Coal Mines,2017,515(6):127-130.

[18] 张璞. 煤矿井下移动机器人自主定位方法研究[D]. 西安:西安科技大学,2019:35-44.

ZHANG Pu. Research on autonmomous positioning method of coal mine mobile robot[D]. Xi’an:Xi’an University of Science and Technology,2019:35-44.

[19] 李猛钢. 面向井下钻孔机器人应用的精确定位与地图构建技术研究[D]. 徐州:中国矿业大学,2020:148-167.

LI Menggang. Research on Technologies of accurate localization and mapping for underground drilling robot application[D]. Xuzhou:China University of Mining and Technology,2020:148-167.

[20] 郭卫,张露,赵栓峰. 基于捷联惯导的采煤机姿态解算算法研究[J]. 矿山机械,2014(6):15-20.

GUO Wei,ZHANG Lu,ZHAO Shuanfeng. Study on shearer posture algorithm based on strapdown inertial navigation[J]. Mining & Processing Equipment,2014(6):15-20.

[21] 司垒,王忠宾,谭超,等. 基于差分式惯性传感组件的采煤机位姿解算法[J]. 振动. 测试与诊断,2021,41(2):220-227,406.

SI Lei,WANG Zhongbin,TAN Chao,et al. Research on differential calculation method of shearer position and attitude[J]. Journal of Vibration,Measurement & Diagnosis,2021,41(2):220-227,406.