双半环型腔MIM波导法诺共振研究

郝祥祥，霍义萍，何 倩，宋美娜，王蕴岩，崔鹏飞

(陕西师范大学 物理学与信息技术学院，陕西 西安 710119；西安市光信息调控与增强技术重点实验室，陕西 西安 710119)

由于表面等离子激元(surface plasmon polaritons, SPPs)可以克服光的衍射极限，能够实现纳米尺度下的光操控，且容易在各种金属和类金属材料表面激发，因此可以用于制造各种小型化、集成化和具有优异性能的纳米器件[1-3]。在各种等离子激元结构中，金属-绝缘体-金属(metal-insulator-metal, MIM)波导结构由于具有支持SPPs在金属-绝缘体界面传播、制作简单且适用频率范围宽等诸多优点，被认为是高性能的集成光子器件[4-5]。由于其潜在的优势，MIM波导结构被广泛用于设计光学滤波器、开关、传感器和慢光器件[6-9]。

法诺共振由连续态能级和离散态能级相干耦合产生，具有尖锐和不对称的谱线形状，并且外界轻微扰动可以引起法诺共振光谱产生剧烈的强度变化或偏移[10-11]，因此它可用在非线性光学、激光和生物传感器等领域[12-14]。共振线类型σ[15-16]定义为

σ=(β+q)2/β2+1。

(1)

其中:β=2(E-Ed)/Γd，E表示入射光能量，Ed是分立态能量，Γd是Fano共振谱线宽；q是窄的离散态和宽的连续态激发率的比值，表征Fano共振线型的不对称度。并且当q=0、∞、1和-1时，共振线型分别为洛伦兹型凹谷、洛伦兹型尖峰、先峰后谷型法诺共振和先谷后峰型法诺共振，因此只有当能量在离散态和连续态上激发概率相同时，法诺共振才会产生。调控法诺共振线型常用的方法有：在波导-微环腔系统中通过引入空气孔实现不同相位延迟[17-18]，通过改变结构的几何参数进而打破对称性[19-21]等。

传统MIM波导系统中产生法诺共振时，连续态和离散态由不同结构分别产生。在一般情况下，产生连续态的结构有墙[22-23]、短截线[24-25]等直接与主波导耦合的系统，产生离散态的结构有圆环或圆盘[26-27]、矩形腔[28-29]以及各种不规则腔[30-31]等间接与主波导耦合的系统。这些结构只能产生单独的连续态或离散态，这样就导致激发法诺共振的MIM波导系统更加复杂，不便于实际应用。

本文提出了一种简单的双半环型腔等离子激元MIM波导系统，并用有限元法对其进行了数值模拟。在该结构中产生了两个典型的法诺共振，半圆环腔可同时激发出连续态和离散态，讨论了半圆环腔宽度和耦合距离等几何参数对法诺共振峰和谷的影响。从谱线耦合角度研究了先峰后谷和先谷后峰型法诺共振的产生原理，同时实现了法诺共振的独立调控。通过在DSR结构的基础上添加腔，实现四重法诺共振，并对新产生的法诺共振实现了半独立调控。

1 模型设计

DSR结构如图1所示，左侧和右侧的半圆环分别标记为SR-1和SR-2。结构参数包括SR-1的外半径R1、内半径r1和宽度d1；SR-2的外半径R2、内半径r2和宽度d2；主波导宽度w以及SR-1和SR-2之间的耦合距离L。该2D模型中的白色和灰色区域分别代表空气(ε0=1.0)和银材料，银的相对介电常数εm由实验光学常数来表征[32-33]。输入端口(input)和输出端口(output)分别位于MIM波导的左端和右端，并在入口和出口设置两个功率监视器，分别监测入射功率(Pin)和出射功率(Pout)，并将透射率定义为T=Pout/Pin。四周边界条件设置为完美匹配层(perfectly matched layer, PML)，用来吸收电磁波,银和空气区域分别用细化和较细化的自由三角形网格划分，扫描步长设置为1 nm，用有限元分析软件COMSOL Multiphysics 5.4对该等离子激元结构光谱响应特征进行仿真计算。

图1 DSR结构示意图Fig.1 Structure diagram of the DSR

在MIM波导耦合谐振器系统中，当SPPs耦合到腔中且谐振器满足谐振条件时，在特定的谐振波长下形成稳定的驻波，谐振波长由驻波公式[34-35]确定

(2)

其中：C=π(R+r)/2是半圆环腔的有效长度;正整数m代表SPPs的阶数;φ是反射光束的相位差；Rf是MIM波导中有效折射率的实部。

2 仿真分析

2.1 DSR结构的透射特性

图2a为DSR结构的透射谱，结构参数设置如下：R1=150 nm,r1=100 nm,R2=200 nm,r2=150 nm,L=100 nm,w=50 nm。当系统中仅存在SR-1腔或SR-2腔时，其透射特性如图2a中的黑线和蓝线所示，可以看到半圆环腔的透射谱包含透射率迅速和缓慢变化两个波段，因此半圆环腔能同时激发离散谱和连续谱，并且当增大半圆环腔半径时，透射谱产生红移并保持相同的谱线形状。根据上述规律，将两个不同半径的半圆环腔耦合到一个波导系统中，其透射谱如图2a中红线所示，可以看到2个典型的法诺共振被激发出来，结合离散态和连续态共振位置可知，869 nm处的法诺共振(FR1)由SR-1产生的离散态和SR-2产生的连续态耦合形成，1 194 nm处的法诺共振(FR2)由SR-1产生的连续态和SR-2产生的离散态耦合形成。

e图为SPPs先经过SR-1再经过SR-2;f图为SPPs先经过SR-2再经过SR-1。

图2b、2c分别表示FR1的峰和谷处的归一化磁场能量分布图，能量主要耦合在SR-1腔中。图2d、2e分别表示FR2的峰和谷处的归一化磁场能量分布图，能量主要耦合到SR-2腔中。结合透射谱图和上面两组磁场能量分布图可以得到结论:窄离散态对法诺共振的形成起决定作用。比较图2c、2e中两个法诺共振谷的磁场能量分布图可知，FR1谷处的能量只在SR-1腔中出现，SR-2腔中完全没有，这符合上述结论，但是FR2谷处却有少许能量存在于提供连续态的SR-1腔中，这不符合上述结论。为了探究这种现象，改变SPPs经过半环腔的顺序得到FR2谷处的磁场能量分布图，如图2f所示。与图2e不同，这里SPPs先经过SR-2再经过SR-1，此时透射谱不发生变化并且SR-1中没有能量，故图2e SR-1腔中的少许能量并不参与FR2谷的形成，因此SPPs经过半环腔的顺序会对法诺共振的磁场能量分布产生影响。

2.2 SR-1腔和SR-2腔的耦合距离对DSR结构透射谱的影响

图3a为改变SR-1腔和SR-2腔耦合距离L时的透射谱，图3b为法诺共振峰和谷处共振波长随L的变化图。当L=250 nm时，DSR结构激发了新的法诺共振(FR0)，并且可以看到谷1和谷2的共振位置不随L发生改变，而峰0、峰1、峰2随着L的增大发生红移，因此法诺共振谷不随耦合距离而改变，法诺共振峰随着耦合距离产生线性红移。对比图2a可以发现，FR1和FR2峰的位置都红移到对应谷的右侧，由L=100 nm时的先峰后谷型法诺共振转变成L=250 nm时的先谷后峰型法诺共振，这是因为当L=100 nm时，FR1和FR2由离散态谷的左侧下降段与连续态耦合形成，而当L=250 nm时，FR1和FR2由离散态谷的右侧上升段与连续态耦合形成。从图3a中还可以看到，随着L的增大，峰0和谷1的共振位置逐渐接近，当L=500 nm时，峰0和谷1的共振波长相同，此时FR0消失，如前所述，改变耦合距离L会导致法诺共振谷的位置不变而法诺共振峰的位置红移，即当峰和谷的共振波长相等时，法诺共振消失。图3c为不同L时法诺共振峰透射率的变化情况，可以看到峰0和峰1的透射率都实现了先增大、后减小的过程，并且出现透射率最大值，故可以通过调控参数L来获得所需要的透射率。因此，耦合距离L不仅可以对法诺共振峰的位置和透射率进行调控，还可以改变法诺共振的线型，这种优异的效果可以用在光开关领域。

图3 不同L时的DSR结构透射谱(a)，不同L时法诺共振峰和谷处的波长(b)和透射率(c)变化图Fig.3 Transmittance spectrum of the DSR structure with different L(a), wavelength (b) and transmittance (c) of peaks and dips of the Fano resonance with different L

2.3 SR-1腔的宽度对DSR结构透射谱的影响

图4a为改变SR-1腔宽度d1时的透射谱，图4b为法诺共振峰和谷处共振波长随着d1的变化图，其中d1=R1-r1，且R1=100 nm保持不变。随着d1的增大，峰2和谷2的共振位置不发生变化，峰1和谷1的共振位置发生蓝移。由于SR-2腔各参数保持不变，FR2的共振波长几乎不变，从公式(2)中可以看出，当结构和材料确定，Rf是定值，对于同一法诺共振，m是定值，此时共振波长只与共振腔的有效长度C有关。由于d1增大导致r1减小，故SR-1腔的有效长度C减小，从而使得共振波长λm减小，产生蓝移现象。当d1=26 nm时，谷1和峰2的共振波长相等，此时FR2消失。当d1=61 nm时，谷1和峰1的共振波长相等，此时FR1消失。图4c展示了不同d1下法诺共振峰峰1和峰2透射率的变化情况，随着d1的增大，谷1和峰1的共振位置逐渐接近，导致峰1透射率逐渐减小直至为0，谷1和峰2的共振位置逐渐远离，导致峰2透射率逐渐增大，在交点处，两个法诺共振的透射率相同。因此，可以通过调节SR-1腔的宽度d1对FR1进行独立调控。

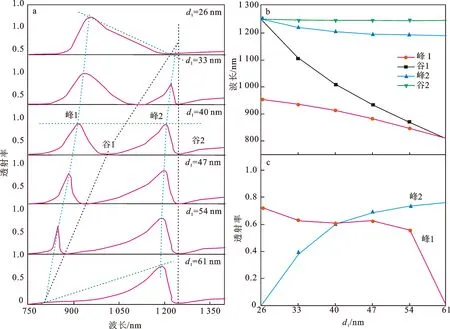
图4 不同d1下的DSR结构透射谱(a)，不同d1下法诺共振峰和谷处的波长(b)和透射率(c)变化图Fig.4 Transmittance spectrum of the DSR structure with different d1 (a), wavelength (b) and transmittance (c) of peaks and dips of the Fano resonance with different d1

2.4 SR-2腔的宽度对DSR结构透射谱的影响

图5为改变SR-2腔宽度d2时的透射谱，其中d2=R2-r2，且R2=150 nm保持不变。随着d2的增大，FR1不发生变化，而FR2发生蓝移。由于SR-1腔各参数保持不变，FR1的共振位置几乎不变，d2增大导致r2减小，故SR-2腔的有效长度C减小，从而使得共振波长λm减小，产生蓝移现象。当d2=64 nm时，谷2和峰2的共振波长相同，此时FR2变成洛伦兹凹谷；当d2<64 nm时，FR2是先谷后峰型法诺共振；当d2>64 nm时，FR2是先峰后谷型法诺共振。结合之前规律可知，法诺共振的形成主要是离散态起主导作用，并且离散态透射谱以谷处波长为对称轴，谷值左侧透射率迅速下降，而谷值右侧透射率迅速上升。结合图5中的FR2可知，当d2<64 nm时，离散态谷的右侧上升段与连续态耦合，导致了先谷后峰型法诺共振；当d2>64 nm时，离散态谷的左侧下降阶段与连续态耦合，产生了先峰后谷型法诺共振。因此，可以通过调节SR-2腔的宽度d2来对FR2进行独立调控。

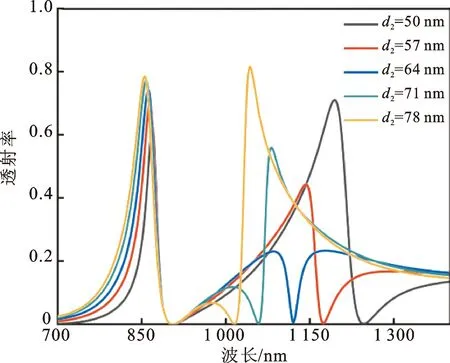
图5 不同d2下的DSR结构透射谱Fig.5 Transmittance spectrum of the DSR structure with different d2

2.5 环境折射率对DSR结构透射谱的影响

由于法诺共振具有对环境高度灵敏的反应，因此我们通过改变填充介质研究DSR结构的传感特性，并采用折射率灵敏度S(sensitivity)和品质因数F(figure of merit) 来表征等离子激元结构的传感性能[36-38]，分别定义为

S=Δλ/Δn，

(3)

F=ΔT/TΔn。

(4)

其中：Δλ、ΔT和Δn分别为透射率、共振波长和介质折射率的单位变化量;S的物理意义为每改变一个单位折射率等离子体能量的变化情况，S越大代表该结构的灵敏度越高;F值越大代表共振窗口越窄、共振线型越尖锐以及传感器精度越高。图6a为改变介质折射率n时的透射谱，随着n的增大，法诺共振出现显著红移并保持相同的谱线形状。图6b显示了法诺共振峰和谷处波长与折射率之间良好的线性关系，通过线性拟合，得到峰1、谷1、峰2和谷2的灵敏度分别为850、890、1 180和1 260 nm/RIU。图6c为DSR结构的品质因数随波长变化图，可以看到在FR1和FR2处的F值分别为17 473 RIU-1和6 218 RIU-1。因此，所提出的结构可以用作监测环境折射率、环境温度和液体浓度的传感器。

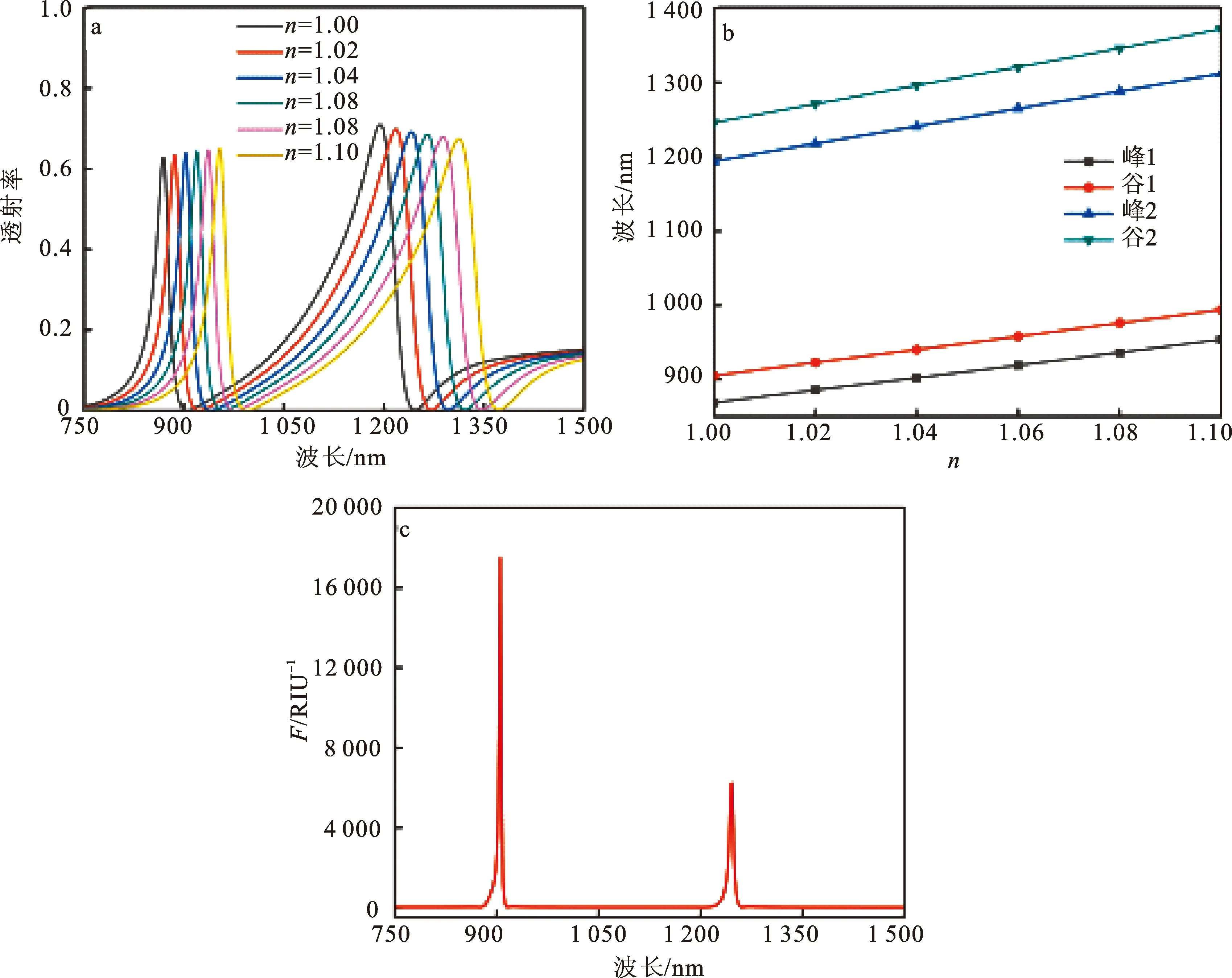
图6 不同折射率n下的DSR结构透射谱(a)，法诺共振峰和谷处波长变化图(b)，F随波长变化图(c)Fig.6 Transmittance spectrum(a) of the DSR structure with different refractive indices n, wavelength of peaks and dips of the Fano resonance with different refractive indices n(b),the F value of DSR structure varies with wavelength(c)

2.6 DSR-T结构的透射特性

如图7a所示，通过在DSR结构SR-2腔的下方添加一个底边长为I、高为J的三角形腔，形成双半环加三角结构(double semi-ring and triangle, DSR-T)。图7b为DSR-T结构的透射谱，其中I=2R2=400 nm，J=250 nm，其他参数值与图2中相同，可以看到在原有FR1和FR2的基础上产生了两个新的法诺共振，其中645 nm和1 464 nm处的法诺共振分别命名为NFR1和NFR2。图7c和图7d为不同J下DSR-T结构的透射谱：在图7c中，随着J的增大，NFR1产生红移而FR1和 FR2保持不变，实现了对NFR1的独立调控；同样在图7d中，随着J增大，NFR2发生红移而FR1和FR2保持不变，因此NFR2也可以被独立调控。在DSR-T结构中，由于SR-1腔和SR-2腔各参数保持不变，FR1和FR2的共振位置不随三角腔几何参数的变化而变化，同样NFR1和NFR2被三角腔所激发，与双半环型腔无关，因此该系统中的法诺共振具有独立可调的优势。DSR-T结构能够激发多重法诺共振和实现半独立调控，因此可以用在多通道滤波器等领域。

图7 DSR-T结构示意图(a)，DSR-T结构的透射谱(b)，不同J下的DSR-T透射谱(c,d)Fig.7 Structure diagram of the DSR-T (a), transmittance spectrum of the DSR-T structure (b), transmittance spectra of the DSR-T structure with different J(c,d)

3 结论

本文设计了一种简单的双半环型腔波导耦合结构(DSR)，并在单个半环型腔中同时激发出离散态和连续态能级，通过两种状态的相干耦合，实现了2个具有高透射率的法诺共振。通过对其透射谱和磁场能量的分析，得到了一些规律。

从SPPs耦合结果来看，激发离散态能级的腔对法诺共振的形成起决定性作用。通过改变结构参数，研究了耦合距离L、SR-1和SR-2的宽度d1和d2、环境折射率n对法诺共振透射谱线的影响，结果表明：L增大会使FR1和FR2的峰红移而谷不变，并且当峰和谷的共振波长相等时，法诺共振消失。d1增大会使FR1蓝移而FR2不变，d2增大会使FR2蓝移而FR1不变，因此FR1和FR2可以被独立调控。n增大会使两个法诺共振线性红移，并得到最大1 260 nm/RIU的折射率灵敏度和最大17 473 RIU-1的F值，这在传感器领域能够得到广泛的应用。

在DSR-T结构中得到了四重法诺共振，并对新的法诺共振实现了独立调控。本文提出的结构具有简单且易于制造、法诺共振透射率高以及可调性好等诸多优点，但也存在法诺共振的波长范围较大、品质因数较小以及不适用于特殊高精度领域等缺陷。