新型自适应广义特征向量估计算法及其特性分析

徐中英 高迎彬 孔祥玉

①(火箭军工程大学导弹工程学院 西安 710025)

②(中国电子科技集团公司第五十四研究所 石家庄 050081)

1 引言

作为一门重要分析工具，广义特征值分解(Generalized Eigen-Decomposition， GED)已经广泛应用于盲源分离[1]、脑电波分析[2]、影像分割[3]、阵列天线[4]、数据分类[5]等诸多领域。给定一个矩阵束(Ry，Rx)，则GED问题就是求解满足式(1)的关系向量w和标量λ

其中，Ry和Rx是两个n×n维正定的Hermitian矩阵。满足方程式(1)的向量w和标量λ分别记为矩阵束(Ry，Rx)的广义特征向量和广义特征值。虽然传统的奇异值分解等代数方法可以解决GED问题，但是这些方法计算复杂度较高，而且要求矩阵束(Ry，Rx)是已知的。而在实时信号处理领域，由于传感器输出的是信号当前时刻的采样值，需要对矩阵束进行在线估计和更新，因此发展自适应GED算法就很有必要。近些年来，基于神经网络的自适应GED算法成为国内外的研究热点。相比传统的代数方法，神经网络类算法具有在线运算、计算复杂度低、能够处理高维数据和非平稳信号等优点[6—8]，已经成为该领域内的主流研究方向。

基于神经网络的GED算法将线性神经元的突触权向量作为广义特征向量的估计结果，通过构造合适的更新规则使得权向量能够收敛到信号自相关矩阵束的广义特征向量。基于3层前向神经网络，Yang等人[9]提出了一个递归最小二乘算法，然而该算法在估计自相关矩阵时需要用到所有信号数据，因此存储器需求量特别大。Liu等人[7]则利用递归神经网络(Recurrent Neural Network， RNN)技术提出了最大和最小广义特征值同时估计的RNN算法，该算法收敛速度较慢。Attallah等人[10]采用降秩法提出了降秩广义特征向量提取(Reduced- rank Generalized EigenVector Extraction， R-GEVE)算法，该算法通过在当前时刻的信号采样值与上一时刻的广义特征向量估计值构成的降秩空间里进行搜索来完成广义特征向量估计，由于该算法搜索空间小于实际的信号子空间，因此算法收敛速度较慢；通过将GED问题转化为特征值分解问题，Tanaka等人[11]采用幂函数法算法提出了快速的算法，虽然该算法解决了收敛速度的问题，但算法容易产生数值不稳定现象；通过对Oja-Xu算法进行改进，Nguyen等人[12]提出了稳定的GED算法，该算法虽然平衡了收敛速度与稳定性之间的关系，但是其稳定性是靠添加模值归一化来完成的，增加了算法的计算量。为了避免频繁的模值归一化操作，Li等人[13]通过对权向量添加隐性模值约束提出了自稳定的GDM(Generalized Douglas Minor component analysis)算法，但是该算法收敛速度较慢。目前，发展快速稳定的自适应GED算法仍是该领域内值得研究的问题。

算法的特性分析包括稳定性分析、动态特性分析等内容。稳定性分析通过李雅普诺夫函数法研究算法所有平衡点的渐进稳定性，确定出稳定的平衡点并建立起稳定的平衡点与所需广义特征向量之间的关系；明确算法的最终收敛结果，是发展算法的必要环节[14]。动态特性分析是指利用确定性离散时间(Deterministic Discrete Time， DDT)方法研究算法在迭代过程中权向量的运动轨线和变化规律，给出保证算法收敛的边界条件，是研究算法特性的重要部分[15]。以往DDT方法研究对象主要是特征值分解算法[16—18]。相比传统特征值分解算法，GED算法研究对象从单个矩阵变为了两个矩阵构成的矩阵束，算法形式的复杂导致动态特性分析难度相应增加。因此有必要研究如何利用DDT方法对GED算法进行动态特性分析。

为了进一步提升算法性能并完成算法的特性分析，本文首先提出了一个单维广义特征向量估计算法，然后分别利用李雅普诺夫函数法完成了算法的稳定性分析和DDT方法完成了算法的动态特性分析，最后利用膨胀技术将所提单维算法拓展为多维广义特征向量提取算法。

2 单维算法的提出

3 单维算法的性能分析

算法的稳定状态是指经过很多次迭代运算后权向量的最终收敛结果，此时算法中权向量停止更新。根据优化理论：算法只有可能在平衡点处达到稳定状态，因此可以通过研究算法平衡点的稳定性来确定所提算法式(5)的最终收敛结果，相关结论由如下定理给出。

定理1 对所提单维算法式(5)而言，当且仅当w=±vn时算法是渐进稳定的，而其他平衡点是不稳定的，其中vn是矩阵束(Ry，Rx)最小广义特征值λn对应的广义特征向量。

证明 参见附录1。

定理1表明：所提算法式(5)唯一稳定的平衡点vn是吸引子，而其他平衡点是排斥子。因此在经过若干次迭代运算后，算法式(5)中权向量必然收敛到矩阵束(Ry，Rx)最小广义特征值对应的广义特征向量vn。在计算得到广义特征向量vn后，其对应的广义特征值可以通过λn=(vnTRyvn)/(vnTRxvn)计算得到。

4 单维算法的动态特性分析

4.1 权向量模值的上下界

算法式(5)在迭代过程中，权向量模值的有界性证明将通过如下两个定理来完成，其中定理2证明所提算法权向量模值存在上界，定理3则证明权向量模值存在下界。

4.2 权向量分量的动态特性分析

本节将利用定理2和定理3的权向量模值有界性结论来分析zi(k)的动态特性，相关结论如下。

证明 参见附录4。

根据式(7)和引理1可以得出结论：在迭代过程中，zi(k)的正负号并不会改变。即如果初始化值zi(0)＞0，则对于所有的k ≥0，均有zi(k)＞0；反之如果zi(0)＜0，则对于所有的k ≥0，均有zi(k)＜0。不失一般性，这里只考虑zi(k)＞0的情况(zi(k)＜0情况下证明相类似)。

4.3 权向量的动态特性分析

5 多维广义特征向量估计算法

单维算法式(5)只能计算矩阵束最小广义特征值对应的广义特征向量，为了能够计算多维广义特征向量，这里采用膨胀技术提出了多维广义特征向量估计算法，其计算步骤见表1。

表1 多维广义特征向量估计步骤

6 仿真实验

本节将通过3个实验来对所提算法进行验证。第1个实验用所提单维算法来对广义特征向量进行估计并与一些算法进行对比；第2个实验检验所提多维算法的性能；第3个实验验证算法的动态特性分析结论。

这里利用文献[13]中方法随机生成如式(13)和式(14)的两个6×6维对称正定矩阵矩阵束(Ry，Rx)的最大广义特征值λ1=1.7880，最小广义特征值λ6=0.1770且其对应的广义特征向量为

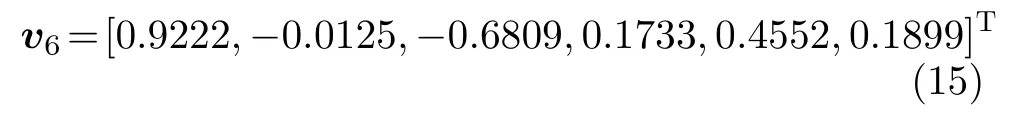
在算法迭代过程中，通过如下方向余弦来衡量权向量与目标广义特征向量之间的相似度

从式(16)可得：当方向余弦DC收敛到1时，权向量w(k)与目标广义特征向量v是相重合的。

6.1 单维广义特征向量估计实验

本实验利用GDM算法[13]、RNN算法[7]和所提单维算法来估计矩阵束(Ry，Rx)的广义特征向量v6。3个算法采用相同的初始化参数：学习因子η=0.1，初始化权向量w(0)是随机产生的，其模值归一化为0.5。为了描述算法更加真实的性能，这里进行了100次独立仿真实验。图1是最后一次迭代过程中所提算法权向量各元素的运动曲线，图2分别给出了3种算法的方向余弦曲线(100次实验的平均值)。从图1 可得：权向量最终收敛结果为w=[0.9222，-0.0125，-0.6809，0.1733，0.4552，0.1899]T=v6， 即权向量已经与广义特征向量相重合。从图2中可以看出方向余弦曲线最终收敛值也是1，这与图1中结果是相一致的。对比图2中所提算法与其他两个算法的迭代过程可以发现：所提单维算法的收敛速度均快于其他两个算法。

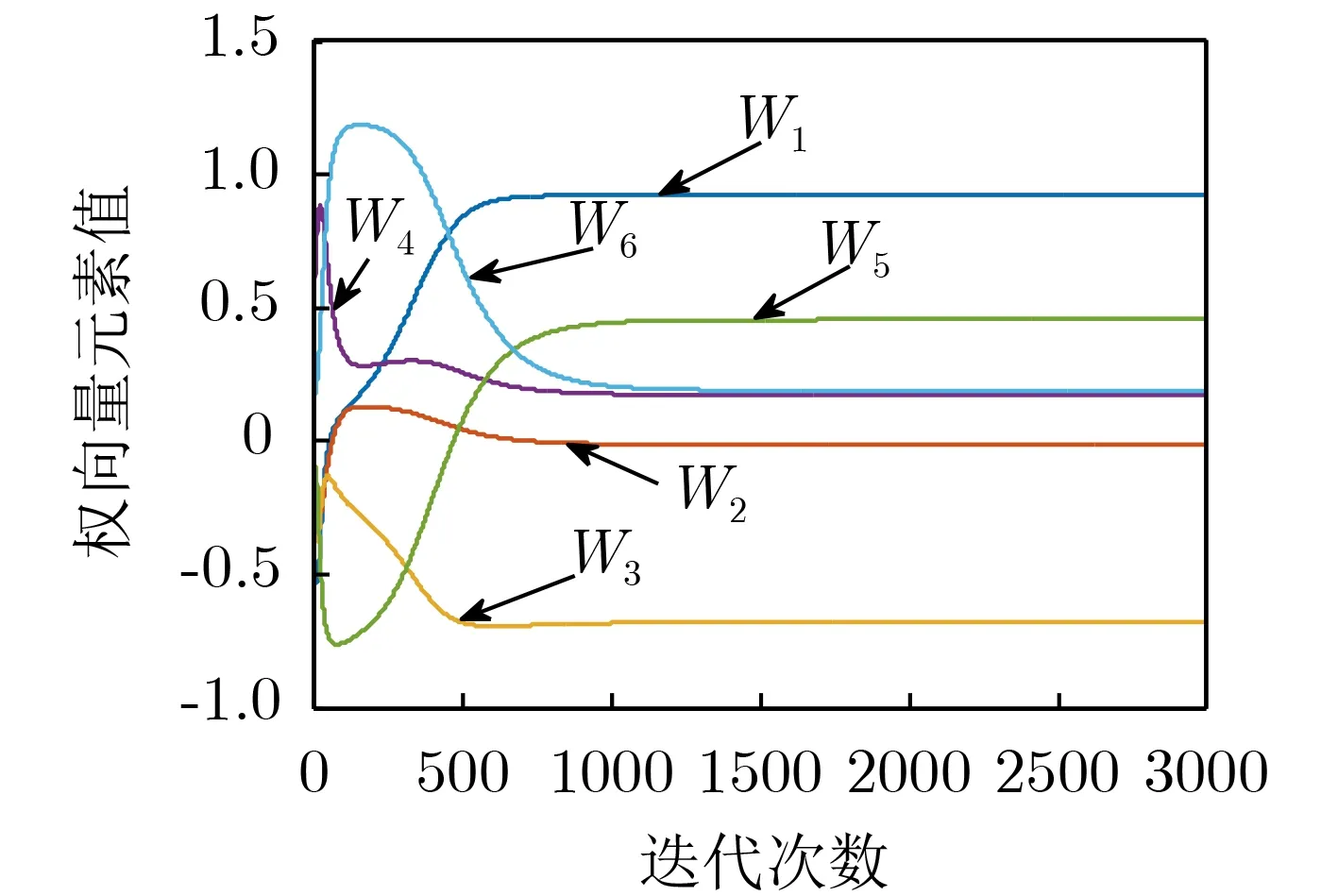
图1 权向量各元素的运动曲线

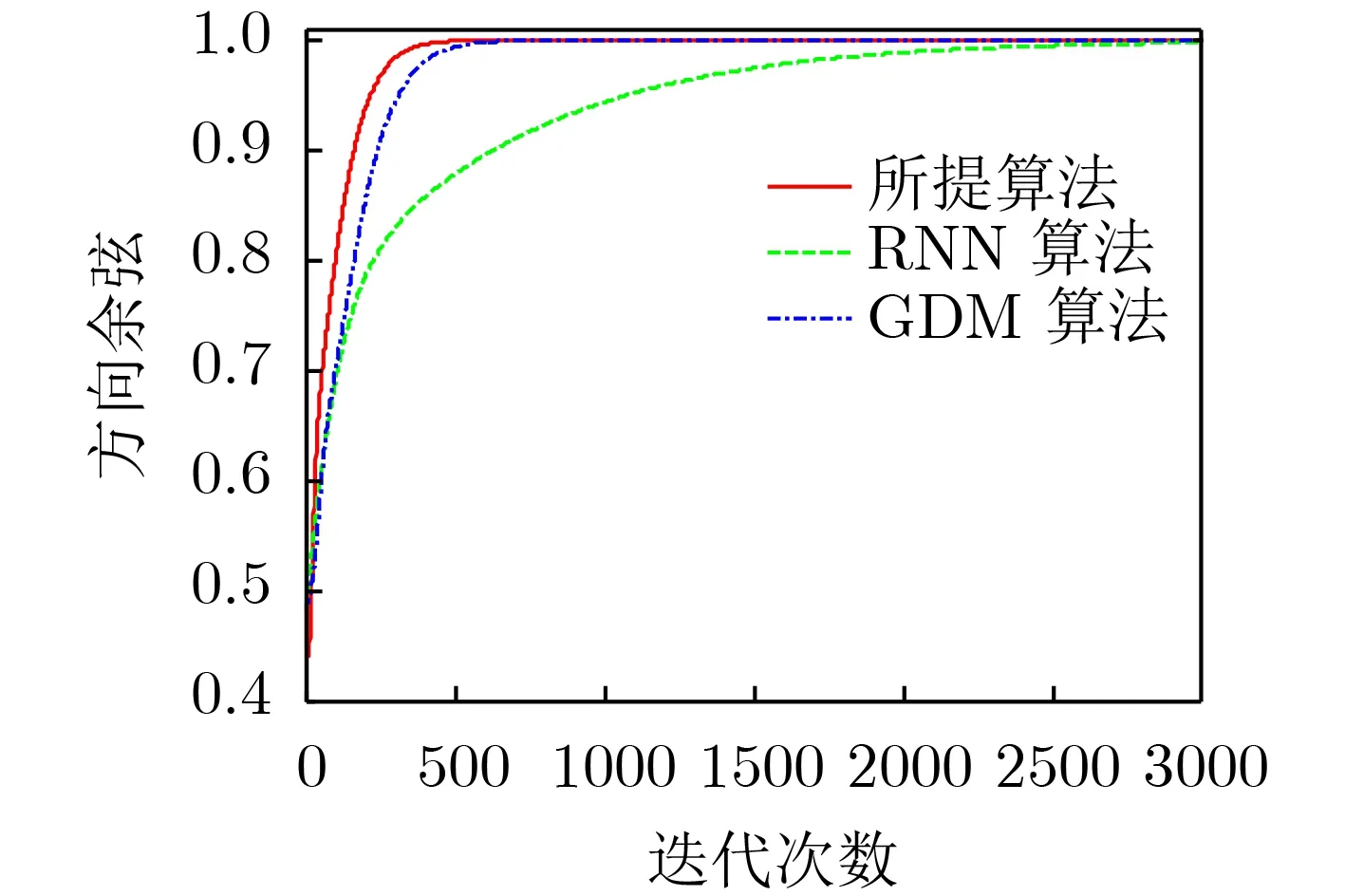
图2 3个算法的方向余弦曲线

6.2 多维广义特征向量估计实验

本实验利用第5节所提多维GED算法来计算由式(13)和式(14)组成的矩阵束(Ry，Rx)最小4个广义特征值对应的广义特征向量(即v6，v5，v4，v3)。算法的初始化参数设置如下：学习因子η=0.02，常值σ=2＞λ1，初始化权向量是随机产生的，其模值归一化为0.5。图3给出了利用所提多维算法估计的4个广义特征向量的方向余弦曲线，该曲线也是100次独立实验的平均值。

从图3可以看出：4条方向余弦曲线最终均收敛到了单位1，即所提算法中权向量准确地收敛到了所需的广义特征向量的方向，该实验表明所提算法能够有效地对多维广义特征向量进行估计。由于所提算法对广义特征向量的计算是串行提取，因此可以根据需要增加或者减少所需要估计的广义特征向量的个数。

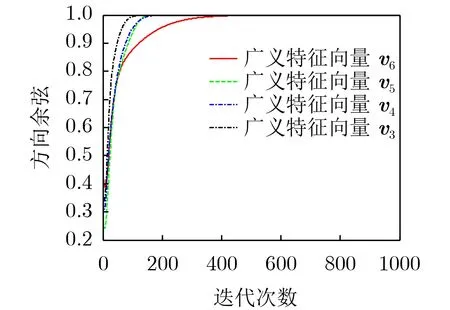
图3 4个广义特征向量的方向余弦曲线

6.3 算法动态特性分析实验

本实验主要是对第4节中的动态特性分析结论进行验证。这里利用式(5)对6.1节中的矩阵束(Ry，Rx)的广义特征向量进行估计，实验中学习因子设置为η=0.1，显然此时学习因子满足定理4中η≤0.2和ηλ1≤0.2的要求。图4是当w0=[-0.1878，-0.5908，-0.145，0.3064，0.2316，0.7385]T时获得的权向量分量曲线。从图4中可以看出，当经过很多次迭代计算后zi(k)(i=1，2，3，4，5)逐渐趋于0，而z6(k)最终收敛到了单位1。该动态曲线与引理2和引理3中的结论是相一致的，进而证明了第4节算法动态分析的有效性。

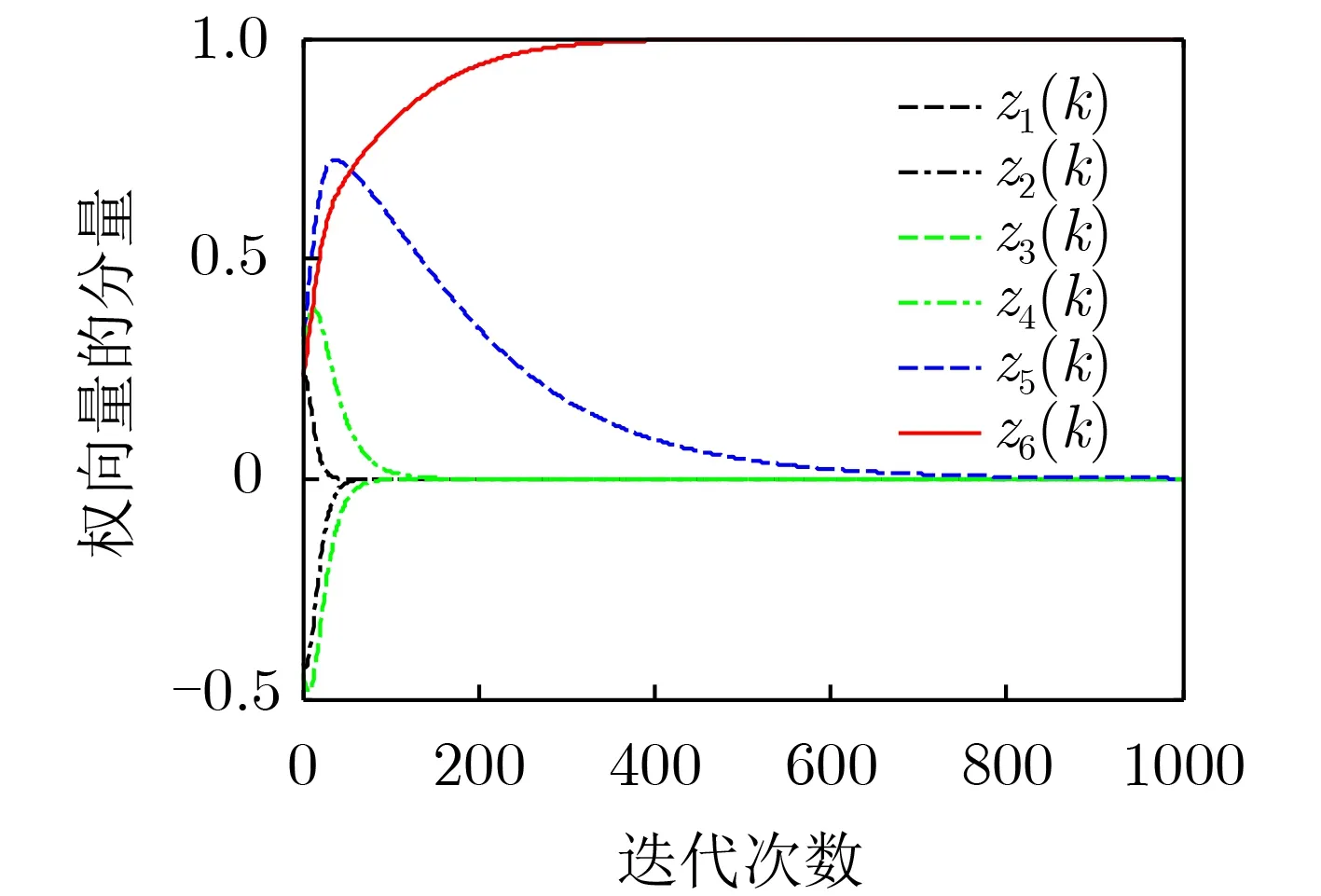
图4 权向量的分量曲线

7 结论

GED是信号处理领域内重要的分析工具。本文首先提出了新型单维广义特征向量估计算法；利用李雅普诺夫函数法分析了算法所有平衡点的稳定性，建立了算法最终收敛结果与目标广义特征向量之间的联系；通过研究权向量在广义特征向量上的投影完成了算法的动态特性分析，给出了保证算法收敛的充分条件；基于膨胀技术将所提单维算法扩展为多维GED算法。仿真实验表明所提算法能够有效估计矩阵束的单维或多维广义特征向量，而且在收敛速度上具有一定的优势。

附录1