脉冲型近场地震作用下列车简支梁桥的耦合振动
2022-02-24雷虎军刘伟
雷虎军,刘伟
(福建工程学院 土木工程学院,福州 350118)
中国自北向南密集分布着5大地震区和23条地震带,地震发生频率高、强度大。随着高速铁路网的不断加密,高速铁路桥梁跨越断层或位于断层20 km范围内的情况不可避免,在该区域发生的地震称为“近场地震”。《铁路桥梁抗震设计规范(2009版)》指出,当桥梁必须跨越断层时,宜采用小跨度、低墩高的简支梁桥。因此,简支梁桥在近场区域的高速铁路线路中得到了广泛应用,该类桥型在设计使用年限内遭遇近场地震作用的几率很大。
相比中远场地震,近场地震最显著的特征是含有高能速度脉冲[1],会激发结构显著的位移响应。由于高速列车对桥上线路的平顺性和稳定性要求极高,近场地震速度脉冲产生的大位移对高速铁路桥梁十分不利。关于近场地震速度脉冲引起的铁路桥梁抗震问题已受到广泛关注。例如,王炎等[2]采用远场地震叠加速度脉冲的方法生成不同参数的近场地震,系统研究了铁路减震桥梁的弹塑性地震响应,结果表明,考虑速度脉冲后,铁路桥梁的减震效果会显著降低;陈令坤等[3-4]分别输入一组近场脉冲型地震和一组远断层地震,对比分析了高铁简支梁桥的弹塑性地震响应,结果表明,当脉冲周期与结构的弹塑性周期接近时,会加剧桥梁的非线性地震响应;他们还研究了轻轨交通桥梁在近场地震竖向和水平地震联合作用下的弹塑性地震反应,结果表明,竖向分量对轻轨车低频运行安全性的地震响应影响较大;刘正楠等[5]通过建立高铁连续梁线桥一体化模型,分别输入3条近场地震和3条远场地震进行仿真计算,研究了摩擦摆支座的隔震效果,结果表明,近场地震的脉冲效应会加剧隔震连续梁桥邻梁的碰撞;陈伟等[6]以台湾Chi-Chi地震记录作为输入,分析了高铁连续梁桥的地震易损性,结果表明,近场地震的破坏力更强。除此之外,众多研究表明[7-11],地震在威胁桥梁本身安全的同时还会诱发显著的行车安全问题。然而,到目前为止,涉及近场地震速度脉冲对高速铁路简支梁桥及桥上列车动力响应影响的研究很少,这对于近场区域高铁桥梁的运营安全十分不利。
关于近场脉冲型地震的研究大多受限于历史记录少、记录台站分散等因素,人工模拟近场脉冲型地震动是突破该瓶颈的重要途径。关于近场脉冲型地震动的模拟,学者们提出了一些简化方法。其中,Alavi等[12]首先根据近场地震动与脉冲型地震作用下结构动力响应具有相似性的特点,提出用简化脉冲表示近断层地震动,并在之后提出了等效脉冲的概念;Makris等[13]采用三角函数模拟了3种典型的速度脉冲波形,并验证了该脉冲波形与实际近场地震记录具有较高的吻合度;王炎等[2]在远场地震动的基础上叠加三角函数脉冲,模拟了不同参数的近场地震动;杨庆山等[14]用简化函数表示等效速度脉冲,并将地震波的低频和高频成分叠加,合成了近场地震动。在上述方法中,文献[2]的方法最为实用,且模拟效率高,笔者参考该方法合成近场脉冲型地震动。

1 近场脉冲型地震动模拟
1.1 脉冲模型
采用Makris等[13]提出的3类典型脉冲模型与底波叠加,生成近场脉冲型地震动,如图1所示。
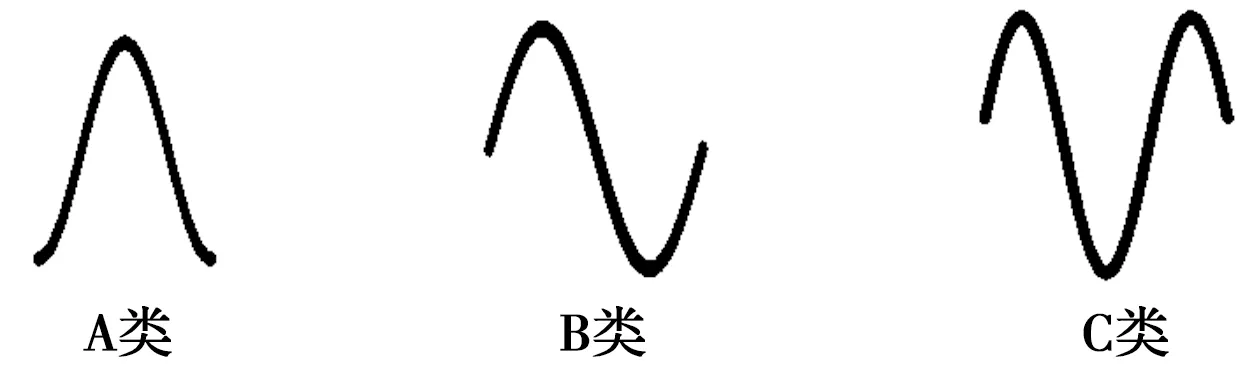
图1 Makris脉冲模型
图1中,A类、B类和C类分别为单半波型、双半波型和三半波型脉冲,可采用三角函数法模拟,其数学表达式分别为:
A类单半波脉冲模型
(1)
B类双半波脉冲模型
v(t)=Vpsin(ωpt),0≤t≤Tp
(2)
C类三半波脉冲模型
(3)
式中:Vp、Tp、ωp分别为速度脉冲的幅值、周期和圆频率。脉冲形状参数n与相位角φ有关,两者之间的关系应满足式(4),当n=1时,φ=0.069 7π;当n=2时,φ=0.041 0π。取n=1进行研究。
cos[(2n+1)π-φ]+[(2n+1)π-2φ]sinφ-
cosφ=0
(4)
在模拟等效速度脉冲的过程中,根据Somerville[15]和Mavroeidis[16]提出的回归关系式式(5)、式(6),通过震级Mw和震中距R即可确定脉冲周期Tp和脉冲幅值Vp。
ln(Vp)=-2.31+1.15Mw-0.5ln(R)
(5)
lg(Tp)=-2.9+0.5Mw
(6)
1.2 合成过程
采用MATLAB 2018a软件编写近场脉冲型地震动的模拟程序。其中,在将底波和速度脉冲叠加时,使底波的速度峰值与速度脉冲的首波峰值重合,其基本流程如图2所示。
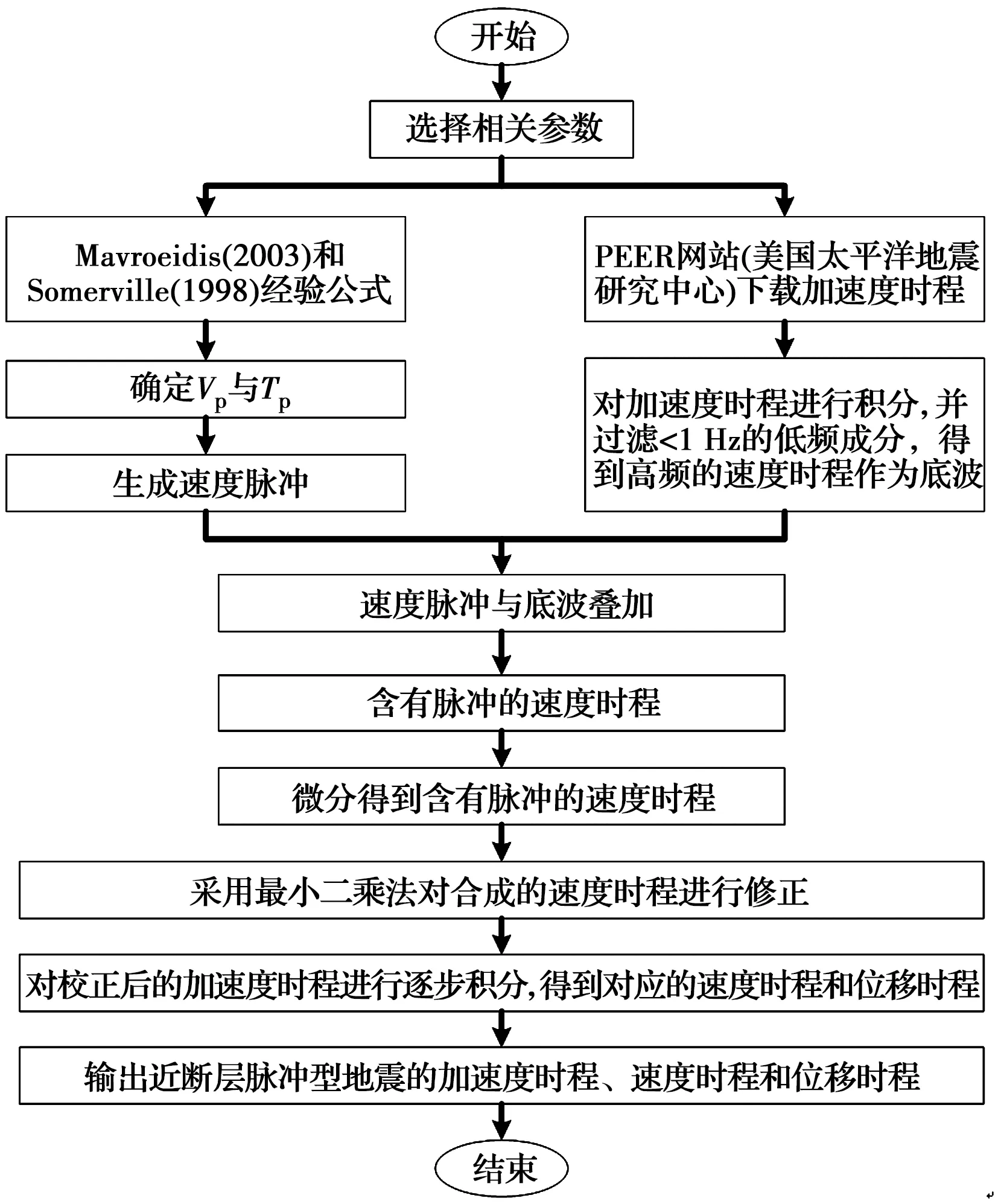
图2 近场脉冲型地震动合成流程图
1.3 合成实例及验证
以1940年El Centro波为例,叠加A类脉冲合成近场脉冲型地震动。其中,El Centro波的记录台站为El Centro Array #9,分量为I-ELC180。假设震级为7.0,震中距为10 km,将震级和震中距参数带入式(5)、式(6)即可解得脉冲周期和脉冲速度峰值分别为4.0 s、0.98 m/s。近场脉冲型地震波的合成过程依次如图3~图5所示。

图3 El Centro底波
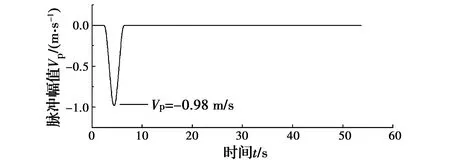
图4 等效速度脉冲
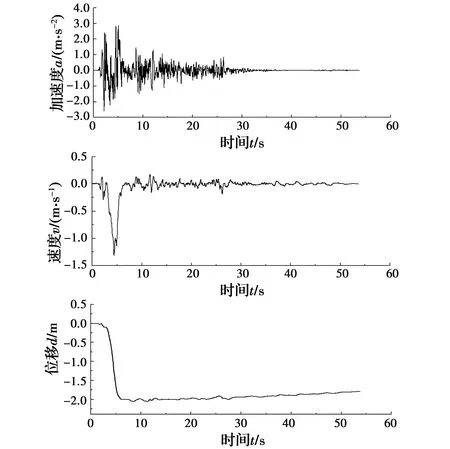
图5 合成波
通过对比合成波和典型历史近场脉冲型地震波(Chi-Chi地震,1999年,震级为7.6,记录台站为TCU068,分量为TCU068-E)的加速度反应谱特征来验证合成波的可靠性。为便于比较,将所有地震波的PGA调至0.3g,合成波的脉冲周期与历史记录波一致,均为5 s。历史记录波调幅后的加速度和速度时程如图6所示,加速度反应谱对比如图7。
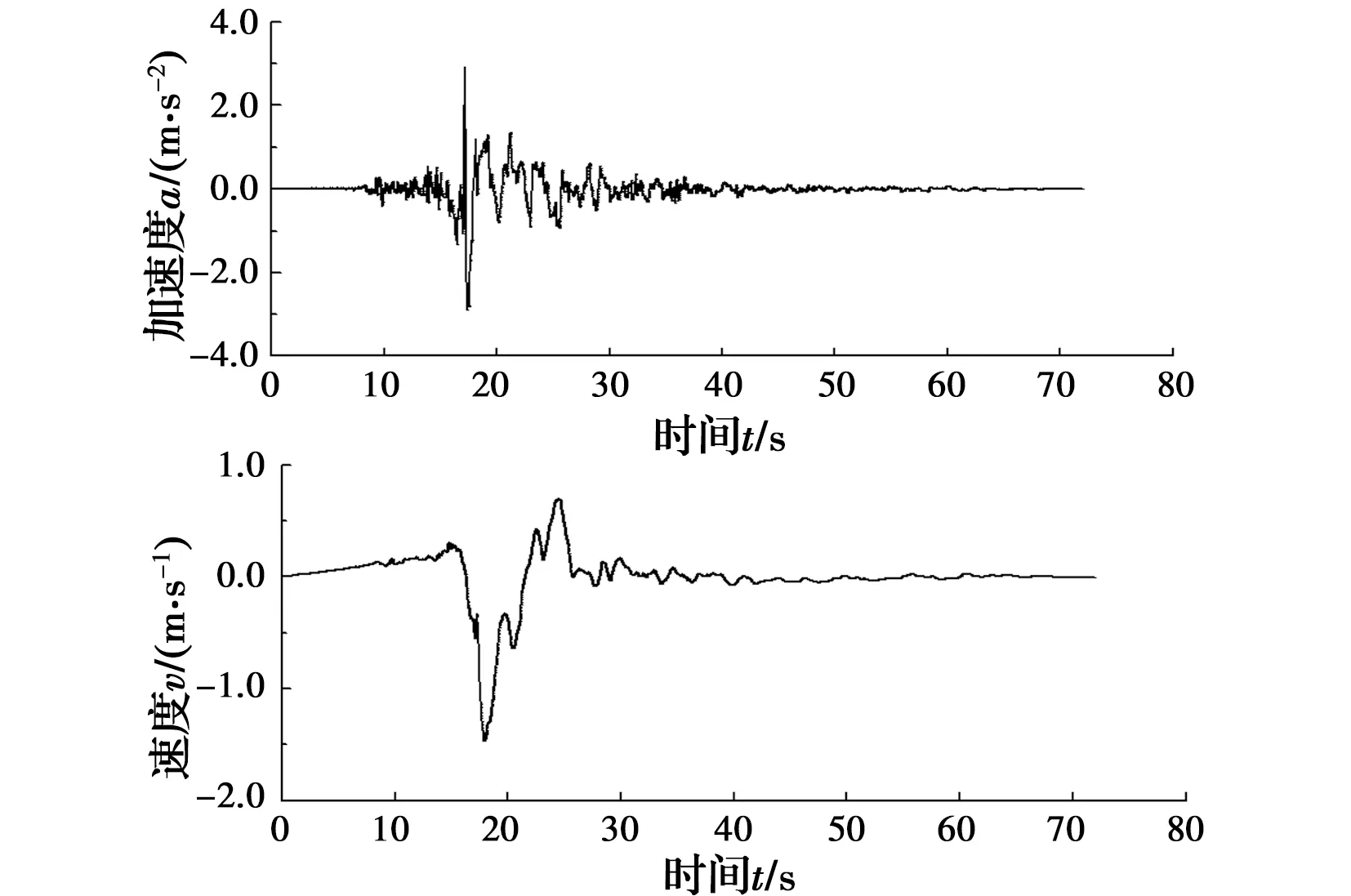
图6 TCU068-E地震波
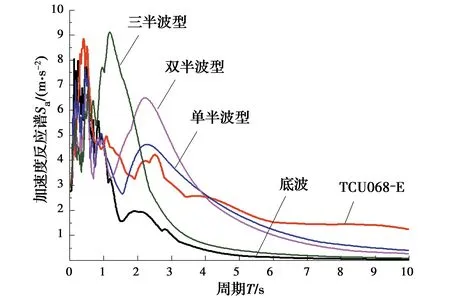
图7 加速度反应谱对比
由图7可知,合成波的加速度反应谱具备了底波和历史记录波的特征。在底波的卓越周期附近,历史记录波、合成波与底波的加速度反应谱峰值接近;随着脉冲类型从单半波变化至三半波,合成波的加速度反应谱逐渐增大,其中单半波型合成波与历史记录波最为接近,原因是单半波型的合成波和历史记录波同属一种脉冲类型,因此按脉冲类型将模拟近场地震动分类可提高合成的准确性。此外,模拟的所有近场地震动的PGV/PGA均大于0.2,满足近场地震动的基本判断标准,由此可验证合成方法及编制的近场脉冲型地震生成程序有效。

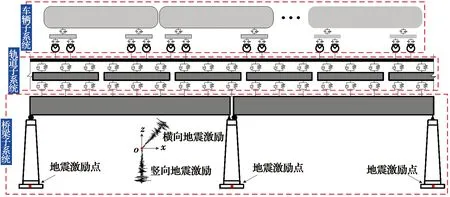
图8 地震车轨桥动力模型
(7)

3 算例研究
3.1 计算条件
以10孔跨径32 m的典型高速铁路简支梁桥为例进行仿真计算,设计时速为350 km/h。主梁为单箱单室,箱梁长32.6 m、高3.5 m,顶板宽12 m,底板宽5 m;桥墩采用圆柱墩,墩高10 m、直径4 m。采用Midas Civil 2020建立桥梁分析模型后,将其导入TTBSAS程序即可得到仿真计算的桥梁模型,单跨简支梁桥模型如图9所示。轨道采用板式无砟轨道,车辆采用8节编组的高速列车,轨道和车辆的详细参数见文献[19]。
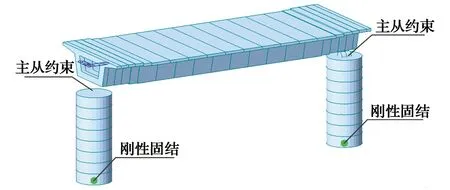
图9 单跨简支梁桥模型
根据该桥的场地类别,以El Centro地震波为底波,合成不同参数的近场地震动作为输入。其中,合成波包含3种脉冲类型,每种脉冲类型考虑7种脉冲周期,每种脉冲周期分11种脉冲幅值,合成了近场脉冲型地震动共231条,如表1所示。地震波依次按脉冲类型、脉冲周期、脉冲幅值的顺序进行编号。不同参数的单半波脉冲近场地震动加速度反应谱对比见图10和图11。

表1 近场脉冲型地震动列表
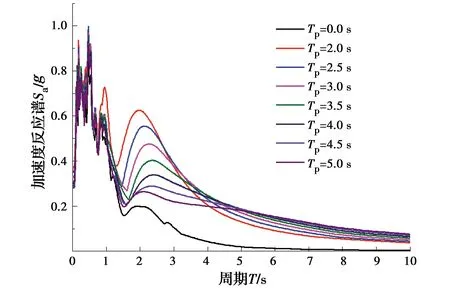
图10 不同脉冲周期的单半波脉冲近场地震动反应谱对比
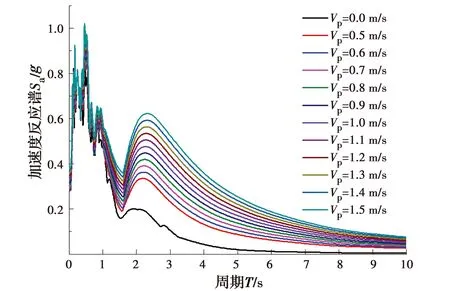
图11 不同脉冲幅值的单半波脉冲近场地震动反应谱对比
由图10和图11可见,考虑速度脉冲后,合成波的加速度反应谱均大于底波,且随着脉冲周期的增大,速度脉冲的影响逐渐减弱;而脉冲幅值越大,其地震加速度反应谱越大。将上述231条合成波和底波沿桥梁横向、竖向按1∶0.65的比例同时输入TTBSAS程序进行仿真计算,考虑列车过桥的3种车速:250、300、350 km/h,即可得到不同脉冲类型、脉冲周期和脉冲幅值近场地震作用下车桥系统的动力响应。
3.2 脉冲类型的影响分析
首先考察脉冲类型对车桥系统动力响应的影响。保持脉冲周期3.0 s、速度脉冲峰值1.0 m/s不变,假设地震发生时刻与列车上桥时刻相同。图12给出了列车以车速300 km/h过桥时不同脉冲类型近场地震作用下桥梁跨中的横向位移时程对比。

图12 横向位移时程对比
由图12可见,考虑速度脉冲后,桥梁跨中的横向位移时程波形与无脉冲时相似,但位移峰值有增大的趋势。相比单半波型,双半波型和三半波型近场地震作用下桥梁位移的幅值增大更明显。不同脉冲类型近场地震作用下列车以不同车速过桥时桥梁跨中的动力响应幅值统计见表2。
由表2可得:1)不同车速下,考虑近场地震速度脉冲后,桥梁的横(竖)向位移幅值和横(竖)向加速度幅值均比无脉冲时大,且桥梁位移响应的增幅大于桥梁加速度。例如,当车速为250 km/h时,桥梁横、竖向位移的最大增幅分别为11.5%和24.1%,而桥梁横、竖向加速度的最大增幅仅2.1%和1.4%;
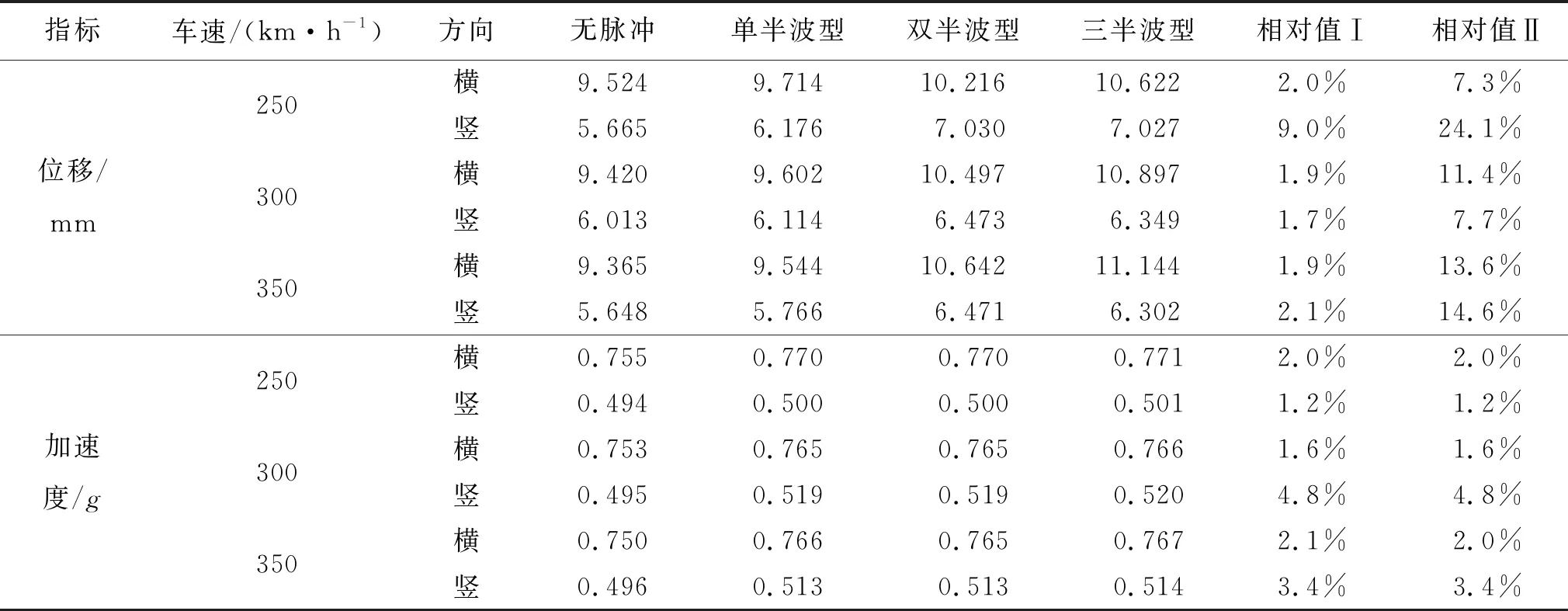
表2 不同脉冲类型地震作用下桥梁跨中动力响应幅值对比
2)随着脉冲类型从单半波型变化至三半波型,其动力响应有逐渐增大的趋势,且单半波型近场地震作用下的桥梁动力响应明显小于双半波型和三半波型。进一步考察脉冲类型对列车行车安全性指标[20](指标1:脱轨系数;指标2:轮重减载率;指标3:轮对横向力)的影响,如图13~图15所示。
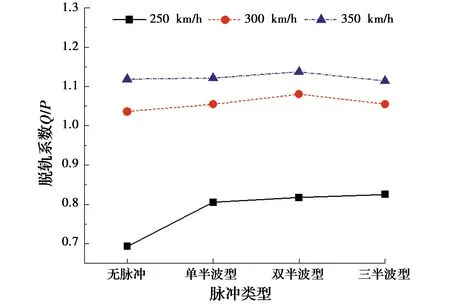
图13 脱轨系数随脉冲类型的变化
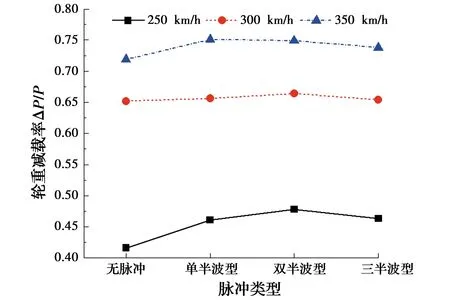
图14 轮重减载率随脉冲类型的变化
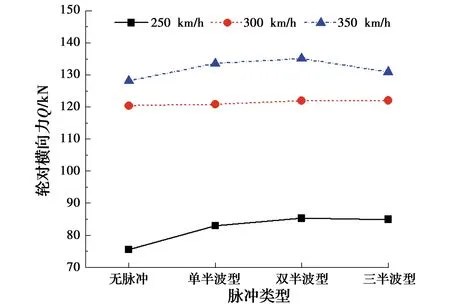
图15 轮对横向力随脉冲类型的变化
由图13~图15可得:1)考虑速度脉冲后,列车的行车安全性指标均比无脉冲时大,且在行车速度为250 km/h时增幅最为显著,其中,指标1~3的最大增幅分别为16.2%、10.8%、9.8%;2)随着脉冲类型的变化,不同车速下列车的行车安全性指标有先增大后减小的趋势,但变化幅度不大;3)列车的行车安全性指标均随车速的增大而急剧增大,且增幅大于脉冲类型。由此可见,脉冲类型对列车行车安全性指标有影响,但影响小于桥梁位移。
3.3 脉冲周期的影响分析
考察脉冲周期对车桥系统动力响应的影响。脉冲周期分别取0.0、2.0、2.5、3.0、3.5、4.0、4.5、5.0 s,其中,0.0 s表示远场地震动。为便于对比,计算时保持速度脉冲峰值1.0 m/s不变,脉冲类型假设为双半波型。不同脉冲周期近场地震动作用下桥梁系统的动力响应幅值对比如图16~图18所示,列车的行车安全性指标对比如图19~图21所示。
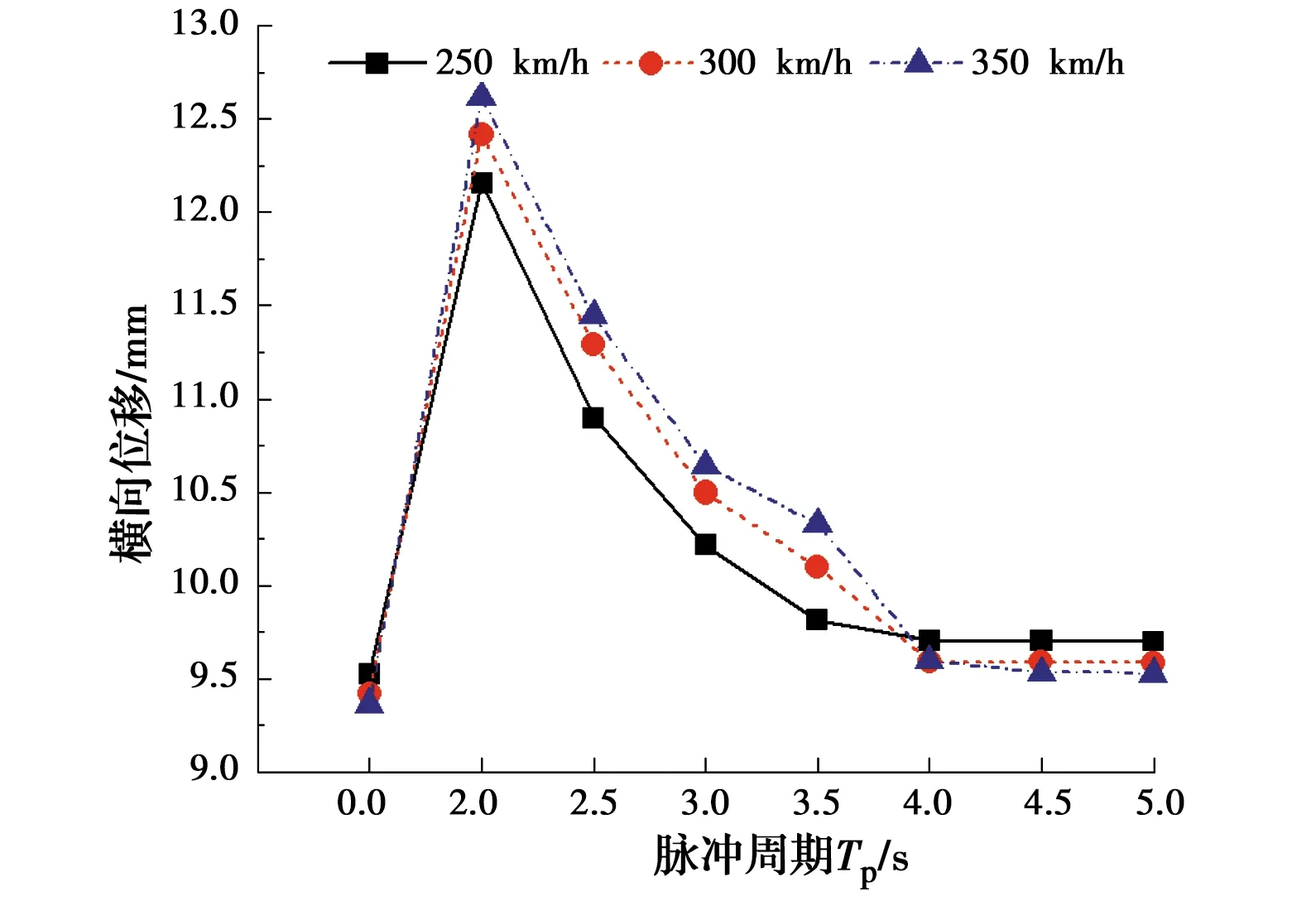
图16 桥梁跨中横向位移随脉冲周期的变化
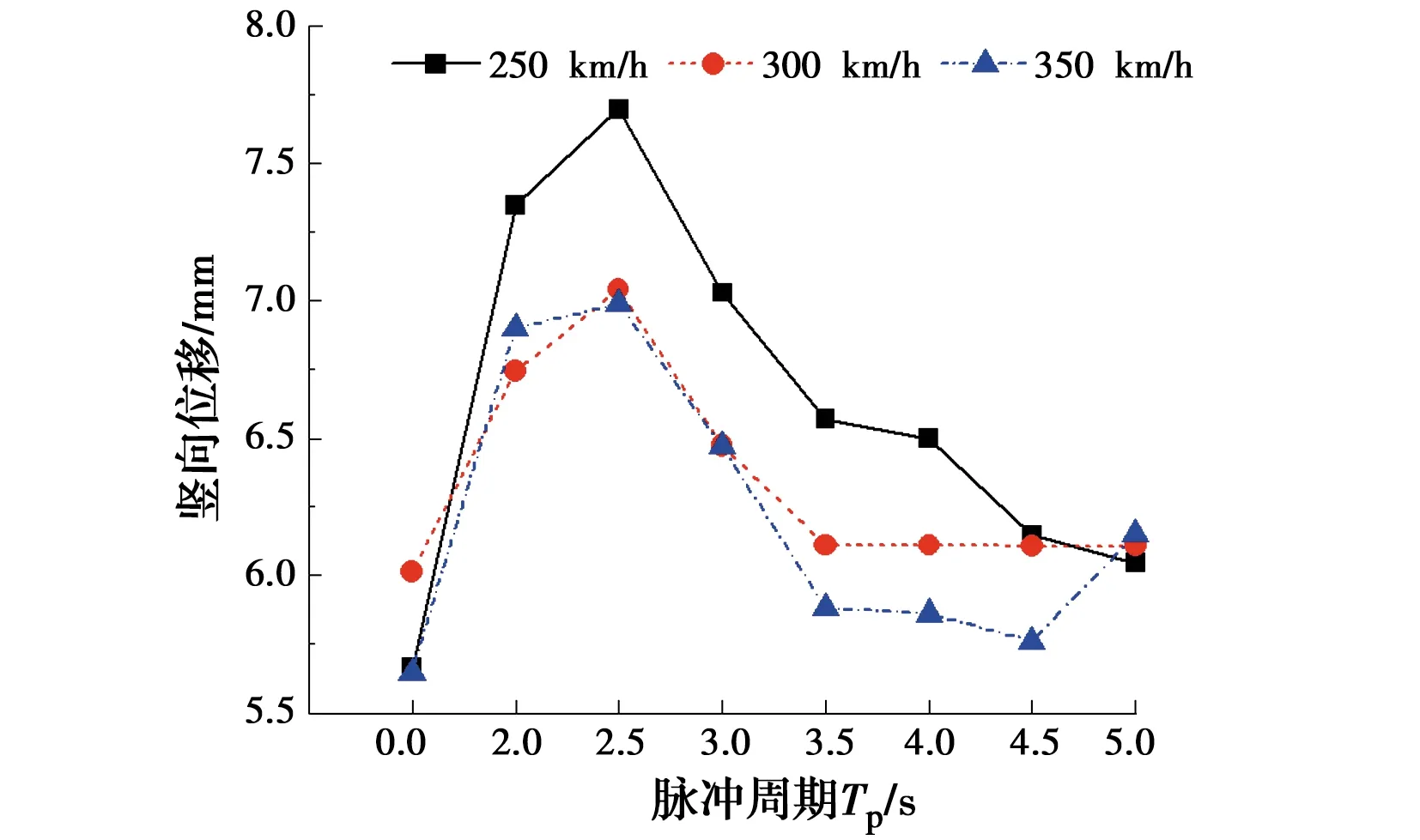
图17 桥梁跨中竖向位移随脉冲周期的变化
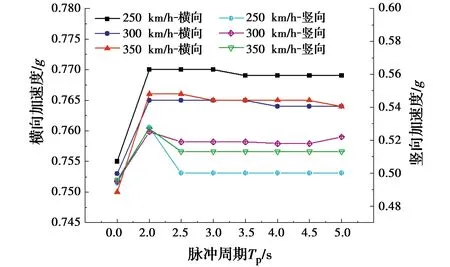
图18 桥梁跨中加速度随脉冲周期的变化

图19 脱轨系数随脉冲周期的变化
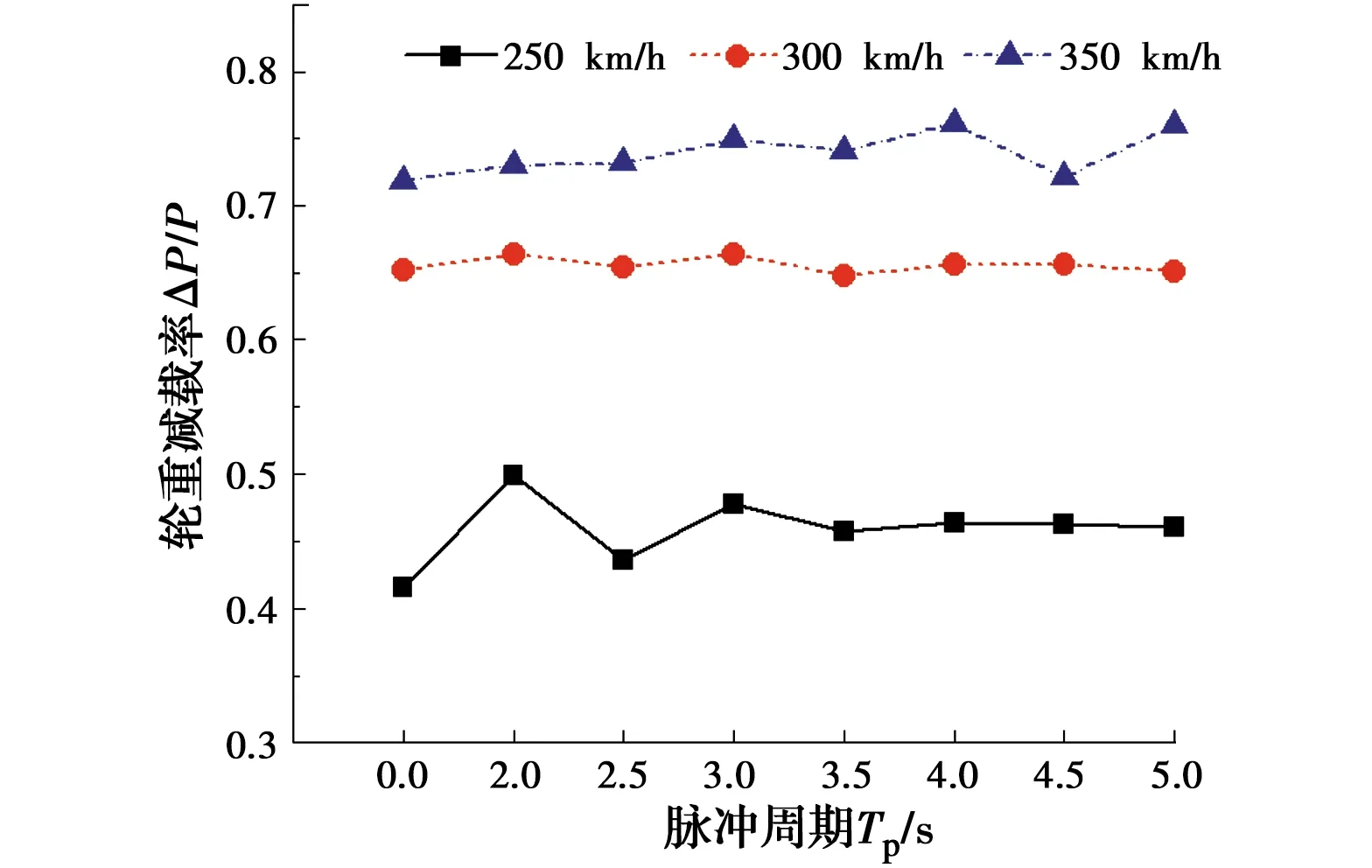
图20 轮重减载率随脉冲周期的变化
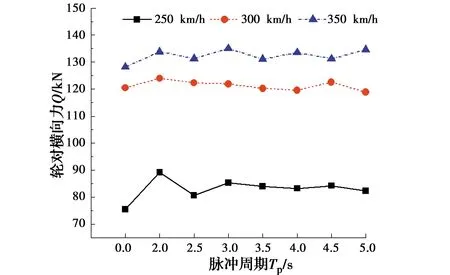
图21 轮对横向力随脉冲周期的变化
由图16~图18可得:1)脉冲周期对桥梁的位移响应影响显著。当脉冲周期由2.0 s变化至5.0 s时,桥梁的横向和竖向位移均急剧减小,但均大于远场地震动时的响应;2)相比桥梁位移,桥梁的加速度响应随脉冲周期的变化不明显,但同样均比远场地震动时大。由此说明,脉冲周期是近场地震作用下影响桥梁动力响应的重要参数,且对桥梁位移响应的影响大于桥梁加速度。
由图19~图21可得:1)不同车速下,列车的行车安全性指标随脉冲周期的增大呈减小的趋势,但变化幅度不大;2)在脉冲周期为2.0 s且车速为250 km/h时,行车安全性指标1~3相比无脉冲时的增幅最大,分别达21.6%、20.0%和18.2%。由此可见,对于高速铁路简支梁桥,列车的行车安全性指标随近场地震速度脉冲周期的变化不敏感,对于本文的计算条件,在脉冲周期为2.0 s时列车的行车安全性指标最大。
3.4 脉冲幅值的影响分析
进一步考察脉冲幅值对车桥系统动力响应的影响。保持脉冲周期为3.0 s不变,脉冲幅值依次取0.0、0.5、0.6、0.7、0.8、0.9、1.0、1.1、1.2、1.3、1.4、1.5 m/s,其中,脉冲幅值为0.0表示无脉冲。不同脉冲幅值的近场地震作用下桥梁跨中的位移和加速度响应对比分别如图22和图23所示,列车的行车安全性指标对比分别见图24~图26。
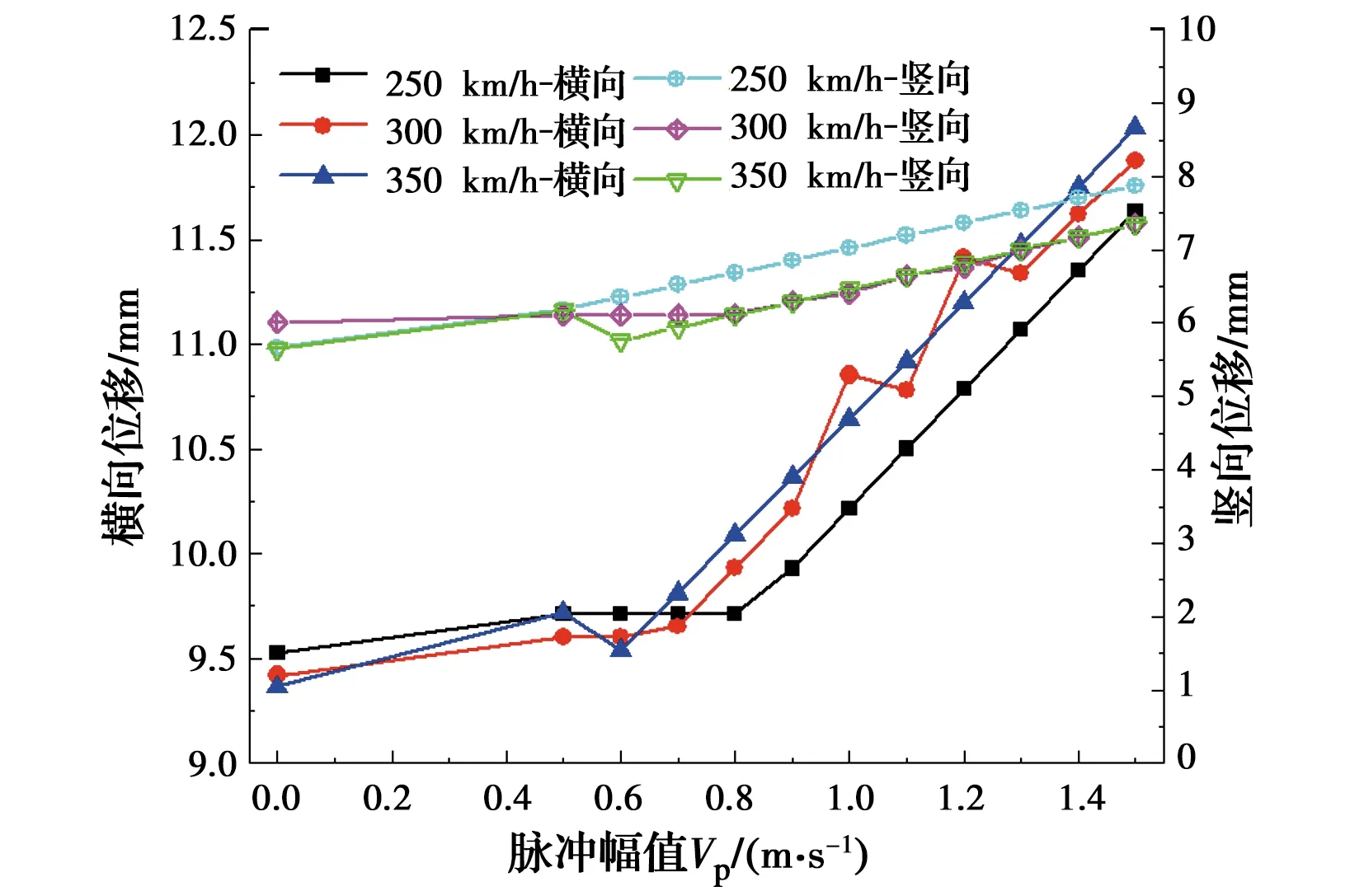
图22 桥梁跨中位移随脉冲幅值的变化
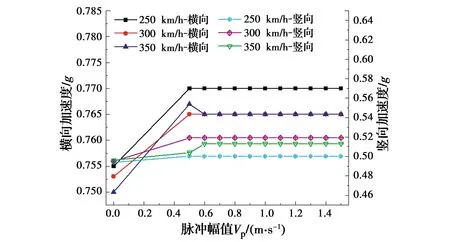
图23 桥梁跨中加速度随脉冲幅值的变化
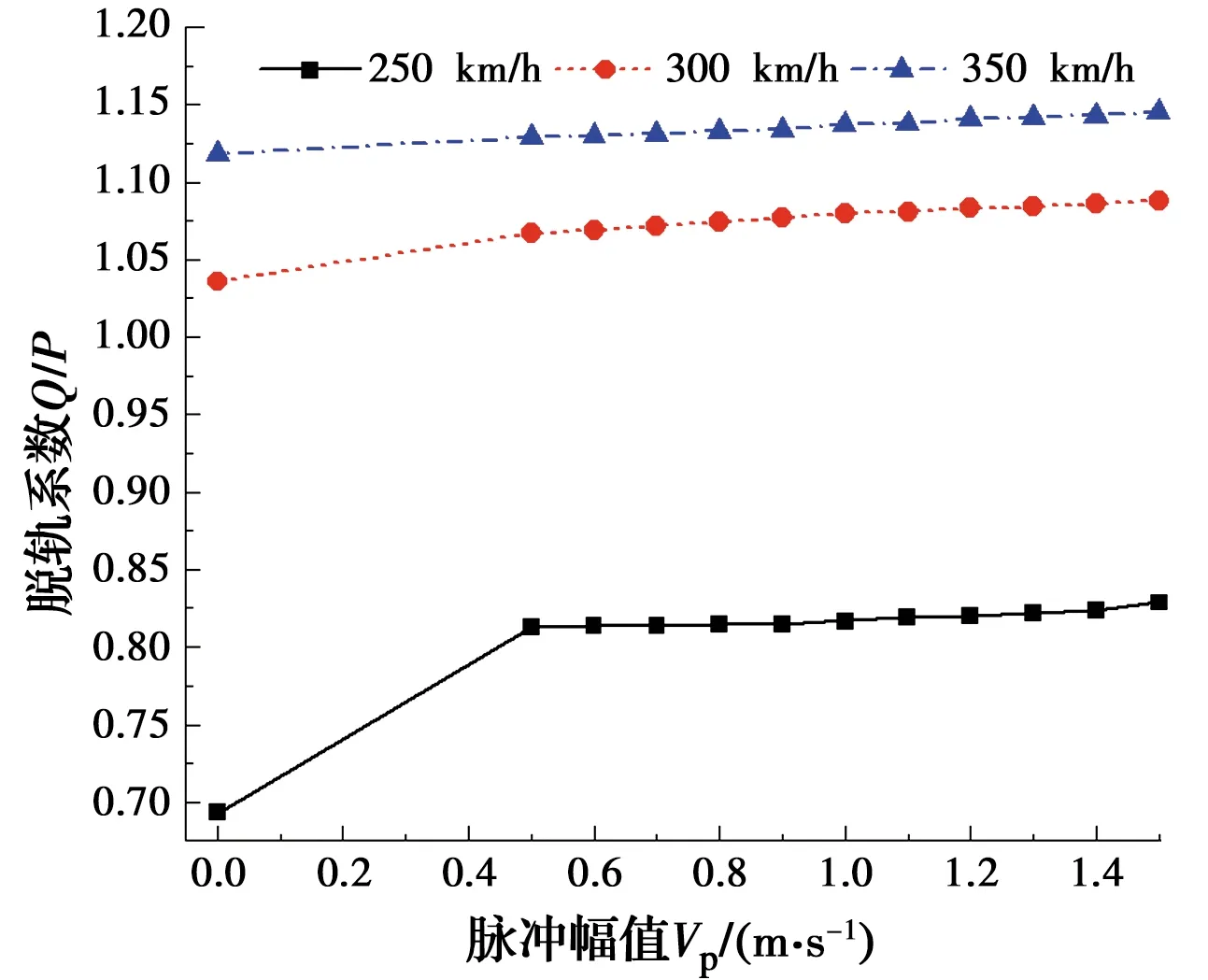
图24 脱轨系数随脉冲幅值的变化
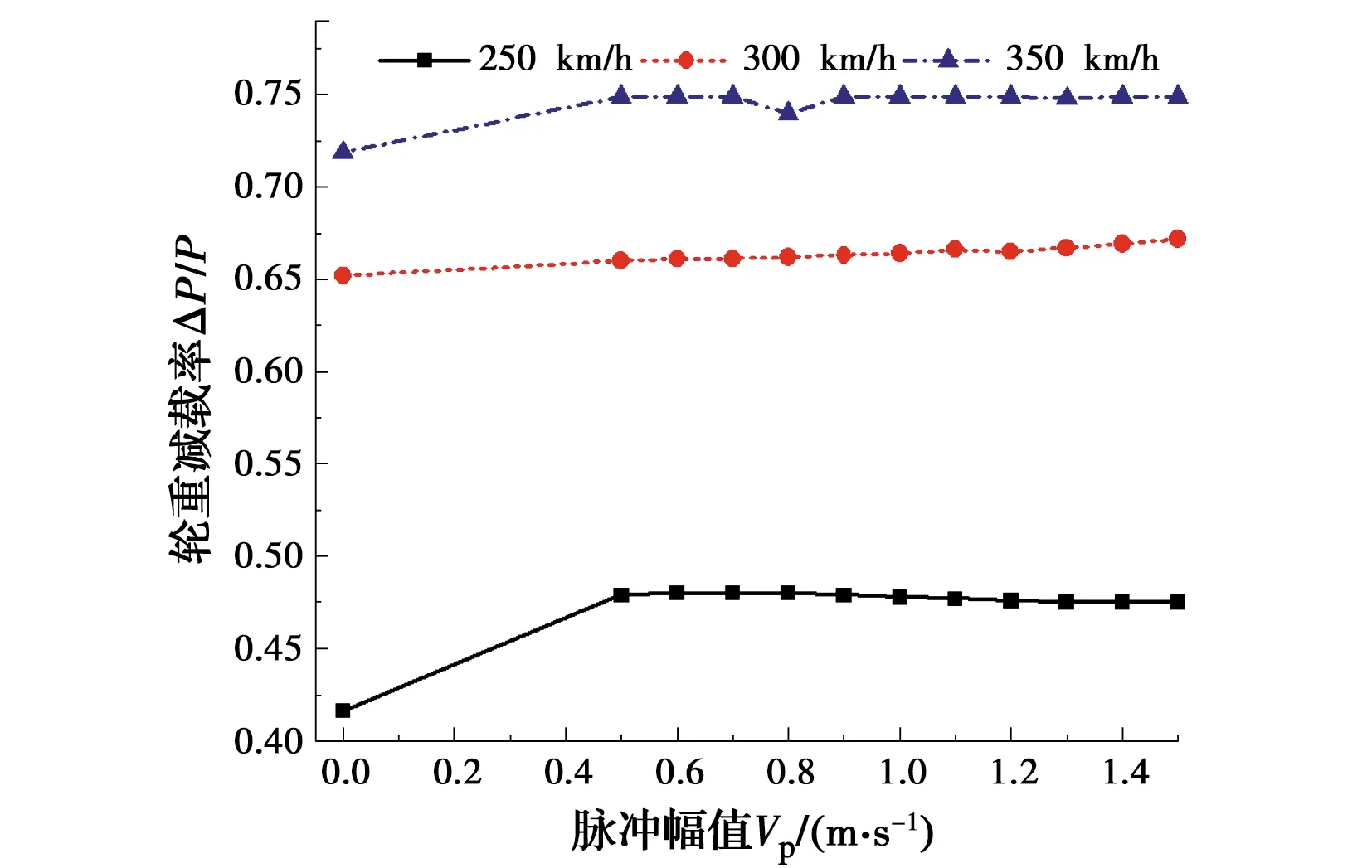
图25 轮重减载率随脉冲幅值的变化
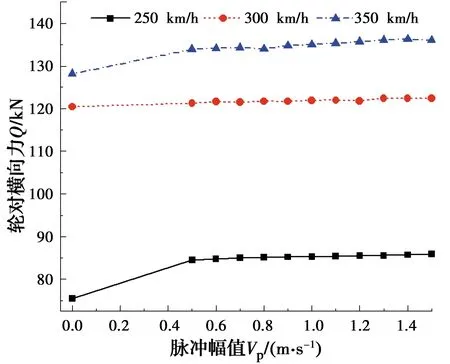
图26 轮对横向力随脉冲幅值的变化
由图22和图23可得:1)不同车速下,桥梁的横向位移和竖向位移均随脉冲幅值的增大而线性增大,且横向位移的增幅大于竖向位移;2)桥梁的加速度响应在不同脉冲幅值下相差不大。由此说明,近场地震脉冲幅值与桥梁的位移响应呈线性正相关,且对桥梁加速度的影响不明显。
由图24~图26可得:1)不同车速下,列车的3项行车安全性指标均随速度脉冲幅值的增加而增大,但增速小于桥梁位移;2)当车速为250 km/h、脉冲幅值由无脉冲变化至0.5 m/s时,指标1~3的增幅最大,分别为17.3%、15.1%和12.0%。由此可见,脉冲幅值对列车的行车安全性指标有影响,但其影响小于桥梁位移,在实际计算中可根据震级和震中距进行计算。
4 结论
基于车桥耦合振动理论,以TTBSAS程序为计算工具,通过人工合成不同参数的脉冲型近场地震动,详细探讨了脉冲类型、脉冲周期和脉冲幅值对典型高速铁路简支梁桥车桥系统动力响应的影响,得到以下主要结论:
1)近场地震速度脉冲会显著增大高速铁路简支梁桥车桥系统的动力响应,在近场区域的车桥耦合振动分析中不能忽略该速度脉冲的影响。对于本文的计算条件,当车速为250 km/h时,考虑近场地震速度脉冲时桥梁的横向、竖向位移最大增幅分别为11.5%、24.1%,列车的脱轨系数、轮重减载率和轮对横向力指标最大增幅分别为16.2%、10.8%和9.8%。
2)对于高速铁路简支梁桥,脉冲类型、脉冲周期和脉冲幅值对桥梁位移的影响远大于桥梁加速度和桥上列车的行车安全性指标,在选取近场区域的速度脉冲参数时可不考虑桥上列车的影响。
3)对于本文的计算条件,双半波脉冲和三半波脉冲近场地震作用下桥梁的动力响应幅值明显大于单半波脉冲,且当脉冲周期为2.0 s时车桥系统的动力响应最大,同时,脉冲幅值与简支梁桥的位移响应呈线性正相关。
本文仅针对近场区域高速铁路线路中应用最广泛的简支梁桥车桥系统进行了研究,近场地震速度脉冲对其他桥型的影响还有待进一步研究。
