弹性环组件刚度特性仿真与试验

□ 齐文浩 □ 常乐浩 □ 彭 智 □ 宋 文

1.长安大学道路施工技术与装备教育部重点实验室 西安 710064 2.中船重工第七○五研究所 西安 710075

1 研究背景

大多数涡轮机的转子系统在轴承支点处都设有弹性支承[1]。通过弹性支承能够降低支承刚度,从而调整和控制系统的临界转速,吸收系统中的振动能量,抑制系统的振动幅值,使转子系统平稳运行[2-3]。

弹性环组件结构简单,质量轻,可靠性高,具有良好的刚度特性,是一种最为常见的弹性支承[4-5]。研究弹性环组件的刚度特性,对转子系统在高速状态下的动态特性设计有重要意义[6-7]。

Diligenskiy等[8]通过有限元模型,分析了不同公差值对弹性环组件刚度的影响。刘闯等[9]利用有限元方法对弹性环组件的刚度进行计算,通过与理论解析法对比,验证了有限元方法的有效性,并分析了刚度对各结构参数的敏感程度。龙向阳等[10]利用有限元方法对弹性环组件刚度特性进行分析,通过试验验证了有限元方法计算的有效性,并研究了结构参数对刚度特性的影响规律。刘勇等[11]利用ANSYS Workbench软件的参数化语言,建立考虑弹性环组件接触的非线性有限元模型,分析不同结构参数对等效刚度的影响。张盼盼等[12]利用有限元方法分析了不同结构参数对弹性环组件刚度大小的影响,以及弹性环组件参数变化对转子系统临界转速的影响规律。然而,现有研究中对弹性环组件刚度的试验研究仍较少,对各参数的影响强弱程度缺乏总结。

笔者采用有限元方法对弹性环组件进行接触分析,并通过试验对比,验证分析方法的有效性。此外,还分析结构参数对刚度特性的影响,总结各参数影响的强弱程度,为弹性环组件的结构设计提供参考。

2 弹性环组件结构

笔者研究的弹性环组件材料为60Si2Mn,其弹性模量为206 GPa,泊松比为0.26。弹性环组件结构如图1所示。在弹性环组件周向的内外表面,分布有数目相同、均匀交错的内外凸台。弹性环组件主要结构参数见表1。弹性环组件在工作过程中,内凸台与衬套外环面接触,外凸台与轴承座内环面接触。弹性环组件工作状态如图2所示。

▲图1 弹性环组件结构

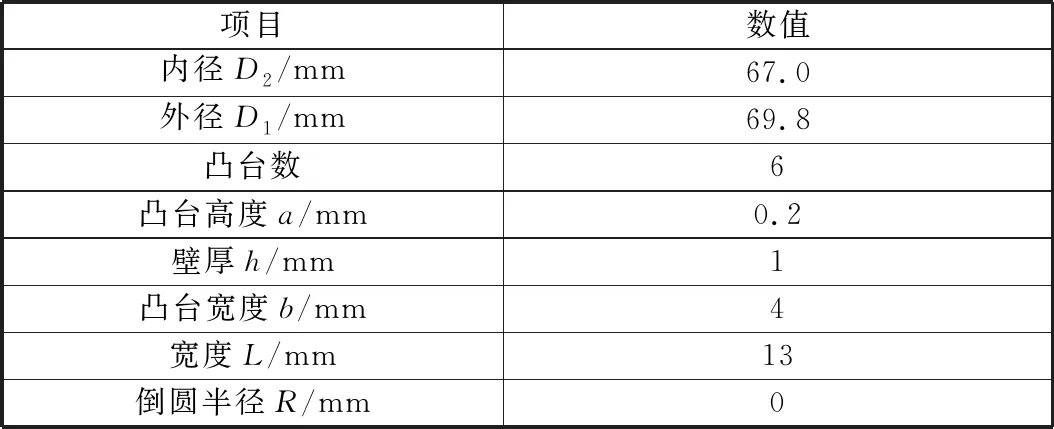
表1 弹性环组件主要结构参数

▲图2 弹性环组件工作状态

3 有限元模型

为了消除轴承刚度对弹性环组件变形的影响,在进行有限元分析时,不对轴承进行建模,仅在弹性环组件内、外两侧分别建立两个圆环,模拟衬套外环面和轴承座内环面的作用。为了降低内、外圆环变形对弹性环组件变形的影响,将其考虑为刚性结构,以获得更加准确的弹性环组件的变形量。弹性环组件实体模型如图3所示。根据弹性环组件在实际情况下的受力特点,对弹性环组件施加的边界条件如下:弹性环组件的内、外两侧分别与相邻的内、外圆环面建立接触单元,对内圆环的内径表面所有节点进行全约束,在外圆环外径表面施加Y轴负方向均布线载荷,对外圆环端面任意圆周线的轴向位移及周向位移进行约束。弹性环组件有限元网格如图4所示。

▲图3 弹性环组件实体模型

▲图4 弹性环组件有限元网格

4 刚度计算

在刚度计算过程中,通过在外圆环外径表面施加Y轴负方向均布线载荷,计算得到弹性环组件在径向的最大位移量,根据刚度定义,确定弹性环组件的刚度。当载荷取100 N时,弹性环组件的位移场如图5所示。

▲图5 弹性环组件位移场

计算弹性环组件在不同载荷下的变形情况,如图6所示。由图6可以发现,变形与载荷基本呈线性关系。通过线性拟合,得到弹性环组件的刚度为2.14×106N/m。

5 试验原理

为了验证有限元方法的有效性,对弹性环组件的刚度进行试验测量。在测量过程中,根据弹性环组件在

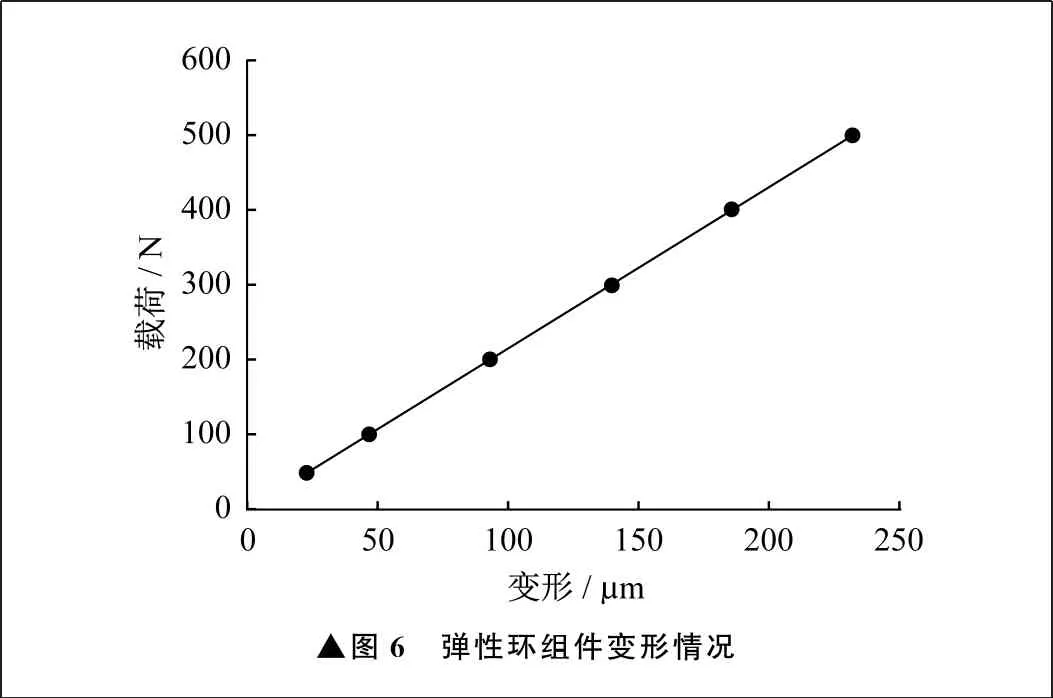
▲图6 弹性环组件变形情况

实际情况下的受力特点,设计了一套测量弹性环组件刚度特性的试验装置。试验装置结构和试验装置实物分别如图7、图8所示。

▲图7 试验装置结构▲图8 试验装置实物

弹性环组件内凸台与内圆环的外径表面相连,内圆环的内径表面通过衬套与轴相连。弹性环组件外凸台与外圆环的内径表面相连,支撑轴与支撑座相连,并且与支撑板底座的钢板用螺栓连接,通过拉伸试验机施加载荷。试验中,用电涡流位移传感器测量各载荷下弹性环组件的位移。由于两个支撑座的跨距非常小,并且支撑轴的弯曲刚度远远大于弹性环组件的刚度,因此可以将支撑轴视为刚体,弯曲变形可忽略不计,测得的位移即可认为是弹性环组件的位移。读取拉伸机测力仪上显示的载荷,根据刚度定义得到弹性环组件的刚度。

6 试验结果分析

保持弹性环组件外凸台尺寸不变,分别改变外圆环安装孔直径,得到弹性环组件外凸台与外圆环安装孔径向间隙为0、0.02 mm、0.04 mm时弹性环组件在不同载荷下的变形,依次如图9～图11所示。

▲图9 径向间隙为0时弹性环组件载荷变形曲线▲图10 径向间隙为0.02 mm时弹性环组件载荷变形曲线▲图11 径向间隙为0.04 mm时弹性环组件载荷变形曲线

径向间隙为0时为标准配合。由图9～图11可以看出,弹性环组件在加载和卸载过程中得到的载荷变形曲线不重合,并且在卸载至载荷为0时有残余变形存在,加载曲线与卸载曲线形成了明显的迟滞回线。通过反复加载和卸载,弹性环组件各次加载或卸载时的载荷变形曲线将趋于一致。在不同的径向间隙下所表现出的迟滞回线有较大差异。在径向间隙为0时,迟滞回线非常明显。随着径向间隙的增大,迟滞回线逐渐减弱,加载和卸载时的曲线接近重合。当载荷增大至一定程度后,弹性环组件将达到变形极限。随着载荷不断增大,弹性环组件变形增大幅值很小,并且随着径向间隙的增大,弹性环组件的变形极限逐渐增大。利用图9～图11载荷变形曲线,取其中的稳定加载区域,通过线性拟合计算得到每次加载时的刚度,最后取平均值,得到弹性环组件的刚度。弹性环组件刚度试验结果见表2。由表2可知,随着径向间隙的增大,弹性环组件的刚度会呈现出非线性减小,并且径向间隙越大,刚度减小的幅度越小。

表2 弹性环组件刚度试验结果

7 试验与仿真对比

有限元计算的弹性环组件变形与试验中第一次加载测得的弹性环组件变形结果对比如图12所示。标准配合时通过有限元仿真得到的弹性环组件刚度为2.14×106N/m,试验结果为2.07×106N/m,试验所得刚度略小于仿真结果。这是由于进行有限元分析时,将弹性环组件内外圆环视为刚体,系统变形仅包含弹性环组件的变形。而在试验时,所测得的变形除包含弹性环组件变形外,还包含内外圆环、支撑轴的变形,以及安装间隙等,所以变形略大于弹性环组件自身的变形,换算得到的弹性环组件刚度略小于实际值。用有限元分析方法计算出的弹性环组件刚度与试验结果相差仅为3.4%,具有较高精度。由此,后续在研究结构参数对弹性环组件刚度的影响时,均采用有限元方法进行计算。

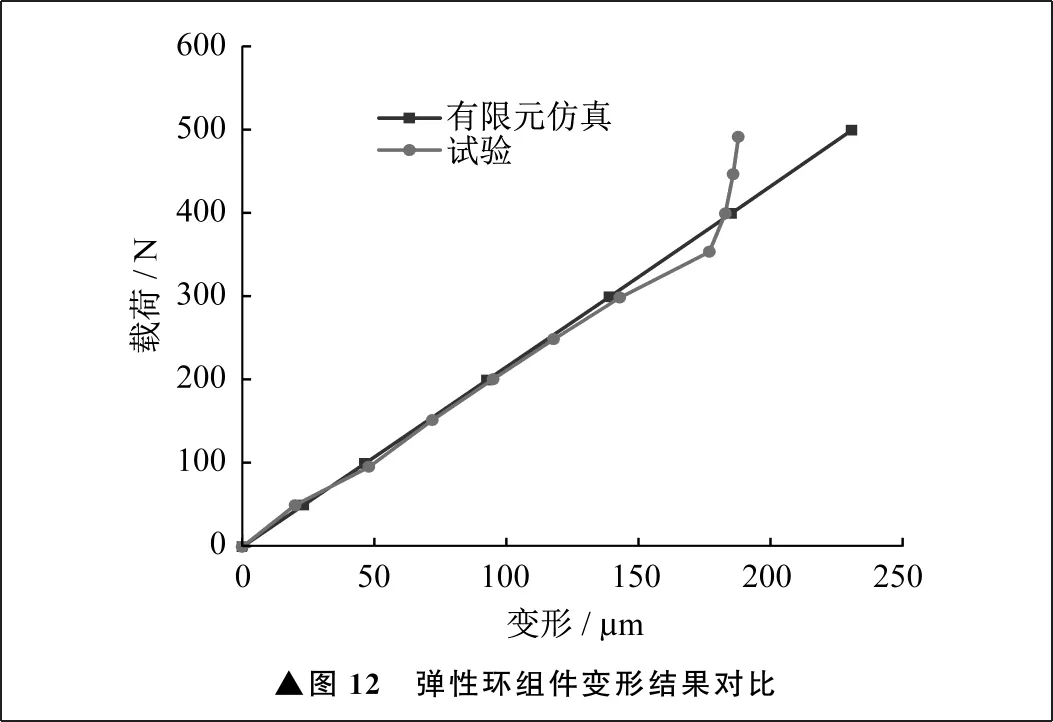
▲图12 弹性环组件变形结果对比

8 结构参数对弹性环组件刚度影响

以原弹性环组件为基准,运用所建立的计算模型,研究不同结构参数对弹性环组件刚度的影响规律,以及影响的程度。

8.1 凸台数量

仅改变凸台数量,其余结构参数不变,得到凸台数量对弹性环组件刚度的影响曲线,如图13所示。由图13可知,弹性环组件刚度随着凸台数量的增加逐渐增大。这是由于弹性环组件的每个环段可以简化为两端固支的梁,中间受到集中载荷的作用,当凸台数量增多时,环段变短,刚度会增大,并且凸台数量越多,刚度增大的速度越快,呈现非线性变化趋势。

▲图13 凸台数量对弹性环组件刚度影响曲线

8.2 凸台宽度

仅改变凸台宽度,其余结构参数不变,得到凸台宽度对弹性环组件刚度的影响曲线,如图14所示。由图14可知,随着凸台宽度的增大,弹性环组件刚度逐渐增大。这是由于凸台宽度增大时,凸台宽度在每个环段所占的比例增大,因此刚度会增大,并且基本呈线性变化趋势。凸台宽度每增大1 mm,刚度约增大0.3×106N/m。

▲图14 凸台宽度对弹性环组件刚度影响曲线

8.3 凸台高度

仅改变凸台高度及内外径,其余结构参数不变,得到凸台高度对弹性环组件刚度的影响曲线,如图15所示。由图15可知,弹性环组件刚度随着凸台高度的增大逐渐增大。这是由于增大凸台高度,相当于局部增大了弹性环组件的壁厚,因此刚度会略有增大,并且基本呈线性变化趋势。凸台高度每增大0.1 mm,刚度约增大0.1×106N/m。

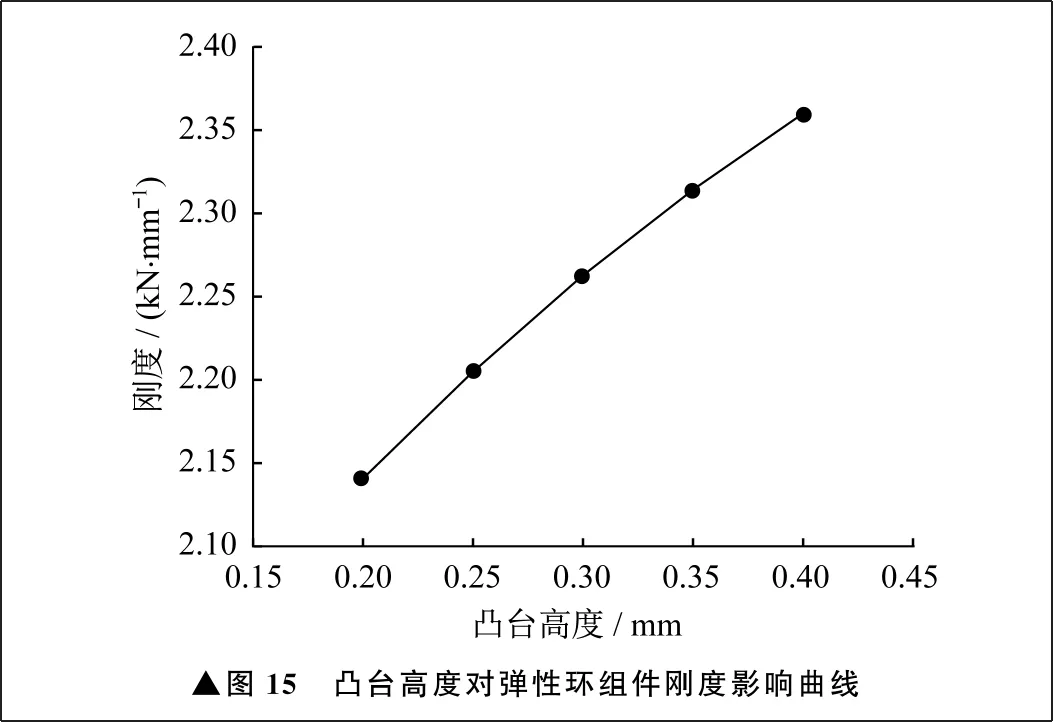
▲图15 凸台高度对弹性环组件刚度影响曲线

8.4 圆角半径

仅改变圆角半径,其余结构参数不变,得到圆角半径对弹性环组件刚度的影响曲线,如图16所示。由图16可知,随着圆角半径的增大,弹性环组件刚度逐渐增大。这是由于增大圆角半径,相当于局部增大弹性环组件的壁厚,因此刚度会略有增大,并且基本呈线性变化趋势。当圆角半径从3 mm增大到11 mm时,刚度仅增大3.9%。

8.5 壁厚

仅改变壁厚及内径,其余结构参数不变,得到壁厚对弹性环组件刚度的影响曲线,如图17所示。由图17可知,弹性环组件刚度随着壁厚的增大逐渐增大。这是由于随着壁厚的增大,弹性环组件环段的截面惯性矩增大,因此刚度会增大,并且呈现出非线性增大的变化趋势。当壁厚从1 mm增大到1.8 mm时,刚度增大了441.2%。

▲图16 圆角半径对弹性环组件刚度影响曲线

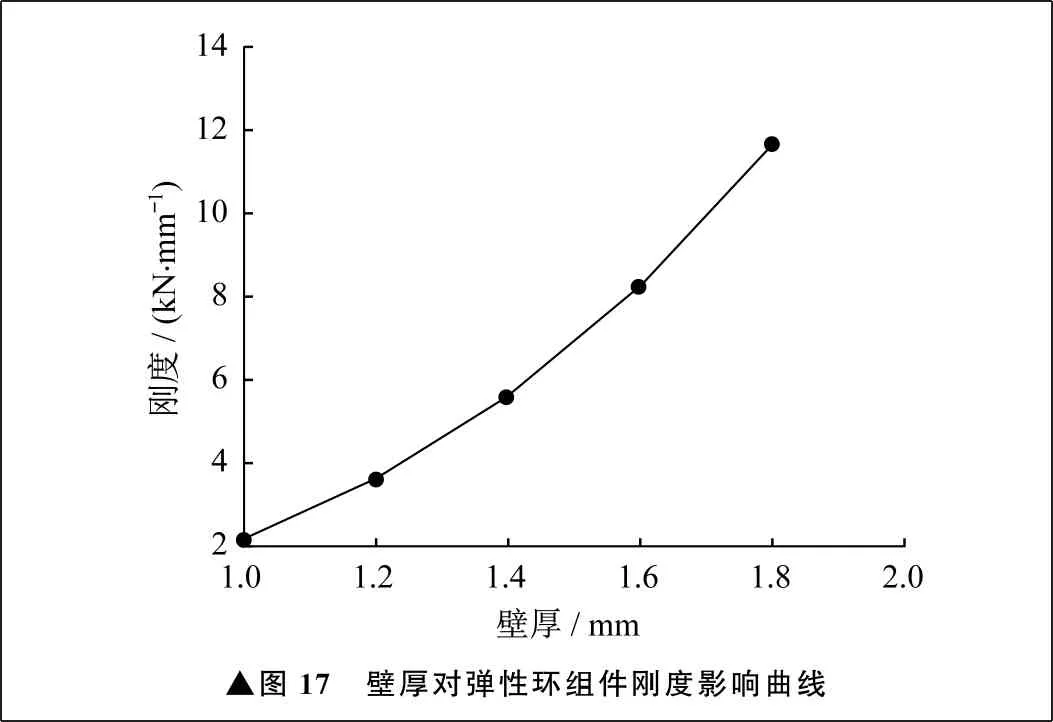
▲图17 壁厚对弹性环组件刚度影响曲线

8.6 轴向宽度

仅改变轴向宽度,其余结构参数不变,得到轴向宽度对弹性环组件刚度的影响曲线,如图18所示。由图18可知,弹性环组件刚度随着轴向宽度的增大逐渐增大。这是由于随着轴向宽度的增大,弹性环组件环段的截面惯性矩增大,因此刚度会增大,并且基本呈线性变化趋势。轴向宽度每增大1 mm,刚度约增大0.17×106N/m。

8.7 内外径

以内径为例,仅改变内径,其余结构参数不变,得到内径对弹性环组件刚度的影响曲线,如图19所示。由图19可知,弹性环组件刚度随着内径的增大逐渐减小,外径同理。这是由于内、外径增大,使弹性环组件环段变长,因此刚度会减小,并且基本呈线性变化趋势。内径每增大1 mm,刚度约减小0.09×106N/m。

9 结束语

笔者采用有限元方法对弹性环组件进行接触分析,换算得到弹性环组件的刚度。通过试验分析了弹性环组件的迟滞回线现象,以及径向间隙对弹性环组件刚度特性的影响。随着径向间隙的增大,弹性环组件的迟滞回线现象逐渐减弱,弹性环组件刚度逐渐减小。将试验结果与仿真结果进行对比,验证了有限元方法的有效性。基于有限元方法,分析了不同结构参数对弹性环组件刚度的影响规律。结果表明,随着凸台数量、壁厚、凸台宽度、凸台高度、圆角半径、轴向宽度的增大,弹性环组件的刚度会有所增大;而随着内、外径的增大,弹性环组件的刚度会有所减小。不同结构参数对弹性环组件刚度影响的程度从强到弱依次为凸台数量、壁厚、凸台宽度、轴向宽度、凸台高度、内外径、圆角半径。

▲图18 轴向宽度对弹性环组件刚度影响曲线▲图19 内径对弹性环组件刚度影响曲线