在实践中反思 在反思中优化
——以“环形跑道问题”为例
2022-02-23陆祥雪吴秋芳
■陆祥雪 吴秋芳
知识与能力是教师专业发展的两个方面。知识主要包括教育知识和学科知识两个方面,这两个方面融合为一体形成学科教学知识(简称PCK)。顾泠沅先生认为教学案例是发展PCK的重要载体。为了探求环形跑道问题中的相等关系,笔者先组织学生模拟跑,再用几何画板模拟实验。通过不断优化,发展了教师的教学能力,促进了教师的专业发展。
一、教学实施
问题1:运动场环形跑道周长400m,小红跑步的速度是爷爷的倍,他们从同一起点沿跑道的同一方向同时出发,5min后小红第一次与爷爷相遇。请问:小红和爷爷跑步的速度各是多少?
这是苏科版《数学》七年级上册“用一元一次方程解决问题”中的问题4。教材在分析中直接给出这个问题的数量关系式:小红跑的路程-爷爷跑的路程=400。
那么,教师在授课时,怎么来阐述这个相等关系呢?
师:这个问题中的相等关系是什么呢?
生1:第一次相遇时,小红比爷爷多跑一圈。
师:你是怎么知道的?
(学生1沉默。)
师:好!为了验证这位同学所说的相等关系,我们用几何画板做个模拟实验。如图1,我们用实心点表示小红,空心点表示爷爷,为了方便区分,我们将小红与爷爷的同一跑道,分离为两个同心圆,不过我们认为它们的半径是相同的。图中的“动画点”就相当于小红与爷爷起跑的“发令枪”,我只要一点击,两个点就运动起来了。现在我开始点击“动画点”,请同学们注意观察小红比爷爷多跑了多少?
在学生观看两个点的运动的同时,教师手握鼠标,当实心点与空心点第一次相遇,再次点击“动画点”停止运动(如图2)。
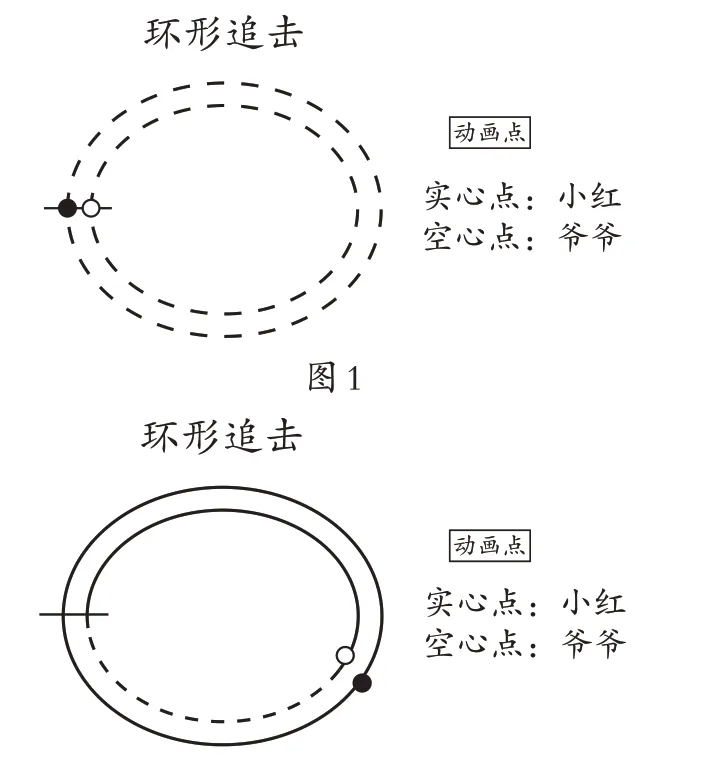
图2
师:好!我们现在停止运动,请问,小红与爷爷第一次相遇时,小红比爷爷多跑了多少?
生1:多跑了一圈。
师:你是怎么知道的?
(学生1还是沉默。)
师:我们重新演示一遍。
师:当实心点(小红)再次回到起点时(如图3)(此时教师点击“动画点”按钮,使两点运动停止),此时实心点(小红)已经跑了多少?
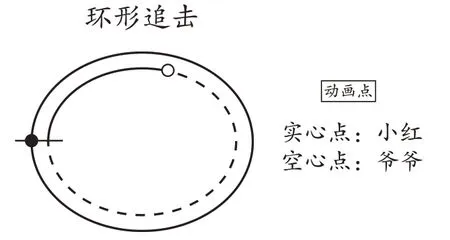
图3
生1:一圈。
师:当实心点(小红)第一次与空心点(爷爷)相遇时,小红比爷爷多跑了多少?
生1:还是一圈。
师:请你解释一下原因。
生1:因为从小红再回到起点到追上爷爷(第一次相遇),小红与爷爷跑的路程是相同的,而在此之前,小红已经跑了一圈,所以小红比爷爷多跑了一圈。
师:很好!那就请你到黑板上来完整地解答这个问题。
师:接下来我们再看一下这道题的变式题。如图4,小明与小华在一个边长为100米的正方形ABCD的跑道上练习跑步,小明的速度为每分钟200米,小华的速度为每分钟150米,小明、小华分别从A、B两点同时出发,按顺时针方向跑。请问:当小明和小华首次相遇时,此题的相等关系又是什么?
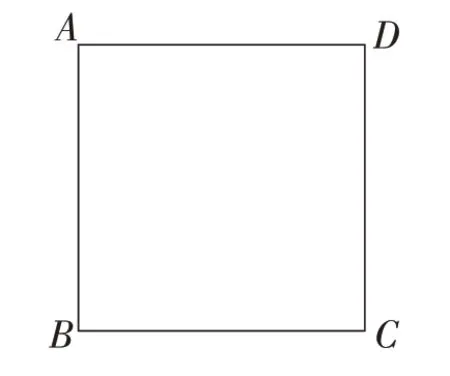
图4
生2:小明比小华多跑了300米。
师:为什么?
生2:小明跑到小华的起点B时,小明跑了300米,当小明首次与小华相遇时,小明比小华多跑了300米。
师:同意的请举手。
二、教学改进
起初,设计教学方案时,为了寻找相等关系,教师请两名学生到讲台来,站在同一个位置。一名学生扮演“小红”,另一名学生扮演“爷爷”,沿教室内的过道,来模拟跑。教师提醒学生注意观察小红比爷爷多跑了多少。于是,两名学生在教室内跑了起来。教师问:“小红是不是比爷爷多跑了一圈?”有学生说“是的”,但大多数学生不发声。教师发现回答的人很少,就觉得可能有学生没有看清,于是,又重新演示了一遍。当教师再次提问时,学生的回答还是很少,说明大多数学生没有看清问题中的相等关系。
设计模拟跑的目的是用实际情境帮助学生寻找问题中的相等关系,提升学生的参与度,提高学习兴趣。但学生并没有通过这个模拟跑的实验发现问题中的相等关系。另外,教师在学生没有办法说明“小红比爷爷多跑一圈”的情况下,也没有帮助学生解决这个疑惑,而是选择避而不谈。笔者对此教学设计进行反思,问题出在何处?在教室里模拟跑,学生的注意力仅是集中在两个学生身上,而不能观察到两个学生的行进路径。找到问题的症结,笔者做出几点改进。
改进的目标是化不可视的行进路径为可视。于是,有了两个改进的方案:一是用线示法,将小红与爷爷跑的路线画出来,如图5,让学生直观地比较小红比爷爷多跑了多少。在起点与相遇点之间,小红与爷爷有一段路程是一样的,如果我们把它们擦除,剩下的部分恰好是一圈。二是用几何画板来进行模拟实验,这样小红与爷爷跑的路径可视性更强,且不需要场地。
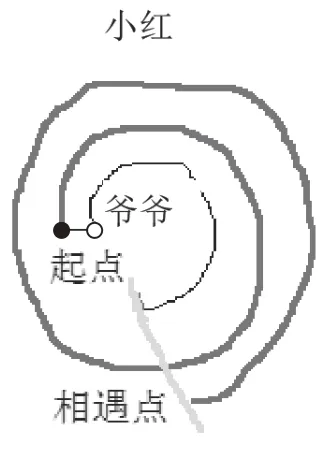
图5
三、教学反思
从最初设计到优化后的最终设计,经历了“设计—实施—反思—改进”的循环过程,这个过程不但提高了课堂教学效率,而且促进了教师自身发展。
1.“设计—改进”促进终身学习。
在“环形跑道问题”中,学生不能探索出相等关系,所以需要改进设计,打破原有的知识、思维框架,否则只能墨守成规,不断退步。
现代教育技术已经得到了很大的发展,虽然知识是古老而陈旧的,但借助新技术,知识以新的面貌呈现。其实,只要用几何画板的动态演示就能解决这个问题。利用软件对动点的追踪功能,学生可以很全面地从整体上观察两人的跑步路径,而不是在教室或操场上只能看到局部的情形。这就是PCK分类中的一类,即将特定的学习内容呈现给学生的策略知识。
2.“设计—改进”促进深度思考。
利用几何画板让学生直观地观察小红比爷爷多跑了一圈,但学生受路径重叠的影响,效果反而不如图5的“线示法”。学生在解决变式题时受挫,这都促使我们去反思,去进行更深度的思考,触及问题的本质,由教师的深度思考去引导学生的深度学习。其实,这个模拟实验,让我们从直观上获得了感性知识,同时,还体现数学的理性特点。怎么说明这个从实验中获得的相等关系?这就需要教师在备课时做充分思考。我们为什么要从运动过程中抽出图3,而不是仅仅出现起点与终点的图1或图2,目的就是为进行理性的解释铺路。当小红再回到起点时,她已经跑了一圈,小红从现在到与爷爷第一次相遇,两人所跑的路程相同,所以小红比爷爷多跑了一圈。根据学生回答的情况,可以多次重复演示,并在小红回到起点时停留,让学生观察,找准观察的对象。这实际上就是基于同一个起点,如何比较小红和爷爷所跑路程的长短问题。学生在明晰这点之后,就可以扔掉“直观”的拐杖,解决相关的变式题。实践证明,教师利用改进优化后的方案实施教学,学生解答变式题的准确率提高很多。
3.“设计—改进”促进“四个理解”。
章建跃博士提出“理解数学、理解学生、理解技术、理解教学”。我们要充分掌握这四个“理解”间的关系,恰当地使用信息技术帮助学生理解数学内容。信息技术起辅助作用,还得结合学生的想象力。对七年级学生来说,形象思维占主导地位,所以我们通过几何画板来直观、整体地呈现小红及爷爷跑的过程,有助于学生突破难点,理解相等关系。教师应树立终身学习的理念,与时俱进,只有常备一桶活水,方能浇灌新时代的花朵。
