数形结合 提升数学学习力

□ 南京师范大学附属中学仙林学校小学部南邮校区 袁 琳

一、联系实物，体会数理内涵

数形结合中的“形”可以理解为实物、模型图、线段图、数轴、直角坐标系等，其中实物演示也是帮助学生理解抽象的数学原理、直观认识数学事物的一种重要方式。教师要遵循学生的认知规律，通过引入生活中常见的实物模型，让学生通过数学概念的现实原型来理解抽象知识，逐步建立理性认识。

例如，以数轴概念的讲解来说，教师可以展示马路的图片，或让学生画一条马路，要求图片中含有杨树、柳树、电线杆、站牌等物体，让学生思考：问题1：马路可以用什么几何图形表示？问题2：站牌在马路中起到什么作用?问题3：你是怎么确定各物体的位置的？以此来引导学生学会用直线、点、方向、距离等几何符号进行画图，表示实际问题。接着，教师和学生一起在黑板上采用正负数、几何符号、方向等知识将树、电线杆与汽车站牌的相对位置关系画出来，并强调0表示基准点、数的符号的实际意义是方向等知识点。有了这个铺垫之后，教师可让学生对照观察温度计的实物或观察教材图片，结合黑板上马路的图示分析温度计的结构，0℃是温度的基准点，有正负两个方向，这样让学生提前感受原点、单位长度、方向这三要素。最后再引出数轴的定义和讲解，在数学中，可以用一条直线上的点表示数，这条直线叫做数轴，原点、正方向、单位长度为数轴的三要素，以此来帮助学生深刻认识到数轴这个概念。

二、绘制导图，厘清相互关系

思维导图是表达发散性思维的有效图形思维工具，它应用到数学教学中可以帮助学生借助思维导图的结构框架来深入挖掘知识点的内涵，思考和总结相关知识点间的联系，在此基础上调动大脑思维，建立系统的知识网络体系，促使学生形成系统的学习和思维的习惯。

例如，以“图形的认识”作为统领概念，教师可以引导学生通过绘制思维导图的方式来对小学数学中关于图形的知识点进行一次系统的梳理与总结。教师引导学生独立完成平面图形、立体图形这两个大框架的完善与填充。在学生完成的思维导图中，平面图形选取了三角形、四边形、圆三个方向，又将四边形细化为学过的长方形、正方形、平行四边形、梯形等，补充了其定义、性质、周长及面积公式的知识点。立体图形以球、圆柱圆锥、长方体正方体为三级结构，并在思维导图中绘制了各立方体的模型，加入了表面积、体积公式的知识点。整体来看结构清晰，内容丰富，完成的较为成功。

也就是说，绘制思维导图的过程就是知识整合的过程，它更顺应我们大脑的思维模式，将思维导图引入小学数学教学中，可以为学生提供有效的思考框架，记录和引导学生的思维过程，通过数与形的结合帮助学生巩固和记忆数学知识，效果较好，是教师可以关注的教学方向。

三、借助数轴，发展逻辑思维

数轴是学习数学一个非常重要的工具。在小学阶段，学生第一次接触数轴这个概念，教师可以将数轴的学习与小学数学中的加减法、分数、负数等知识点联系起来，引导学生通过数轴的图示来理解数学知识，感受数形结合思想，促进学生的抽象思维能力及逻辑推理能力的共同发展。

例如，题目是这样的：在数轴上，如果点a表示的数是-2，那么到点a距离3个单位的点所表示的数是______。我们就需要用到数形结合思想来分析问题。首先画出数轴，具体步骤包括画一条直线、选取原点、正方向、规定单位长度，接下来在数轴上用短竖标出刻度，数轴下标出数值。接着对照题意，找到a所表示的数-2，要求的数到点2的距离是3，结合数轴可以发现这个数既可以在a的左侧，也可以在a的后侧，分别是-1和5。这道题的易错点是在数轴上距离已知点n个单位长度的点有两个，分别位于已知点的两侧，学生很容易忽略其中的一个点导致错误。但只有学生养成数形结合的良好思维习惯，借助数轴图来思考和分析问题，就可以尽可能避免这类错误，提高答题正确率。

学生运用数形结合思想解题的关键就是能够建立数与形的联系，而数轴本身就是数与形结合的有力工具。作为小学数学教师，不仅要带领学生认识和理解数轴的定义及其性质，建立起数的位置感和秩序感，还要善于将数轴与其他数学知识点及题目联系起来，引导学生体会数形结合的数学思想方法。

四、动手操作，发展空间想象

如果说联系实物、创设情境是为学生学习数学概念提供感性材料支持，帮助学生获得感性认识的话，教师还要在此基础上进一步借助多种表征活动让概念表象操作化与活动化，让学生通过动手操作和观察思考来经历知识的形成过程，真正理解数学事物的本质和规律，加速学生的认知进程。

以一道数学题目为例：小明将一张正方形纸对折两次，如图所示，在中央点打孔后再将它展开，展开后的图形是（ ）。

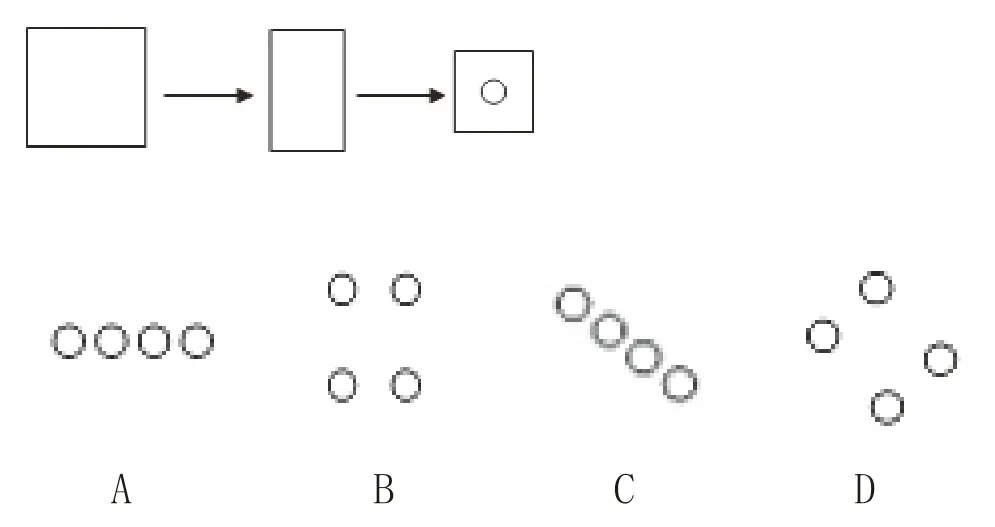
这道题对学生的空间想象能力要求较高，首先一张正方形纸对折两次，平均分成4份，每一份上都有一个小圆圈，可以排除A、C，到这一步大部分学生都没有问题。但究竟展开之后是B还是D的形状，一些学生在脑海中建构不出对折展开之后的图形变化，感到难度很大。那么，教师可以让学生准备一张正方形纸，依据题意将纸对折两次，在中间减去一个圆形后再展开，这时候通过动手操作学生就可以确定正确答案为B，并通过操作过程更加直观地观察到了图形的变化，我们是沿着正方形的两边对折的，不是沿对角线对折的，所以最后展开后的图形不会沿对角线成轴对称。就这样，学生利用动手实践的方式直观清晰地感受到数与形的结合与相互转化，有效促进了空间想象能力的发展，课堂教学较为成功。

五、建构模型，快速解决问题

数学模型可以理解为用数学语言去认识现实世界，解决实际问题，是沟通数学与现实世界的桥梁。教师在开展教学时要善于结合数学知识来设计生活实践类问题，让学生通过习题训练来理解生活中的数学现象，学会构建及应用数学模型巧解问题，提升学生学以致用的能力。

例如，题目是这样的：某小学五年级学生参加运动会，此次运动会有跑步和篮球两个项目，报名跑步的有31人，报名篮球的有15人，两个项目都报名的有8人，全班共50人，没有报名运动会项目的有多少人？这个题是一道生活实际类问题，但很多学生不知道如何列式进行计算，教师就可以引入韦恩图来帮助学生理解与建构这类型题目的解题模型。韦恩图是用来展示不同数据集合之间的关系，集合通常用圆来表示，如在这道题目中，我们把报名跑步和报名篮球的圆圈连在一起，重叠部分就是两个项目都报名的8人。根据图示就可以找到题目中这些数据的对应关系，要想求出没有报名的学生有多少人，需用50-（31+15-8）=12（人），由此便可顺利地解决这类型题目，帮助学生总结应用韦恩图模型来解决此类型问题的基本思路，教学效果较好。

也就是说，建构数学模型的方式可以帮助学生更加系统地去梳理数形结合思想所适用的题目类型，并在这个过程中去归纳和总结解题的技巧与方法，达到优化解题途径、提升解题效率的效果。同时，在数学教学中渗透数形结合思想不仅局限于文中提到的联系实物、绘制导图、借助数轴、动手操作及建构模型这几个方向，其更多可行性与实践策略还有待教师继续去思考与探索。

总而言之，数形结合思想的实质是将抽象的数学语言与直观的图像语言结合起来，关键是要让学生理解代数问题与图形之间相互转化的基本逻辑，能够根据数与形之间的对应关系，通过数与形的相互转化来解决数学问题。作为小学数学教师，不仅要重视数学基础知识与基本技能的传授，还要关注学生数学思维的发展与思想方法的培养，这样才能真正帮助学生提升良好的数学解题能力与学习能力，建构起高品质的小学数学课堂。