超大跨度扁平地下洞室变形控制标准研究

陶连金， 黄琳昆， 石 城， 张乃嘉

(北京工业大学 城市与工程安全减灾教育部重点实验室， 北京 100124)

0 引言

随着经济、国防等事业的发展，国内大型地下洞室工程发展迅速[1]，断面形式逐渐向大跨度、大断面方向发展。根据地下洞室“轴比论”和新奥法支护原理[2]，地下洞室在设计时需满足一定的矢跨比要求。在不良围岩或不利地应力条件下，大跨度洞室需通过增大断面高度以维持自身稳定[3]，造成空间浪费，增加成本；而在良好围岩条件下，地下洞室可建设成超大跨度、小矢跨比结构型式，极大地节省施工成本，提高空间利用率，因此，超大跨度扁平地下洞室应运而生[4]。

在施工过程中，围岩变形便于监测，制定围岩变形控制标准是地下工程施工安全的必要条件。全球首例超大跨度洞室结构——挪威Gjøvik的奥运场馆跨度62 m，高度25 m，开挖变形在7～8 mm[5]。我国大型地下工程中，水电厂房起步较早，结构型式以大断面、高边墙为主： 锦屏Ⅰ级水电站[6]主厂房孔口累计位移11.57 mm，主变室监测点最大位移191.73 mm；双江口水电站[7]主厂房第1层开挖后各监测点4 mm以内变形占比84.6%，最大变形14.4 mm；后子岩水电站[8]开挖变形达到50 mm，超过国内相同规模水电站施工变形的平均水平。我国首例大跨度扁平隧道——韩家岭隧道最大变形28 mm；规模最大的地下轨道交通工程——京张高铁八达岭车站[9]大跨段监测变形最大值19 mm。总体来看，各工程案例变形量各异，且数值较发散。

目前，国内外对于隧道变形控制标准进行了规定，如我国2005版《铁路隧道设计规范》、日本《NATM设计施工指南》等，但主要是基于断面跨度小于16 m的情况制定的，对于超大跨度扁平洞室尚缺乏明确的变形控制标准。随着越来越多大跨扁平洞室投入建设，建立其变形控制标准对洞室的设计和施工具有重要意义。

本文结合某超大跨度扁平地下洞室，对洞室变形控制标准进行研究。以岩体强度作为评判指标，通过建立洞室沉降变形与围岩极限应变的关系，计算大跨扁平洞室在不同围岩条件下的变形控制极限值。本文的研究成果以期为类似工程的设计和施工提供参考。

1 超大跨度洞室变形控制标准

1.1 岩体强度与极限应变

地下岩石工程中常以岩石强度特性作为围岩稳定性评价指标。地下洞室开挖导致围岩应力重分布，当洞周切向应力超过岩体单轴抗压强度，则认为岩体发生破坏。Aydan提出以岩体极限应变εcr作为量化围岩挤压程度的指标，即当洞室围岩应变水平小于此值时，可以在无支护条件下维持自身稳定；超过该极限值，就有可能发生挤压性问题或者围岩失稳[10]。Sakurai、Hoek、Barla等学者先后将岩体极限应变应用于隧道施工安全等级的评定，相比于采用应力指标，围岩极限应变更有利于工程监测和变形计算，而且地下洞室失稳与岩体应变直接相关[11]。

本节介绍目前应用较为广泛的几种岩体极限应变的公式，计算大跨洞室的极限应变。

1.1.1 Sakurai法

Sakurai[12]提出岩体极限应变计算公式如下：

(1)

式中：σcm为岩体单轴抗压强度；Em为岩体弹性模量。

由于原位岩体压缩试验通常难以进行，Sakurai公式的取值相对麻烦，工程实践中常以工程岩体分类法反映岩体的工程特征。目前，Barton提出的Q值分类法考虑的地质因素较全面，是目前应用范围较广的分类方法，Singh法和Barton法均是在Sakurai法和Q分类法基础上的改进。

1.1.2 Singh法

Bhasin等[13]提出岩体强度σcm由完整岩石的单轴抗压强度和岩体分类共同决定，并提出基于Q分类的σcm经验公式(2)。Singh等[14]通过对若干工程实例岩体数据的整理，指出式(2)适用于坚硬岩和完整岩体，即Q>10、σci>100 MPa的岩体。对于Q<10、σci>2 MPa的岩体，Singh等学者提出修正公式(3)。

(2)

σcm=7γQ1/3，Q<10。

(3)

式(2)—(3)中：γ为岩体容重；Q为Barton岩体质量指标；σci为完整岩石单轴抗压强度。

结合Singh等[15]所建立的完整岩石和节理岩体的强度特性关系公式(4)，可得到Singh法计算的岩体极限应变εcr,见式(5)。

(4)

(5)

式中Ei为完整岩石弹性模量。

1.1.3 Barton法

Barton[16]对大量工程岩体数据进行分析，提出Em经验公式。

(6)

结合式(1)和式(4)，得到εcr计算公式。

(7)

1.1.4 Hoek经验法

Hoek等[17]基于大量工程实践，认为岩体极限应变εcr与σcm/p0相关，提出经验公式如下：

(8)

式中：p0为岩体初始应力水平；pi为支护结构上的围岩压力。

该公式适用于隧道半径为4～16 m、岩石单轴抗压强度为1～30 MPa、地质力学强度指标为10～35的围岩。

1.1.5 极限应变计算结果

这些年，但凡我每次从老家回来，母亲看我坐定，总是先详细询问我老家的枣树、院落、房屋的情况，听到枣树垂暮、满院荒草、屋顶渐漏，她常常深叹一口气，幽幽地说：“啥时候能把房子拾掇拾掇，让我再回去住几天，看看枣树、浇浇水，就好了。”可是，老家终究是没人住的，拾掇了也无用，荒了几十年，连水电都没有了，母亲看似简单的要求，却终难实现。

由于大跨扁平洞室的尺寸(大于50 m)和围岩条件，Hoek经验法不再适用；岩体质量Q值分类法已成功应用于挪威Gjøvik的奥运场馆超大跨洞室工程案例。因此，本节分别采用Singh法和Barton法计算围岩极限应变，岩石力学参数引自文献[18]，计算结果如表1所示。由表可知,Singh法和Barton法计算结果较为接近，本文采用偏于保守的Barton法计算结果。

表1 岩体极限应变

1.2 围岩临界变形

本节通过建立洞室沉降量与围岩应变的关系，确定大跨洞室变形控制标准[19]。

图1 洞室拱顶沉降计算模型

文献[5]中数值模型计算结果洞室变形以拱顶沉降为主，拱顶沉降占洞室高度比例为0.34%，水平收敛占洞室跨度比例为0.006 4%，水平收敛对洞室变形影响较小。因此，立足于简化模型原则，假设洞室侧墙为刚性。

定义α为洞室矢跨比，则

(9)

由几何关系可得：

(10)

洞室沉降变形后的半径和矢跨比分别为：

(11)

(12)

洞室沉降引起的围岩环向应变

(13)

据上述公式，计算出50、60、70 m跨度洞室(矢跨比为0.19)拱顶沉降与围岩应变关系，见表2。

表2 围岩应变与拱顶沉降关系

(14)

将式(12)中沉降量S提到等号左边得到式(15)，可见沉降量S与洞室跨度b成正比。因此，S-ε关系式可表示为式(16)，其中k与洞室矢跨比α有关。

S=b(α-α′)。

(15)

S=bkε。

(16)

采用上述方法计算不同矢跨比洞室的S-ε关系，计算结果如表3所示。

表3 矢跨比α与参数k关系

经数据拟合得到参数k与矢跨比α关系式如下：

(17)

1.3 洞室变形控制标准

由式(16)可知，大跨洞室拱顶沉降量与跨度成正比。本节提出沉降跨度比S/b作为大跨扁平洞室沉降变形控制标准：

(18)

式中： SF为安全系数，参考TB 10003—2016《铁路隧道设计规范》[20]中混凝土强度安全系数取值，围岩的安全系数取3.0。

针对本文中矢跨比为0.19的大跨洞室，结合表1中岩体极限应变值，计算出洞室沉降跨度比S/b如表4所示。

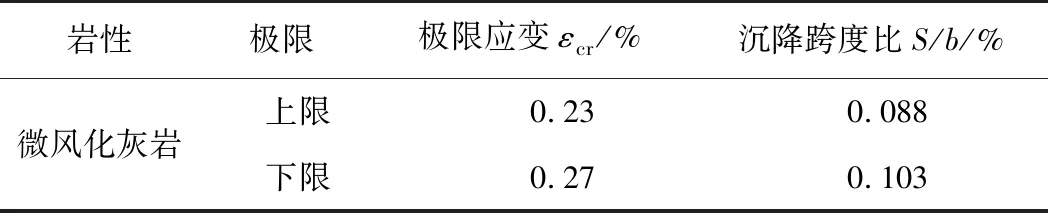
表4 超大跨度扁平洞室变形控制标准

施工过程中，为保证支护结构和作业人员安全，建立变形监控数据分级管理机制[21]，如表5所示。

表5 大跨洞室沉降变形分级管理

2 分部施工变形分析

2.1 大跨扁平洞室施工方案

某超大跨度扁平地下洞室，跨度66 m，断面高度18 m，矢跨比为0.19，高跨比为0.28，如图2所示。洞室形状扁平，长度大于100 m，最大埋深120 m。

图2 开挖步序图 (单位： m)

工程区以厚—巨厚层的白云质灰岩、灰岩为主，岩体完整坚硬致密、强度高，抗风化能力强，岩石单轴抗压强度高于95 MPa。主洞室层理不发育，且多为整体块状结构，产状稳定，结构面粗糙，总体以Ⅱ级围岩为主，Q值大于10。

超大跨度扁平地下洞室虽具有良好的围岩条件，但由于跨度大、断面面积大，无法采用全断面法、台阶法等传统开挖方案[22-23]。本工程采用“分部开挖-预留岩柱”方法进行施工，如图2所示。具体开挖方案如下：

1)开挖中间导洞Ⅰ;

2)采用台阶法开挖侧导洞Ⅱ和Ⅲ，上台阶与导洞Ⅰ错距约10 m；

3)洞室通长范围内的导洞Ⅰ、Ⅱ、Ⅲ开挖完成后逐步开挖岩柱Ⅳ；

4)开挖大台阶岩块Ⅴ。

据上述开挖方案，可将整体开挖过程分为2个阶段：

1)小导洞阶段，包括前2个施工阶段，在拆除预留岩柱Ⅳ之前，该洞室开挖区域为1个中间导洞和2个侧导洞。

2)大跨洞室阶段，包括拆除岩柱Ⅳ和开挖台阶岩块Ⅴ。

2.2 施工变形分析

在小导洞阶段，各导洞跨度相对较小，与一般隧道尺寸接近，施工技术相对成熟，加之围岩条件良好，因此推断该阶段围岩变形较小。考虑到邻近3个导洞相互影响，根据文献[24]提出的双隧普氏拱理论，计算得预留岩柱Ⅳ的宽度大于各导洞间形成联合拱的临界宽度，可认为各导洞上方地压力拱相互独立。综上，在小导洞阶段围岩变形控制标准可参照TB 10003—2005《铁路隧道设计规范》。

在大跨洞室阶段，随着岩柱Ⅳ的开挖，各小导洞联通形成超大跨度洞室，围岩应力重分布导致洞室拱顶必将产生较大沉降变形[25]，大跨洞室阶段宜采用前节所述的基于岩体极限应变的大跨洞室变形控制标准。

3 计算方案

本节通过建立2D有限元模型计算大跨扁平洞室分部开挖引起的围岩变形，并与所建立的变形控制标准进行对比。

3.1 数值模型

考虑到研究对象的对称性，选取模型一半进行计算，如图3所示。洞室跨度66 m，断面高度18 m，埋深60 m，详细几何参数如图2所示。经试算，模型侧边界取2倍洞室跨度可消除边界条件对模型开挖的影响，模型尺寸为165 m×120 m。模型边界条件设置为底部完全固定，两侧约束法向自由度，顶部为自由面。

3.2 材料模型参数

假设岩体为连续均匀介质，采用6节点平面应变单元模拟，服从Mohr-Coulomb强度破坏准则，岩体弹性模量采用式(6)计算，并参考《工程岩体规范》中围岩力学参数建议值范围，具体参数如表6所示。支护措施仅考虑250 mm厚CF30混凝土，采用线弹性模型，梁单元模拟，材料参数按照JG/T 472—2015《钢纤维混凝土标准规范》；初期支护与围岩之间的相互作用采用界面单元模拟，刚性连接，材料属性与围岩相同。

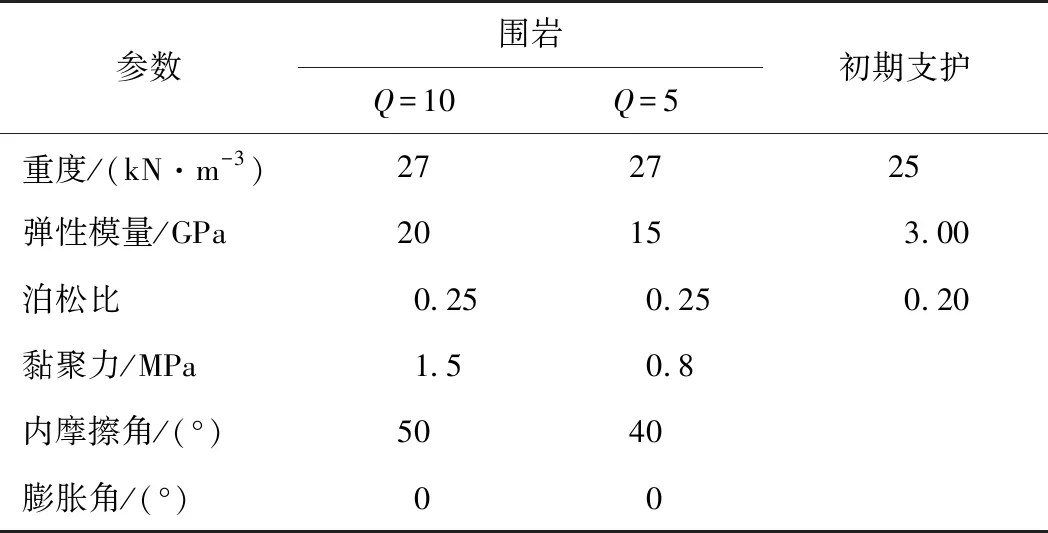
表6 材料模型参数

根据超大跨度地下洞室成洞条件，岩体初始地应力状态对地下洞室稳定性影响显著[26]，大跨洞室选址中应充分考虑地应力条件，选择利于大跨洞室成洞的地应力环境。本文所依托工程案例，侧压力系数为1.66～2.53。本节假定计算模型中初始地应力均匀分布，2个主应力分别为水平方向和竖直方向，采用式(19)和式(20)计算，λ为侧压力系数(保守起见，本节计算中λ取1.0)。

σy=γH。

(19)

σx=λσy。

(20)

3.3 计算结果

围岩条件Q=10工况下，各监测点沉降值随开挖步的变化曲线如图4所示，围岩各开挖阶段竖向变形云图如图5所示。由图4和图5可知，小导洞阶段，围岩沉降变形很小，中间导洞最大沉降1.50 mm，侧导洞最大沉降1.70 mm，均低于TB 10003—2005《铁路隧道设计规范》中Ⅱ级围岩双线隧道拱顶相对下沉临界值0.03%～0.06%。

图4 施工监测点变形曲线 (Q=10)

大跨洞室阶段，围岩沉降明显增大，拆除岩柱阶段拱顶沉降量占最终变形的78.8%，体现预留岩柱对洞室稳定的重要性；拆除岩柱阶段，拱顶沉降7.02 mm，开挖大台阶后洞顶沉降6.99 mm，体现了开挖卸载效应。大台阶岩块Ⅴ开挖前后围岩变形云图相近，说明开挖大台阶岩块Ⅴ对洞室变形影响较小，该规律与文献[27]中结论一致。

3.4 结果分析

数值监测结果与控制标准对比见表7。由表7可知，在围岩条件Q=5、Q=10情况下，大跨洞室沉降变形很小，均满足变形控制标准，且低于Ⅱ级预警值，证明了在良好围岩条件下修建大跨扁平洞室的可行性。参考类似工程案例实测变形量(见表8)，Gjøvik奥运场馆最终变形在8 mm以内，因此，在大跨洞室修建过程中应加强监测，严格控制变形，充分发挥围岩自身良好的承载能力，保证洞室稳定。

图5 分部开挖竖直方向变形云图 (Q=10) (单位： mm)

表7 数值监测结果与控制标准对比

表8 工程案例对比

4 结论与建议

1) 超大跨度扁平地下洞室拱顶沉降极限值与洞室几何形状、围岩强度特性相关，本文提出以“沉降跨度比”作为大跨洞室沉降变形总体控制标准，并建立沉降变形分级管理办法。

2) 超大跨度扁平洞室采用“分部开挖-预留岩柱”开挖方法，将开挖过程分为小导洞阶段和大跨洞室阶段，围岩变形主要发生在后一阶段。小导洞阶段洞室沉降标准宜采用现有规范，大跨洞室阶段宜采用本文所述的基于岩体极限应变的大跨洞室变形控制标准。

3) 结合数值计算结果以及挪威Gjøvik工程案例实测围岩变形可知，大跨洞室修建过程中应严格控制围岩变形，满足控制标准，保证洞室稳定。

4) 大跨洞室的支护措施如喷锚支护、预应力锚索支护等对控制洞室变形起到重要作用，建议在后续工作中分析考虑支护措施下的大跨洞室变形控制标准。