负极性方波下介质阻挡对电晕放电重复率的影响

2022-02-22付淦郑重

广东电力 2022年1期

付淦, 郑重

(华北电力大学，北京 102206)

电晕放电产生的空间电荷积聚于电气设备固体绝缘表面，造成局部电场畸变并逐渐破坏其绝缘性能；另一方面，电晕放电作为产生低温等离子体的常用手段，在工业应用中提供绝缘介质表面所需的电荷，如有机污染处理、静电分离器、静电印刷等[1-2]。

电极被绝缘介质分隔的情况下发生的电晕放电又称介质阻挡电晕放电(dielectric barrier corona discharge，DBCD)[3-7]。电气设备附近发生电晕放电所产生的空间电荷在电场力作用下向绝缘表面聚集，造成绝缘附近电场畸变，甚至超过限值[8]；尤其在单极性电压下，电场方向恒定，绝缘表面电荷的积聚现象更为严重。有研究表明，表面电荷的积累是导致绝缘表面沿面闪络的一个重要原因[9]。目前，关于介质阻挡下表面电荷的研究主要集中在3个方面：表面电荷的积聚特性[10-11]、表面电荷的消散特性[12-13]、表面电荷积聚对闪络电压的影响[14-15]，而关于介质阻挡表面电荷积聚对放电重复率影响的研究很少。放电重复率是分析电晕放电特性的一个重要指标[16]。研究不同介质阻挡情况下的电晕放电重复率有利于了解DBCD机理，还能反映表面电荷积聚对放电重复率的影响。为了改善材料的绝缘特性，增强电器设备绝缘的安全性，有必要对介质阻挡下的电晕放电重复率进行研究。

为了进一步研究DBCD下电荷的积聚与消散的微观物理过程，以及其对电晕放电的影响，本文采用典型针板电晕放电模型，对多种片状绝缘材料以及一种FEP (fluorinated ethylene propylene，全氟乙烯丙烯共聚物)绝缘电缆施加负极性周期脉冲方波，记录放电起始前8个周期下的DBCD次数，分析电压与放电次数的数值关系，对不同介质阻挡对放电次数和放电重复率的影响和相关规律进行研究。

1 实验

1.1 局部放电测量系统

局部放电测量系统由惠普33120A函数/随意波形发生器、TREK 20/20C高压发生器、ICM局部放电系统、耦合电容、测量阻抗、横滨DL750示波记录仪、高压探头、GPIB传输线组成，如图1所示。

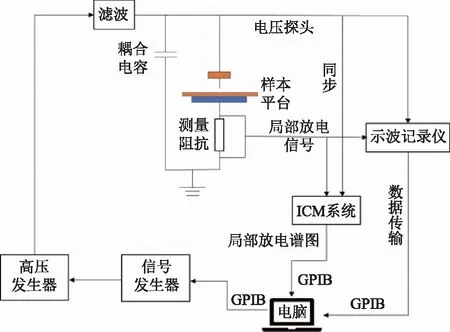
图1 局部放电测量分析系统结构

通过GPIB缆线将编辑的波形传至惠普33120A函数/随意波形发生器，向高压发生器发送指定脉冲信号；高压发生器对输入信号放大2 000倍，最大输出电压为±20 kV DC/20 kV AC；耦合电容值为50 nF，并与高速火花保护间隙并联；测量阻抗由1 kΩ电阻和火花间隙并联制成；局部放电信号通过测量阻抗，经过同步后传输至ICM局部放电系统，并在配套软件上形成相应的时/频域局部放电谱图；横滨DL750示波记录仪具有12 bit的A/D分辨率，最高107s-1的采样频率，最大2.5×108的单次采样数量和最长记录时间30 d，能长时间对局部放电过程进行记录和采样；高压探头是德国PMK PPE 20kV高压探头，比率为1 000∶1，最大承受14 kV AC和20 kV DC以及40 kV电压脉冲；函数/随意波形发生器、电脑处理器和DL750示波记录仪通过GPIB缆线进行交互，实现波形的控制和数据的传输。

1.2 实验平台与波形

实验平台为针-板阻挡电晕放电模型，如图2所示。

图2 电晕放电针-板模型

实验平台由针-板电极以及片状绝缘材料组成，针电极长30 mm，尖端半径为50 μm，材料为不锈钢；平板电极直径80 mm，厚10 mm，材料为黄铜；两电极间距为10 mm；同时，厚1 mm、长100 mm、宽100 mm的绝缘材料覆盖于平板电极之上。

电压波形采用负极性周期脉冲方波，如图3所示。

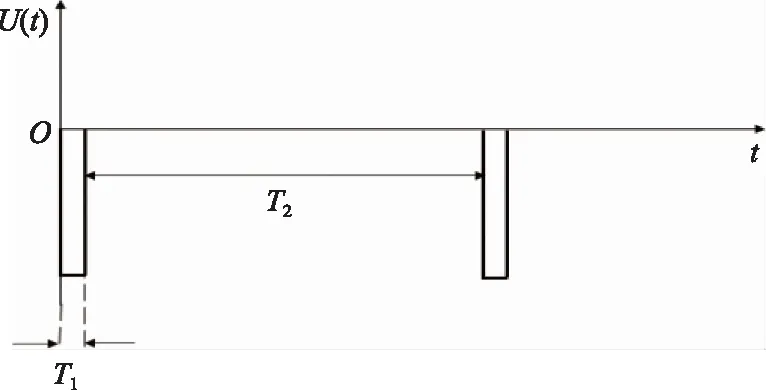
图3 负极性脉冲方波波形示意图

电压波形分为两部分：第一部分为持续时间T1=100 ms的负极性脉冲方波；第二部分为等待恢复时间T2=10 s的负极性脉冲方波，是脉冲持续时间的100倍。电荷在T2阶段消散，消散程度取决于绝缘介质表面电荷的迁移速率，并体现在各周期放电次数和放电重复率的差异上。通过比较电荷消散程度与脉冲周期可以得出电荷消散的时间常数量级。

采用负极性电压是因为负极性相比于正极性更容易起晕，并且负极性下的电晕放电规律性更强，放电幅值更加稳定[17]。本文提到的所有电压均为负极性电压。

利用示波记录仪记录不同绝缘材料在各周期T1阶段的放电次数据，通过分析放电重复率的变化规律可以反映出不同介质阻挡对电晕放电行为的影响。进行脉冲序列分析时，仅需对每次局部放电对应的时间点和放电幅值进行分析，所以在对数据进一步分析之前，要将原始数据中的局部放电点滤除，尤其要将噪声信号滤除，本文通过MATLAB程序设置幅值阈值滤除噪声信号，并利用脉冲间隔阈值滤除因为采样频率高导致的同一放电信号上多余的采样点。

1.3 数学模型

在针-板电极模型中，利用经验公式对电晕放电的电压、电流关系进行描述，随着电压的升高，电流也以某种规律上升[18-19]：

I=K1U(U-U0),

(1)

或

I=K2(U-U0)n.

(2)

式(1)—(2)中：U、I分别为施加的电压(V)、电晕放电电流(A)；U0为局部放电起始电压(partial discharge inception voltage, PDIV)；K1、K2为取决于几何结构的常数；n为相应的最优指数，与针尖半径和极间距有关。对于负极性电压和针尖半径很小的针电极来说，式 (2) 具有更好的适应性，且在针尖半径为5 μm时取n=1.6[18]。对于无绝缘介质阻挡下的电晕放电来说，常认为单次电晕放电不具有电荷积累效应，基本不会影响整个空间的电场强度，可以认为无介质阻挡时每一次电晕放电具有近似相等的电荷量q0[20]，则总的放电量

Q(t)=q0N(t).

(3)

式中N(t)为关于时间t的放电次数。瞬时放电电流

(4)

介质阻挡下每一次电晕放电都会产生一定数量的电荷数，意味着每次电晕放电都会有一定数量的电荷在绝缘表面积聚，导致表面产生一个逐渐增加的反向电势Ub，从而减弱针尖电极与绝缘材料间空气间隙的电场强度，此时式 (2) 可写成

I=K2(U-Ub-U0)1.6.

(5)

绝缘材料的表面电势Ub会随放电次数的增多而增加，放电电流I会因此减小，若Ub足够大，I可能降为0，从而停止放电。通过分析电流、电压和放电次数的关系，可以进一步了解电晕放电现象本质，也可以对放电重复率N(t)/t进行分析。

2 无介质阻挡时的电晕放电

作为设置的对照组，在研究绝缘材料对电晕过程造成的影响之前，先对无绝缘材料覆盖的情况进行分析。

无绝缘材料覆盖时的PDIV约为2.5 kV，分别施加3 kV、4 kV、5 kV电压时的第1个周期的放电次数N(t)与时间t的关系如图4所示。其中横坐标的t表示脉冲电压的作用时间，对应图3中的T1阶段。各电压水平下的局部放电次数N(t)随时间呈线性增加，说明电晕放电在对应的电压水平下具有稳定的放电重复率dN(t)/dt。

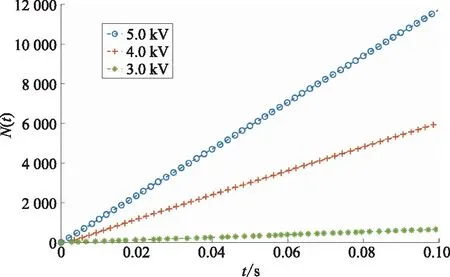
图4 无介质阻挡时分别施加3、4、5 kV时的第1个周期放电次数与时间的关系

施加5 kV电压时前8个周期T1阶段的局部放电次数N(t)与时间t的对应关系如图5所示，图中，C1—C8表示连续的8个周期。由图5可以看出，前8个周期的局部放电次数N(t)有相同的增长曲线，说明上一周期的放电不会对下一周期的放电重复率产生影响。不难理解，电晕放电产生的电荷通过黄铜电极迅速导向接地极，几乎没有电荷积累，从而每一周期的每一次局部放电状态都与初始状态相同。

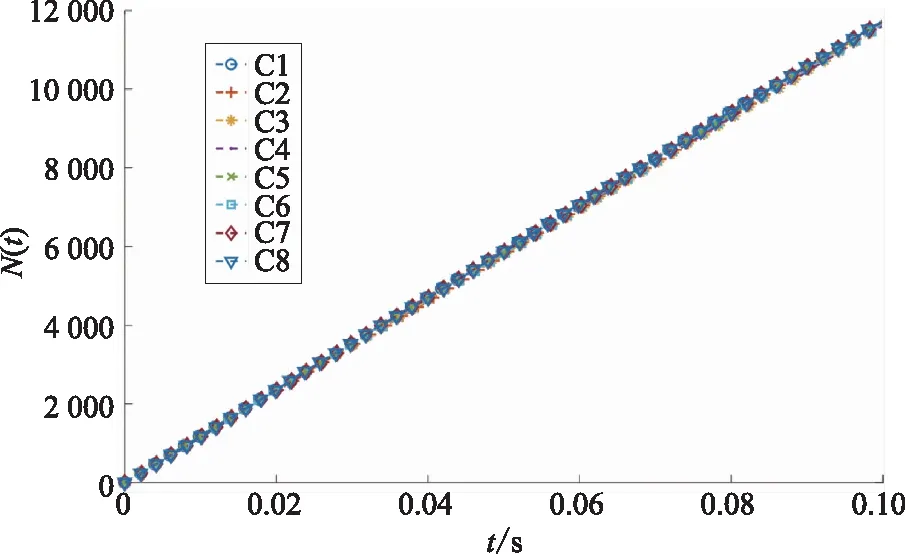
图5 5 kV下无介质阻挡时前8周期局部放电次数N(t)与时间t的关系

可以进一步推导1.3节提到的经验公式，由式 (2) 和 (4) 可以推出

dN(t)=K2(U-U0)1.6dt/q0.

(6)

无绝缘材料覆盖模型的局部放电次数N(t)与时间t为线性关系，从而T1阶段的总放电次数

N(T1)=K2(U-U0)1.6T1/q0.

(7)

式中q0为在该模型下的单次电晕放电量，约为45 pC，该值由安捷伦DSO-X 2014A示波器测得，该示波器具有最高2 ×109s-1的采样率。每次测量前使用局部放电校准仪对系统进行校准。将图4中各电压水平下的总放电次数代入式 (7) 中，可解出U0=2.64 kV，K2=2.21×10-11C/(V2·s)。

3 介质阻挡下的电晕放电

针尖处的空气发生电离产生空间电荷，空间电荷受电场作用向平板电极方向移动，在绝缘介质表面积聚并形成反向电势阻碍后续放电[21-22]。

为了进一步分析绝缘材料阻挡对电晕放电重复率的影响，本节描述不同绝缘材料覆盖于黄铜接地极板时对电晕放电的影响，与第2章无介质阻挡时的结果进行比较，可以直观反映不同绝缘材料表面的电荷积聚对电晕放电重复率的影响。

3.1 各种介质阻挡下的放电情况

实验平台与第2章相同，如图2所示。使用的绝缘材料尺寸均为100 mm×100 mm×1 mm的薄片样本，包括聚乙烯(PE)、聚碳酸酯 (PC)、聚四氟乙烯(PTFE)、聚氯乙烯(PVC)和层压纸板，各种材料的基本性质见表1。

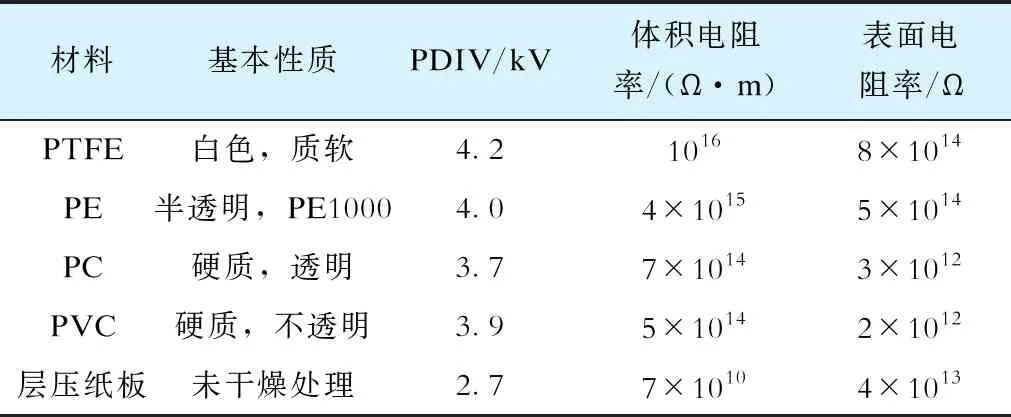
表1 各种材料的物理性质

材料的表面电阻率和体积电阻率往往对表面电荷消散有很大的影响，主要原因是基于不同的电荷消散路径[23]。表面电荷处于气-固交界区域，电荷向空气中弥散或被附近空气中的电荷中和的过程往往受表面电阻率影响较大[24]；而电荷沿着气-固交界的法相方向穿透绝缘材料注入下方的黄铜电极这一过程，亦即电荷注入过程，则受材料体积电阻率影响更大[25]。

将5种绝缘材料分为3类(①高表面电阻率、高体积电阻率的PE、PTFE；②较低表面电阻率、较高体积电阻率的PVC、PC；③较高表面电阻率、低体积电阻率的层压纸板)进行比较，进而分析不同电荷消散方式对放电重复率的影响。

表面电阻率为实验室测量值。测量方法为：将材料置于Keithley 6105阻抗适配器中，选择相应插口，施加固定数值的直流电压，Keithley 6514静电计测量电流，示波器和高压探头测量实际电压，通过电压与电流即可计算出材料表面电阻率和体积电阻率。

其中，除了层压纸板的PDIV较低，仅略高于无介质阻挡时的情况，其他4种绝缘材料的PDIV均在4 kV左右。实验环境为23.7 ℃、大气压99.72 kPa和空气相对湿度18.9% 。为了产生稳定的电晕放电，对各类材料施加约1.6倍PDIV(6.4 kV)的脉冲电压，并对各类绝缘材料进行放电起始前8周期的局部放电测量，结果如图6所示。由图6可以看出，不同于无介质阻挡时放电次数随时间线性增长，介质阻挡下电晕放电次数均具有负指数型增加趋势。

图6 不同绝缘材料6.4 kV下前8周期放电次数N(t)与时间t的关系及各周期放电次数曲线

这一负指数分布现象在放电起始的第1周期最为明显，原因是持续放电后在表面积聚的大量电荷会在绝缘表面建立较大的反向电势Ub，从而减弱了后续的局部放电活动，表现为放电重复率逐渐下降。

从图6还可以看出，除层压纸板外，各种绝缘介质的放电次数逐周期递减，并趋于饱和。根据上文基于表面电阻率和体积电阻率对5种绝缘介质的分类，结合图6(f) 可看出，5种材料各周期的放电次数也分为3块区域：区域一材料为高表面电阻率和体积电阻率的PE和PTFE，其起始周期放电次数少、放电次数稳定值低；区域二材料为较低表面电阻率和较高体积电阻率的PC和PVC，其起始周期放电次数更多，稳定值更高；区域三材料为较高表面电阻率和低体积电阻率的层压纸板，初始周期放电次数最大且各周期放电次数近似相等。区域一和二对比，说明在电荷难以注入材料时，放电重复率和电荷消散速率与表面电阻率呈正相关。区域三与区域一、二对比，说明存在明显的电荷注入效应时，表面电阻率对放电重复率和电荷消散速率影响不明显。

对于未干燥处理的层压纸板，周期内存在指数分布现象，但各周期之间放电次数无衰减，说明其表面存在电荷积累但电荷消散的时间常数小于T2=10 s。

图6中各种材料第1周期放电次数的时间函数

N(t)=C1(1-C2exp(-t/τ)).

(8)

式中：C1、C2为常系数；τ为时间常数。绝缘介质可以视作电容与电阻并联的阻容模型，PE样本的电容为203.59 pF，电阻为10 TΩ，代入式 (8) 得到拟合值与实际值的比较如图7所示。

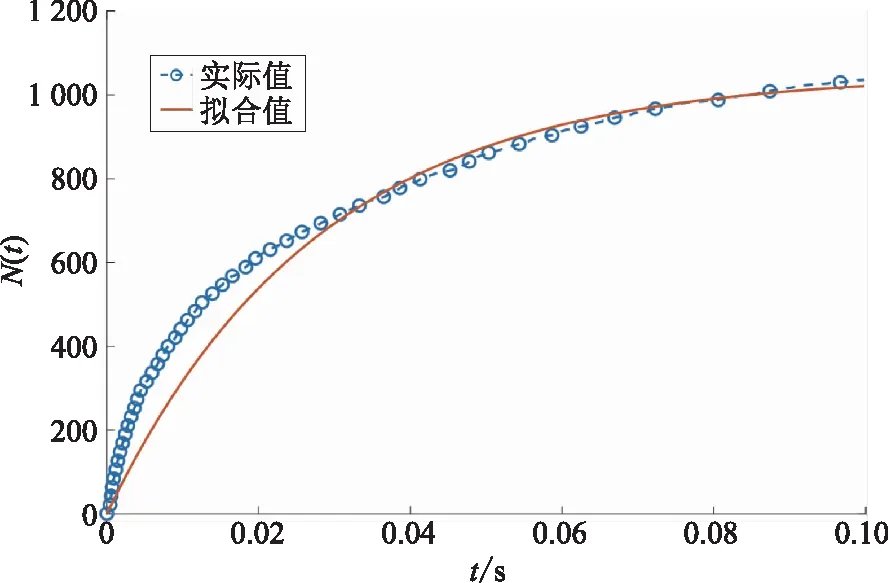
图7 PE样本放电次数实测值与拟合值

3.2 放电间隔的影响

显然，T2=10 s的恢复阶段远不足以使除层压纸板外的其他绝缘材料表面电荷完全消散，因而形成了随周期数逐渐递减的放电重复率。可以推测，如果恢复时间足够长，其他绝缘材料也会有类似于层压纸板的放电次数增长趋势。为了进一步验证，以PE为例，同样的试验平台，仅改变T2阶段时长(从10 s变为2 min)，进行同样8个周期的放电次数统计，结果如图8所示。

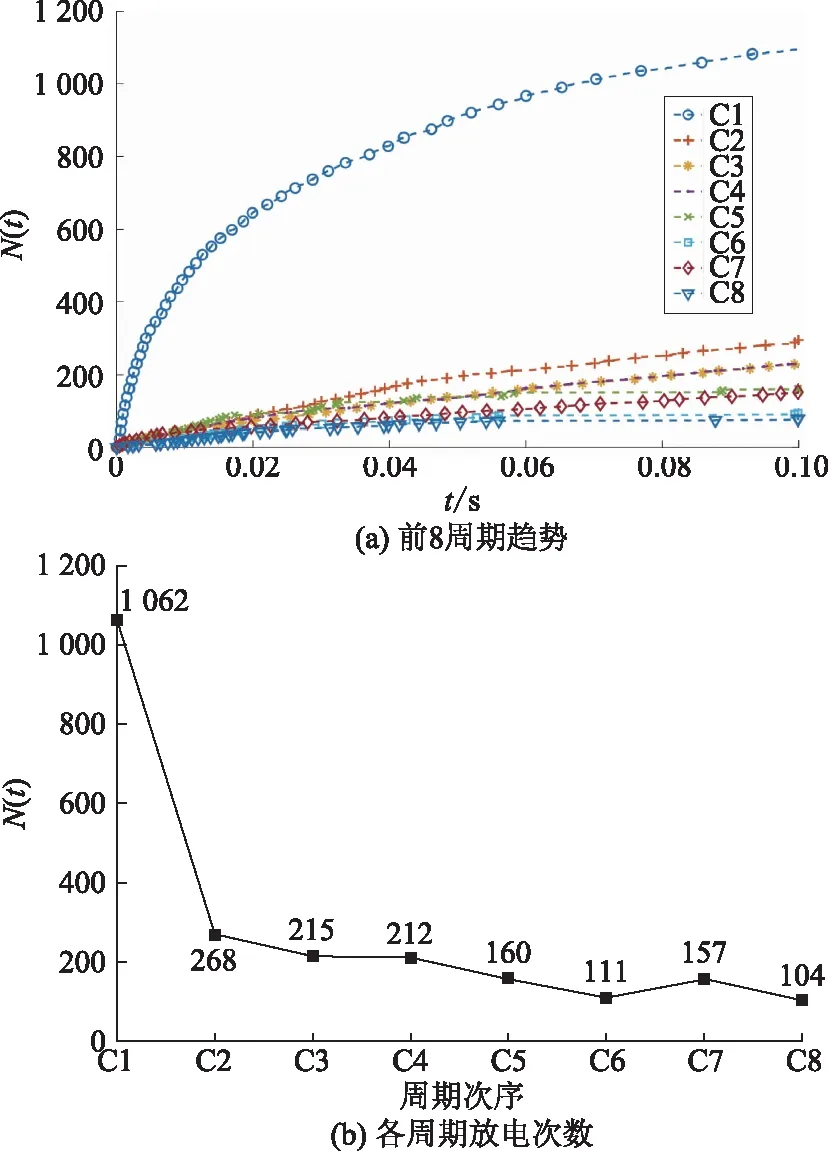
图8 6.4 kV下恢复时长2 mins，PE前8周期放电次数N(t)与时间t的关系以及各周期放电次数曲线

相比于T2=10 s的曲线，T2=2 min的曲线在第1周期无明显变化，而之后各周期的放电重复率有明显的提升，并且单周期放电次数饱和值更高。说明在恢复时间增长后，表面电荷的中和与消散程度更大，下一周期起始时的表面电荷密度减小，从而表面的反向电势减弱，对局部放电行为的阻碍也减弱，表现为更高的放电重复率。

基于这一规律，对于不同材料，通过调整脉冲间隔T2的时长，使得各周期放电次数相等、放电曲线重合，此时的T2可近似看作该材料表面电荷消散的时间常数。这一方法可以对不同绝缘材料表面电荷消散的时间常数估计，反映出不同绝缘材料的表面电荷积聚与消散特性。

进一步绘制单周期放电次数饱和值与脉冲间隔T2的关系曲线，结合材料表面电荷测量技术，得到相应的表面电荷水平，从而可以分析表面电荷、放电重复率以及脉冲间隔的相关性，有助于对表面电荷的积聚与消散过程以及其对放电的影响有更深的理解。

3.3 电缆的介质阻挡放电

实际工程应用中，不同的电气设备具有不同的绝缘几何结构。为了研究绝缘几何结构的影响，以电缆为例，本文使用Habia公司生产的基于高纯度FEP新型耐温绝缘电缆进行相似的试验。试验方法不变，不同之处在于：电缆材料表面是圆筒状绝缘结构；其次，电缆接地端为缆芯而非黄铜平板电极。这2个因素都会影响绝缘表面电荷的分布情况，进而影响放电重复率。

对样本平台进行改进，电缆绝缘层长100 mm，裸露的导体层长10 mm。用专用剥除工具将电缆表面半导体层剥除，使切面光滑，无毛刺，无半导体层残余，避免对放电重复率造成影响。将电缆置于针电极正下方，针尖端对准电缆中心点，针尖端与电缆中心点之间的空气间隙长度同样为10 mm，样本平台示意图如图9所示。

图9 电缆样本试验平台示意图

同样对电缆样本施加6.4 kV的负极性周期脉冲方波电压，测量其前8周期的局部放电次数，其中电缆PDIV为3.9 kV。前8周期电缆绝缘层阻挡放电情况如图10所示。

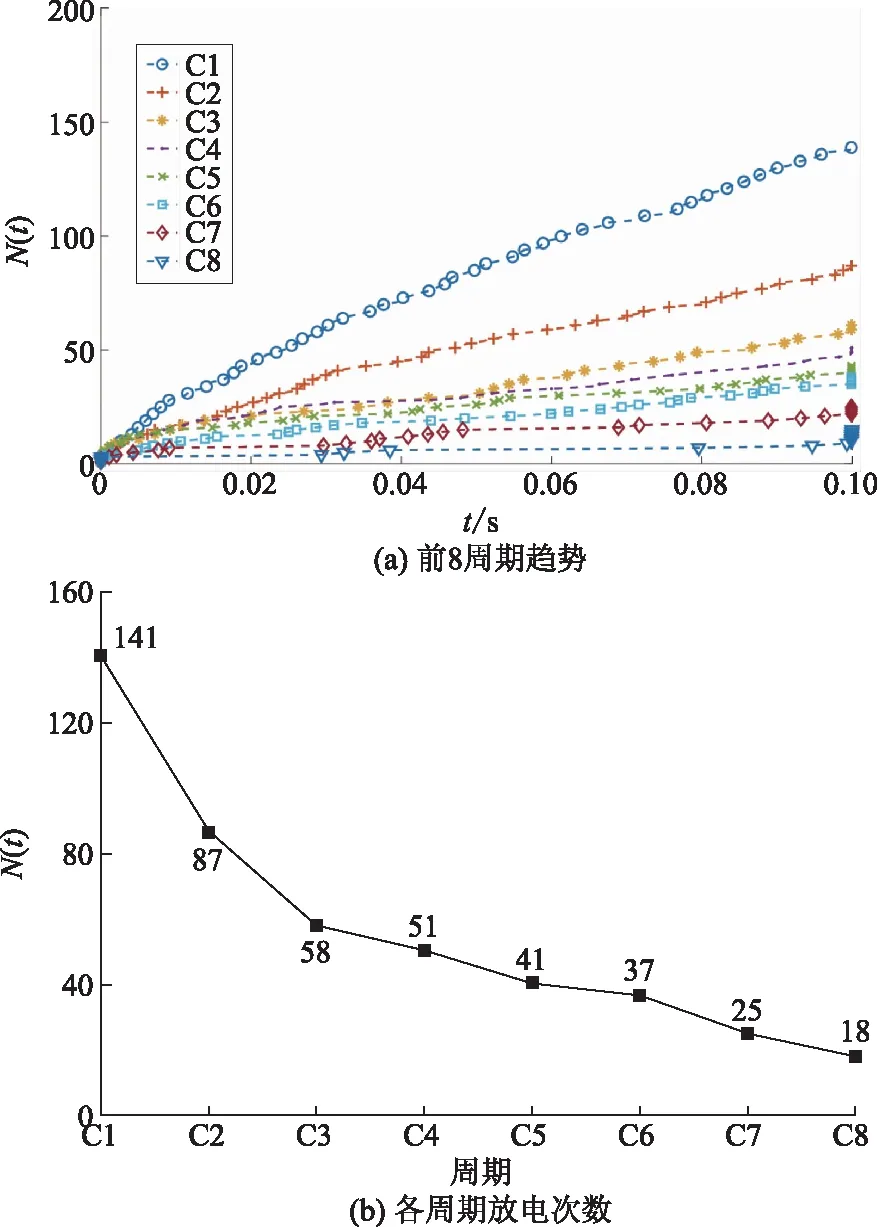
图10 电缆样本在6.4 kV下前8周期放电次数N(t)与时间t的关系以及各周期放电次数曲线

由图10可以看出，电缆样本各周期的负指数分布趋势和各周期局部放电次数衰减特性均较片状绝缘材料弱。周期内负指数分布趋势减弱的主要原因：是电缆表面呈线形筒状，电缆直径较小，所以除了电缆轴向的电荷积累产生的反向电势比较强，其他方向由于材料形状与表面积的限制，产生的反向电势均较弱，导致单个周期内放电重复率dN(t)/dt降低的趋势变小；其次由于接地极连接在裸露的缆芯上，与电缆表面的距离更近，使每一周期在电缆绝缘层表面积累的电荷更易沿接地极方向径向消散，从而各周期之间局部放电次数下降的趋势也较片状绝缘材料更弱，这一现象在电缆接头附近更加明显[26]。同时，该电缆样本的表面电荷消散时间常数也较本文中其他片状绝缘材料(除层压纸板外)更小。