基于蒙特卡洛模拟和综合评判法的配电变压器抗短路能力评估

陈友鹏，陈璟华，何东升，罗海凹，张兆轩，胡文波

(1.广东电网有限责任公司佛山三水供电局，广东 佛山 528100；2.广东工业大学 自动化学院，广东 广州 510006；3.国家中低压输配电设备质量监督检验中心，广东 东莞 523325)

配电变压器是配电网中至关重要的电力设备之一，是联接配电网和用户的重要枢纽。目前我国的配电变压器抗短路能力参差不齐，与发达国家的水平存在一定的差距。为了减少劣质配电变压器进入市场，电力检测机构必须在配电变压器的质量检测上提高水平。配电变压器抗短路能力的评估方法主要分为评估分析法和试验法。评估分析法主要有有限元分析法、专家评估法、运筹学方法、模糊数学法等，这些方法虽然能够在某一方面准确评估配电变压器的抗短路能力，但是缺乏全面性。试验法主要是指配电变压器的短路承受能力试验[1]，该方法能够直接判断配电变压器的抗短路能力，但是会对配电变压器造成一定的永久性损伤，缩短配电变压器的绝缘寿命。为了兼顾以上2种方法的优点，本文利用蒙特卡洛模拟和综合评判法对配电变压器的抗短路能力进行有效、准确的评估。

目前，配电变压器抗短路能力评估方法中应用较为广泛的是有限元分析法，该方法基于磁矢量有限元计算，动态模拟计算内部漏磁场和机械力。左秀江等利用模糊层次分析法(analytic hierarchy process，AHP)对变压器抗短路能力进行评估[2]，建立了基于有限元分析法的变压器抗短路能力模糊层次分析模型，根据有限元方法计算变压器高低压绕组的轴向和辐向受力情况。该方法虽然排除了指标定性过程中人为主观因素的干扰，但考虑的影响因素不全面，且无法避免专家打分过程的主观性[3-6]。为了克服上述缺点，本文充分考虑各种因素对电力变压器抗短路能力的影响，从电力变压器原材料使用[7]、制造工艺[8]、高低压绕组轴向和辐向受力情况[9]出发，采用模糊数学评价方法，将定性问题定量化，定性与定量相结合，克服以往评价系统中存在的模糊性和不确定性弊端，以便更好地反映实际情况。

本文根据各影响因素提出一个配电变压器的抗短路能力评价体系，建立一个更全面的综合评价模型。其次，针对传统单值打分模式主观性过强的缺点，利用蒙特卡洛模拟法模拟区间随机打分，结合AHP的主观权重和熵权法的客观权重得到综合权重。最后，利用评价模型对实际配电变压器进行抗短路能力评估，并与试验法进行比较，验证该模型的有效性和准确性。

1 基于模糊综合评判法的综合评价模型

1.1 配电变压器抗短路能力综合评价体系

为了对复杂问题进行有效分析，利用模糊AHP对复杂问题进行分层分析。AHP将一个复杂的多目标问题作为一个系统，将目标分解为若干准则，进而分解为准则的若干层次，通过定性指标模糊量化方法算出层次权重和总权重，构建多指标评估系统。该方法对主要影响因素进行归纳整理，按类型划分为相互联系的有序层次[10]。系统根据对客观事实的主观认识，将专家意见和分析者的客观判断有效结合。为了定性地描述影响因素的权重，采用标度法对各指标层中的影响因素进行重要性比较。在构建评价体系前，需确定影响评价对象的因素，由这些因素组成数学模型中的因素集，1个因素集表示1个评价指标。如含有n个影响因素，则评价指标为U={U1,U2,…,Un}。

由于影响配电变压器抗短路能力的因素复杂多样，需建立多层次的评价指标体系。根据GB/T 1094.5—2016《电力变压器 第5部分：承受短路的能力》，将电力变压器抗短路能力的影响因素分为4类——原材料、制造工艺、高低压绕组辐向受力及其安全系数、高低压绕组轴向受力及其安全系数，以此作为一级评价指标，并在每个一级指标下设若干二级指标，如图1所示。

图1 配电变压器抗短路能力评价指标体系

1.2 基于有限元的配电变压器短路受力仿真

计算变压器的短路受力，通过基于磁势矢量的有限元计算方法动态模拟变压器的内部漏磁场[11]和机械力。计算过程针对各绕组、铁心、夹件建立空间模型，参数包括绕组几何参数、匝数、垫块和撑条的尺寸和数量等。计算结果包含各相高低压绕组辐向压缩力、拉伸力[12]，轴向压缩力、拉伸力[13]等，对变压器内部各部分受力情况进行模拟。

为便于分析，将磁场按照线性分布进行考虑，向量磁位A则自动满足∇·A=0，待求解方程组为：

(1)

式中：J为导体电流密度向量；c为常数；μ为介质常数；A|S为场域边界s上的向量磁位值。

所对应的条件变分问题为：

(2)

式中：F(A)为导体受力函数；Q为泛函的空间取值范围。

内部场域的能量泛函即为F(A)。利用极值理论，可求得变分条件限制下的等价方程组。离散化后的有限元方程为

KA=P,

(3)

式中K、P为离散化后得到的单元系数矩阵。

根据内部场域的向量磁位A，即可求得磁感应强度矩阵

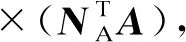
(4)

式中NA为分布函数矩阵。则导体受力

(5)

式中V为导体的体积。

根据上述计算方法计算配电变压器在高低压绕组的轴向受力和辐向受力，并结合材料的屈曲强度分别计算各绕组各方向的受力安全系数，以此作为配电变压器抗短路能力的二级指标，如图1所示。

1.3 确定评语等级

评语等级是划分评价象等级的标准[14]，通过评语等级能够确定评价对象的优次。一般评价体系中的评语等级表示为Y={Y1,Y2,…,Ym}，m为评价体系等级个数，由评价体系的实际情况确定。

为了更加准确地评价对电力变压器抗短路能力，将评价指标分成优、中、一般、差4个等级，见表1，其中：“优”和“中”2个等级代表配电变压器具有良好的抗短路能力，符合国家生产要求；“一般”则表示配电变压器的抗短路能力还有所欠缺，处于国家标准的临界范围；“差”则代表配电变压器达不到标准要求，无法投入实际应用。各指标等级评分标准见表2。

表1 各等级的评分区间

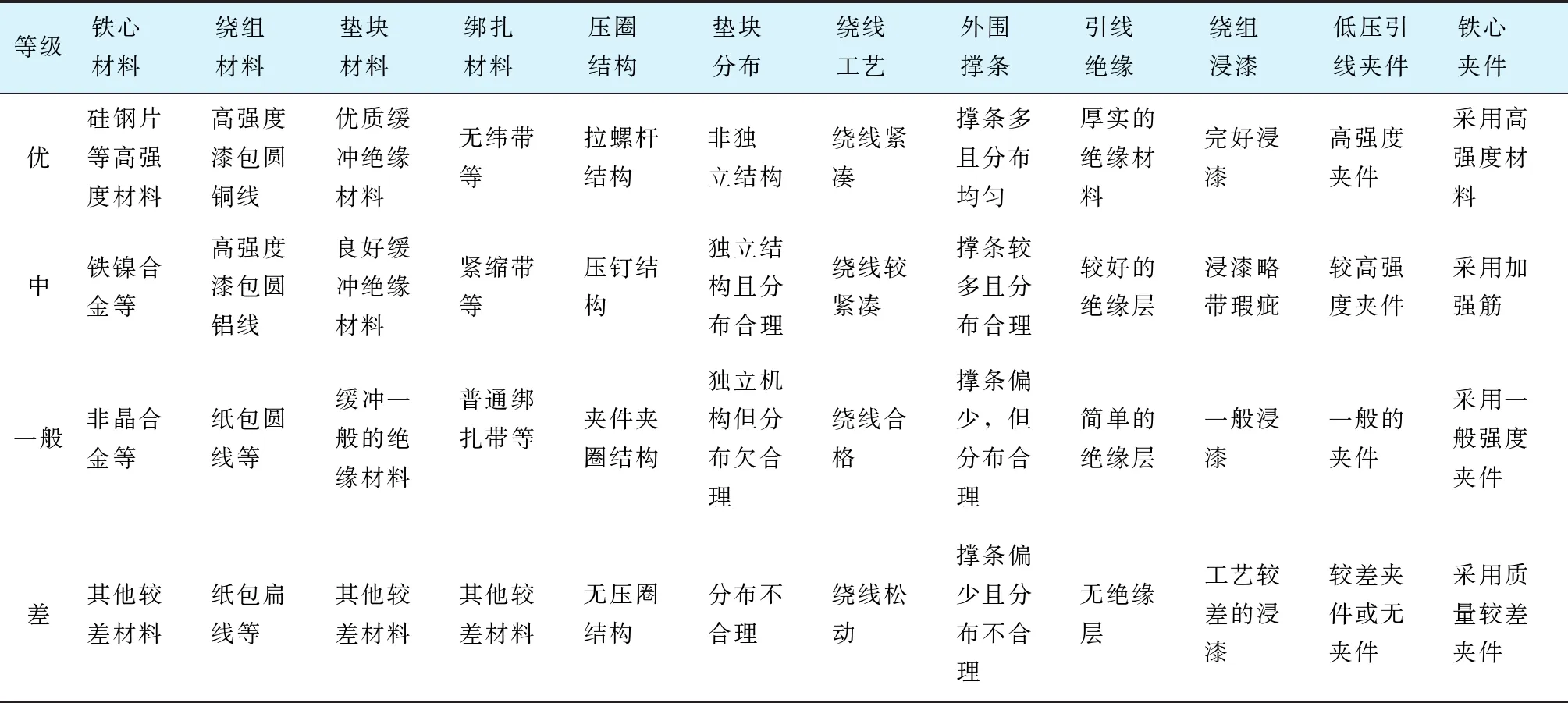
表2 各指标等级评分标准

1.4 隶属度函数及模糊评判矩阵

隶属度函数来源于模糊数学，用于表示任一元素i对模糊集合Y的隶属程度[15]，为元素和模糊集之间的相似程度提供度量。隶属度函数Ui的值介于0～1，越接近于1说明隶属程度越高，反之越靠近0则说明隶属程度越低。设置合理的隶属度至关重要，它不仅能反映模糊对象的本质，还能体现更多有价值的信息。根据评价对象的特点，本文采用岭型隶属度函数，如图2所示。

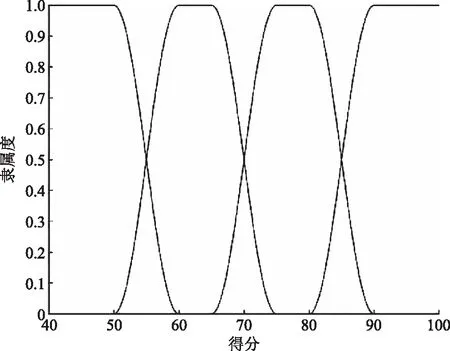
图2 岭型隶属度函数

每个岭型函数对应1个评价等级得分区间[16]，根据各指标因素的平均得分，计算各指标对应等级的隶属度，从而构造一个模糊评价矩阵R[17]。如二级指标含有20个影响因素和4个评价等级，则建立20×4的模糊评价矩阵。

1.5 评价因素的模糊权重向量

本文的模糊权重向量分为主观权重向量和客观权重向量，前者根据专家打分和软件仿真计算得出，后者根据熵权法计算得出，两者相结合得到更能反映客观事实的综合权重向量。

1.6 模糊综合评价结果

通过上述步骤确定评价体系的权重向量及模糊评价矩阵R，模糊综合评价模型可表示为：

D=ER，

(6)

G=DY.

(7)

式中：D为模糊评价结果向量；Y为模糊判断向量，本文取Y=(90,75,60,45)T；G为单次评价的最终结果。

为了使评估结果更具客观性，专家组对实例变压器的各项二级指标进行打分，根据专家组的打分形成各指标的打分区间，对各指标的打分进行蒙特卡洛模拟。为使模拟更具客观性，本文将迭代总次数设为N=100 000，最后统计所有评估结果出现在各等级的次数。整体的配电变压器抗短路能力评估流程如图3所示，其中k为迭代次数。

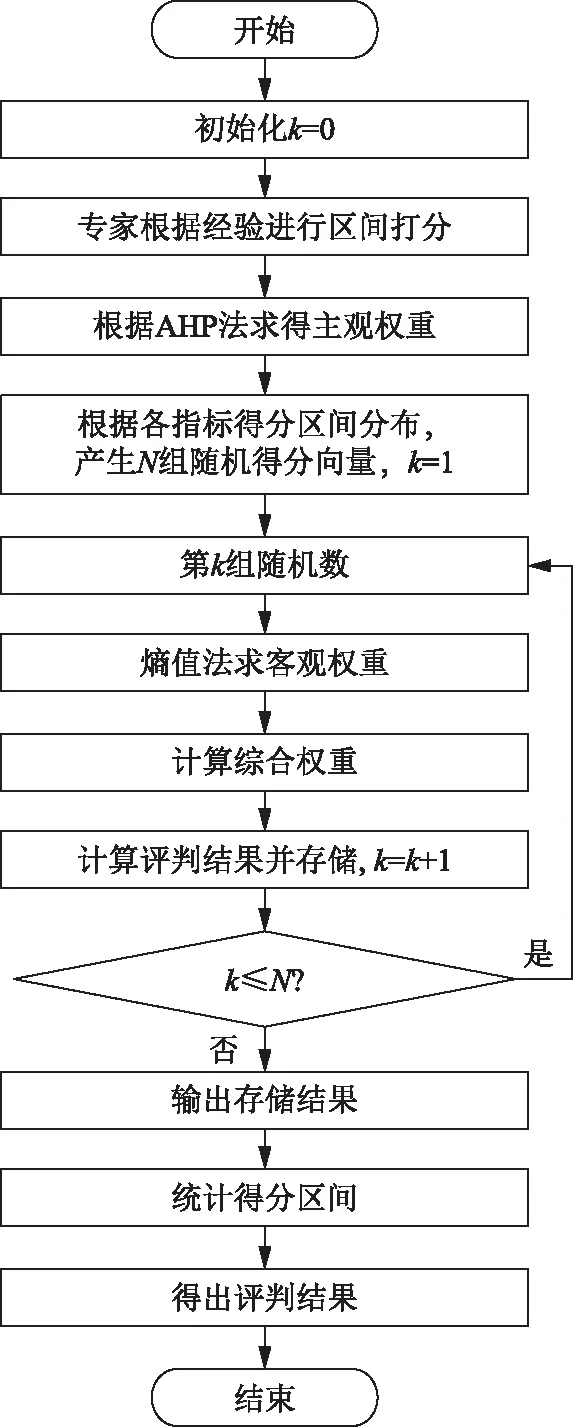
图3 配电变压器抗短路能力评估流程

2 综合权重的确定

2.1 主观权重

为确定各指标因素对于各级指标的重要程度，由专家根据其经验比较两两因素之间的重要性，构造各级指标的比较矩阵。根据比较矩阵计算其最大特征向量和最大特征根，并对最大特征向量进行归一化处理，由此得到该指标的权重向量。当评级体系具有多级指标时，采用1-9标度法[19]逐层对各级指标构造比较矩阵。标度法的具体含义见表3。

表3 1-9标度法含义

根据各级指标的判断矩阵，计算判断矩阵的特征向量ω和最大特征值λmax，将特征向量归一化，可得到对应的指标权重向量W=(w1,w2,…,wn)。

由于其他因素可能会对比较矩阵产生干扰，为保证可信度和准确性，对比较矩阵进行一致性检验，检验指标为：

(8)

(9)

式中：RC为一致性比率，当RC<0.1时，认为比较矩阵具有很好的一致性，否则需调整比较矩阵的取值，使之满足要求；IR为随机一致性指标，可根据矩阵阶数查表4得出，其中t为比较矩阵阶数。

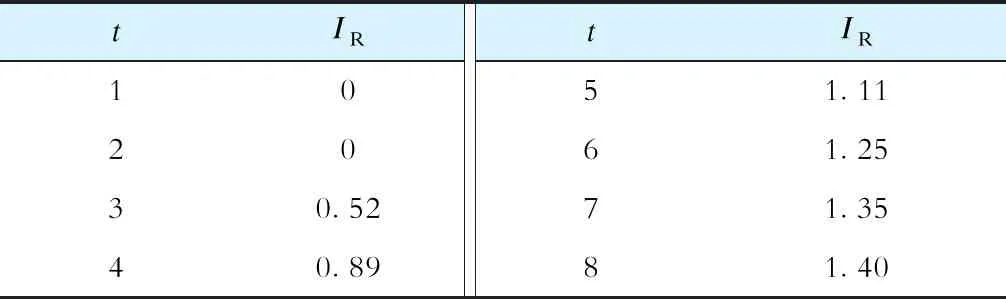
表4 随机一致性指标

2.1.1 一级指标主观权重的确定

为了避免单个专家的片面性，征求6位在变压器行业工作多年的资深专家意见，以2位专家为1组，根据表3的含义对图1的一级指标层的两两因素进行重要性比较，形成1个4×4×2的矩阵，其中第1组专家的一级指标评分见表5。

表5 第1组专家的一级指标评分

每位专家的知识和经验不一样，在各项评分中带有一定的主观性，所以对同一项目的评分可能存在差异。2个相同因素的重要程度相等，所以表5中的主对角线上的元素均为1。对于表5中的其他元素，如第1行第2列为原材料与制造工艺之间重要性比较，(1/2，1/2)为专家1和专家2的评分，1/2说明2位专家均认为原材料比制造工艺稍微不重要。根据表5形成1个比较矩阵T，再将矩阵T拆分为矩阵T-和矩阵T+：

分别求解2个拆分矩阵最大特征根对应的归一化特征向量：λ+=(0.088, 0.157, 0.483, 0.272)，λ-=(0.087, 0.143, 0.385, 0.385)。

2个子矩阵对应的权重向量分别为：

w-=αλ-,

(10)

w+=βλ+.

(11)

根据T+和T-求解α和β，求得α=0.998 7，β=0.999 2。

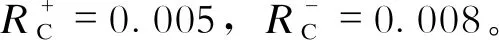
同理，根据其他2组专家比较矩阵，得到另外2个一级权重指标主观权重向量：WA2=(0.085, 0.117, 0.489, 0.309)，WA3=(0.075, 0.143, 0.518, 0.264)。

取三者平均值，得到最终的一级指标主观权重向量WA=(0.081, 0.137, 0.481, 0.301)。

2.1.2 二级指标主观权重的确定

同理，按照以上方法分别确定4个一级指标下的二级指标，以上3组专家给出了对应原材料的二级指标比较矩阵分别为：

这3个比较矩阵对应的主观权重向量分别为：WB11=(0.062, 0.194, 0.372, 0.372)，WB12=(0.079, 0.158, 0.468, 0.295)，WB13=(0.078, 0.132, 0.303, 0.487)。因此，原材料的二级指标主观权重向量WB1=(0.073, 0.161, 0.381, 0.384)。

这3个比较矩阵对应的制造工艺二级指标权重向量分别为：WB21=(0.038, 0.055, 0.042, 0.050, 0.049, 0.349, 0.315, 0.078)，WB22=(0.036, 0.089, 0.029, 0.100, 0.070, 0.329, 0.261, 0.078)，WB23=(0.028, 0.049, 0.028, 0.070, 0.076, 0.364, 0.296, 0.081)。因此，制造工艺的二级指标权重向量WB2=(0.034, 0.064, 0.033, 0.073, 0.065, 0.347, 0.291, 0.079)。

这3个比较矩阵对应的高低压绕组辐向安全系数二级指标主观权重向量分别为：WB31=(0.144,0.372,0.144,0.340)，WB32=(0.125, 0.387, 0.135, 0.353)，WB33=(0.133, 0.397, 0.137, 0.337)。因此，高低压绕组辐向安全系数的二级指标权重向量WB3=(0.134, 0.385, 0.138, 0.343)。

高低压绕组轴向安全系数的二级指标权重向量WB4与辐向安全系数一致，即WB4=(0.134, 0.385, 0.138, 0.343)。

2.2 客观权重

客观权重与配电变压器具体情况相关，反映配电变压器实际的抗短路能力。为了能够增加评估过程的客观性，引入蒙特卡洛模拟。蒙特卡洛模拟又称多概率模拟，是一种以概率统计理论为指导的数值计算方法，常用于模拟一个随机过程中不同结果可能出现的概率，但蕴含的随机变量的干扰使得模拟过程变得不易预测。专家根据配电变压器的具体情况给出各指标打分区间，在单次评估中利用蒙特卡洛模拟随机产生1组分数，再利用隶属度函数建立模糊评判矩阵求取客观权重。

系统同一层次中第i个指标的熵值

(12)

(13)

同理可求得其他指标对应的权重，由各权重组成该指标权重向量W′=(w′1,w′2,…,w′n)。

2.3 综合权重

为了兼顾决策者经验知识的主观性和变压器的实际情况，增加指标权重值的可靠性和真实性，本文采用线性加权法来求取综合权重。根据上述求得的AHP权重向量W、熵权法权重向量W′，得到综合权重向量E=(e1,e2,…,en)，其中

ei=ηwi+(1-η)w′i.

(14)

式中：η为线性加权系数；当η=1时，对应AHP；当η=0时，对应熵权法；本文中η取0.5。

3 实例分析

3.1 变压器实际情况

为验证上述评估方法的有效性，对3台不同容量的配电变压器进行校核，3台变压器的型号分别是S13-M-400/10、S13-M-200/10、SBH15-M-500/10，相关参数见表6和表7。

表6 配电变压器主要参数

表7 配电变压器绕组参数

以配电变压器S13-M-400/10为例，变压器材料采用的是高强度硅钢片、漆包圆铜线、层压木垫块、紧缩带绑扎材料，整体采用拉螺杆的压圈结构，采用独立垫块且分布较合理，引线的绝缘层结构良好，铁心采用加强筋结构，整体工艺良好。

采用ANSYS Maxwell对配电变压器进行受力仿真计算，图4为0.01 s时A相高低压绕组的短路受力情况，表8为配电变压器3种分接状态下的最大轴向力和辐向力的计算结果。

图4 400 kVA配电变压器A相高低压绕组的短路受力情况

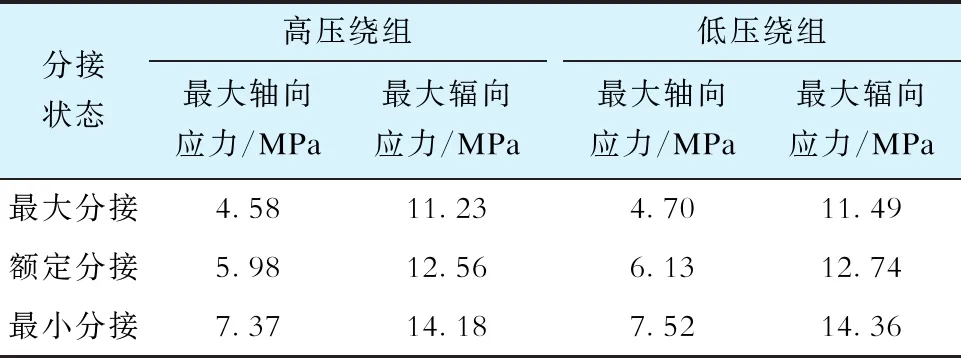
表8 400 kVA配电变压器3种分接状态下的高低压绕组最大表面应力

GB/T 7673.1—2008《纸包绕组线 第1部分：一般规定》附录A给出了半硬铜导体性能指标[20]。由于高低压绕组导线均为C1型，取规定非比例延伸强度Rp0.2为180 N/mm2，则导线的许用应力为0.2Rp0.2，即90 MPa。由表8可知：3个分接档下高低压绕组的受力均远小于90 MPa，在材料许用范围内；最小分接档下的绕组受力最大，其次为额定档；3个分接档下的辐向受力都比轴向受力大。

3.2 配电变压器的模糊综合评价

根据影响配电变压器抗短路能力评价的指标，结合仿真结果，邀请专家对S13-M-400/10配电变压器进行现场评估，并对图1所列的20个二级指标分别打分。综合3组专家的打分，得出所有二级指标的打分区间为：[91, 95]、[89, 95]、[90, 94]、[78, 81]、[89, 94]、[79, 84]、[79, 84]、[75, 80]、[78, 82]、[72, 76]、[74, 80]、[85, 90]、[88, 92]、[87, 90]、[87, 91]、[85, 88]、[92, 94]、[91, 95]、[93, 95]、[92, 95]。

根据上述打分区间利用蒙特卡洛模拟随机产生1组二级指标分数，如：93、92、92、79、91、81、81、77、80、74、77、87、90、88、89、86、93、93、94、93。结合式(12)和式(13)计算客观权重，得到客观权重向量为(0.052, 0.052, 0.052, 0.052, 0.052, 0.043, 0.043, 0.052, 0.050, 0.052, 0.052, 0.050, 0.052, 0.050, 0.052, 0.043, 0.052, 0.052, 0.052, 0.052)。

根据式(14)得出综合权重向量E=(0.029, 0.032, 0.039, 0.042, 0.028, 0.026, 0.024, 0.031, 0.029, 0.050, 0.046, 0.030, 0.058, 0.119, 0.059, 0.103, 0.046, 0.084, 0.047, 0.077)。

根据式(6)和式(7)计算得出综合评价结果为86.079。这次评分处于[85, 90)区间，说明该变压器的抗短路能力属于“优”等级。但由于单次评分具有偶然性，按照图3的流程进行蒙特卡洛模拟，迭代100 000次。

迭代模拟后评估结果如图5所示。由图5可知，该配电变压器有83.442%的评分位于[85, 90)区间，16.558%的评分位于[80, 85)区间。83.442%的评分属于“优”等级，16.558%的评分属于“中”等级，该变压器具有较好的抗短路能力。

图5 400 kVA配电变压器评估结果

对于S13-M-200/10，评估结果显示58.327%的评分位于[50, 55)区间，41.673%的评分位于[55, 60)区间。58.327%的评分属于“差”等级，41.673%的评分属于“一般”等级，该变压器抗短路能力较差。

对于SBH15-M-500/10，评估结果显示62.5%的评分位于[70, 75)区间，37.5%位于[75,80)区间。所有评分都属于“中”等级，该变压器的抗短路能力良好。

3.3 现场试验验证

对于电力变压器抗短路能力的评价，国内主要参考GB/T 1094.5—2016。该标准规定在外部短路故障的作用下，电力变压器不应出现损伤，影响正常工作[21]。由于试验配电变压器为具有2个独立绕组的三相变压器，根据上述标准只考虑三相短路，对称短路电流均方根值

(15)

(16)

式中：I为对称短路电流的均方根值；Zs为系统短路阻抗；Zt为折算后变压器的短路阻抗；Us为标称系统电压；S为系统短路视在容量。

为了对应评估模型的评估等级，根据GB/T 1094.5—2016将相电抗变化幅度划分为4个区间，见表9。除了相电抗值，还需要对变压器短路试验后的吊心情况进行分析。

表9 对应等级的相电抗变化幅度

表10给出了3台变压器各相的相电抗值。图6至图8为3台变压器短路试验后的吊心图片。

图6 400 kVA配电变压器短路试验后高压侧吊心

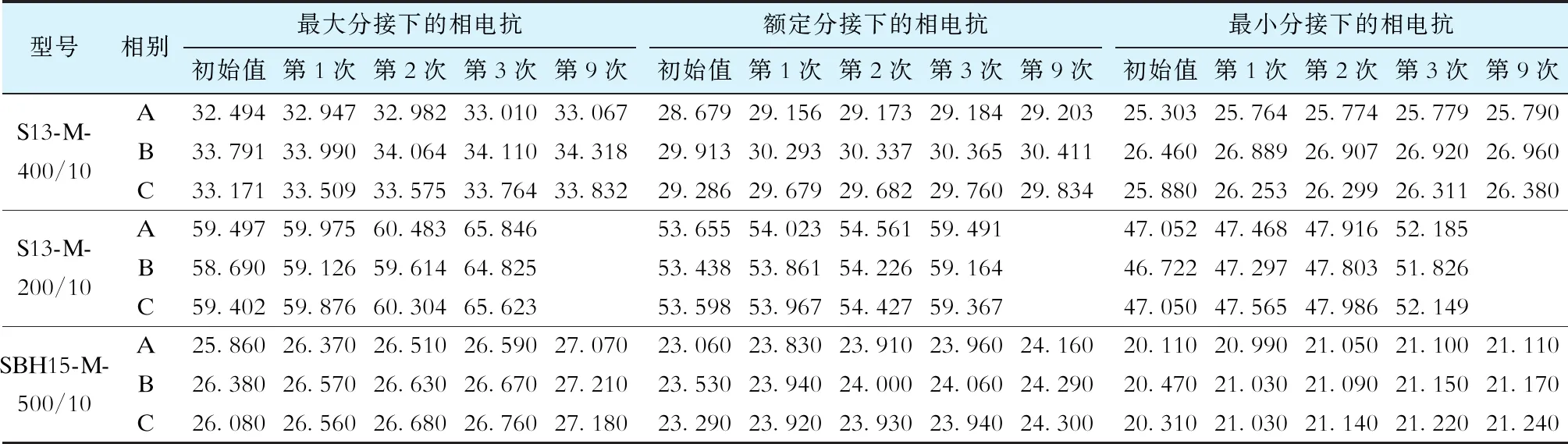
表10 3台变压器的相电抗值

图7 200 kVA配电变压器短路试验后高压侧吊心

图8 500 kVA配电变压器短路试验后高压侧吊心

S13-M-400/10配电变压器经过9次短路试验后的电抗变化均小于2%。试验后变压器吊心整体无变化，垫块无松动，无放电现象且短路后绝缘合格。

对于S13-M-200/10，前2次试验的相电抗变化小于2%，但第3次短路试验时相电抗突变，相电抗变化超过10%，鉴于试验的安全性，不宜继续进行短路试验。该变压器经3次短路试验后，试验电流异常，各相电抗变化均超过合格范围，吊心检查发现垫块移位明显，铁心铁轭错位，且短路试验后复试例行试验不合格。该变压器的抗短路能力评估等级与试验情况基本一致，该配电变压器抗短路能力表现差，无法达到生产要求。

SBH15-M-500/10配电变压器9次短路试验的最大相电抗变化为4.97%，整体结构良好，低压出线位置绝缘良好，垫块位置基本不变，表明其抗短路能力良好，与评估结果一致，能够满足正常的工作要求。

综上，3台变压器基于蒙特卡洛模拟和综合评判法的评估结果与短路试验结果基本一致，证明了本文所提方法能够在保护变压器的前提下，准确评估变压器的抗短路能力，为实际电力变压器的生产提供指导意见，减少劣质变压器流入市场。

4 结束语

现有的配电变压器抗短路能力评估方法缺乏客观性，部分评估方法效果不佳，同时短路承受能力试验具有较大破坏性。为了进一步提高配电变压器抗短路能力评估精度，提升评估的有效性，本文提出蒙特卡洛模拟和综合评判法相结合的方法，在有限元分析法的基础上，建立更为客观的配电变压器抗短路能力评估模型，从材料、制造工艺和短路受力3个方面对配电变压器的抗短路能力进行评估。

本文提出的配电变压器抗短路能力评估方法能够在不损坏变压器的前提下筛选出抗短路能力一般和较差的配电变压器，避免劣质产品进入市场，提高我国配电网的供电可靠性。