基于GERT网络模型的武器装备试验质量控制研究
2022-02-22白旭
白旭
(92941部队41分队,辽宁葫芦岛 125001)
1 引言
武器装备试验要求在规定使用环境条件下,对各项性能进行精准评价,同时得到是否符合指标要求的结论[1]。但因为武器装备结构与使用环境的复杂性,试验评估结果可靠性较差,直接影响武器的战术应用与作战效能,严格操控武器装备试验过程,是解决试验结果准确度不高的重要方式。
随机网络,又称图示评审技术(Graphical Evalualion Review Technique,GERT),表示网络计划内活动与活动间的逻辑关联不确定性,且活动费用与时间参数也是未知的,从而按照随机变量实施分析的网络计划技术。在GERT 网络内可涵盖拥有不同逻辑特性的节点,节点引出端容许具备多个概率分支,网络内可存在回路与自环,各个活动的费用及时间参数均能选择任何类别的概率分布[2-3]。GERT网络能够真实地展现出武器装备试验的全部进程,所以探究基于GERT 网络模型的武器装备试验质量控制拥有理论与应用上的双重优势。
本文构建一种基于GERT网络模型的武器装备试验质量控制方法。通过对试样数据的先验信息进行明确,运用贝叶斯方法计算试样的试样数量,确定试样容量,了解试样数量对测试结果的直接影响;划分试样阶段工作内容,采用工作分解结构法得到GERT试样网络模型,简化GERT试样的转换,求解试样的风险;采用计划、执行、检查与行动等动态循环策略,建立试样的质量控制模型,运用混合粒子群算法对模型求解,完成高效精准的试验质量控制目标,让试验结果最大程度接近实际操作结果,展现出武器装备的真实性能状态。
2 武器装备试验容量计算
采用贝叶斯(Bayes)方法分析武器装备试验过程,得到武器装备产品试验容量,探究增加试验次数对试验评定影响,提升试验质量控制经济性[4]。
Bayes估计是把未知分布参变量作为随机变量,同时具备先验分布π(θ),在得到试验样本后,使用Bayes公式算出未知分布参变量的验后密度:
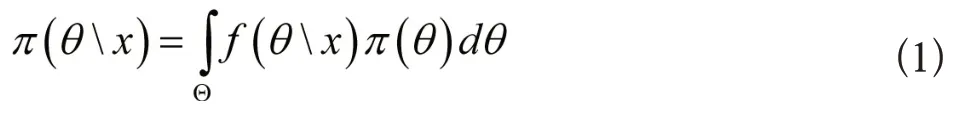
在统计推理中,将π(θx)当作Bayes检验的出发点,这时未知参变量θ的Bayes估计是:
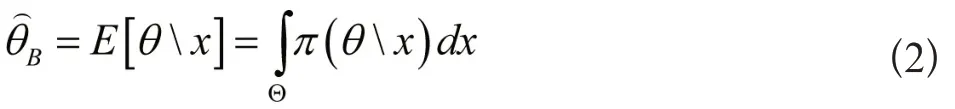
若置信度是1-α,则:

符合式(3)的(θ1(x),θ2(x))即为θ的区间估计。
假设先验分布函数是H(θ),先验密度分布函数是h(θ),将样本分布函数记作:
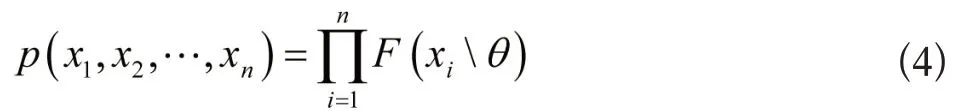

通常在试验设计中,若产品已经达到某个要求,就可以推算出参试产品个数,完成对试验样本容量的确定。
武器装备试验质量控制评估是判定其战术技术性能与作战效能的关键环节,武器装备越来越复杂,造价成本逐步上升,试验鉴定难度系数随之增加,试验周期与费用矛盾日益凸显[5]。使用Bayes方法解决统计问题过程中,在使用全部样本数据时,首先要得到先验信息,不同产品与不同特性的试验,其先验信息分布各不相等,按照实际试验特征,认定先验分布服从二项分布,也就是参数是p的二项分布,p代表合格率。
若X1,X2,…,Xn为参数p的二项分布样本,并保证在[0,1]上式均匀分布,那么p的先验分布密度是:

将样本分布列描述成:
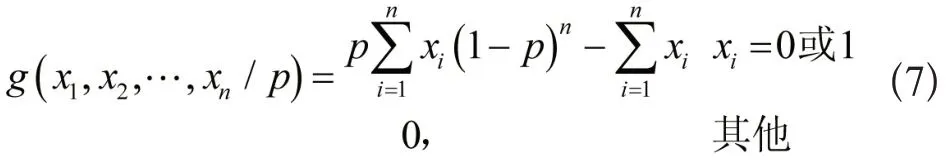
处在二次损失状态下,p的估计值是:
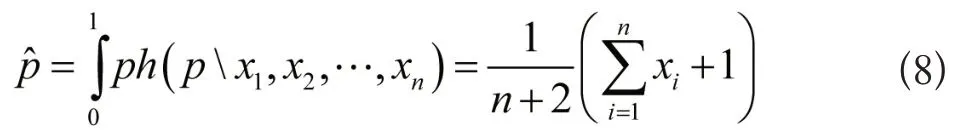
把试验容量记作:

在设计试验的过程中,可以事先预设试验样本总体符合设计需求,也就是产品设计指标已实现设定的水平标准,然后假设在全部试验内该指标合格次数是xi,代入求解。例如,在投弹试验中,设计需求命中靶心率是80%,预期在试验内命中靶心次数xi是4次,就可计算出试验容量是5次。
3 武器装备试验风险评估
在降低试验项目操作成本的同时,为了分析武器装备试验风险问题,按照工作分解结构法(Work Breakdown Structure,WBS),把武器装备试验过程划分成立项论证、方案论证、样机试验与武器定型四个阶段[6]。在GERT随机网络内,节点表示网络系统状态,箭杆表示状态间的转移,因此武器装备试验的GERT网络共拥有4个节点。
在广义随机网络内可设定三种输入类型与两种输出类型逻辑,组成六种不同逻辑性能的节点。在三种输入节点类型内,仅有“异或”节点拥有较为完整的数学描述,要把其中的“或”型及“与”型节点利用相应的网络逻辑转变为“异或”节点,组成仅有“异或”节点的网络[7]。GERT网络就是一种只包含“异或”节点的随机网络,获得图1所示的武器装备试验的GERT网络模型。
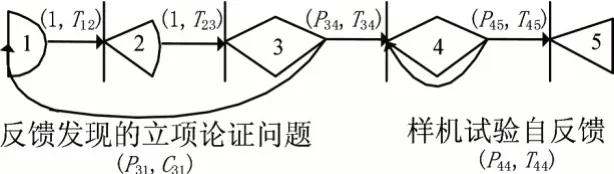
图1 GERT网络模型架构图
由图1所示,图内仅包含“异或”节点,在节点1 与节点3之间拥有一个环路,在节点4中包含一个自环。已知在仅包含“异或”节点的GERT网络内才具备准确的风险评估解,关于图1的GERT 网络,设定其进度风险随机变量为t,随机实数是s,则随机变量t的矩母函数是:


在图1内的GERT 网络模型内,一阶环共有2 个,依次是1→2→3→1与节点4内的自环,假设T(L1)是一阶环的传递系数,可得到如下公式:
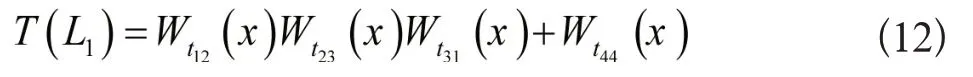
由此,获取从节点1至节点5之间的传递函数是:
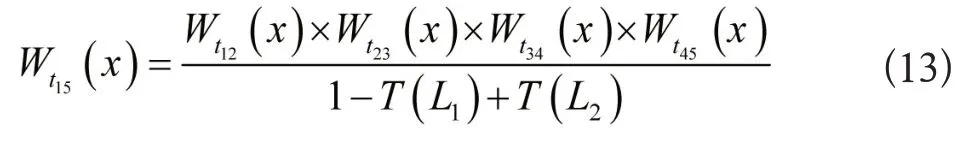
将节点1至节点5的等价概率解析式描述为:

进度风险均值公式为:

进度风险方差均值是:
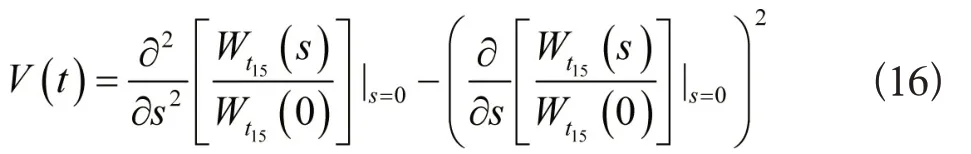
以此就能利用GERT 网络模型求解从源节点1 至终节点5间的进度风险传递问题,表明进度风险是通过均值E[t]、方差V[t]及概率P15在节点1与节点5之间实施传递。武器装备试验多数为系列开发,所以多数试验环节的风险分布规律可运用历史经验及相同项目进行分析,针对引进新技术、新工艺的试验环境,可采用专家经验得到风险分布函数[8]。
为了在GERT网络模型内获取准确的武器装备试验风险评估数值,就要对环路采取特殊处理,也就是利用等价转换,将包含环路的GERT网络逐渐简化,融合成一个确定型网络后,再实施模拟运算。在“异或”型的自环架构内,因为允许回路的次数是无穷次,得到:

式中,Pij表示转换后的传递概率,Pa是直线内的传递概率,Pb是自环内的传递概率。利用简化就能将随机网络更改成确定型网络,即完成风险评估的全部过程,从总体了解武器装备试验面临的时间和费用风险,为武器装备的成功应用奠定基础。
4 武器装备试验质量控制实现
4.1 基于PDCA的武器装备试验质量控制模型
在武器装备试验操作周期之内,怎样组织、计划并全方位进行试验质量控制是一个较为繁杂的系统工程问题。武器装备试验的质量控制模型表示一个指定的武器试验项目,在计划与控制质量方面,为科研团队提供一个详细的组织与实施指导框架。在质量控制体系内,PDCA,即计划(Plan)、执行(Do)、检查(Check)与行动(Action)是质量控制的动态循环,它能够在组织的各个过程中展开,和武器装备的策划、实施、控制与精进均具有密切关联。
在PDCA基础上,创建武器装备试验质量控制模型,如图2所示。
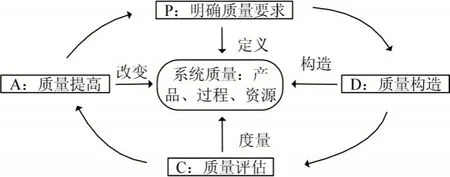
图2 武器装备试验质量控制模型架构
4.2 模型求解
对模型的求解就是对质量控制点的单目标多约束优化问题,粒子群算法在动态目标寻优方面具备收敛速率快,求解质量高,计算简便、鲁棒性优良等优势,具体计算公式为:
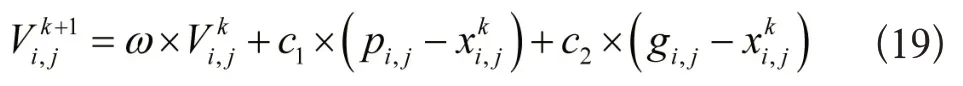
式中,c1、c2表示加速系数,通常情况下c1=c2=2,i={1,2,…,m},j={1,2,…,n},ω是惯性权重。
标准粒子群算法利用追寻个体极值与群体极值实现极值寻优过程,但伴随迭代数量的不断上升,在种群收敛集内的粒子也越来越相近,无法跳出局部最优解周边范围,产生早熟现象,而遗传算法对于全局搜寻性能更强,所以本文把两种算法进行融合,从而得到准确的武器装备试验质量控制模式。把粒子同个体最佳解Pbest与群体最佳解Gbest的交叉和粒子本身变异引入新种群,提高种群相关度,并把种群数值约束在指定范围中,降低计算量。
使用启发式算法解决质量控制问题,首先要采取编码设计,获得的优化结果就是工序Si内质量控制点Gij试验控制域Gij[r]的选择,yij代表工序Si的第j个质量控制点Gij相对的值,遗传算法染色体数量和粒子群相互对应,因此将编码方式记作:

基于PDCA的武器装备试验质量控制模型是在收敛条件下完成试验损失成本最小化,试验损失成本总数C就是模型的适应度函数值,将适应度函数描述为:
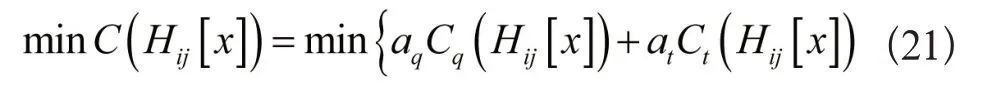
设定初始化控制参变量是w、c1、c2,随机生成n×m个粒子yij,同时推算其适应值,初始化速率是Vi,现阶段个体最优方位是Pi,群体最优方位是Pg。
改进粒子群算法的关键是借鉴遗传算法内的交叉过程,个体经过与个体最佳解Pbest与群体最佳解Gbest进行交叉更新,根据式(22)推算出自适应交叉率,使用交叉方法挑选两点交叉模式,减少因种群择取效果不佳导致优秀个体丢失现象,同时保障群体多样性特征,不会陷入极小值,提升方法计算效率,令其符合各收敛条件够,就会成为全新的种群个体。
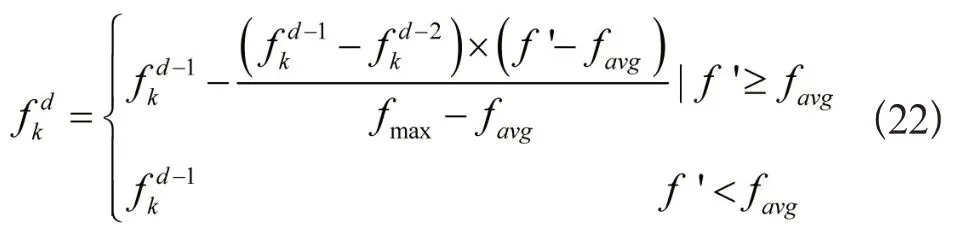
为了防止多种群混合粒子群算法因为参变量设定和时间影响,发生早熟现象,在计算时要对个体最佳方位Pbest采取一定概率变异操作,变异是小概率变异,不会发生优秀个体丢失。通过式(23)推算的概率即为种群Pbest变异概率。
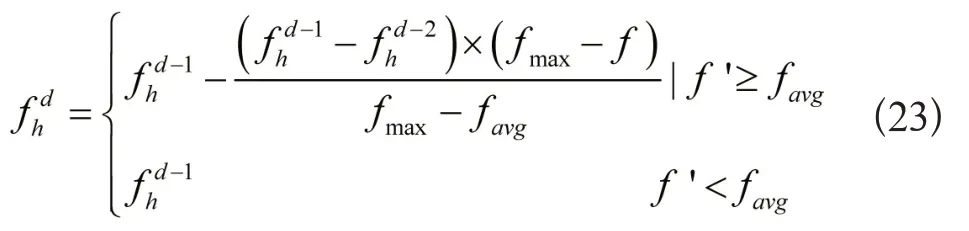
以上就是武器装备试验质量控制模型计算的全部过程,最终求解得到的数值就是试验质量控制的最优参数,实现高精度试验质量控制目标,为武器装备性能评价提供实质性帮助。
5 仿真实验
为了验证基于GERT网络模型的武器装备试验质量控制的效果及可行性,使用上述公式(23)对武器装备试验质量控制进行综合评判,以导弹武器装备试验为例,过程与数据结果如下。
首先是产品试验质量控制评估,输入初始数据,包含产品名称、部件名称等。其次输入评估指标检测值,计算型指标要输入公式内的计算值,评估型指标要输入初始评估结果。待全部单项指标检测数据全部录入完毕后,得到每个单项指标的真实评测值,如表1所示。
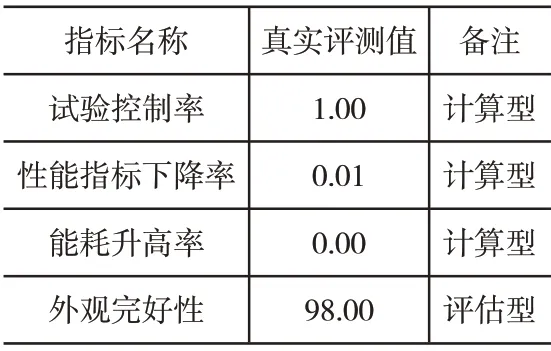
表1 部分单项指标真实评测值
通过将随机网络简化为确定型网络,即完整的风险评估过程,可以全面了解武器装备试验所需时间和费用的风险,为成功应用武器装备奠定基础。此产品试验质量综合评估结果如表2所示,总分数为100分。
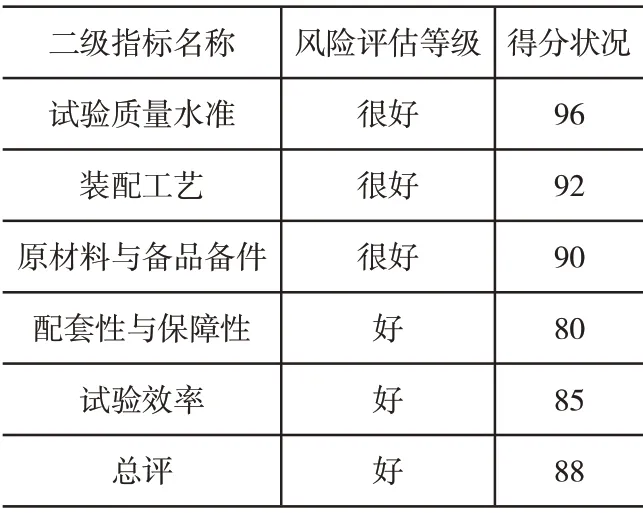
表2 产品试验质量控制综合风险评估结果
图3是试验质量控制的完工时间概率密度拟合曲线。
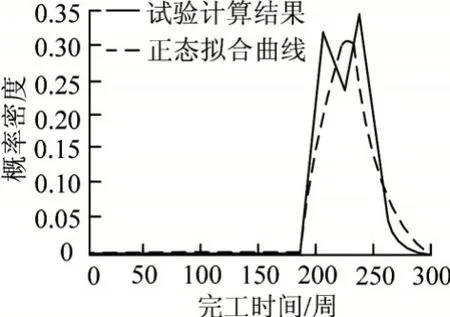
图3 产品试验质量控制完工时间概率密度拟合曲线
由图3可知,拟合优度表示回归曲线对观测值的拟合水平,拟合优度越接近1,证明拟合水平越好。图3内的拟合曲线优度超过95%,且在试验质量控制过程中,产品试验完工进度的概率密度分布服从正态分布。由此证明本文方法拟合精准度较高,具备优秀的鲁棒性。
6 结束语
由于武器装备结构和使用环境的复杂性,试验评估结果的可靠性较差,直接影响到武器的战术应用和作战效能,严格操作试验程序是解决试验结果准确性低的重要途径。为了更加真实呈现出武器装备真实性能,提出一种基于GERT 网络模型的武器装备试验质量控制方法。所提方法可有效对试验过程各因素进行精准控制,所得结果与真实结果相似度较高,对武器装备的实际应用具有参考价值。但在质量控制中,没有考虑控制权重大小问题,可能产生控制效率低现象,在下一步研究中会对该问题进行详细探究。
