物流配送车辆精细化多目标调度方法*

□ 曾 强，林 凯，王科峰

(1.河南理工大学 工商管理学院，河南 焦作 454000；2.河南理工大学 能源科学与工程学院，河南 焦作 454000)

1 引言

车辆调度是物流配送的关键问题之一。车辆调度直接影响着物流配送的成本、客户满意度、社会效益和经济效益。车辆调度问题(Vehicle Scheduling Problem，VSP)最早由学者Dantzig和Ramser于1959年提出[1]，已被证实为NP-Hard难题[2-3]，近年来一直是学术界的一个研究热点。

现有关于VSP的研究所涉及的优化目标主要有配送里程最少[4]、耗油量最低[5]、总运输时间最少[6-7]、客户满意度最大[8]等。这些研究在量化优化目标方面不够精细化，如成本目标、客户满意度目标等。对于成本目标，文献[6-7]仅把运输成本区分为固定成本和行驶成本。笔者认为，更为精细的方法是把运输成本细分为调车费、人工成本、车辆折旧成本、轮胎消耗费、耗油费、高速过路费等，而这些成本或费用直接与装车方案、配送路径、配送顺序有关。除此之外，现有研究在计算运输成本时未区分普通路段和高速路段[9]，这也与实际不符。实际上，高速过路费是根据车辆自重、当前车辆载重量和行驶里程进行计算的，这将直接影响到运输成本的准确性。对于客户满意度目标，它主要是由物料送达时间决定的，而物料送达时间取决于车辆出发时间、行驶时间和上一个客户的服务时间等，研究时应详细考虑其逻辑关系，从而更为有效地确定物料的送达时间，最终确定客户满意度。

在工程实践中，考虑到各种现实约束，VSP变得更为复杂。现有关于VSP的研究多集中于单目标、单车型优化问题，而对于多目标、多车型问题的研究很少。对多目标VSP算法主要有粒子群算法[10]、禁忌搜索算法[11]、NSGA II算法(Non-dominated Sorting Genetic Algorithm with elite strategy,NSGA II)[12]等。其中，NSGA II算法是Deb等[13]在NSGA算法的基础上提出的带精英策略的非支配排序遗传算法，是一种比较成熟和理想的Pareto寻优算法[14]。

基于以上分析，本文提出了一种物流配送车辆精细化多目标调度方法：建立了物流配送车辆精细化多目标调度模型，设计了带精英策略的非支配排序遗传算法(NSGA II)用于求解该模型。

2 模型构建

假设配送中心用p个车型的v车辆向n个客户配送一种货物，通过合理调度，使得配送任务的综合成本最低、平均客户满意度最大。

2.1 综合成本

综合成本根据式(1)进行计算。

综合成本=调车费+耗油费+人工费+过路费+车辆折旧费+轮胎折旧费+其他成本

(1)

2.2 平均客户满意度

(2)

(3)

3 NSGA II算法设计

以C#.NET为开发平台，设计了NSGA II算法求解模型。根据算法需要，定义了图1所示的自定义类型。其中，Chr表示种群数组，Chr(i)表示种群中的个体。

图1 自定义类型

3.1 编码方式

对于VSP，最直观的编码方式有基于车辆行驶路径的自然数编码[15]和基于客户的编码[16]，但这两种编码方式解决的VSP均是车辆数和车型没有限制的问题，无法用于求解本文模型。因此，本文在基于客户号的整数编码方式的基础上加以改进，采用固定长度为lens(lens=2×rp-1)的整数编码方式。式(4)中属性CO即为个体chr(i)的编码，根据每一条路径对应的总载重量约束来选择所需车型。这种编码方式可以很好地解决有车型限制、车数限制且实际所需车辆未知的VSP，并且在进行解码操作时可以直观地得到每辆车服务客户的情况。

chr(i).CO=(0 3 4 1 0 0 1 0 5 1 1 0 0 9 2 0 0 8 6 0 0 7 0)

(4)

3.2 种群初始化

采用如下步骤对种群进行初始化操作：根据编码ch.CO计算ch.nc、ch.f、ch.VS、ch.VM、ch.CC。若某车辆未找到合适的车型，则令ch.f=0且不再连续判断后续车辆的可行性，返回ch；反之，若所有车辆都找到了合适的车型，则ch.f保持为1，表示该个体可行，返回ch。

3.3 解码操作

解码操作的任务是对个体chr(i)，分别针对chr(i).O、chr(i).tm、chr(i).toc、chr(i).vd、chr(i).tc、chr(i).rt等参数进行计算。具体解码流程如图2所示。

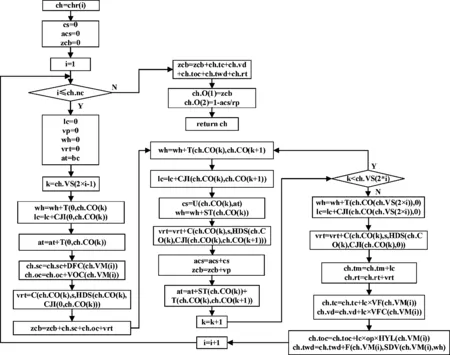
图2 解码操作流程

函数说明：

UCch.CO(k),at)作用是车辆在at时刻到达客户ch.CO(k)的满意度，由式(2)计算；F(ch.VM(i)、SDV(ch.VM(i),wh)作用是司机驾驶ch.VM(i)型车时，该车型司机工资标准为SDV(ch.VM(i))、工作时间为wh的工资；C(ch.CO(k),S,HDS(ch.CO(k),CJI(ch.CO(k),ch.CO(k+1)))作用是车辆服务客户ch.CO(k)后，该车辆载重量为S、高速收费标准为HDS(ch.CO(k))和行驶距离为CJI(ch.CO(k),ch.CO(k+1))的过路费。

3.4 遗传操作

遗传操作包括交叉操作和变异操作。采用“基于客户点顺序”的交叉和变异方式来进行交叉和变异。

①交叉操作。

根据个体编码方式的特点，交叉操作采用“两点交叉”方式。具体方法如下：设两个父代个体为a，b，首先，产生两个不相等的1～lens的随机整数c1,c2，若c2

②变异操作。

根据个体编码的特点，变异操作采用“两点交换变异”方式，具体如下：将父代个体P产生的两个不相等的1～lens的随机整数m1,m2作为变异点，对父代个体属性CO基因座m1和m2的值进行交换变异。

4 案例分析

为验证本文所提算法的有效性，将该算法在某物流企业的车辆调度中进行了应用测试。该物流企业共有13个客户，现需从配送中心调货，通过对配送车辆的合理调度，使得完成配送任务的总成本最小、平均客户满意度最大。

经算法独立运行20次，均能得到基本相同且均匀的Pareto解集，表明收敛效果较好。图3是某次进化计算得到的Pareto解集，其中，个体4的综合成本为17424元、平均客户满意度为0.5、里程为3198.75公里、调车费为3630元、过路费为4012.5元、油费为2487.19元、车辆折旧费为1754.52元、轮胎折旧费为520.16元；总需车数为6辆，车型分别为C、A、B、D、A、B；每辆车载重分别为16吨、4吨、11吨、17吨、9吨、11吨；C车型服务客户号为2、8、1的客户，A车型服务客户号为7的客户，B车型服务客户号为13、6的客户，D车型服务客户号为12、5、4的客户，A车型服务客户号为10、3、9的客户，B车型服务客户号为11的客户。

图3 Pareto解集

5 结束语

针对多车型、单配送中心车辆调度问题，提出了一种物流配送车辆精细化多目标调度方法：建立了以综合成本最低和平均客户满意度最大为优化目标的物流配送车辆调度模型，设计了带精英策略的非支配排序遗传算法(NSGA II)。在算法中，采用以客户号为基因值的固定长度整数编码方式进行编码，该编码方式更好地解决了有车型限制、车数限制且实际所需车辆未知的VSP；在解码中，对车辆调度过程中的成本、路径和时间进行精细化处理，实现了总利润和平均客户满意度的准确计算。