新型相干结构光场产生研究进展（特邀）

朱新蕾，余佳益，蔡阳健，

（1 苏州大学物理科学与技术学院，江苏苏州215006）

（2 山东师范大学物理与电子科学学院，济南250358）

0 引言

自1960年第一台激光器问世以来，激光作为一种全新的光源，由于其“三好一高”特性在国防、医疗、通信等诸多领域得到广泛的应用，对社会发展进步起到了重要的推动作用。随着对激光应用领域研究的不断深入，发现具有高相干性的激光会带来一些负面影响。比如，高相干性激光容易产生散斑现象、容易受到光阑衍射、波前畸变、大气湍流扰动等影响。而适当降低激光相干性，不仅可以保持激光原有的特性，还可以降低由于高相干性带来的诸多负面影响。因此，相干性逐渐成为除振幅、偏振和相位以外备受关注的光场第四个调控自由度。

光场的相干性包括时间相干性和空间相干性，前者与光束的单色性密切相关，后者与光束的方向性密切相关。本文仅对空间相干性进行讨论，本文“相干性”指代光束的空间相干性。相干性描述了光场空间两点的电场涨落的相关程度，它在决定光场传输特性、光与物质相互作用以及光学成像等方面都起着至关重要的作用［1-6］。对光场相干性的研究，可以追溯到杨氏双孔干涉实验［7］，这一实验对光学的发展意义重大，为相干光学的发展奠定了基础。从杨氏双孔干涉实验以来，人们对光场相干性的研究从未停止。目前为止，光的相干理论经过WOLF E 等的发展，已经形成了一套较为成熟的理论体系［1］。目前可以利用互相干函数和交叉谱密度函数分别描述空间两点在空间-时间域和空间-频率域的相关程度。由于互相干函数和交叉谱密度函数满足波动方程，具有光波特性。因此通过互相干函数和交叉谱密度函数可以对光的相干性实现定量研究。

降低激光相干性可以降低诸多负面影响，但仍无法满足由于人们对激光应用领域的拓宽和深入带来的对激光特性日趋多样化的需求。因此，如何调控激光特性以满足实际需求尤为重要。从对光场相干性调控角度出发，需要设计出一种具有特殊相干性结构分布的新型结构光场，使光场展现出新奇的传输特性以满足人们需求。这里将被降低相干性的光场称为部分相干光场［2］，在过去的几十年中，人们对部分相干光场的研究主要聚焦在高斯-谢尔模光场［8］。其光强分布和相干结构分布均呈现高斯分布。由于构建物理上能实现的具有特殊空间相干结构的新型相干结构光场需要满足一定的限定性条件，因此获得满足这些限定条件的光场相对困难。早期研究者们仅对贝塞尔关联光束和朗伯体光源等有限的几种光束进行研究［9-10］。对于具有其他相干性结构的新型相干结构光场研究的局限限制了该领域的发展。

2007年GORI F 等提出了构建部分相干光场的一个充分条件［11］，使获得描述部分相干光场的数学模型大为简化。基于此项突破性工作，一系列具有不同相干结构的新型相干结构光场的数学模型从理论上相继提出［2-3］。研究表明，通过调控光场空间相干结构可以实现对光场传输特性的调控，例如：自聚焦、自偏移、自愈合、自分裂和自修复等传输特性［3］。总而言之，光场相干结构调控为光场特性调控提供了新的思路，丰富了光场调控理论，为其实际应用奠定了基础。

因此，本文将回顾部分相干光场构建理论，以几类典型的新型相干结构光场为例，重点讨论这几类光束光场模型构建以及传输特性。并归纳总结讨论目前主流的新型相干结构光场实验产生方法。

1 构建新型相干结构光场的非负正定条件

1.1 标量情况

在标量情况下，通过互相干函数和交叉谱密度函数［12］分别表征时间-空间域和空间-频率域中部分相干光场的统计特性。由于交叉谱密度函数在处理包括统计波长在内的相关问题上具有一定的优越性，因此，研究人员逐渐将其作为研究准单色场的首选表征方法。交叉谱密度函数定义为电场空间两点间的相关函数

式中，E表示垂直于传输方向的横截面上的电场函数，r1、r2表示空间任意两点位置矢量，*表示复共轭，尖括号表示系综平均。为了使交叉谱密度函数成为数学上可实现的真实函数，其必须满足的非负正定条件［11］为

式中，p（v）表示任意非负函数，H（r，v）表示任意积分内核函数。在线性系统中，函数H（r，v）可以表示为

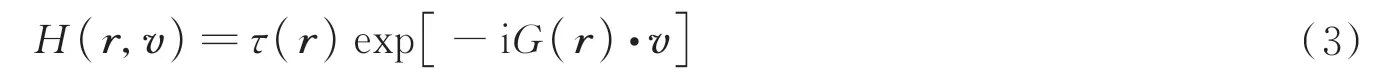
式中，τ（r）表示光场振幅函数，G（r）表示关于空间位置坐标r的实标量函数。将式（3）代入式（2），得

为了定量描述光场在空间两点的统计相似性，引入空间-频率域中的相干函数（谱相干度），表示为归一化的交叉谱密度函数，

结合式（2）和式（5）可以发现，通过调控p（v）和H（r，v）函数，可以构建得到不同的相干函数μ（r1，r2），即构建得到不同种类的新型相干结构光场。

1.2 矢量情况

在矢量情况下，通过相干偏振矩阵和交叉谱密度矩阵分别表征时间-空间域和空间-频率域中矢量部分相干光场的统计特性［13］。部分相干准单色矢量光场的交叉谱密度矩阵可以表示为

矩阵元表示为

式中，Ex和Ey表示随机电场矢量在x和y方向上的两个相互正交分量。为了使交叉谱密度矩阵成为数学上可实现的真实矩阵，GORI F 等在2009年提出了构建矢量部分相干光场的非负正定条件［14］，

式中，pαβ（v）为权重矩阵的矩阵元，

权重矩阵元需满足非负性条件

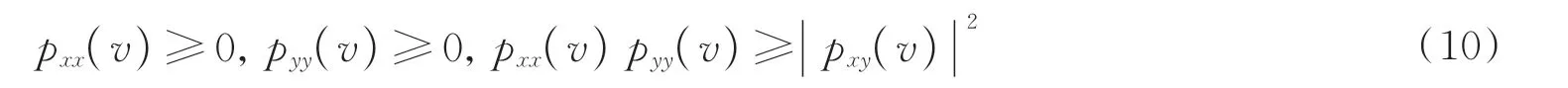
矢量部分相干光场的相干函数可以表示为

因此，通过选取合适的pαβ（v）和Hα（β）（r，v）函数，可以构建得到具有不同相干结构的矢量部分相干光场。值得注意的是，对于矢量部分相干光场的构建产生需要讨论其可实现条件，即，光场的交叉谱密度矩阵须满足准厄米共轭性，。

2 标量新型相干结构光场

上节内容介绍了如何通过非负正定条件构建新型相干结构光场。新型相干结构光场根据其相干结构形式的不同可分为新型均匀相干结构光场和新型非均匀相干结构光场。新型均匀相干结构光场的相干函数只与空间两点位置距离差有关而与两点绝对位置无关，即满足：μ（r1，r2）∝μ（r1−r2）。当相干函数不满足上述条件时，这类新型相干结构光场归类为新型非均匀相干结构光场。为了让读者更直观地了解新型相干结构光场的构建及其奇特性质，本小节将从新型均匀/非均匀相干结构光场分类出发，重点阐述几种典型的新型相干结构光场的相关研究成果。

2.1 新型均匀相干结构光场

当p（v）函数满足高斯分布，且设定积分内核函数H（r，v）中的实标量函数G（r）为空间位置坐标r的线性函数，则可以构建得到的部分相干光场的空间相干结构呈现高斯分布。再设定光场振幅函数τ（r）同样满足高斯分布，可以得到高斯-谢尔模光束［8］

式中，w0表示光束束腰，δ0表示光束相干宽度。关于高斯-谢尔模光束的传输特性已广为人知，因此本文不再详细阐述。相比高斯-谢尔模光束而言，具有特殊相干结构分布的新型相干结构光束会展现一些新奇的传输特性。

2012年，KOROTKOVA O 等提出一种多高斯-谢尔模光束［15］，其选取p（v）函数满足表达式，

式中，k表示波数。将式（13）和式（14）代入非负正定条件式（2），构建得到多高斯-谢尔模光束的交叉谱密度函数

式中μ（r1，r2）表示相干函数

图1 给出了不同光束阶数M的多高斯-谢尔模光束的p（v）函数分布以及远场光强分布。可见多高斯-谢尔模光束的光强在远场呈现平顶分布，并且随着光束阶数M增大，平顶区域随之变大。

图1 多高斯-谢尔模光束性质与光束阶数的关系图，λ=632 nm，w0=1 mm，δ0=0.1 mm［15］Fig.1 Properties of multi-Gaussian Schell-model beams for different beam orders with λ=632 nm，w0=1 mm，δ0=0.1 mm［15］

2015年，CHEN Yahong 等选取积分内核函数H（r，v）依然为式（14）表达形式，而p（v）函数则设定为［16］

式中，G0表示归一化系数，相干函数μ（r1，r2）为

式中，H2m（n）表示2m（n）阶厄米多项式。由于这类光束的相干函数包含厄米多项式，因此，将这类光束命名为厄米-高斯关联谢尔模光束。

图2 展现了不同光束阶数的厄米-高斯关联谢尔模光束的相干度分布图。与高斯-谢尔模光束的相干度分布相比，其表现出阵列分布而非高斯分布，且阵列分布受到光束阶数的影响，光束阶数越大，相干结构的阵列分布越明显。图3 为厄米-高斯关联谢尔模光束在自由空间中的光强演化图，发现厄米-高斯关联谢尔模光束在光源面表现为高斯光斑，随着传输距离的增大，光束从一个光斑逐渐演化成两个光斑，展现出了光束光强自分裂传输特性。

图2 不同光束阶数的厄米-高斯关联谢尔模光束的相干度模方分布图［16］Fig.2 Density plot of the square of the modulus of the degree of coherence of Hermite-Gaussian correlated Schell-model beams for different beam orders［16］

图3 m=0，n=1，δ0x=δ0y=0.2mm 时厄米-高斯关联谢尔模光束在自由空间中光强演化图（m=n=1）［16］Fig.3 Intensity distributions of Hermite-Gaussian correlated Schell-model beams at several propagation distances in free space（m=n=1）［16］

过去的十几年，大量具有均匀相干结构的新型结构光场被构建产生。除了上文中提到的光束，还有圆对称/椭圆对称拉盖尔-高斯关联谢尔模光束、矩形对称/椭圆对称多高斯-谢尔模光束、余弦-高斯关联谢尔模光束、相干阵列光束等。这些光束展现出诸多新奇传输特性，例如：自整形、自分裂、自愈合、自修复等特性。这些特性在自由空间光通信、粒子俘获、光学成像、材料热处理等领域具有重要的应用价值［15-33］。为了本文的精简性，不再详细阐述这些光束的构建和传输特性。

2.2 新型非均匀相干结构光场

本小节介绍新型非均匀相干结构光场的典型。2011年，LAJUNEN H 等选取p（v）函数满足高斯分布，选定的积分内核函数打破了固有的表达形式，创新性地设定了实标量函数G（r）满足空间位置坐标r的二次函数关系［34］，为了计算的简便性，仅给出一维表达式

式中，x0为坐标偏移量。基于如上积分内核函数的设定，构建得到的光束模型表达式为

相干函数μ（r1，r2）的表达式为

从式（22）相干函数的表达式可以看出，这类光束的相干度的值不仅取决于空间两点位置的差值，还与两点位置有关。因此，这类光束被称为非均匀相干结构光束。为了与下文中更复杂的非均匀相干结构光束作区别，这类光束将暂列为传统非均匀相干结构光束。

图4 展现了传统非均匀相干结构光束在自由空间中的光强演化图。从图中可以发现该光束随着传输距离的增加，出现光强自聚焦现象以及最大光强自偏移现象。这与上文中介绍的均匀相干结构光束的传输特性大相径庭。由于非均匀相干结构光束展现出异于均匀相干结构光束的新奇传输特性，随后，大量有关非均匀相干结构光束的工作被相继报道［34-41］。

图4 x-z 方向w0=0.5 mm，δ0=0.5w0传统非均匀相干结构光束的光强演化特性［34］Fig.4 Intensity evolution of conventional non-uniformly beams on the x-z plane with w0=0.5 mm，δ0=0.5w0［34］

观察式（21）可以发现，传统非均匀相干结构光束只有一个相干性参量（相干宽度δ0）。这限制了非均匀相干结构光束的调控能力。基于此因，2018年，YU Jiayi 等将传统非均匀相干结构光束拓展至复杂情况，同时引入新的相干性参量，提出圆对称和矩形对称厄米非均匀相干结构光束［39-40］。其光束模型的交叉谱密度函数表达式分别为

对比式（21）～（24），发现厄米非均匀相干结构光束引入了新的相干性调控参量：光束阶数（m，n）和漂移参量（x0，y0）。下面以圆对称厄米非均匀相干结构光束的传输特性为例进行以下阐述。图5 展现了不同光束阶数的圆对称厄米非均匀相干结构光束在r1－r2平面和x1－y1平面上的相干结构分布。可以看出圆对称厄米非均匀相干结构光束的相干结构分布随着光束阶数的增大，旁斑数量会随之增多，因而将引发众多奇异传输特性。

图5 不同光束阶数下厄米非均匀相干结构光束的相干结构分布图［39］Fig.5 Density plot of the absolute value of the degree of coherence of Hermite non-uniformly correlated beams for different the beam orders［39］

图6 展现圆对称厄米非均匀相干结构光束在大气湍流中的轴上光强和轴上光强闪烁随传输距离的演化特性。文献选取该光束在大气湍流中而不是自由空间中的传输特性作为例子进行阐述：1）圆对称厄米非均匀相干结构光束在自由空间中的光强演化特性和在大气湍流中类似；2）圆对称厄米非均匀相干结构光束在大气湍流中的光强闪烁因子演化与均匀相干结构光束差异巨大，有必要进行相关阐述。从图6 可以发现，圆对称厄米非均匀相干结构光束在自由空间和大气湍流中均表现出良好的光强自聚焦特性，并且可以通过调控光束阶数和光束相干性操控光束自聚焦能力，并且操控光束自聚焦焦点的空间位置：随着光束阶数的增大或相干性的降低，光束自聚焦能力增强，更早出现自聚焦焦点。值得一提的是，圆对称厄米非均匀相干结构光束在适当传输区间内，不仅可以保持轴上高光强特性，而且同时具有较低轴上光强闪烁。这弥补了均匀相干结构光束以牺牲光强强度为代价来降低光强闪烁的弊端，具有重要意义。

图6 厄米非均匀相干结构光束在大气湍流中的轴上光强和光强闪烁演化［40］Fig.6 Intensity evolution and scintillation index of Hermite non-uniformly correlated beams propagation in turbulence［40］

在过去十年内，研究人员也构建产生了一些其他新型非均匀相干结构光场，例如：非均匀拉盖尔-高斯关联光束、非均匀关联贝塞尔光束、伪贝塞尔关联光束、厄米非均匀相干结构阵列光束等。表现出诸多新奇传输特性，例如：自聚焦、自偏移、多焦点阵列以及自聚焦焦点三维空间位置可控特性等［36-43］。

3 矢量新型相干结构光场

在相干光场领域，矢量光场通常分为空间均匀偏振（例如：线性、圆偏振、椭圆偏振）光场和空间非均匀偏振（例如：径向偏振、角向偏振、柱偏振）光场［44］。在部分相干结构光场领域，同样可以把矢量部分相干结构光场分为空间均匀偏振部分相干结构光场和空间非均匀偏振部分相干结构光场。本小节将列举讨论几种典型的矢量新型结构光场的构建及其新奇特性。

3.1 矢量新型均匀相干结构光场

2017年，LIANG Chunhao 等提出一种具有空间非均匀偏振、空间均匀相干结构的新型结构光场——矢量相干晶格阵列光束［45］。权重矩阵和积分内核函数满足

式中，Hα（r，v）表示经由传输距离f，焦距为f的薄透镜以及具有透过率函数为Tα的空间滤波器组成的实际光路传递函数。λ表示波长，Vmn（md，nd）表示离轴位移，d是相邻两个圆域函数的间隔，aαβ表示圆域函数的半径，m和n分别是x和y方向上圆域函数的数量，Bαβ表示x和y方向上电场分量之间的系数。由上述公式以及构建矢量部分相干光束的非负正定条件，得到矢量相干晶格阵列光束，其交叉谱密度矩阵元表达式为

式中，C0表示归一化系数，μαβ（r1，r2）表示相干函数矩阵元

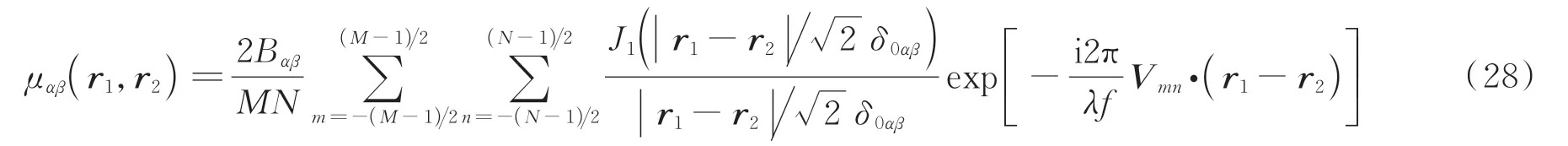
下面以径向偏振作为例子对该矢量新型结构光束进行详细讨论。图7 表示径向偏振相干晶格阵列光束在自由空间中的总光强、分量光强和偏振态随传输距离的演化图。发现径向偏振相干晶格阵列光束的光强分布在光源面展现为单个空心光斑，在传输过程中由于相干结构的影响，光强逐渐演化成阵列分布形式，伴随着偏振态的分布也逐渐呈现阵列分布。

图7 M=N=3，δ0=3mm 径向偏振相干晶格阵列光束在自由空间中传输的光强和偏振态演化图［45］Fig.7 Intensity distribution of radially polarized vector optical coherence lattices beams at several propagation distances in free space［45］

然而上述径向偏振相干晶格阵列光束实际上仅对光场振幅进行矢量调制，并没有实现对相干结构的矢量调制。2014年，CHEN Yahong 等构建得到的新型空间相干径向偏振部分相干光束［46］，实现了对相干结构的矢量调制。权重矩阵元满足

积分内核函数选定同式（26）。通过构建矢量部分相干光束的非负正定条件，得到新型空间相干径向偏振部分相干光束，其交叉谱密度矩阵可表示为

图8 展示了新型空间相干径向偏振部分相干光束相干度模的平方以及相应的相干函数的密度分布图。这种新型空间相干径向偏振部分相干光束的相干度分布与具有传统空间相干结构分布的径向偏振部分相干光束存在很大的差异，它的分布不再是高斯分布。由于相干结构分布的差异，该光束的传输特性与具有传统空间相干结构分布的径向偏振部分相干光束之间也存在很大的差异。具有传统空间相干结构分布的径向偏振部分相干光束的光强分布随着传输距离的增加，逐渐由空心光束演化成高斯分布，而新型空间相干径向偏振部分相干光束的光强演化恰恰相反，由光源面的高斯分布逐渐演化成空心分布（如图9所示）。

图8 新型空间相干径向偏振部分相干光束在光源面的各相干度模方的密度分布图［46］Fig.8 Density plots of different square of the degree of coherence of the novel correlated radially polarized partially coherent beam in the source plane［46］

图9 新型空间相干径向偏振部分相干光束在不同聚焦面上的归一化光强分布图［46］Fig.9 Intensity distribution of the focused novel correlated radially polarized partially coherent beam at several propagation distances［46］

3.2 矢量新型非均匀相干结构光场

对具有非均匀相干结构的矢量部分相干光束的探讨，可追溯到2012年，KOROTKOVA O 等将LAJUNEN H 和SAASTAMOINEN T 在2011年提出的标量非均匀相干结构光场（上节内容已被讨论）拓展至矢量场，提出了电磁非均匀相干结构光束，并通过与众所周知的电磁高斯-谢尔模光束对比讨论了该光场的偏振特性演化规律［47］。紧接着，又详细研究了电磁非均匀相干结构光束在大气湍流中的传输特性［48］。

对于电磁非均匀相干结构光束的构建，需选取权重矩阵和积分内核函数

式中，Ax（y）表示是x（y）电场分量的幅值。Bαβ=|Bαβ| exp(iφαβ)表示α和β方向上场的相关系数，φαβ是两者之间的相位差。rα（β）表示二维离轴位移。根据上述公式以及构建矢量部分相干光束的非负正定条件，得到电磁非均匀相干结构光束的交叉谱密度矩阵

图10 展示了电磁非均匀相干结构光束在场分量不相干时，即，交叉谱密度矩阵中没有非对角分量时，光束的偏振度随传输距离的演化图。图10（a）和（b）分别为最大光强处和z轴上的偏振度演化图。我们发现，与电磁高斯-谢尔模型光束不同，电磁非均匀相干结构光束的偏振度随着传输距离的增加会出现拐点。沿z轴的偏振度曲线出现了更加复杂的演化趋势，出现有多个转折点。这些拐点的出现，从另一个角度也说明电磁非均匀相干结构光束的偏振演化的复杂性。通过对电场非均匀相干结构光束的初始参数调控可以控制光束偏振特性，并可以对其进行灵活横向移动，使其偏振特性的演化不局限于特定的区域。

图10 电磁非均匀相干结构光束随传输距离的演化图［48］Fig.10 Spectral degree of polarization of electromagnetic non-uniformly correlated beams on propagation［48］

2020年，YU Jiayi 等提出一种构建同时具备非均匀偏振和非均匀相干结构的新型结构光束的普适方法，并举例构建了径向偏振厄米非均匀相干结构光束［49］。相对于电磁非均匀相干结构光束而言，这类光束不仅具有非均匀（径向）偏振特性还具有非均匀相干结构特性，文献详细讨论了非均匀偏振与非均匀相干结构的联合调控，促使这类新型相干结构光束展现出更多的物理特性。选取如下构建光束的权重矩阵和积分内核函数

根据上述式子和构建矢量部分相干光束的非负正定条件，得到矢量新型非均匀相干结构光束的交叉谱密度矩阵

图11 径向偏振厄米非均匀相干结构光束在自由空间中光强和偏振态演化图［49］Fig.11 Density plot of the intensity distribution and the state of polarization of radially polarized Hermite non-uniform correlation beams upon propagation in free space［49］

图12 径向偏振厄米非均匀相干结构光束在自由空间中的偏振度演化图［49］Fig.12 Degree of polarization of radially polarized Hermite non-uniform correlation beams upon propagation in free space［49］

2021年，ZHU Xinlei 等提出了一种更为复杂的矢量非均匀相干结构光束［50］，称之为电磁双曲余弦高斯非均匀相干结构光束，构建该光束时选取的权重矩阵为高斯分布形式，即，

积分内核函数Hx和Hy选取为不同的表达形式，这与通常构建矢量非均匀相干结构光束时选取的积分内核函数具有明显的区别

式中，f（r）表示一个实函数，φ0表示x和y方向上的场之间的初始相位差，通过式（40）和构建矢量部分相干光束的非负正定条件，得到交叉谱密度矩阵

式中，

当选取振幅函数τ（r）为高斯分布时，实函数满足f（r）=r2，则构建得到电磁双曲余弦高斯非均匀相干结构光束。电磁双曲余弦高斯非均匀相干结构光束同时具备多种非均匀相干结构光束模式，如图13所示，电磁双曲余弦高斯非均匀相干结构光束的总光强分布为高斯分布，在不同偏振方向上，其光强分量展现出不同的非均匀相干结构光束光强分布，在水平和竖直偏振方向分别表现余弦和正弦非均匀相干结构光束，在45°偏振方向上则表现为传统非均匀相干结构光束。因此，该光束对不同偏振的感应表现出不同的光强分布的特性，在光束整型，光学开关和自由空间光通信中具有重要应用价值。

图13 电磁双曲余弦高斯非均匀相干结构光束在不同偏振方向上的光强分布［50］Fig.13 Spectral density distribution for the electromagnetic cosh-Gauss non-uniformly correlated beam source passing through a linear polarizer with different transmission angles［50］

除了上文中提到的矢量新型相干结构光束，研究人员还构建了许多其他类型的矢量新型相干结构光束。例如：电磁多高斯-谢尔模光束、径向偏振余弦关联谢尔模光束、矢量厄米关联谢尔模光束和径向偏振自偏移部分相干光束等［51-54］。为了本文的精简性，不再详细阐述这些光束的构建和传输特性。

4 新型相干结构光场的实验产生

以上内容主要阐述了构建得到的各种新型相干结构光束的模型，并讨论了新型相干结构引发的各种新奇传输特性。本节将着重介绍两种实验上产生新型相干结构光束的方法。

4.1 基于泽尼克定理产生新型相干结构光场

1979年，SANTIS P 等利用相干光照明旋转的毛玻璃产生非相干光源，并利用准直透镜以及振幅滤波器实验产生高斯-谢尔模光源［55］，利用范西特-泽尼克定理将非相干光源转化为部分相干光源，远场的部分相干光束模型表达式为

式中，a表示与相干宽度有关的参量，f表示准直透镜的焦距。图14 展示了实验产生高斯-谢尔模光束的实验装置图，G 表示旋转的毛玻璃，放置在准直透镜L2的前焦面处。振幅滤波器F 紧贴透镜L2。尽管在旋转的毛玻璃后表面上无法严格产生理想的非相干光，但利用广义范西特-泽尼克定理及传播定律，依然可以得到振幅滤波器后的光束为高斯-谢尔模光束。透镜L3和L4及光电探测器PH 用于探测远场的光强分布。通过控制聚焦透镜L1入射到毛玻璃G 上的光斑大小可以控制高斯-谢尔模光束的相干宽度。

图14 产生高斯-谢尔模光束的实验装置图［55］Fig.14 Experimental setup for generating Gaussian Schell-model beams［55］

2013年，WANG Fei 等基于上述原理，从泽尼克定理出发，结合动态散射体以及光强调制的方法，提出一种产生具有不同空间相干结构部分相干光束的方法［56］。图15 为产生具有不同相干结构部分相干光束的实验装置图。激光入射至空间光调制器（Spatial Light Modulator，SLM），空间光调制器上加载对应不同相干结构的Matlab 计算全息光栅，通过小孔光阑（CA）滤波得到一级衍射光斑经过旋转的毛玻璃将其转化为具有高斯统计特性的非相干光源，再经过准直透镜（L）以及高斯滤波片（Gaussian Approximate Filter，GAF）后得到具有特定相干结构分布的新型相干结构光束。图16 为空间光调制器上所加载的计算全息图及对应产生的椭圆高斯-谢尔模光束和拉盖尔-高斯关联谢尔模光束在焦平面上的光强分布图。

图15 产生具有不同空间相干结构部分相干光束的实验装置图［56］Fig.15 Experimental setup for generating partially coherent beams with different coherence structure［56］

图16 不同关联光束的计算全息图和光强分布图［56］Fig.16 Computer generated hologram and intensity distribution of different correlated beams［56］

2014年，CHEN Yahong 等搭建了一套可以产生新型空间相干径向偏振部分相干光束的实验装置［46］。图17 为实验装置示意图。激光首先经过径向偏振转换器（Radially Polarization Converter，RPC）产生径向偏振相干光束，随后依次通过旋转的毛玻璃、准直透镜及高斯滤波片，最终产生新型空间相干径向偏振部分相干光束。图18（a）展示了这种新型相干结构矢量光束的相干度模的平方μ2（ρ1，ρ2=0）以及相应的相干函数的实验结果图。图18（b）展示了不同初始相干宽度的新型空间相干径向偏振部分相干光束在焦平面上的光强分布。随着光束初始相干宽度的增加，光强分布逐渐从空心分布变成高斯分布。

图17 产生新型空间相干径向偏振部分相干光束的实验装置示意图［46］Fig.17 Schematic diagram of an experimental device for generating novel spatially coherent radially polarized partially coherent beams［46］

图18 新型空间相干径向偏振部分相干光束的相干度模方以及相应的相干函数的分布，光强分布实验结果图［46］Fig.18 Experimental results of the square of the degree of coherence and the intensity distribution of the novel correlated radially polarized partially coherent beams［46］

上述这类方法，主要利用空间光调制器产生特定振幅分布的相干光源，并通过动态散射体得到非相干光源，最后通过传输和振幅调制产生各种新型相干结构光束。该方法优势在于由于快速旋转的散射体，部分相干光束可以快速产生。但由于空间光调制器的能量利用率低以及动态散射体的大量能量损耗，该方法存在的最大缺点就是光源的能量转换率低；且该方法基于范西特-泽尼克定理，仅产生均匀相干结构光束，无法产生新型非均匀相干结构光束。

4.2 基于模式叠加产生新型相干结构光场

基于模式叠加产生新型相干结构光场的方法是从空间相干光源出发，通过随机场的复振幅或相位打破相干性，从而重新构建得到部分相干光束。利用不同的技术手段基于模式叠加产生复振幅屏或相位屏可用于合成新型相干结构光场。

4.2.1 蒙特卡罗谱方法

2014年，KOROTKOVA O 等首先提出理论方法模拟产生传统电磁高斯-谢尔模光束［49］，随后数值模拟得到任意谢尔模型光束的产生［57］。2015年，HYDE IV M W 等通过该方法结合空间光调制器实验产生了任意谢尔模型光束［58］。为了合成具有特定空间相干结构的部分相干光束，可以将式（2）表示成随机场的叠加，其中任意一个随机模式的电场可以表示为

式中，T（r）为复数，表示振幅和相位的随机扰动；S（r）表示谱密度函数。将式（45）代入式（2）可以得到

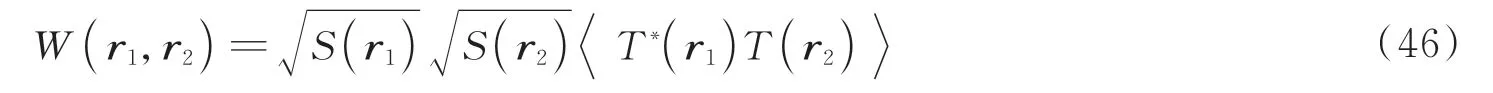
将式（46）与式（5）进行对比，可以发现谱相干度与随机屏的关系，即

当T（r）为均匀分布的随机场时，即合成的部分相干光束为谢尔模型光束。根据维纳-辛钦定理并结合式（47）可以得到

式中，Δr=r1−r2，ΦT表示T（r）函数的功率谱密度函数。从式（48）可以发现它也是相干函数的傅里叶变换，因此可以从已知的相干结构函数反演推出随机相位函数的功率谱密度函数，从而生成随机函数T（r）。

图19 展示了产生任意相干结构谢尔模型光束的实验装置示意图。其中BE 为扩束器，HWP 为半波片，LP 为线性偏振器，SLM 为空间光调制器，加载随机复相位屏对随机振幅及相位的控制实现光场相干结构的调控，L 为透镜，I 为虹膜，BS 为分束器，M 为反射镜，FZC 为远场相机用于远场光斑的拍摄，SPC 为源面相机用于对光源面光斑的拍摄。值得注意的是，实验中对于复相位屏的加载比较困难，早期实验中仅对相位进行了随机调制，后期工作改进了算法实现了复相位屏的调控［59-60］，并进一步拓展算法模拟实现了电磁高斯-谢尔模光束的产生［61］。

图19 利用蒙特卡罗法产生部分相干光束的实验装置示意图［58］Fig.19 Experimental setup for generating partially coherent beams by using Monte Carlo［58］

然而，基于蒙特卡罗法所生成的随机函数是均匀分布的，因此，被认为只能产生谢尔模型光束。近期Hyde 等人利用蒙特卡罗法产生了一类新型非均匀相干结构光束。在生成均匀随机函数的基础上利用映射实现了特定非均匀随机函数的生成，为实现利用蒙特卡罗法产生非均匀关联光束提供了途径［60，62］。

4.2.2 Cholesky 因子分解法

2016，HYDE IV M W 等提出了Cholesky 因子分解法实现实验产生新型相干结构光束［63］。该方法针对任意非均匀相干结构光束的产生，并且将标量光束拓展到矢量光束。他们将随机场写成如下形式

式中，ri是复高斯随机数矢量，R是用Cholesky 分解法分解相干函数的下三角矩阵经由x和y方向上随机场的产生即可产生相应的电磁非均匀相干结构光束。但这个方法对于x和y方向上的相干度选择有其限制条件［64］，仅能产生特定耦合系数的电磁部分相干结构光束。图20 展示了该方法的实验装置示意图，光束经由偏振分束器将光束分成x和y偏振方向上的线偏振光束，分别照射到两台独立控制的并加载随机相位屏的空间光调制器上，最后经由偏振分光器合成电磁部分相干结构光束。Cholesky 分解法计算过程繁琐，需要消耗计算机大量的存储空间以及时间产生相关矩阵的Cholesky，因此，该方法较为繁琐且不够灵活。

图20 产生任意矢量部分相干结构光束的实验装置示意图［63］Fig.20 Experiment setup for generating vector partially coherent source［63］

4.2.3 本征模叠加法

本征模叠加法的原理基于Mercer 展开。式（1）中的交叉谱密度函数可以表示为模式的无穷级数

式中，φn和λn分别表示如下积分函数的本征函数和本征值

式（50）表明，部分相干光束可以由本征模式的非相干叠加实现。2001年，SANTARSIERO M 提出了以正交拉盖尔高斯模式为本征模可实现部分相干涡旋光束的合成［10］。2017年，OSTROVSKY A S 等在实验上用完全正交的贝塞尔模式的非相干叠加实现了一类带有涡旋的部分相干光束［65］。2018年，CHEN Xi 等在实验上实现了拉盖尔高斯模式的非相干叠加产生了部分相干贝塞尔涡旋光束［66］。这类利用正交完备的相干模式的非相干叠加实现部分相干光束的产生方法的实验装置通常由如图21所示［67］。空间光调制器加载可以实现本征模的相应相位全息片，本征值则对应于全息片在空间光调制器上出现的概率。探测器实时采集光强信息，并对一段时间内采集到的不同的模式信息利用计算机进行叠加处理，从而得到部分相干光束的强度信息。本征模叠加的方法需要用到的模式数较少，但受限于部分相干光束的模型，即无法找出任意部分相干光束的模型的本征值与本征模，因此本征模叠加法仅能实现某些特定的部分相干光束的产生。

图21 利用本征模式法产生新型相干结构光束的实验装置示意图［67］Fig.21 Schematic diagram of an experimental device for generating novel coherent structure beam using coherent-mode representation［67］

4.2.4 伪模叠加法

2009年，MARTÍNEZ-HERRERO R 等提出伪模叠加法［68］用来实验合成新型相干结构光束。其原理跟本征模叠加相似，交叉谱密度函数可以表示成

2017年，HYDE IV M W 等提出了一种快速产生部分相干光束的方法［69］。给出一个随机场（相位随机场）

ψ是一个随机数或权重，权重则由概率密度函数P(ψ)决定，其值与光束相干结构函数满足关系式

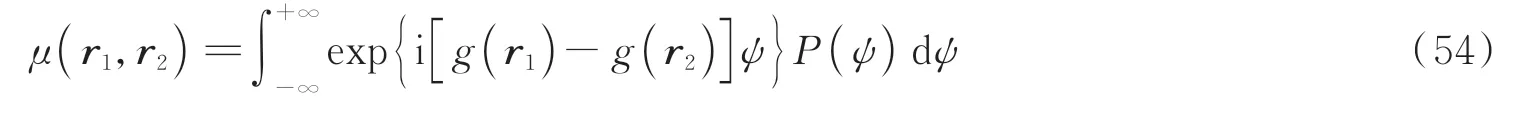
指出部分相干光束可以由式（52）表示的随机场的非相干叠加实现，这与伪模叠加原理一致。利用上述方法实现实验产生传统非均匀相干结构光束［70］。将式（22）拓展至二维并结合式（54），可得出其概率密度函数满足［69］

图22 展示了产生非均匀相干结构光束的实验装置示意图。空间光调制器及变形镜用来加载满足上述概率密度函数的随机场相位ψr2，探测器C 用于接收所产生的光场。实验结果给出了分别用空间光调制器和变形镜产生的传统非均匀相干结构光束，相对空间光调制器而言，变形镜由于具备高速刷新能力，可以实现非均匀相干结构光束的快速产生。

图22 利用空间光调制器或变形镜产生非均匀相干结构光束的实验装置示意图［70］Fig.22 Schematic of the experimental setup for synthesizing non-uniformly correlated sources［70］

伪模叠加法的优势是可以产生具有任意相干结构的部分相干光束。但由于空间光调制器的调制频率较低（60～80 Hz），无法满足相干结构信息的快速调制。变形镜虽然解决了相位屏刷新频率的问题，但却牺牲了像素，无法实现高质量调制。

2020年，ZHU Xinlei 等利用数字微镜器件（调制频率17kHz）实现了一类圆对称非均匀相干结构光束的实验产生［71］。其原理与上述伪模叠加一致，每个伪模可以表示为cn(r，vn) =τ(r)H(r，vn)，每个随机模式出现的概率由Δvp(vn)确定。这里p(vn)表示第n个伪模出现的概率。图23 展示产生这类圆对称非均匀相干结构光束的实验装置示意图。数字微镜器件（Digtial Micromirror Devices，DMD）、透镜（Lens1）、透镜（Lens2）和朗奇光栅（Ronchi-grating）构成了一套4f共轴系统。在这个光路设计中，突破了传统实验中H（r，v）函数的设定，线偏振高斯光束入射到加载振幅光栅的数字微镜器件上，正负一级衍射光束携带g(r)vn+φ0的附加相位，其中φ0表示初始相位。由透镜1 的后焦面上的滤波器滤出正负一级光，再由透镜2 的后焦面的朗奇光栅将两束光束合成。合成后的光场满足

图23 产生圆对称非均匀相干结构光束的实验装置示意图［71］Fig.23 Experimental setup for generation of partially coherent beams with circular coherence［71］

即实现了H（r，v）函数的变换，满足H(r，v) =2cos[g(r)vn+φ0]。由于数字微镜器件的刷新频率可达17 kHz，而探测器的曝光时间为8 ms，因此，探测器仅需拍摄单张图片即可得到合成之后的光斑图，而不需要拍摄多张瞬时光斑后借助计算机叠加产生相对应的光场。整套装置实现了一类非均匀相干结构光束的产生，并且在选定模式数内可实现非均匀相干结构光束的近乎实时产生。

2021年，ZHU Xinlei 等在上述实验装置的基础上实现了矢量电磁非均匀相干结构光束的产生［50］。图24展示了产生矢量电磁非均匀相干结构光束的实验装置示意图。与上述装置不一样的是将滤波器滤出的正负一级光通过在4f共轴系统中加入了1/4 波片分别调制成右旋和左旋圆偏振光束。在由透镜2 后焦面的朗奇光栅将两束圆偏振光合成，合成后的光场满足

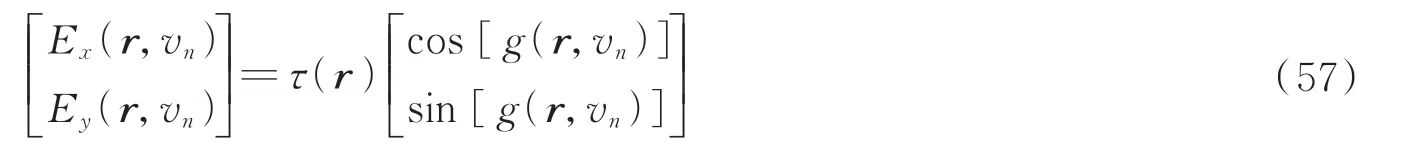
图24 产生矢量电磁非均匀相干结构光束的实验装置示意图［50］Fig.24 Experimental setup for the generation of the electromagnetic non-uniformly correlated beam source［50］

式（57）即实现矢量光场产生的光学系统，其中x方向上的内核函数满足Hx（r，vn）= cos［g（r，vn）］，y方向上的内核函数满足Hy（r，vn）= sin［g（r，vn）］。

与先前产生矢量光场不同的是，数字微镜器件超快的刷新率能够近乎实时地合成矢量新型相干结构光束并且这套4f共轴装置允许精确控制光场中相互正交的两个分量之间的相位差，从而稳定产生矢量新型相干结构光束。该实验装置系统结构紧凑稳定，能灵活合成可用于光束整形，光学开关和复杂环境光通信的矢量新型相干结构光束。

5 总结与展望

本文回顾了新型相干结构光场产生的研究进展，介绍了标量和矢量新型相干结构光场的构建理论基础。分别从均匀相干结构和非均匀相干结构分类出发，列举了几种典型的新型均匀与非均匀关联结构光场案例，分别介绍了这些光束的理论模型和由于新型相干结构引发的新奇传输特性。并总结了实验产生新型相干结构光场的几种方法，包括泽尼克定理法以及模式分解法，其中模式分解法又包含随机模式分解法、相干模式分解法以及伪模分解法，并分别介绍了这几种方法的优缺点。对于新型均匀相干结构光场的理论构建和实验产生已有大量文献发表，而对于新型非均匀相干结构光场的产生，目前报道相对较少，其中一方面原因是由于受到实验条件限制。然而，新型非均匀相干结构光场有着异于新型均匀相干结构光场的新奇传输特性。因此，对不同种类的新型非均匀相干结构光场的构建和实验产生是后续需要关注的研究领域。