产业集群视域下中药材供应链资源共享演化博弈分析*

毛杉珊

（湖南工商大学，湖南 长沙 410000）

1 概述

中药材作为我国传统民族文化资源的重要组成部分，近年来得到了迅速发展，但也迎来了诸如降本增效、协同发展的挑战，而中药材产业集群和协同管理能有效提升中药材供应链的抗风险能力、竞争力及应变能力［1］。加强中药材供应链经营主体间的资源共享有利于促进中药材供应链的协同管理，从而提升中药材供应链的竞争力，推动中药材产业高质量发展。已有文献发现供应链间的资源共享能够明显提升供应链绩效［2-4］，然而现实情况中，内外部资源、市场环境、信任程度等因素都在一定程度上影响着供应链的共享行为［5、6］，供应链间的资源共享与协同合作的内在动力不强［2、3］。鉴于此，很有必要从博弈论的角度出发，对中药材供应链经营主体之间的利益关系及行为动因方面进行针对性分析，帮助中药材产业实现降本增效，提升我国中药材的产业竞争力。由于加工商处于中药材供应链的核心地位［7］，因此文章以中药材供应链中游的加工商为代表，对中药材加工商之间的资源共享演化博弈进行分析，以期为相关产业政策的制定和效果评估提供决策支持。

2 无政府干预的中药材加工商的资源共享演化博弈

2.1 无政府补贴的资源共享博弈模型

首先，下述的中药材加工商的资源共享博弈是建立在非完全理性基础上的长期博弈，且博弈双方的策略组合均为{共享，不共享}。需要说明的是，下文的博弈是发生在中药材加工商已达成长期合作的场景下，即无论加工商双方是否选择资源共享，博弈双方的合作关系依然存在。有关博弈的变量设置和假设情况如下：

π1、π2为加工商1、2不进行资源共享时的收益；B1、B2为加工商1、2选择资源共享时的额外收益，C为加工商选择共享时需要共同承担的成本，∝（0<∝<1）表示加工商1的成本分担比例，∝为定值；如果加工商1、2只有一方选择进行资源共享，则共享方的额外收益Ai，且Ai-αC<0，A2-（1-α）C<0；此时选择不共享的加工商也会由于资源节约获取额外收益，记为Qi。注：上述提到的各变量均为正数，且B1+B2>C，B1-Q1-αC>0，B2-Q2-(1 -α)C>0。中药材加工商资源共享演化博弈的支付矩阵见表1所列。

表1 中药材加工商的资源共享演化博弈的支付矩阵

2.2 无政府补贴的博弈演化路径及结果分析

在这里我们规定：x1、(1 -x1)分别为加工商1选择共享与不共享的概率，x2、(1 -x2)分别为加工商2选择共享与不共享的概率；且0≤x1≤1，0≤x2≤1。设E11、E12分别表示加工商1采取“共享、不共享”的期望收益，E1表示平均收益，由表1可得：

故加工商1的复制动态方程为：

同理，用E21、E22来表示加工商2选择“共享、不共享”的期望收益，E2表示加工商2的平均收益，由表1中的信息可得：

故加工商2的复制动态方程为：

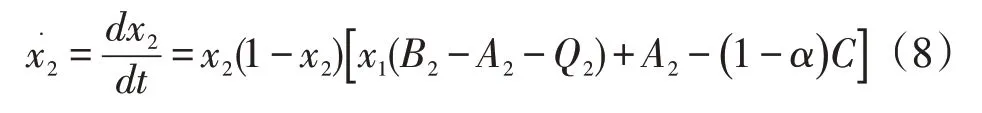
通过计算方程（4）、（8）得到，该博弈系统中存在E1（0，0），E2（0，1），E3（1，0），E4（1，1），E5（x1，x2）这5个平衡点，其中已知博弈系统的平衡点，下一步需要判断平衡点的稳定性，这里我们根据Friedman［8］的方法，借助雅克比（Jacobian）矩阵的局部稳定性来推断出平衡点的稳定性。由复制动态方程（4）、（8），不难得出系统的雅克比矩阵为：

博弈系统的平衡点是演化稳定点需要同时满足以下两个条件：一是矩阵J的迹小于0，二是行列式| |的值大于0。系统的平衡点E1（0，0），E2（1，0），E3（0，1），E4（1，1），E5（x1，x2），其 中的局部稳定性为：稳定点——E1（0，0），E4（1，1）；不稳定点——E2（1，0），E3（0，1）；鞍点——E5（x1，x2）。

因此，此时系统的演化稳定平衡点为E1（0，0），E4（1，1），演化稳定策略（ESS）为（加工商1不共享，加工商2不共享）和（加工商1共享，加工商2共享）。通过分析可以得出：

（1）在上述构建的中药材加工商横向资源共享演化博弈系统中，经过长期博弈系统只会出现双方均共享与均不共享两种结果。最终的博弈结果如何取决于初始点落在博弈相图的哪个区域，如图1所示。若初始点落在四边形E1E2E5E3内，系统将朝点E1（0，0）收敛，即双方均选择不共享；若初始点落在四边形E2E4E3E5内，系统将朝点E4（1，1）收敛，即双方均选择共享。

图1 中药材加工商资源共享演化博弈相图

（2）如果SE1E2E5E3=SE2E4E3E5，那么P共享=P不共享；如果SE1E2E5E3>SE2E4E3E5，那么P共享P不共享。

3 政府补贴下的中药材加工商的资源共享演化博弈

由上述的分析已知，假若初始点落在四边形E1E2E5E3区域内，中药材加工商均会选择资源不共享，此时明显不利于发挥中药材加工商的协同效应，不利于中药材产业的集群发展，因此需要通过政府的干预促使加工商积极进行资源共享。

3.1 政府补贴下的资源共享博弈模型

假定中药材加工商对资源共享持积极态度时，会带来正向的外部效应，在此种情况下政府会采取一定的扶持措施来引导该种行为，如政府补贴，在这里我们用M表示补贴力度，其他变量情况同上，那么加工商1、2的收益矩阵见表2所列。

表2 政府补贴下的中药材加工商的资源共享演化博弈的支付矩阵

3.2 政府补贴下的博弈演化路径及结果分析

假设政府补贴情况下，加工商1选择资源共享与不共享的概率分别为y1、(1-y1)，加工商2选择资源共享与不共享的概率分别为y2、(1-y2)；且0≤y1≤1，0≤y2≤1。设加工商1采取“共享、不共享”的期望收益分别为，平均收益为，由表2中的信息可得：

故此时加工商1的复制动态方程为：

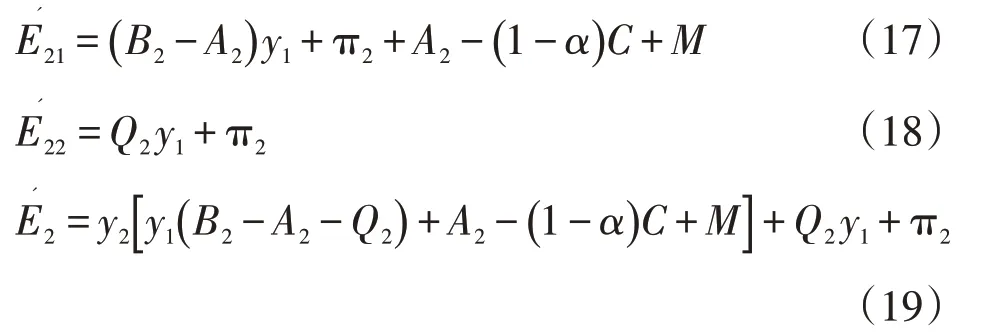
故此时加工商2的复制动态方程为：

同上，根据上述的复制动态方程（16）和（20），计算得出系统的雅克比矩阵J=，其中：

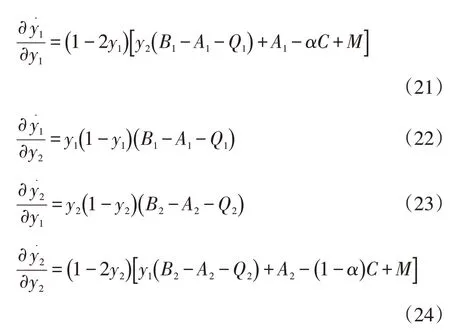
令1=αC-A1，2=( )1-α C-A2，通过判断矩阵的行列式和迹的值的正负可知系统的平衡点O（0，0），）的局部稳定性如下：

（1）当M>max{1,2}时，系统平衡点的局部稳定性为：稳定点——C（1，1）；不稳定点——O（0，0）；鞍点——

（2）当M

由上易知：当政府补贴M>max{αC-A1,(1 -α)C-A2}时，系统只存在一个稳定点（1，1），此时加工商1、2均选择进行资源共享，有利于中医药产业的集群发展。

4 结论

文章建立了以中药材加工商为代表的中药材供应链横向资源共享演化博弈模型，探讨满足什么条件时中药材加工商资源共享长期博弈结果趋向收敛到{共享，共享}，通过分析中药材加工商资源共享演化博弈过程得出以下结论：

（1）在政府不干预的情况下（即无政府补贴时），通过构建分析中药材加工商的资源共享演化博弈模型发现，系统中存在（共享，共享）以及（不共享，不共享）2个均衡点，同时最终的均衡点如何由各个影响参数的初始值决定。

（2）当在中药材加工商资源共享演化博弈模型中加入了“政府补贴M”这一因素时，得出当M>max{αC-A1,(1 -α)C-A2}时，系统只存在1个演化均衡（共享，共享）。此时，博弈双方均选择资源共享，系统达到帕累托最优。