基于动力系统分数阶PI（FOPI）控制永磁同步电机调速系统的对比研究

付雪松

（甘肃省中医院 设备管理处，甘肃 兰州 730050）

0 引言

传统的动力系统主要使用无刷直流电机，其运行时具有相应的励磁电流，并且功率因数小、力矩惯量比小、效率较低。而永磁同步电机具有体积小、损耗小、构造简单，启动转矩大、工作可靠、调速性能好、效率高，没有换向器和电刷等特征。基于PMSM模型，使电机驱动系统具有较大的启动转矩及功率过载能力，同时也具有较高的系统控制精度、频繁启停及反复运动的能力和较好的动态抗扰性能。综上，研究高精度控制算法来控制永磁同步电机，将整数阶PI控制器替换为分数阶PIλ控制器，使其满足动力系统对电机驱动系统响应快、位置控制精度高、无振动的性能要求。

1 方法

1.1 PMSM模型建立

为了使动力系统达到多输入、强耦合、非线性系统的要求，对永磁同步电机的数学模型提出以下要求：首先启动转矩低，没有滞回损耗和沟槽效应，噪音低；其次，转子与定子间无径向力；最后，在电机高速运转时，电感值要很小，这使得电机启动电压低，同时降低电机的重量，提高功率密度。

对所研究的电机作如下假设：（1）忽略永磁同步电机铁芯的饱和；（2）不计永磁同步电机中的涡流和磁滞损耗；（3）转子上无阻尼绕组；（4）永磁同步电机的电流为三相正弦波电流。

电动机的数学模型由电压方程、磁链方程、转矩方程和运动方程组成。

电压方程：

磁链方程：

转矩方程：

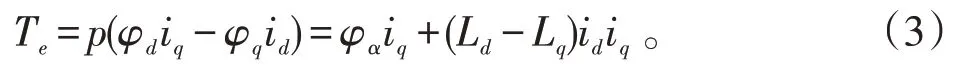
运动方程：

在电机的分析和控制中，首先要对其模型进行解耦，通过a、b、c三相静止坐标系、∂-β静止坐标系和d-q旋转坐标系进行相应变换。在坐标系转换中，前后磁动势和转速严格不变，才能够把将两种坐标等效。d、q轴以角速度ω1逆时针旋转时，对两绕组加直流电压Ud、Uq，产生旋转的磁动势F，F和α、β轴坐标等效。d轴和α轴的夹角随d-q坐标系旋转而改变。

综上可得：

当三相电流不平衡时，每相电流中都含有相同的零轴分量i0，定子三相绕组完全对称。只要是一个平衡对称系统，无论三相电流是否对称，且永磁同步电机中心不接地，则有：

永磁同步电机相关参数如下：额定电压UN=560 V，额定转速nN=5 000 rad/min，定子电阻R=2.875ω，交轴电感Lq=0.009 H，直轴电感Ld=0.008 5 H，转动惯量J=0.008 kg·m2，转子永磁磁链ψr=0.2 Wb，主转子极对数p=4（对）。

1.2 PI控制

速度调节器可以使转速n快速跟随给定的电压而变化，这是速度调节系统中的主调节器。采用（广义）PI调节器，可实现无静差调速；输出的限幅电流限制了电动机的最大允许电流，同时对负载变化的影响起到良好的抗干扰作用。在调节外环速度的同时，其作用是使电流紧密跟随其给定电压即外环调节器的输出而变化，对电网电压的波动进行抑制，起到抗干扰作用。当电机过载甚至堵塞时，将最大电枢电流做一个限幅，在保护电机的同时还能起到快速准确的自动调节作用。当故障消失后，系统可以较稳定地恢复到正常运转，加快了动态过程。

如图1所示，ACR为电流环控制器，比例参数为kcp，积分参数为kci，采样时间为10-6s，τi是调节器的超前时间常数，输出上下限为650、-650，输出电流环的控制对象是两个时间常数相差较大的双惯性控制对象，采用PI型的电流调节器；ASR为速度环控制器，ksp设置为比例参数，ksi设置为积分参数，采样时间同样为10-6s，tn是调节器的超前时间常数，输出上下限为10、-10。

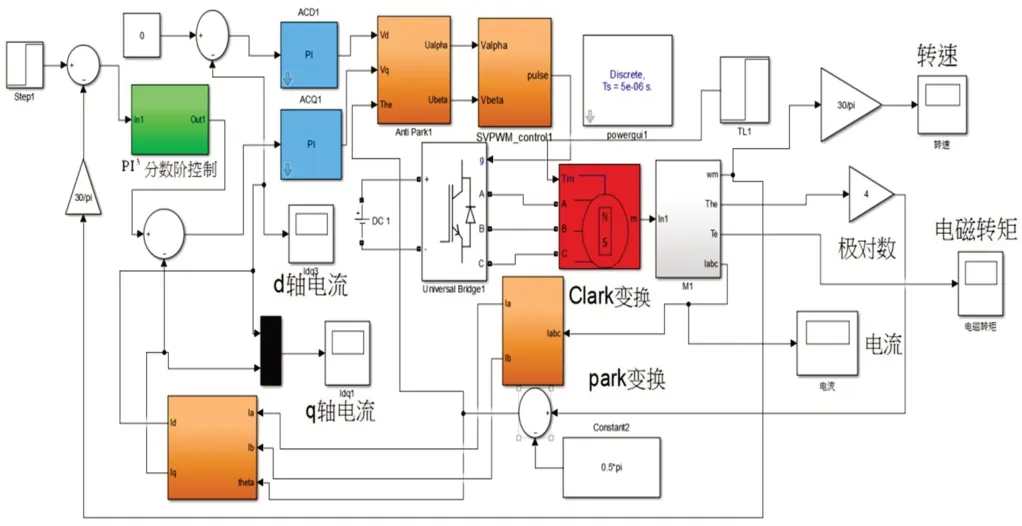
图1 PI控制系统

经计算，取ASR转速环PI控制器中Kp=0.1、Ki=2。

1.3 分数阶控制

分数阶控制器理论和PID控制器整定理论融合后，开辟了一个新的研究方向。这个分数阶控制器的一般格式为PIλDμ，取λ阶积分，μ阶微分，相比于一般PID控制器，多了2个可整定的参数。当这些阶次取分数时，即不是传统意义上的微积分。

分数阶PIλDμ控制器相对于整数阶PID控制器来说，增加了2个可调参数λ和μ，作为不同的微积分阶次，其结构如图2所示。

图2 分数阶控制器

分数阶PIλ控制器运用到速度控制环中，取得了较好的控制效果。由于分数阶PIλ控制器中引入了积分阶次λ，使控制器参数的选取范围变得更加灵活。本论述未涉及微分及其阶次μ，下文不再赘述。

分数阶控制器参数设置是设计研究中非常重要的部分，各种参数的选择和计算直接关系到控制器的控制效果。各种参数对分数阶系统的影响：首先，Kp为比例项，它可以对放大控制器输入值的误差进行一定放大，用于误差灵敏度的调节。如果增大比例系数Kp，可对出现的误差做出更为迅速的反应，从而加快系统的整体响应速度；其次，积分项Ki的主要作用是在系统进入稳态后，对其进行调节。当系统存在一定的稳态误差时，由于积分项的累加性质，输出误差逐渐减小，最终减小到0，从而提高了系统稳定的精度；Ki值的大小直观地反应出了积分作用的强度，如果积分作用太弱，对系统的影响就会太小，增加系统消除静差的时间，而作用过大可能会导致系统的不稳定，故Ki的大小对系统性能的影响有着两面性。对于分数阶次λ，使用滤波算法程序，进行如下化简：

算法中参数为：λ、N、ωω、T，l表示分数阶的阶次，N为所需逼近的精度，ωω表示拟合频率的上下限。由于算法可能具有一定的局限性，选择ωb·ωh=1。

按照上述理论设计分数阶模块，同时进行控制变量使得Kp=0.1，Ki=2，与PI控制中参数相同。Fractiona模块是将滤波算法的M文件进行调用，加入一个Saturation模块，目的是将输入信号限制在饱和上限和下限。

分数阶次为l，下文将对其取值进行仿真研究；逼近阶设置为0.92；频率范围满足ωb·ωh=1。分数阶仿真同样采用id=0的控制策略。

2 结果

2.1 PI控制阶跃响应结果

经仿真后，PI控制阶跃响应曲线如图3所示，电磁转矩波形如图4所示。

图3 PI控制阶跃响应曲线

图4 PI控制器阶电磁转矩波形

2.2 PI分数阶控制阶跃响应结果

通过上述计算得l=-0.01，在MATLAB中运行该程序，并在Simulink中仿真后，得响应曲线如图5所示，电磁转矩波形如图6所示。

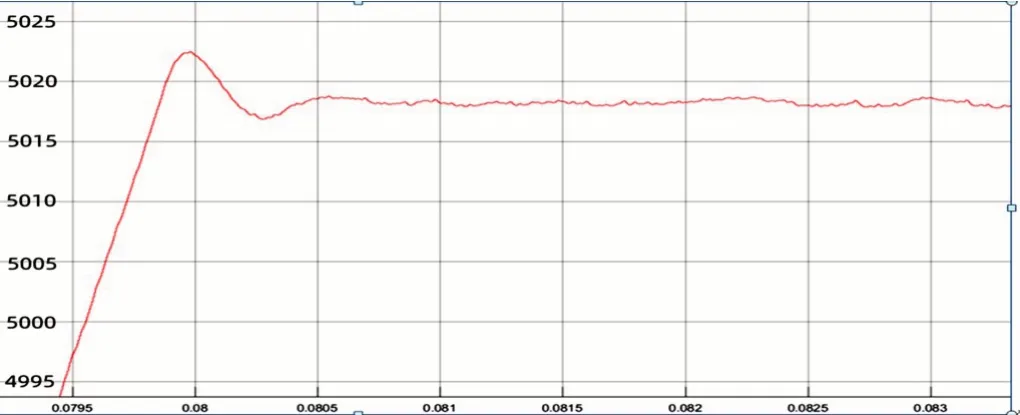
图5 分数阶控制阶跃响应曲线

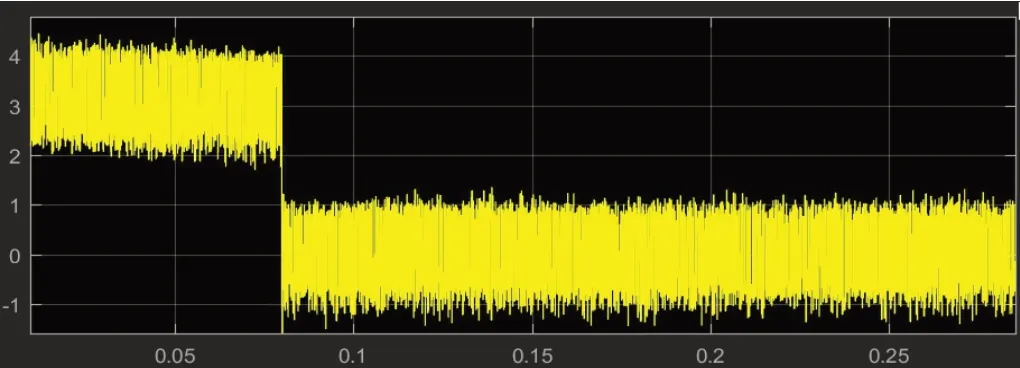
图6 分数阶控制电磁转矩波形

3 讨论

3.1 PI控制分析

PI控制仿真数据如图7所示。

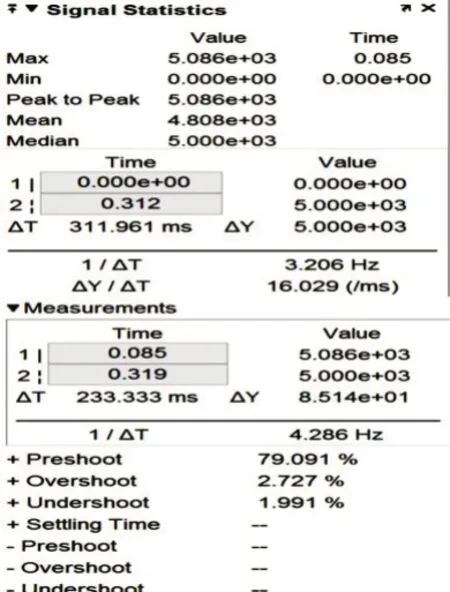
图7 PI控制响应数据

经过仿真计算，转速最大值为5 086 rmp，上升时间为0.085 s，最大转速到给定转速的调节时间为233.333 ms，超调量为2.727%，转速从0到稳定在5 000 rmp的时间为311.961 ms。电磁转矩在电机启动时间较大，在0.1 s以后，逐步趋于稳定，表明电机转速稳定在5 000 rmp。三相电流在启动时较大，运行在-10～10，当转速趋于稳定时，电流减小，运行在-3～3。d轴电流基本稳定在0附近，符合预设控制策略，这就保证了输出转矩最大化，且只与定子电流（iq）的幅值成正比。

由于反电动势代表了转速输出对电流环的影响，它与转速成正比关系。通常系统的电磁时间常数Tl远小于机电时间常数Tm，所以电流环的变化比转速环快得多，而且反电动势对电流环来说，是个较慢的扰动。综上，在电流的瞬时变化中，反电动势基本不变。

3.2 分数阶控制分析

分数阶控制响应数据如图8所示。

图8 分数阶控制响应数据

经过仿真计算，数据结果如图8所示。分数阶控制转速最大值为5 022 rmp，上升时间为0.08 s，转速从0到稳定在5 000 rmp的时间为1s，尽管相比PI控制的311.961 ms延长到了1 s，但超调量为0.909%。电磁转矩在电机启动时间较大，在0.1 s以后，逐步趋于稳定，表明电机转速稳定在5 000 rmp。三相电流在启动时较大，运行在-10～10，当转速趋于稳定时，电流减小，运行在-3～3。d轴电流基本稳定在0附近，符合预设控制策略，这就保证了输出转矩最大化，且只与定子电流（iq）的幅值成正比。通过对比电磁转矩波形，可以看出较PI控制，电机的启动转矩波形更为规则连续，突变程度小，更快趋于稳定，使转矩更紧凑地保持在0附近。

两种仿真均采用的是id=0的控制策略。这是一种转子磁链定向控制，实现较为容易。因为电枢反应中，直轴部分没有产生去磁分量和去磁效应，所以没有出现退磁而损坏电机。对于永磁同步电机来说，id=0的控制即为最大转矩电流比控制。由转矩公式可以看出，永磁同步电机在运行过程中，保证id=0，使定子电流产生的电枢磁动势与转子励磁磁场间的角度为90°，且只与定子电流（iq）的幅值成正比，这就保证了输出转矩可以达到最大值。

当l增大时，系统的超调量相应减少，稳定性持续提升，但是上升时间变长。l过大时，系统将出现失控，稳定性差。l减小时，系统的调节时间会变长，但是响应速度比较快。因此，要使系统的动态性能较好，l的值需合适。当l=-0.001时，超调量在3次实验中最小，调节时间最短，系统稳定性最好，所以将l定为-0.001。转速最大值为5 006 rmp，上升时间为0.08 s，此时超调量仅为0.12%。

将该动力系统两种控制模式应用于切割骨模型实验。对材质、形状等参数相同的两块骨模型同时进行切割，完成后利用3D激光测量显微镜观测铣削加工后的骨模型表面质量以及利用LEXT软件测量铣削槽进给方向上的线粗糙度，两种控制下的切削表面形貌模型如图9所示。

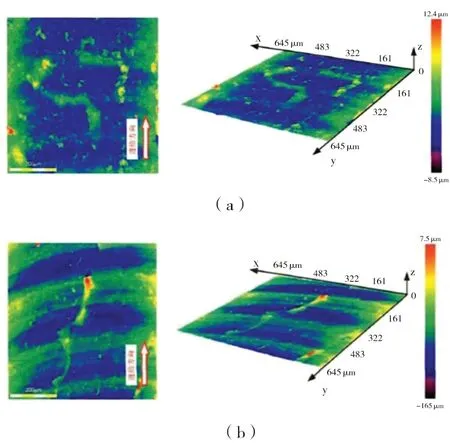
图9 切削表面形貌模型

图9（a）为PI控制下的切削表面形貌，其表面有不同程度的凹凸以及积屑产生；图9（b）为分数阶控制下的切削表面形貌，切削纹理清晰可见，有明显的切削纹理方向。由此可以得出，不同的控制系统，切削表面质量明显不同，分数阶控制系统的切削情况更为理想。

接下来，对分数阶控制进行优化。经计算，如图10所示：中由上到下依次为红线l=-0.01、紫线l=-0.007、蓝线l=-0.001。当l增大时，调节时间逐渐减少，跟踪加快，波形更加平稳，快速趋于稳定。

图10 l取不同值时分数阶控制阶跃相应曲线

4 结论

两种控制模式主要性能参数对比见表1所列。

表1 两种控制模式参数对比

表1分别对两种情况下的仿真曲线及其特性曲线参数作了对比，直观地反映出了后者较前者而言更为理想，与本论述研究结论一致。两种情况相比较，分数阶控制的超调量较PI控制减少了2.067%，上升时间下降了0.005 s，基于更加稳定的响应，调节时间却延长了688.039 ms。

如图11所示，P、I参数相同的情况下，将分数阶控制参数l设置为-0.01，使两种控制方法同时实现。首先PI控制的超调量远高于分数阶控制，高达2.067%；其次，在稳定性方面，分数阶控制很快就稳定在给定的5 000 rmp。整数阶在相比之下，恢复稳定所需要的时间大大延长，分数阶整定控制的优势非常明显。综上，分数阶PIl控制器的3个参数整定为Kp=0.1、Ki=2、l=0.001。

图11 P、I参数相同整数阶与分数阶阶跃响应曲线比较

通过对比，对动力系统的电机进行替换并采取分数阶调速控制，从分数阶积分项sλ的特性可以看出，通过不断改变该项取值，分数阶积分项越小，它对系统的影响表现为较强的比例作用和较弱积分特征。同样分数阶积分项越大，就导致越偏向分数阶积分多一些，故对其影响越大，该系统将表现出积分较强但比例较弱的特点。最终，使超调量、调节时间减少，电机运转更加稳定，响应迅速，获得更为理想的控制效果。

考虑到各种各样的阻力和扰动，所以在电机的控制仿真时，假设在第0.5 s时同时给两种控制模式下的电机Tm输入端加入负载扰动，此时响应曲线如图12所示。

图12 加入扰动后两种控制响应曲线

可以看出在受到同样的扰动后，二者皆有一定程度的偏离。图12中红色曲线为分数阶控制响应。在受到扰动后，转速响应曲线在发生很小的下降后以极快的速度使电机趋于稳定运行；而整数阶PI控制，先经过很大的下降波动，才较为缓慢地恢复稳定。

对分数阶控制器基于滤波算法、期望的幅值裕量Am和相位裕量φm设计最优PIλ控制器。经过分数阶近似优化，计算调节该模型的分数阶控制器的阶次，得到不同的转速响应结果。选择系统阶跃响应动、静态特性相对最好的曲线，从而确定最后的分数阶模型。

我国动力系统方面的发展刚刚起步，技术尚不成熟，相关研究资料及文献较为匮乏，目前国内市场上多为动力系统的维修、保养。底层核心技术主要还是以国外引进为主，缺乏国内的创新与研发，本论述正是基于此，对动力系统的核心进行了研究。