基于Res3dinv软件的三维高密度电法成像效果分析

王 钧，朱国维

(中国矿业大学(北京) 地球科学与测绘工程学院，北京 100083)

1 引 言

高密度电法是当前应用较广的浅层地球物理探测技术，三维高密度成像数据主要是通过布设的多条二维测线数据平移合并或真三维观测系统采集完成[1]。在实际的地质体探测中，关注较多的是可能存在的异常体空间定位与分布范围，而不仅仅是一条测线反演出来的某个剖面或多剖面的简单叠加[2]。当前三维高密度电法的探究使用已经较为广泛，施龙青等将三维高密度电法应用于底板与顶板的含水探测中，克服了二维情况下只能获取巷道底板和顶板电阻率而不能得到地质体内部电阻率分布特征的缺点[3,4]。黄俊革等使用E-SCAN电极布设方式对常见的地质体进行模拟，得到了低阻异常响应较好的结果，建议先用此方式测量区域的面积，以此确定可能存在的异常体范围，再反演出纵向的位置特征[5]。黄真萍等将三维高密度电法用于各种地电模型，提出了反演体积效应的假象问题，认为这种方法对于异常体有较好的分布探测能力，但要综合考虑存在的干扰因素[6]。高阳等在岩溶塌陷区使用三维高密度电法探测技术，获得了岩溶地质体立体分布的尺寸范围，表明此方法对于常规电法存在的体积与旁侧效应有一定的减弱能力[7]。朱瑞等在拟建水库坝区开展三维高密度电法地质情况探测，并结合现场钻孔资料验证方法的可靠性，提出了为避免多解性问题，应采取综合探测分析方法[8]。张先林等通过时移三维高密度电法对黄土层灌溉水入渗方式进行研究，并通过Voxler软件将反演结果进行成像处理，得到了试验区的入渗过程与对应规律[9]。本文将三维高密度电法正演软件Res3dmod的模拟结果导入反演软件Res3dinv中进行计算，然后结合Matlab程序实现了可视化反演成像，并分析了成像效果，得到了各因素变化带来的响应特征及规律，最后根据实例的Voxler软件成像结果讨论了所对应的实际地质情况。

2 方法原理

高密度电法基于可能潜在的目标地质体与周围岩土层的电阻率差异来进行探测分析，通过观察人工建立的地下稳定电流场的传导分布规律来获取对应地区的地质情况(图1)。在三维笛卡尔坐标系下，假设任一点(x0,y0,z0)处电流为+I，则有[10]：

(1)

=∇·( [σ]∇ [U] )

(2)

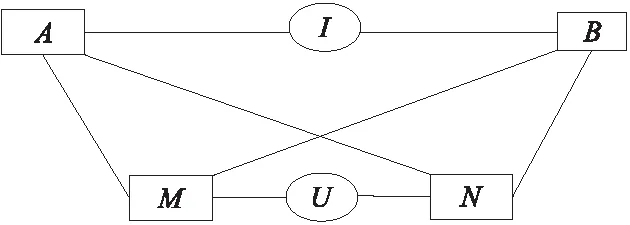
图1 电阻率法电极连接Fig.1 The electrode connection of resistivity method

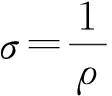
(3)

ρ为电阻率(Ω·m);K为装置系数;A、B为供电电极;M、N为测量电极。由于实际工作需要，选择A、B、M、N的相对位置来设置探测装置，现场探测得到的电阻率受多因素的影响，因此其为视电阻率[14]，例如图2的单极-偶极装置[15]：

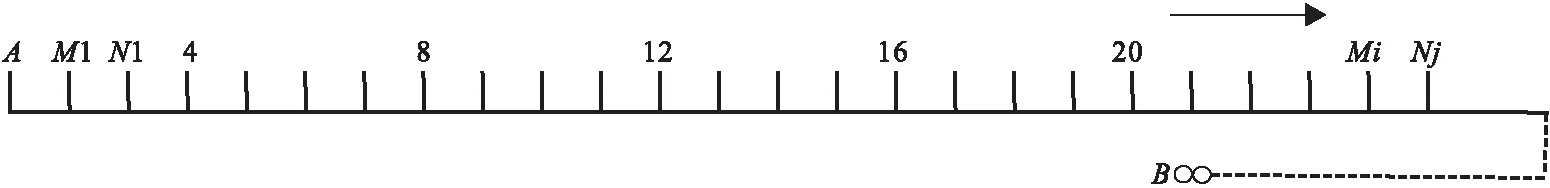
图2 单极-偶极装置示意图Fig.2 The schematic diagram of pole-dipole device

此时，测量的视电阻率

(4)

其具有较高的横向分辨率，采用单极供电方式，结果与其他装置间具有转换性[16]。

2.1 有限差分法

在实际计算中，可以将电场的总电位U总表征为正常场U正与异常场U异之和[17，18]，正常场可根据解析方程式求解：

(5)

异常场通过有限差分法迭代求解，有限差分主要依据泰勒级数展开等数学近似手段，以点差商代替点微商，其可以采用向前、向后，以及中心差分格式。以中心差分交错网格为例，2M阶精度为：

(6)

式(6)中，Cm为对应差分系数，将此格式代入式(2)中即可得差分控制方程。可以将全部结点建立的差分控制方程写成矩阵形式[19]：

[C]·[U]=[Q]

(7)

式(7)中，[C]是差分方程的系数矩阵，与地层电阻率相关；[U]是节点的电位矩阵；[Q]为给定地质体分布及边界后的常向量。计算式(7)即可得到电位的空间点值。下文的模型一至九采用此方法。

2.2 有限元法

有限元是运用变分的方法将微分方程边值求解换成泛函极值求解，进而将求解区域划分为各个子单元，建立插值函数与数值积分形式进行单元的集成迭代求解(图3)。其能够处理不规则模型，如下文的起伏地形模型十和十一。

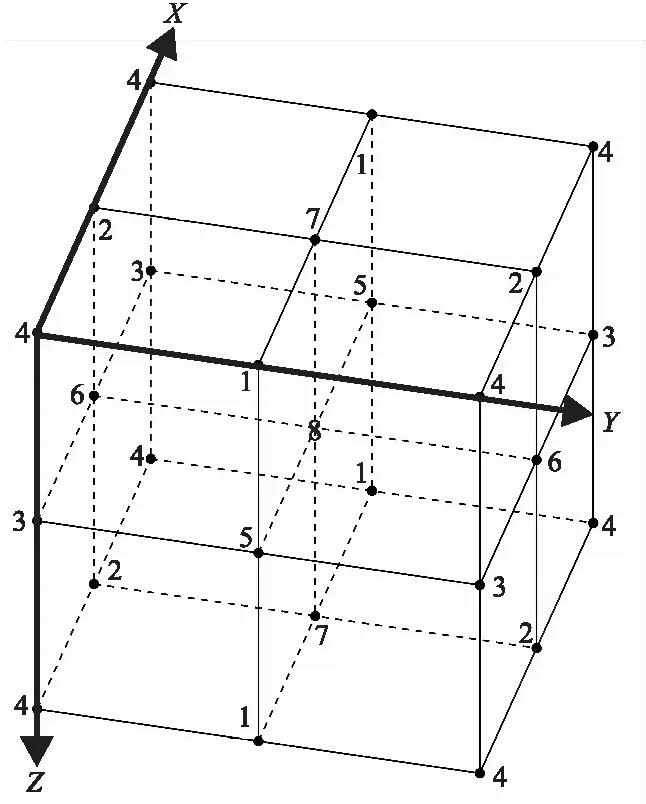
图3 网格分布示意图Fig.3 The schematic diagram of grid distribution

此方法针对的变分问题可以表述为式(8)[20]：

式中，Ω表示区域;Γ为边界向量;n指向边界外法线;r为电源点到边界点的距离。

2.3 光滑约束最小二乘法

在三维电阻率数据的反演过程中，常采用光滑约束的最小二乘优化方法，能够有效降低模型与实测数据之间的差异。三维光滑约束最小二乘法基于以下方程[21]:

(JTJ+λF)Δqk=JTg-λFqk

(10)

(11)

式(10)和式(11)中，Cx、Cy是水平光滑滤波系数向量，Cz为垂直光滑滤波系数向量；J是雅克比偏微分向量，JT为J的转置向量；λ为阻尼因子；q为模型扰动向量；g为偏差向量。

3 模型与算例

以单极-偶极装置为例，X方向电极数为39个、Y方向电极数为11个，各方向电极距为1 m，即X方向探测区间为0～38 m、Y方向探测区间为0～10 m。采用的模型电阻率值分别有低阻值20Ω·m、背景值100Ω·m，以及高阻值1 000 Ω·m。正演建模时网格划分为9层：第1层(0～0.47 m)；第2层(0.47～1.09 m)；第3层(1.09～1.84 m)；第4层(1.84～2.66 m)；第5层(2.66～3.47 m)；第6层(3.47～4.68 m)；第7层(4.68～6.08 m)；第8层(6.08～7.49 m)；第9层(7.49～9.01 m)。带地形反演的结果模型有10层，其余模型反演结果均为13层，最大探测拟深为13.2 m，取8个不同深度面进行三维可视化成像。

如图4所示，模型一异常体设定在3、4、5层；模型二异常体设定在4、5、6层；模型三异常体设定在5、6、7层，平面尺寸均为3 m×4 m。可以看到模型一电阻率中心值深度位置从0.97～3.03 m，模型二电阻率中心值深度位置从1.56～3.94 m，模型三电阻率中心值深度位置从2.25～6.18 m，反演中心位置出现一定偏差，但延伸范围基本能说明异常体的存在影响区间。其中处于较低深度的异常体反演形状边界清晰，而处于较深位置时异常体反演形状边界发生变形，由于高低阻间的响应相互影响，出现了一定的电阻率过渡区域，且随着深度的增加，体积效应越发明显，说明了高密度电法浅层的适用性，而在深层需要注意体积发散的假象。

如图5所示，模型四与模型五异常体均设定在3、4、5层，其中模型四低阻体平面尺寸为2 m×2 m，高阻体平面尺寸为2 m×4 m；模型五低阻体平面尺寸为4 m×4 m，高阻体平面尺寸为4 m×8 m。可以看到，对于浅层同一深度不同尺寸异常体响应的效果一致，区别在于扩散假象与高阻体尺寸大小呈正相关，而与低阻体尺寸大小呈负相关。方形的高阻体对浅层与深层的扩散影响较多。

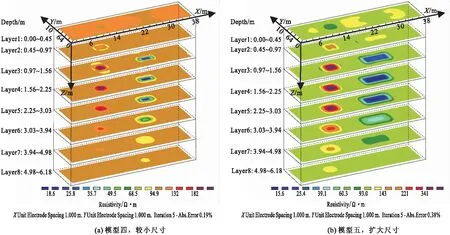
图5 模型四、五尺寸大小反演结果Fig.5 The size inversion results of models 4 and 5

如图6所示，模型六和模型七的异常体电阻率值与模型四和模型五相反，扩散假象的认识与上述分析一致，方形的低阻体尺寸扩大后对浅层与深层扩散影响变得较多，综合模型四、五、六、七可见，异常体X向与Y向的扩展比例也是成像的一个影响因素，体现出形体的延伸响应特征，尺寸变大后等距异常体产生了更大的影响，反映了异常体不同边距比的抗干扰能力不同。

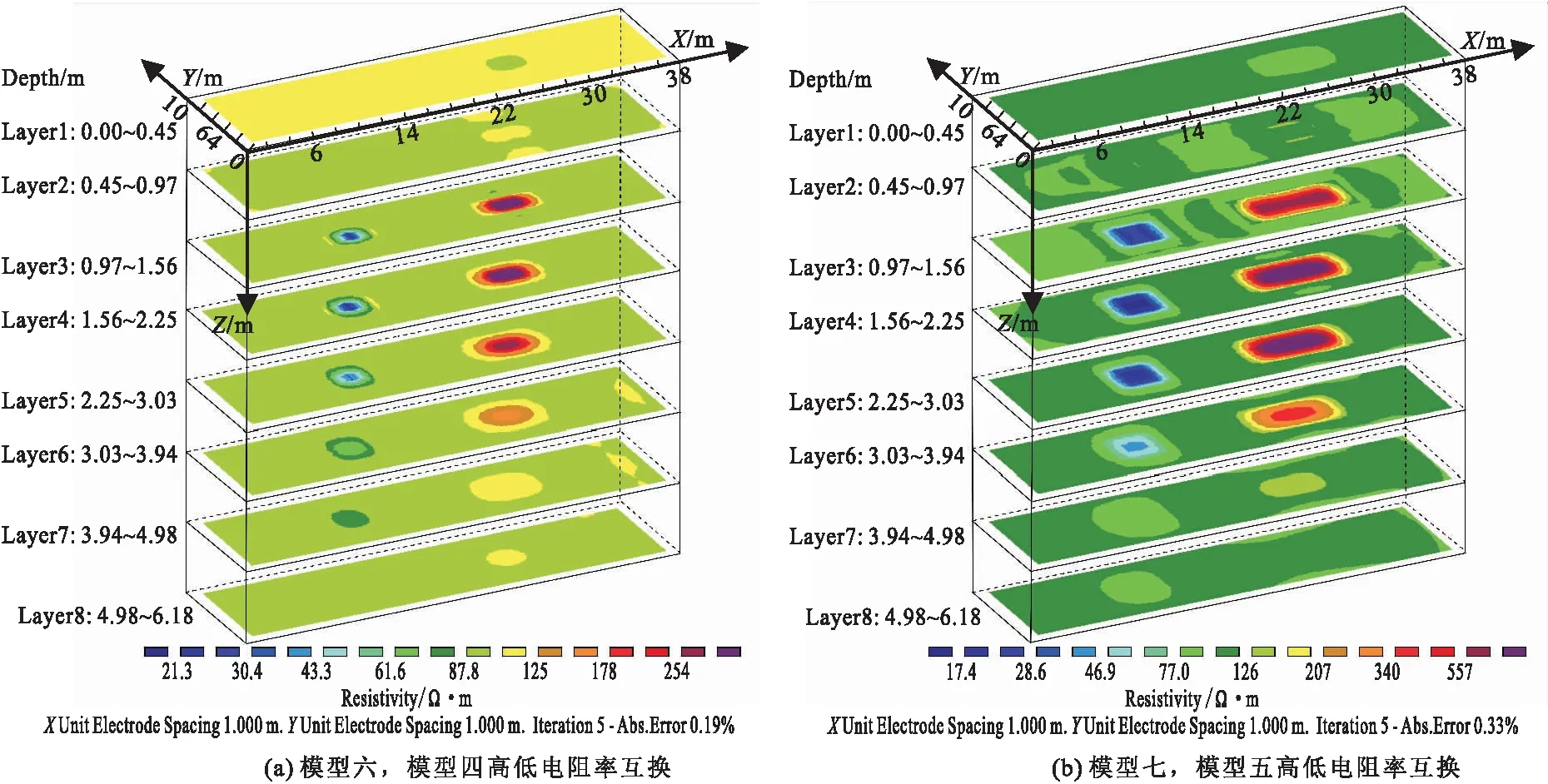
图6 模型六、七高低阻变化反演结果Fig.6 The inversion results of high and low resistance changes in models 6 and 7

模型八和模型九正演模型的Z向切面分别是梯形与偏转45°的正方形，目的在于研究三维高密度电法对于边棱的成像能力(图7)。可以看出，随着深度的变大，边棱逐渐圆滑化。

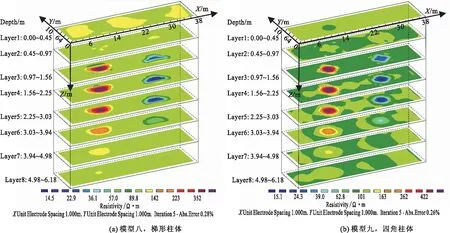
图7 模型八、九边界形状反演结果Fig.7 The boundary shape inversion results of models 8 and 9

模型十和模型十一分别为同一标准上引入凸凹地形因素(图8)。可见地形的起伏变化会对视电阻率分布产生影响，地表凸地形顶点区域呈现出较低阻特征，而在两边小范围内出现较高阻，地表凹地形得到相反的结果，原因在于等电位面在凸处变宽，电流线变稀疏，而等电位面在凹处变窄，电流线变密集。而且地形效应将严重影响局部电阻率分布，使之呈现一定的“起伏状”，体积边界效应也更加明显。

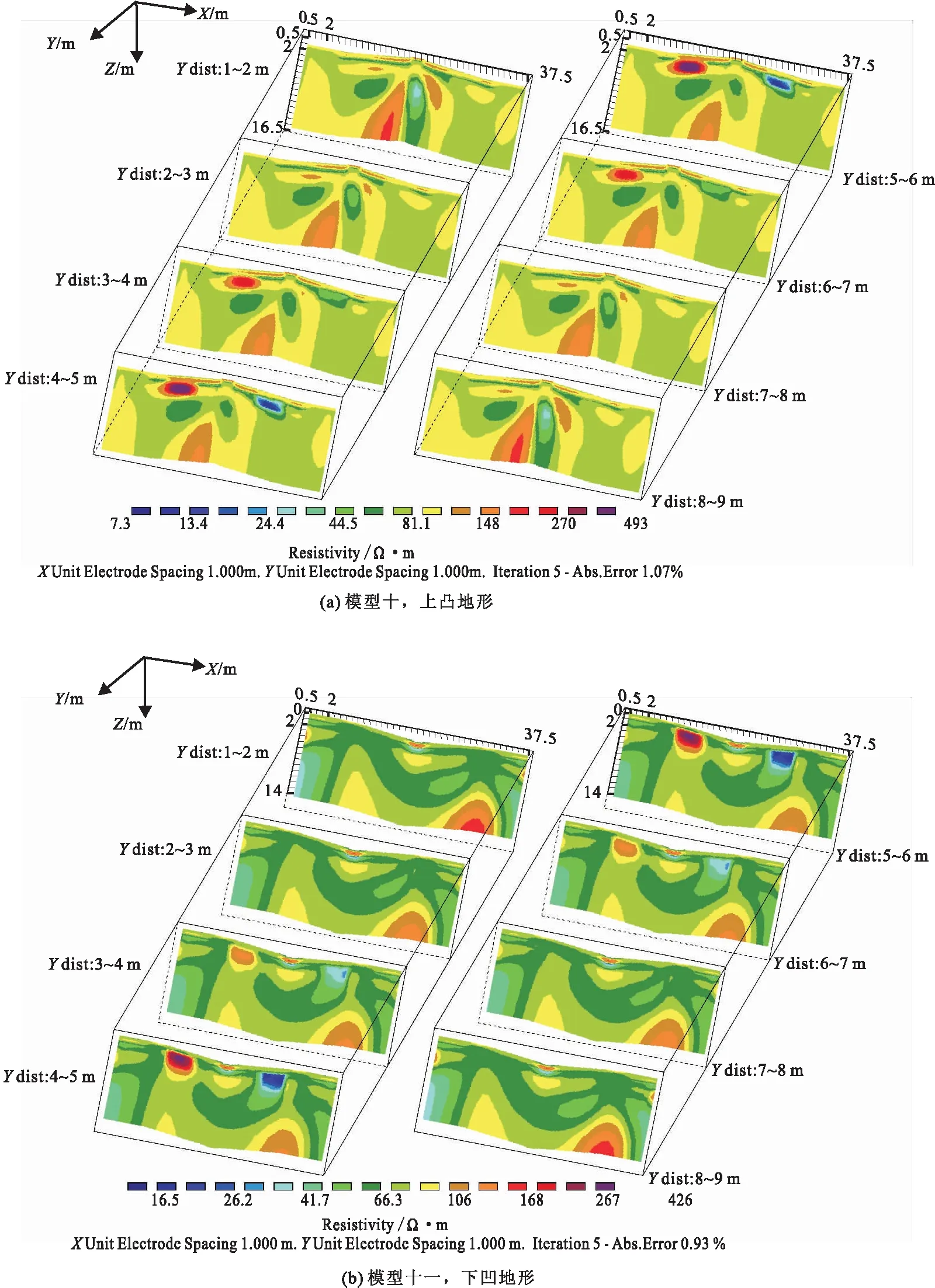
图8 模型十、十一地形凸凹反演结果Fig.8 The terrain convex and concave inversion results of models 10 and 11

此外，模型一反演最小单元体积为0.45个单位，最大为625.694个单位，平均灵敏度为9.603 1，反演结果模型有13层，误差为0.23 %；将模型一X向极距增大一倍，Y向极距不变，同一标准反演结果拟深也增大一倍，最小单元体积为0.9个单位，最大为2 188.685个单位，平均灵敏度为6.956 4，误差为0.7 %，反演模型变为十七层。这说明为了提高勘探深度，可以适当增大测线长度，但若不增加电极，分辨率将会下降。在模型一正演的结果上加入5 %噪声后，反演的误差为3.93 %，这说明了误差并不是越小越好，因为正反演以均质为前提模拟异常，这并不符合实际复杂地质条件，而且在进行迭代计算时，应当依据的是后两次的变化幅度，这符合计算的稳定变化特征。

应用赤道-偶偶极、单极-偶极、偶极-偶极、温纳-施伦贝尔，以及温纳装置对同一模型进行正反演，得到的数据量从大到小为上述装置从左至右。探测深度从大到小分别为单极-偶极、赤道-偶偶极、偶极-偶极、温纳-施伦贝尔和温纳装置。各装置反映的异常体特征相近，但响应的深浅水平位置及边界形状的分辨率有一定差异。

4 实例探测

以大柳塔煤矿52 304工作面附近地裂缝探测为例，本次试验使用E60D高密度电法仪和温纳装置，仅采用了49个电极，电极距为10 m。三维高密度野外工作布线采用图9模式。

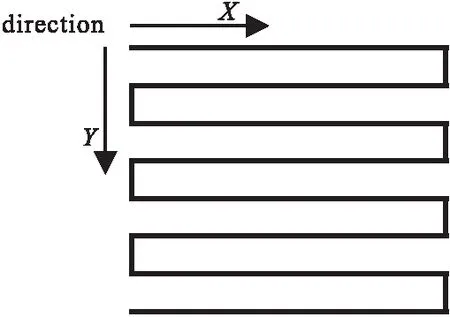
图9 三维测线布设Fig.9 The layout of 3D survey line

由图10可见，探测区地裂缝在地表浅部显现出高阻特性，有一定的布展和延伸趋势，与现场地面状况相符合；此外存在的低阻区域可能与地层赋水情况相关。同时可看到电法固有的体积边界效应，呈现“发散”状态对于异常体位置及范围的圈定是不利的，容易造成“多解性”。

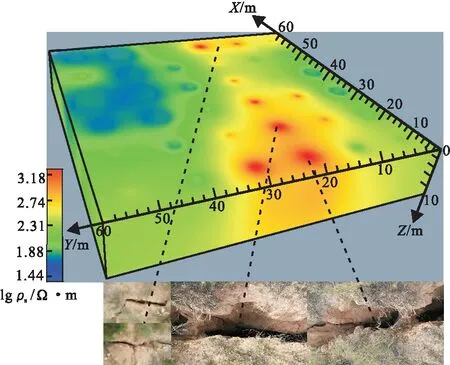
图10 地裂缝反演结果Fig.10 The inversion results of ground fissure

5 结 论

通过三维高密度电法正反演数值模拟，得到了对应异常体的响应规律，注意到高密度电法存在的体积边界效应，受到诸如测线电极距、地质体分布、装置形式、网格剖分，边界条件以及噪声阻尼等参数的叠加影响。因此探测反演结果以平面来看为梯形范围等形式截取可能是比较符合实际的响应范围。在进行高密度电法探测时，需因地制宜选择合适装置，若测线布设长度及电极密度达到要求，三维高密度电法成像后能够以一定分辨率立体展现地质异常体的延展范围与特征，因此该方法在工程与环境地球物理领域是一种有效的探测方法。此外，为避免电法自身存在的缺陷问题以及复杂地质环境的交互影响，多方法综合探测或联合反演是解决三维高密度电法多解不收敛假象的途径。