回焊炉集成电路板焊接炉温曲线数学建模

庄林璐 周克元 毛 靓 董 姝 夏逸飞 王志君

（宿迁学院 文理学院，江苏 宿迁 223800）

对2020 年全国大学生数学建模竞赛A 题“回焊炉焊集成电路板时的炉温最优控制[1]”进行了分析研究，使用最小二乘法拟合出各个位置的比热容参数k，建立约束规划模型求解出所求目标函数的最优值，并画出最优炉温曲线。

1 问题一的模型建立与求解

由热量传导原理分析，建立电路板加热时温度模型[2]：

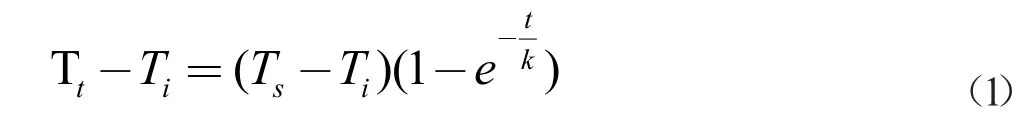
在每个小温区之间的5cm 间隙的温度，根据热量传输原理，间隙温度以左右两端温度为端点成线性函数分布。其中k 为电路板比热容，利用题目所给数据，使用最小二乘法（式（2））求出分段最优k 值（图1）。

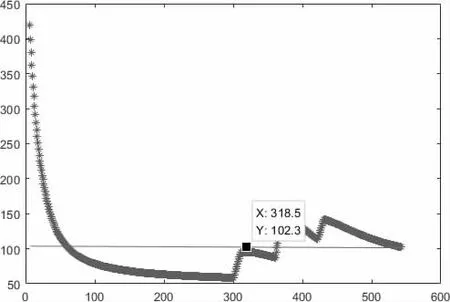
图1 比热容k 曲线图

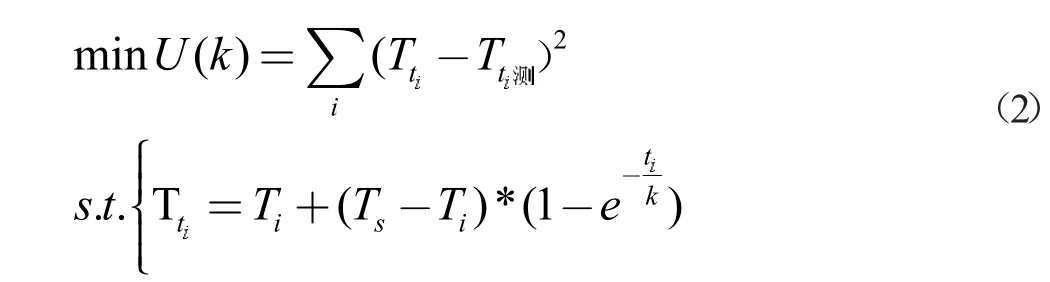
将上述比热容k 及题目数据带入式（1），可计算得回焊炉中各地区的温度，炉温曲线见图2。

图2 问题一数据对应的炉温曲线

2 问题二的模型建立与求解

问题二为求满足制程界限条件的最大传送速度，将制程界限的条件转化为约束条件，传送速度为目标函数，建立约束规划模型，求目标函数的最大值。

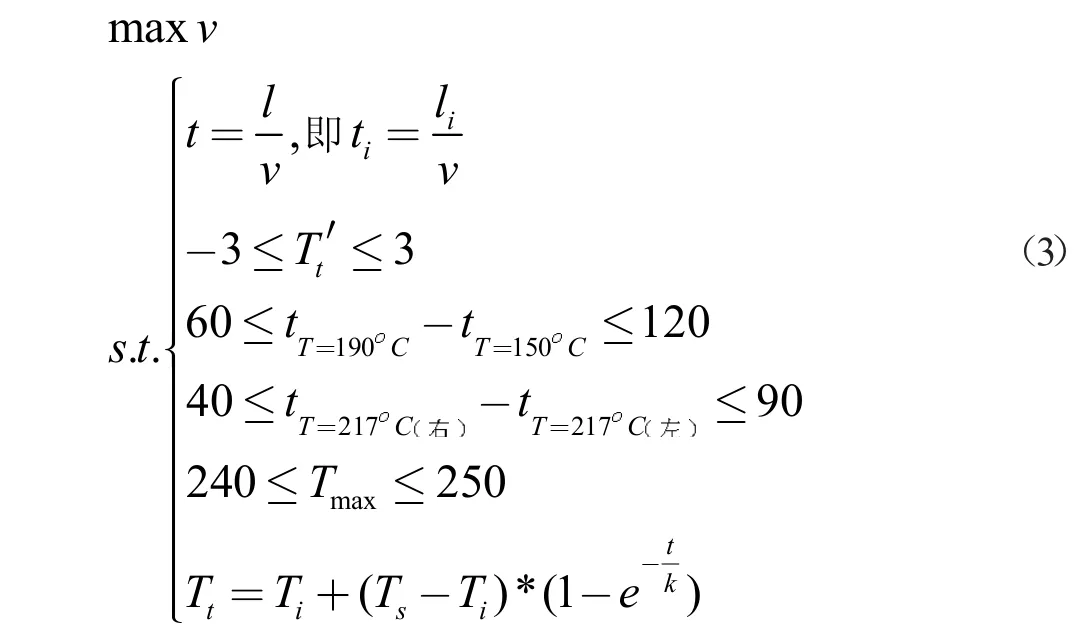
使用matlab 软件[3]在限制范围内对传送速度从大到小按步长进行穷举搜索，求出满足制程界限条件的传送带最大速度为v=70.9cm/min。

3 问题三的模型建立与求解

问题三为求在满足制程界限的条件下，如何设置各温区温度（±10℃温度调节）和传送带传送速度，使得炉温曲线应使超过217℃到峰值温度所覆盖的面积（图2 中阴影部分）最小。

炉温曲线中，超过217℃到峰值温度所覆盖的图形是一个曲边梯形，其面积计算公式为：

积分下限是炉温曲线达到217℃左侧的时间t，积分上限是最大温度（峰值）的时间t。题目中已经指出各温区温度可以进行±10℃的温度调节，所以将每个小温区的温度设为变量，满足±10℃的温度调节范围的限制。

由上分析，建立约束规划模型：

对于模型（5），对传送速度从0 到100、各温区温度在限定范围内，使用matlab 软件按步长进行穷举搜索，搜索出满足限制条件的的最优速度v=70.45cm/min，最优炉温曲线见图3。

图3 回焊炉炉温曲线

4 问题四的模型建立与求解

第四问为在第三问的基础之上，同时还要求以峰值温度为中心线的两侧超过217℃的炉温曲线应尽量对称。即除了需要考虑炉温曲线超过217℃到峰值温度所覆盖的面积最小，还要让以峰值温度为中心线的两侧超过217℃的炉温曲线应尽量对称。

4.1 炉温曲线对称性分析

炉温曲线中，峰值中心线的两侧均有超过217℃的情况，左右两侧可能不完全对称，取两侧同时满足≥217℃的区域进行分析，见图4。

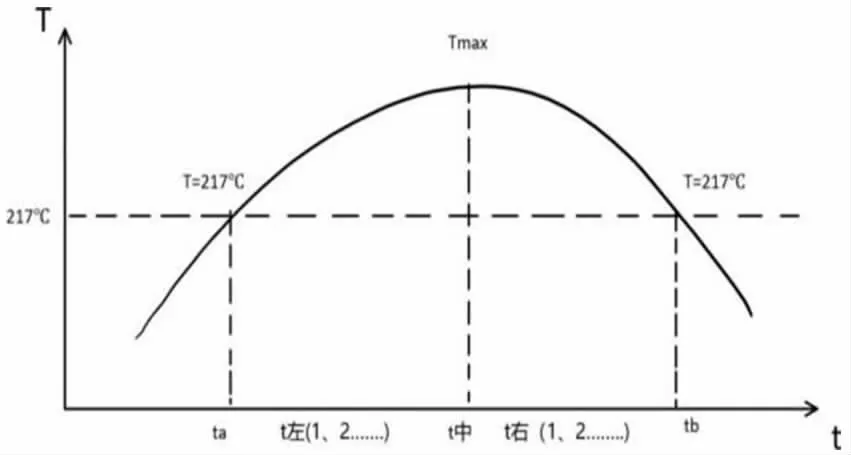
图4 峰值中心两侧温度时间图

取tc=min{t中-ta，tb-t中}，以时间∆t=0.1s 为步长，将时间区间[t中-tc，t中+tc]进行分割为：

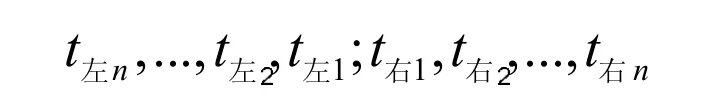
设

将F 作为衡量两侧对称的标准，F 越小越对称。

4.2 模型建立

由上分析，采用双目标约束规划模型进行求解，建立如下双目标规划模型。

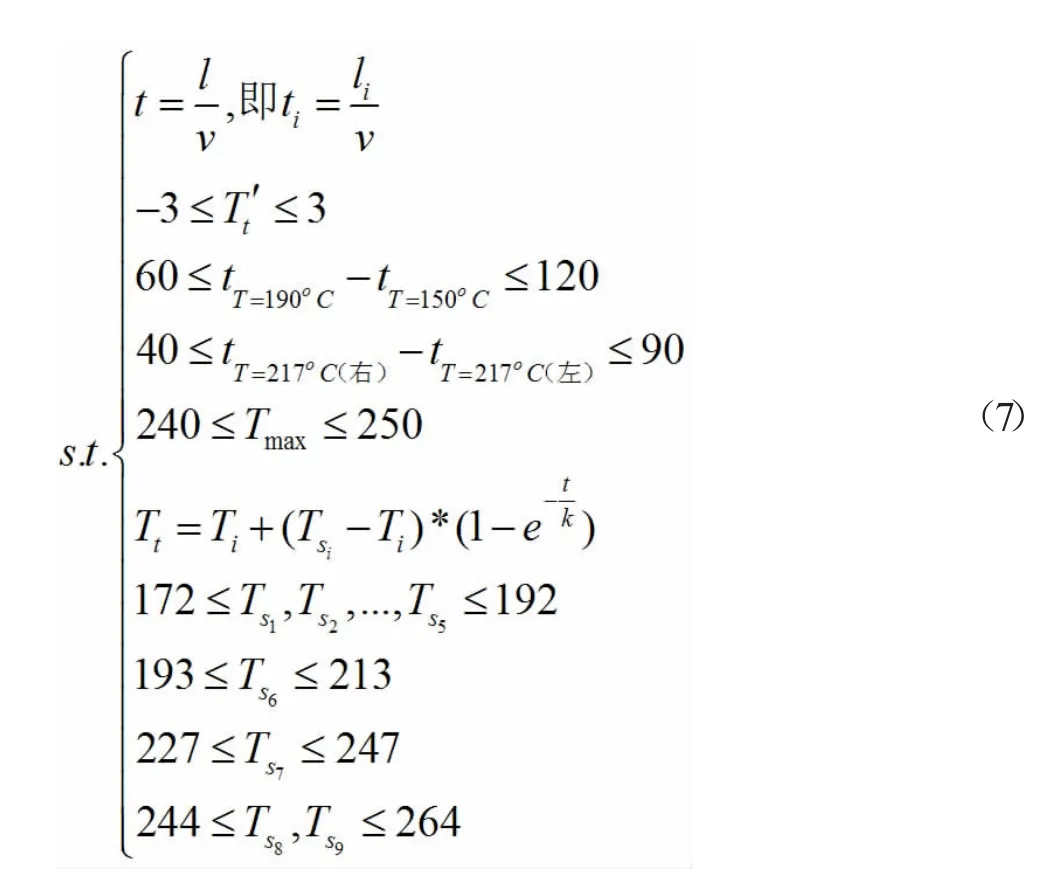
4.3 模型求解

对于上述双目标规划模型，本文采取方法为首先求出单目标函数的最优值，利用该最优值将双目标函数归一化，再加权平均为单目标，将双目标规划模型转化为单目标规划模型求解。[4]对于以炉温曲线超过217℃到峰值温度所覆盖的面积S 为目标函数的约束规划模型，问题三中模型求解出面积最小值Smin=10602.14cm2。再以炉温曲线对称性指标式（6）为目标函数，采取问题三中相似算法，求解出最小值Fmin=6474.63。

求出S 和F 最小值后，对其进行归一化：

分别求S*和F*的最大值。

对于两个目标函数的权重赋值问题，根据题目内容分析和查询相关文献资料[5，6]，主要考虑超过217℃到峰值温度所覆盖的面积最小，次要考虑峰值温度为中心线的两侧超过217℃的炉温曲线应尽量对称。最后，根据不同权重进行计算，不断优化调整权重，使得S、F 与其最小值Smin=10602.14cm2、Fmin=6474.63 偏差都尽可能小，确定出最优权重为63%、37%。

由上分析，建立归一化加权单目标规划模型：

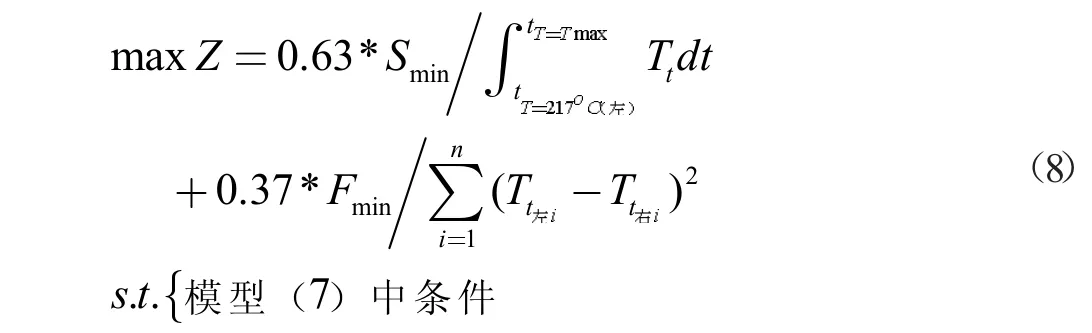
使用相似算法求解，得最优传送带速度v=70.67cm/min，最优炉温曲线见图5。

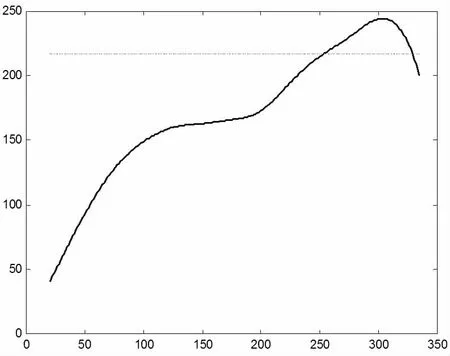
图5 问题四最优炉温曲线

5 模型评价

对于回焊炉焊接的最优炉温曲线问题，综合考虑超过217℃到峰值温度所覆盖的面积最小和峰值温度为中心线的两侧超过217℃的炉温曲线应尽量对称的问题，通过机理分析，建立了双目标约束规划模型，归一化加权为单目标规划模型，编程求解出最优参数，分析严谨，模型合理准确。

本文方法求出的结果也有一些缺点，例如在焊接过程中，电路板的比热容变化无法准确计算；回焊炉设定温度与实际温度可能有误差，焊接过程中的导风也可能会改变焊接温度；同一批次的电路板本身也会有一定的偏差。如上这些情况都可能会影响焊接质量。实际焊接过程中影响焊接质量的因素可能有很多，题目中选取了两个因素，可能不是很全面，后续还需进一步研究，寻找更多的因素指标，建立模型求解更合理的参数数据。