对反铁磁半导体MoCl2 单层的理论预测
2022-02-21唐卉
唐卉
(西南大学物理科学与技术学院,重庆 400715)
自从原子层石墨烯被发现之后[1],二维材料由于其丰富的物理性质和多样的技术应用受到了广泛的关注。设计可能的磁性二维结构是非常有意义的,可以用于自旋电子学和纳米级磁存储设备。纳米级自旋器件不仅可以利用电子的自旋自由度来高密度、高灵敏度地感知、存储、处理和传递信息,还可以克服在目前的半导体技术中,由于器件尺寸的减小而引起的器件结构的散热和能量损失等基本限制。因此,开发纳米级自旋装置对基础科学研究和工业应用都具有重要意义。然而,大多数二维纳米材料,除了极少数例外,没有显示出内在磁性。在非磁性二维材料中诱导磁矩的策略包括缺陷工程、应变、吸附原子和取代掺杂。然而,这样所得到的材料缺乏实验可控性和稳定性。此外,由于强烈的d -d 电子相互作用,金属掺杂剂倾向于形成团簇,导致非均匀磁化和低转变温度。因此,识别磁性二维纳米材料一直是一个重大的挑战。
二维铁磁性材料在自旋电子器件中有着广泛的应用,但不可忽视的是,自旋电子学也是研究反铁磁材料的重要方法。与铁磁自旋电子学不同,反铁磁自旋电子学的工作原理是利用隧道各向异性磁阻效应(TAMR),该效应对外界磁场不敏感。随着器件尺寸的不断减小,磁阻信号得以保留。近年来,二元过渡金属二卤化物MX2(M=过渡金属,X=卤素:Cl,Br, Ⅰ)因其诸多优点而受到越来越多的关注。它们形成由一维链或二维层组成的低维晶体结构。因此,这一系列材料为研究低维磁性提供了丰富的空间。关于单分子层,在过去一段时间里人们已经做了一些理论的努力。在本文中,我们基于密度泛函的第一性原理研究系统地计算了MoCl2的性质。正如在石墨烯和MoCl2中报道的,材料中较大的层间分离提供了将其剥离为单层的可能性。与此同时,计算表明MoCl2单层是间接带隙约为1.64eV 的反铁磁半导体。在密度泛函理论(DFT)计算,我们研究了MoCl2单层的几何结构、稳定性、电子和磁性能。
1 研究方法
所有计算均采用密度泛函理论的投影- 增广波(PAW)方法,该方法由维也纳从头算模拟软件包(VASP)实现[2]。交换相关函数是具有广义梯度近似的PerdewBurke-Ernzerh(PBE)泛函[3]。Mo 原子和Cl 原子的核外价电子分别为4d55s1和3s23p5。为了说明部分填充的Mo 原子d 轨道之间的强相关性,采用自旋相关的GGA+ Hubbard 修正U (GGA+U)方法[4]来考虑场电子的相关性。因此,Mo 原子的有效库仑交换参数(Ueff=U-J,其中U 为库仑相互作用,J 为交换能量参数)设为3ev。为了避免相邻单分子层之间的相互作用,在二维单分子层中沿z 方向插入真空(约17Å)进行建模。采用阈值为500 eV 的平面波基以及5×5×5 和5×5×1 的K 点网格(Monkhorst-Pack k-point)分别对MoCl2块体和单分子层在布里渊区积分。在模拟过程中,所有原子的晶格常数和位置都进行松弛处理,直到赫尔曼- 费曼力小于0.01eVÅ-1,总能量的收敛判据设为1×10-5eV。此外,计算了能带结构和总电子态密度(DOS)且采用密度泛函微扰理论[5]对MoCl2单层的原胞进行声子色散计算。
2 结果讨论
我们首先采用PBE+U 方法优化了MoCl2块体的几何结构,沿块体的001 面设计了二维MoCl2单分子层的初始结构。与MoS2类似,大部分的过渡金属二卤化物具有如图1(a)所示的自然层状结构,层间的范德瓦尔斯(VdW)间隙显著。对于块体结构,计算时采用了一个2×2×2 的超胞,通过自旋极化计算对铁磁(FM)、反铁磁(AFM)两种磁构型进行结构优化,MoCl2块体经过优化后的晶格常数为a=b=3.555Å,c=5.916Å。
MoCl2单层如图1(b)所示,它由三个原子平面组成:一层Mo 原子夹在两层Cl 原子之间。对于单分子层,采用2×2×1超胞, 结构优化后的晶格常数为a=b=3.664Å,c=19.292Å。我们考虑了铁磁(FM)、反铁磁(AFM)和无磁(NM)三种不同类型的磁配置, 进行自旋极化计算。计算所得的能量如表1 所示。可以看出,MoCl2是反铁磁性的。
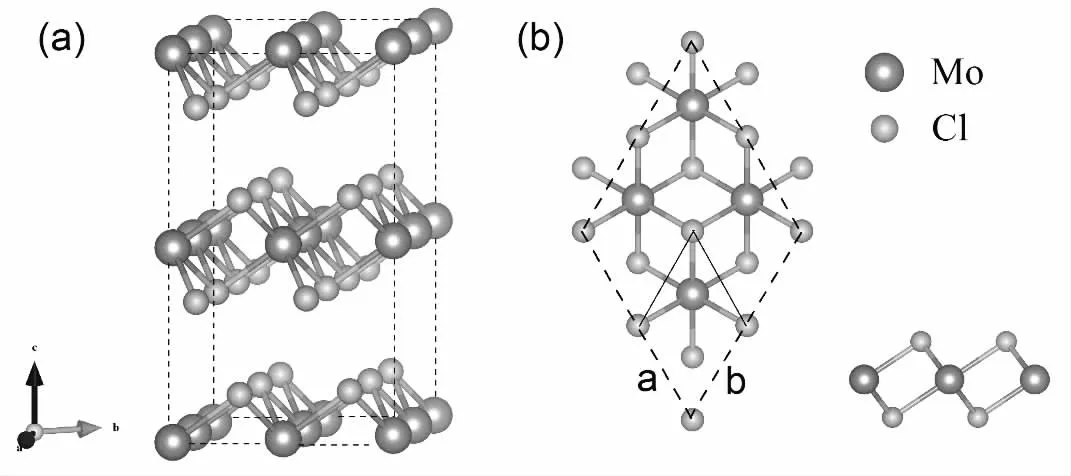
图1 MoCl2 优化后的几何结构(a)块体、(b)单层

表1 MoCl2 块体和单层的不同磁构型的能量及单层的弹性常数
材料结构的稳定性对其实际应用至关重要。接着我们对稳定性(包括动态稳定性和机械稳定性)进行了评估。动态稳定性可以通过使用密度泛函微扰理论计算材料的声子色散来确定。频率的正值表明晶体是动态稳定的,而负的频率表明系统在晶格动力学上是不稳定的。如图2 所示,在布里渊区内,MoCl2单分子层的所有振动模均为正频率,表明MoCl2单分子层是动态稳定的。低频率(小于5THz)的振动模式由三个声学分支组成。原子质量较大的Mo 原子主要致力于较低频率的声振动模式,而高频光学分支主要由原子质量较小的Cl 原子贡献。
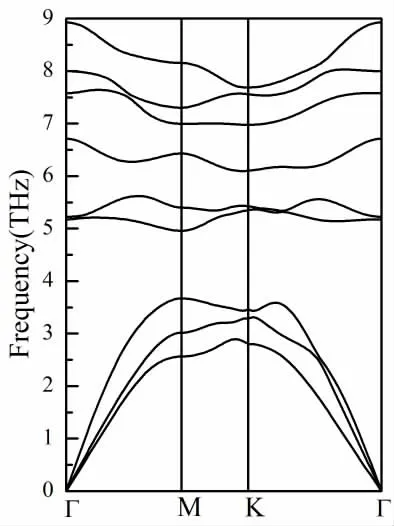
图2 Mocl2 单分子层的声子色散曲线
进一步计算了弹性常数,验证其机械稳定性。机械稳定性描述了在应变条件下对抗变形或畸变的稳定性。对于二维晶体,可根据胡克定律给出弹性常数与模的关系。晶格的弹性行为可用其二阶弹性常数矩阵来描述[6]。
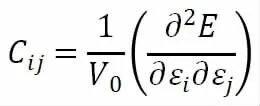
式中,E 为晶体的能量,V0为晶体的平衡体积,ε 为应力。独立弹性常数的数量取决于二维晶体的对称性。六方晶体具有两个独立的弹性常数,弹性稳定性的充分必要条件C11>0 和C11>|C12|。由表1 可知,单层MoCl2的弹性常数满足弹性稳定标准,即单层MoCl2在施加一定范围的机械应变后是稳定的。
计算了MoCl2单层的能带结构和态密度。如图3 所示,单层表现出一种反铁磁半导体性质,计算得到的间接带隙为1.64eV。Bader 电荷分析表明,在MoCl2单层中,每个Mo 原子有电子转移到相邻的Cl 原子,每个Cl 原子从相邻的Mo 原子获得电子。Cl 原子具有较强的亲和力,能够获得额外的电子来填充其外层,Cl 原子的电负性比Mo 原子大,从而使电荷转移方向合理化。我们进一步考虑自旋轨道耦合效应,考虑了平面内(x, y 方向)和平面外(z 方向)的磁矩方向。计算表明MoCl2单层具有一个沿z 方向的易磁轴。计算MoCl2单层的 磁 各 向 异 性 能(MAE) 为Ez-Ey=2.575meV、Ez-Ex=5.444meV。该结果比纯金属(如Fe (1.4 eV / Fe 原子)、Co (65 eV / Co 原子)和Ni (2.4 eV / Ni 原子)[7]的磁各向异性能大一个数量级。如此大的磁各向异性能使得MoCl2单层在反铁磁自旋电子学中具有广阔的应用前景。

图3 MoCl2 单层的能带结构和态密度
低维材料通常对外界刺激表现出敏感的反应,这使得其在各种条件下的电子和磁性能具有可调性和富集性。为了研究MoCl2单分子层在自旋电子学中的可能应用,讨论了平面双轴应变对其电子和磁性的影响。应变的定义为ε(%)=(a-a0)/a0×100%,其中a0和a 分别表示无应变和应变对应的MoCl2单层的晶格常数。ε 的正值表示拉伸,而ε 的负值表示压缩。ε 的数值范围从-2%到2%。施加的应力可能影响MoCl2单分子层的基态。因此,如图4 所示,MoCl2单层的总能量随着压缩或拉伸应变的增加而增加,表明在变形过程中MoCl2单层没有发生破坏。反铁磁与铁磁间的能量差总是正的,说明对于不同的形变结构,反铁磁态总是比铁磁态更加稳定。在-2%~2%的应力范围内,单个Mo 原子的局部有效磁矩几乎呈线性变化,磁矩从1.764μB增加到1.810μB。此外,我们还讨论了其带隙在不同应力下的变化,带隙的变化范围约为0.16 eV,MoCl2的能带对外加应力不敏感,证实了MoCl2单层在外力作用下反铁磁半导体性质的稳定性。
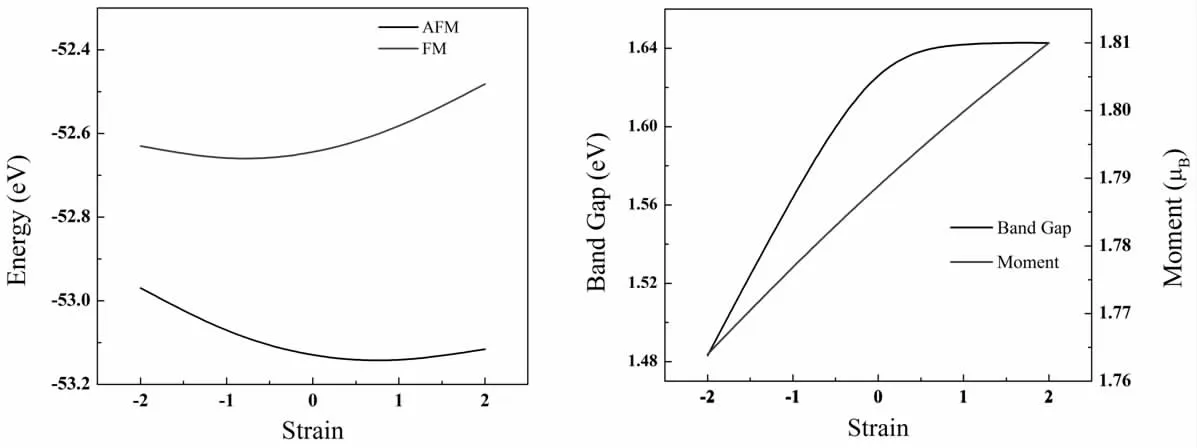
图4 能量、带隙以及单个Mo 原子磁矩随应力的变化
3 结论
我们使用DFT 与GGA+U 方法研究了层状MoCl2单层的几何、稳定性、电子和磁性质。MoCl2呈三原子层结构,中心层由Mo 原子构成,顶层和底层由Cl 原子构成。MoCl2单层的自旋极化态密度和能带结构计算表明,MoCl2单层是间接带隙约为1.64eV 的反铁磁半导体。声子色散和弹性模量计算表明,MoCl2单层在动力学稳定和机械稳定的。此外,外加双轴应变可以显著地调节能量,带隙和单个Mo 原子的磁矩,但反铁磁半导体性质对外加应变是稳定的。这些结果为MoCl2单分子层在反铁磁自旋电子学器件中的应用提供了可能。
