基于拓扑链路识别的光网络流量数据合成算法
2022-02-21吴树霖张江龙吴小华庄浩涛赵永利
周 刚,吴树霖,张江龙,吴小华,庄浩涛,赵永利
(1.国网福建省电力有限公司,福州 350003; 2.国网福建省电力有限公司信息通信分公司,福州 350003;3.安徽继远软件有限公司,合肥 230088; 4.北京邮电大学,北京 100876)
0 引 言
在投入商业使用的光网络中,用户隐私和商业机密保护等措施使得实时采集到的有效流量有限,难以支撑基于深度学习的流量预测或流量诊断等模型的训练。
数据增强(合成)是解决数据量问题的有效方法。传统方法依据已知流量数据特征和专家经验,对经典数学模型进行再建模,以拟合出流量分布表达式。文献[1]根据泊松模型对流量数据进行数学建模,但现网中业务种类繁多,流量数据特性越加复杂,基于泊松模型的数据合成会导致多源数据汇聚后变得越加失真;文献[2-3]中均基于分形布朗运动模型对流量数据进行数学建模以合成流量数据,该模型能够刻画光网络的突发性和自相似性[4],但不适用于非高斯流量数据的建模。可见传统方法根据局部特性合成流量,难以适应现网高度变化的流量数据。为了解决生成对抗网络(Generative Adversarial Networks,GANs)[5]难以合成序列数据的问题,文献[6-7]基于循环神经网络(Recurrent Neural Network,RNN)提出了针对序列数据的合成方法;为了解决时序数据条件性合成问题,文献[8]引入基于多层感知机的元数据辅助模型。然而尚未有根据光链路特性对流量数据进行合成的研究成果。
针对上述流量合成方案的局限性,本文采用GANs的“半监督”能力代替专家经验,构建了基于拓扑链路识别的光网络流量数据合成(Topology-link Recognition-based Optical Networks Traffic Data Synthesis, TRONTDS)模型 。
1 拓扑模型与问题描述
1.1 拓扑模型
在进行流量数据增强算法的研究之前,先设定算法网络模型。图1所示为图像化的光传送网(Optical Transport Network, OTN)拓扑图,给定的OTN由1组OTN节点和1组OTN链路组成,可用无向图G=(V,E)来表示该物理拓扑, 式中,V为物理节点的集合,E为光纤链路的集合。设Pp为所有物理路径的集合,pp(src,dst)∈Pp为从源节点src∈V到目的节点dst∈V的物理链路。对src和dst间的链路pp(src,dst)进行数据增强,则将pp(src,dst)链路和端节点进行异化。本文采用颜色变换法对指定链路进行异化,使得数据增强模型能够识别出该链路。
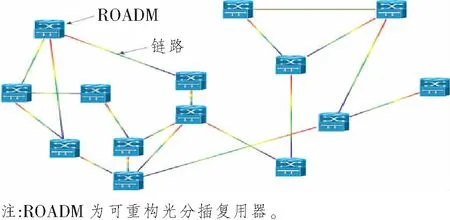
图1 图像化的OTN拓扑图
1.2 核心问题描述
结合以上拓扑模型,给出几组定义和概念:
(1)vi为对光网络中链路i进行测量得到的流量数值。
(2) 将链路i中一段经过预处理后包含n个流量的测量序列定义为
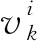
(3)DSt,i为链路i中t维光网络流量序列集,有以下关系:

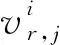

(5) 高斯白噪声Zn到Sn,i的映射过程为


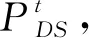
2 基于拓扑链路识别的光网络流量数据合成算法
2.1 GANs基本理论
GANs包含了两个重要结构——DM和GM[5]。GANs核心思想为GM与DM基于双元零和博弈策略进行对抗学习——GM与DM在对抗学习中争取各自“利益”的最优化,且双元博弈“利益”总和为一个设定的常量。GM的输入为随机向量,一般为低维数据,如高斯白噪声。GM的任务就是通过学习到的经验(初始随机设定)将该低维随机向量进行处理后,根据输出规定映射成一个多维或者高维数据。不同于GM,DM基于真实数据集,因此其初始输入为真实的数据集,在对抗学习中输入的是GM生成的数据。在GANs训练过程中,DM的任务是对输入数据进行真实性的鉴别并将鉴别结果作为输出。GM目标是合成具有高度真实性的数据以使得DM无法鉴别出该数据为合成,同理可知,DM的目标是在对抗学习中不断积累新“知识”,最大程度判别出GM合成的数据为非真实数据。从数学建模角度分析,GM的目标是对联合概率分布P(X,Y)进行学习,X为数据特征,Y为标签,从而GM可以根据该先验分布进而获悉后验分布P(Y|X)=P(X,Y)/P(X)。DM的目标是基于原始数据集直接学习P(Y|X)分布,并根据数据特征算出标签的概率。图2所示为GANs模型的基本结构。

图2 GANs模型的基本结构
正是由于DM与GM的目标是相反的,因此GANs的训练过程呈现出双元对抗性。GANs在数据生成中的整体任务是通过学习获得数据特征知识,进而依据学到的知识生成符合原始数据分布规律的能够以假乱真的合成数据。在这个训练过程中,GM在DM模型的“反馈”下学习到真实数据的具体分布规律,并不断生成新的数据输出给DM进行判别,在不断迭代的过程中,GM生成数据能够完全逼近实际数据,DM需要根据先验知识对GM所生成的数据进行鉴别,在每次迭代过程中导出鉴别的真伪结果。对于GANs的整体训练过程而言,博弈双方DM与GM的最终目标是趋向于动态的纳什均衡。在GANs趋向于博弈均衡时,GM能够生成逼近真实数据分布的合成数据,且DM所导出的判别结果趋近于0.5。
GANs的目标函数为
式中:G为GM的输出;D为DM的输出;Pz(x)为噪声分布;E为期望;log对数的底大于1,一般取2或e;Pdata(x)为真实数据集的分布规律;G(x)为GM处理输入数据的过程(如将随机高斯白噪声向量z转换成目标多维数据);D(x)为数据x服从真实数据集分布规律Pdata(x)而非合成数据集分布规律Pg的概率。
2.2 拓扑链路识别与相应流量数据合成算法
图3所示为基于拓扑链路识别的光网络流量数据合成算法框架图。

图3 基于拓扑链路识别的光网络流量数据合成算法框架图
不同于传统的GANs,其在GM中引进CNN[9]以合成“伪”拓扑向量。相应地,需要在DM中引入一个辅助模块(同样为一个CNN)用于鉴定“伪”拓扑向量并反馈信息给拓扑GM。由于流量数据为离散形式的序列数据且含有时间维度的特征,引入一种具有高效学习数据时间特性的神经网络——RNN[10],用于合成流量数据。相较于原始的RNN,改良的长短时记忆(Long Short Term Memory,LSTM)[11]神经网络能够获取到数据中较长的时序依赖关系,被广泛应用于处理具有时间维度的离散数据,本文采用LSTM作为GM的核心部分。根据条件生成网络[12]的思路,结合生成的拓扑向量与生成的流量数据作为核心DM的输入。通过DM的反馈,GM能够逐渐合成接近真实流量数据的合成流量,同时获取到拓扑向量和流量数据之间的关系。
基于原始GANs模型的目标优化函数进行的模型训练,在稳定性保持方面能力较差,也容易发生模式崩坏问题。研究结果表明,Wasserstein距离用于改善目标函数,能够降低模式崩坏问题发生概率[13]。本章提出的缺失值填充算法采用了“W距离”GANs,用于学习缺失时序数据的分布。如式(8)所示,相较于原始版本的GANs,Wasserstein距离的引入主要体现在目标函数以下两项的修改中:
(1) 将目标函数中的对数函数省去了;
(2) 在GM和DM每次迭代更新的过程中,对模型相关参数进行取模并做出裁剪处理,以达到让其保持在一定的范围之中。
式中:WL(G,D)为目标函数;PDSt为原始样本数据集的数学分布;s为DM的输入,而DM的构建需要喂入原始数据序列,所以此处的s为原始数据序列D(s),表示喂入s序列的DM的输出;Z为噪声分布,PZ为生成模型生成的伪数据分数学分布。
由此DM中引入了辅助DM,如图3所示,那么需要对基于Wasserstein距离的目标优化函数进行调整,也即引入辅助DM数学模型。基于式(8),TRONTDS的目标优化函数设计如下:

3 仿真设置及结果分析
3.1 指标设定
为了对增强后的光网络流量数据的质量进行评估,本文采用了两个层面的指标,分别是从数据本身出发的数学统计指标(自相关系数)和基于数据构建的神经网络模型的准确率应用层面的指标。
(1) 自相关系数(Auto-correlation)
自相关系数用于衡量同一个序列在两个不同时期的相关程度,也即历史数值对当前数值的影响。从计算的角度看,自相关系数就是将一个数据列在时间维度上按照一定时间进行平移,去除平移后时间重叠的两列数据,最后对这两列数据进行相关系数求解。
自相关系数的计算式子如下所示:

自相关系数可用于衡量流量数据在时间前后的相关性,进而对数据增强模型在时间特性方面的捕获能力进行评估[14]。
(2) 预测准确率(Accuracy)
准确率指在给定测试数据集的情况下,神经网络模型进行数据分析和判断,最终输出结果为对应样本种类的次数与总样本数之比。本文设定光网络流量预测值的合理偏差范围为真实流量值的30%,也即预测值与真实值的绝对差值与真实值的百分比小于30%判定预测结果为真,否则为假。
3.2 仿真设置
为了验证TRONTDS在数据增强方面的性能,减弱CNN模型训练过程对整个算法流程的影响,本文设置9节点、12链路的网络拓扑作为仿真拓扑,如图4所示。设定该拓扑中节点序号由左到右、由上到下递增。流量数据采集粒度设定为1 h,跨度为24~48 h,整理出变长流量序列,组合成数据集。流量数据集分为训练集和测试集,比例设定为4∶1。

图4 9节点、12链路拓扑图
在统计指标层面,本文采用真实数据和原始GANs合成局作为基准对比。由于原始GANs不具备拓扑识别能力,故本文仅针对指定链路pp(node2, node5)(node2, node5分别为图4中第2个和第5个节点)流量进行仿真对比。在应用指标层面采用原始GANs和LSTM神经网络作为对比基准。
本文核心DM采用包含4个中间隐藏层的多层感知机(全连接神经网络)来实现,每个隐藏层的神经元个数设定为200;辅助DM选用CNN,选用ReLU函数作为激活函数,池化层包含3个卷积层和1个全连接层。对应的流量数据GM采用一层LSTM网络实现,包含100个单元;拓扑向量GM也采用3卷积层的CNN。添加Softmax层用于输出指定链路pp(node2, node5)的合成拓扑向量和合成流量数据。训练过程中梯度惩罚权重设定为10,采用Adam optimizer作为优化器,学习率为0.001,损失函数为Wasserstein函数。
3.3 结果验证与分析
本文对指定链路pp(node2, node5)进行流量数据合成,与真实数据的对比如图5所示。可见两列流量数据的走势以及波动趋势基本保持一致,生成的流量数据基本拟同真实数据。图6所示为真实流量数据和生成流量数据的频次分布直方图,通过比较可知,合成的流量数据分布与真实数据分布基本上能够匹配,其中橘黄色曲线为本文增强后流量频次高于真实流量的部分。

图5 指定拓扑链路增强流量数据与真实流量数据对比图

图6 指定拓扑链路增强流量数据与真实流量数据直方分布图对比
为验证TRONTDS合成数据具有真实流量数据的时间特性,对本文合成流量数据、原始GANs合成数据和原始的流量数据分别进行自相关系数计算,结果如图7所示。由图可见,TRONTDS合成的数据从低滞后时间到高滞后时间,几乎与原始流量数据变化重叠,这说明TRONTDS能够高效获取原始流量数据的时间特效,而原始GANs合成数据的自相关系数曲线出现许多抖动且波峰出现更多失真,这说明其容易丢失流量数据中所携带的时间特征。
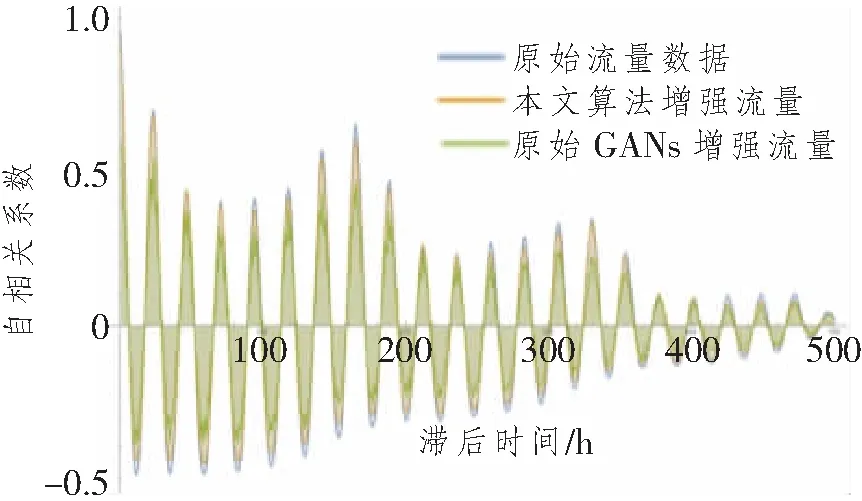
图7 原始流量数据与两种算法合成数据自相关系数对比图
图8所示为基于3种增强数据训练的全连接神经网络的流量预测准确率曲线,其中基于TRONTDS合成流量的预测模型性能最佳,能够快速将准确率提升到90%以上,这主要是由于TRONTDS在GANs基础上引入了LSTM网络,能在半监督机制下生成与真实流量数据相同数学分布的流量数据。同时可见,模型能够关联拓扑向量GM合成的拓扑向量和合成的流量数据,使得能够指定链路进行流量数据的合成。

图8 基于3种增强算法合成数据的流量预测模型准确率对比图
4 结束语
为了能够对光网络指定链路中的流量数据进行增强,本文提出了一种TRONTDS算法,在GANs框架下联合基于光网络拓扑的条件生成模型和基于光网络流量的数据合成模型,以自监督的方式合成指定光链路的流量数据。仿真结果表明,所提算法在统计指标和应用指标上均表现优异,其中合成的光网络流量数据在自相关系数指标上与真实数据接近,且使得基于全连接神经网络的流量预测模型准确率达到95%以上。为了验证合成流量的质量,本文目前只对9节点拓扑进行了仿真,以减小拓扑识别效率对整体算法的影响。后续工作将着重优化拓扑识别功能,并在现网拓扑上采用真实流量数据进行仿真验证。
