基于多维数据管控的人力资源系统决策研究
2022-02-21付振罡崔晟豪姜冬赵阳马鑫
付振罡, 崔晟豪, 姜冬, 赵阳, 马鑫
(1.国家电网有限公司,客户服务中心,天津 300309;2.北京中电普华信息技术有限公司,北京 100085)
0 引言
推进人力资源的系统化建设,需要构建优化的人力资源系统多维分析与决策支持模型,实现对人力资源系统的人员调配、员工培训、整体运营。应用决策支持技术构建人力资源系统,加快人力资源管理从单纯的职能管理向信息化管理转变,实现人力资源系统优化配置。目前,我国人力资源信息监控和预警存在着模式粗放、方式单一和效率低下的弊端,如何实现人力资源管理精细化、科学化和规范化,成为人力资源系统亟待解决的问题。人力资源系统决策是建立在对人力资源信息的融合和优化决策基础上,结合模糊信息融合技术,进行人力资源系统决策的信息融合设计。构建人力资源系统人员调度和管理的多维分析与决策模型,结合模糊支持学习方法,进行人力资源系统的调度,采用模糊信息融合技术,进行人力资源系统决策的优化设计,提高人力资源系统的优化管理和决策能力[1],相关的人力资源系统决策研究受到人们的极大关注。但是传统方法的人力资源系统决策的准确率较低,抗干扰性较差。
针对传统方法存在的问题,本文提出基于多维数据管控的人力资源系统决策方法。首先采用信息采样技术挖掘人力资源系统决策的多维数据,并利用纳什均衡解的方法,将多维数据管控步骤转换为多维解向量优化问题,提取多维数据管控特征,然后基于多维数据管控方法,完成人力资源系统决策模型的构建,最后进行仿真测试分析,展示了本文方法在提高人力资源系统决策能力方面的优越性能。
1 人力资源系统决策的多维数据分析
1.1 人力资源系统决策多维数据挖掘
为了实现基于大数据平台的人力资源系统决策多维数据智能调度,对公司人力资源系统库中的离职人员的历史数据进行挖掘分析,希望可以从中发现其主要特征,避免由于人才流失所造成的公司相关重要岗位的缺失[2-3]。采用量化寻优方法获取人力资源系统决策的最优解,结合特征空间重构方法,更新人力资源系统决策数据,利用信息采样技术进行多维数据挖掘[4-6],通过权重分析,构建人力资源系统决策的非合作博弈模型,采用纳什均衡解的方法,将多维数据管控步骤转换为多维解向量优化问题,提取人力资源系统多维数据管控的优化特征,从而提高人力资源系统决策和管控能力。首先构建人力资源系统决策的模糊识别函数如式(1),
(1)
式中,omi和rmi分别表示i维上的投影和形状特征,其形状用0与1组成的长度为n个比特的二进制数进行描述;d表示特征子集的范围。采用量化寻优方法,进行人力资源系统决策的规则集更新[7-8],得到隶属度函数式(2)、式(3),
p=a×Pbest(i)+(1-a)×Gbest
(2)
X(i)=1±a×|Pbest-Dp(om,rm)|×ln(1/u)
(3)
其中,a,u为0到1之间的随机数,Pbest为人力资源系统决策的最优解,即个体极值。

(4)
式中,t表示人力资源系统决策。采用目标排序的方法,进行人力资源系统决策的线性规划设计[9],得到优化的规划函数,利用信息采样技术,进行人力资源系统决策的多维数据挖掘,其表达式如下:
(5)
根据大数据挖掘结果,进行人力资源系统决策和样本筛选,提高信息融合聚类和特征提取能力[10]。
1.2 多维数据管控的优化特征提取
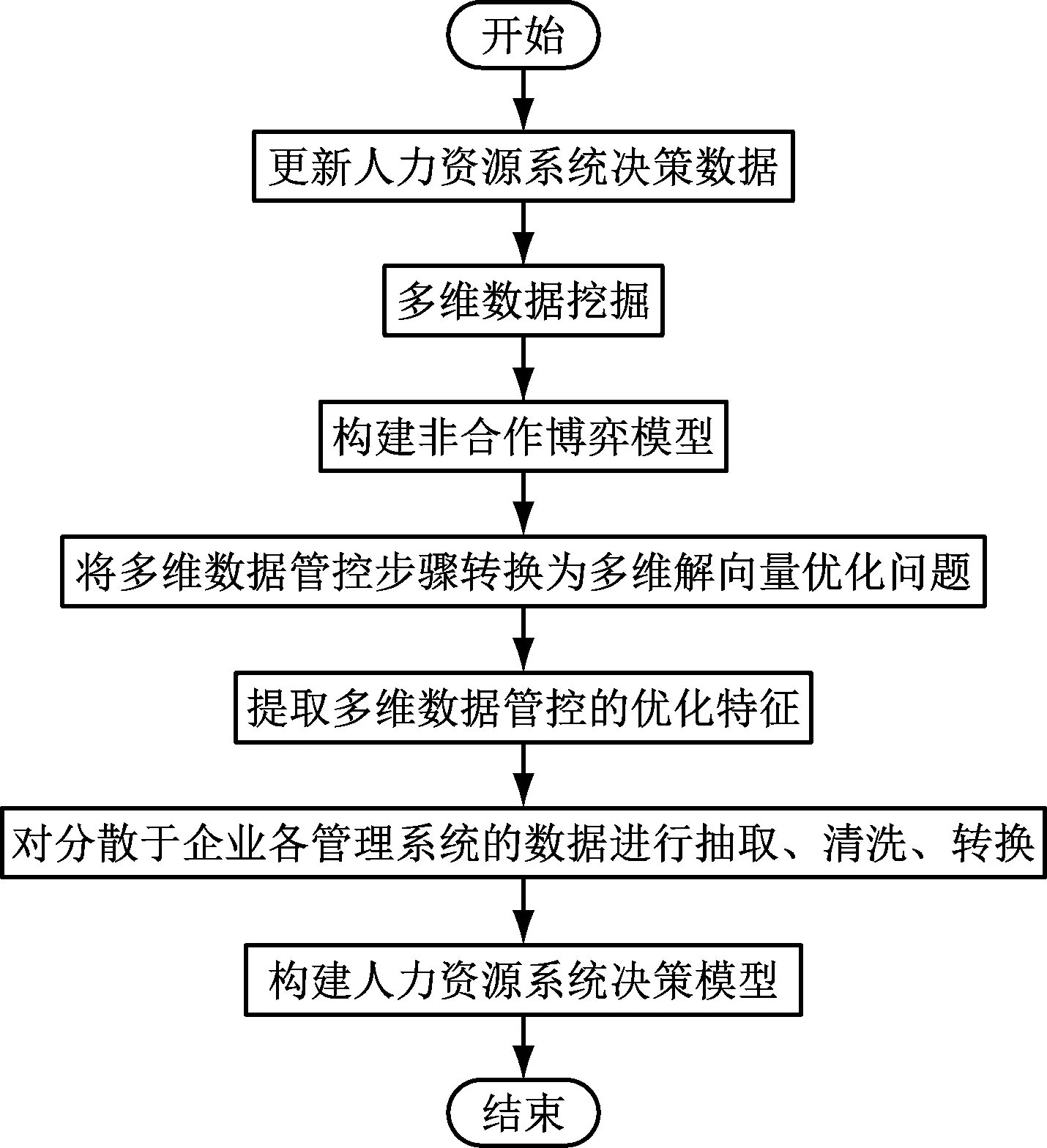
在上述人力资源系统决策多维数据挖掘的基础上,采用定量递归分析方法进行人力资源系统决策过程中的多维数据融合,得到多维数据管控样本信息为Xi,观测器模块的特征分布函数为Nf,若(Nf/N)<δ,表示人力资源系统决策的中心位置向量集,若Yc (6) 根据人力资源系统信息融合度函数进行权重分析,得到人力资源系统决策的非合作博弈模型如式(7)。 (7) (8) 根据特征提取结果,进行局部寻优,提高人力资源系统决策和管控能力,提升人力资源系统决策调度的吞吐性能[13-15]。 根据提取的人力资源系统多维数据管控的优化特征,结合多维数据管控方法,利用联机分析处理工具,以报表的形式构建人力资源系统决策模型。采用交叉编译方法,评价人力资源系统决策的最优局部概率。将α(i,j)表示人力资源系统决策节点在(i,j)状态时的发送状态,则人力资源系统决策的竞争模型如式(9), (9) (10) (11) 根据上述分析,构建人力资源系统多维决策的模糊信息分量,对分散于企业各管理系统的数据进行抽取、清洗、转换后加载到数据仓库,得到更新规则如下: (12) (13) Xj(t+1)=pj(t+1)±β× (14) 式中,Xj(t)为第t代人力资源系统决策的规则函数。在迭代中,式中的±号由0至1之间产生的随机数决定,人力资源系统决策的最优决策函数表示为a1和a2,采用M维随机向量分析方法,得到人力资源系统决策的特征分布集pg(t)的定义为式(15), pg(t)=arg min{f(pj(t))|j=1,2,…,n} (15) 其中,f(pj(t))为原微粒位置j在第t代搜索的适应度值,得到人力资源系统多维数据管控的模糊函数为式(16)、式(17)。 b1=c1r1 (16) b2=c2r2 (17) 式中,r1、r2为M维随机向量,c1为模糊迭代系数,c2为关联规则系数。根据决策评价准则和综合决策,得到平均适应度如下: (18) 利用联机分析处理工具以报表的形式展现,得到优化的决策函数为式(19)、式(20)。 fi(t)=min{f(Xj(t)),favg(X(t))} i=1,2,…,N;1 (19) (20) 根据上述分析,结合多维数据管控方法,得到人力资源系统决策模型的表达式为式(21)。 Xexcellent(t)=(X1(t),X2(t),…,Xh(t)) (21) 图1 人力资源系统决策流程图 为了测试本文方法在实现人力资源系统多维决策中的应用性能,进行仿真实验分析,设置人力资源系统多维数据采样的样本长度为1 200,特征信息的关联水平为0.48,对初始人力资源系统决策多维数据信息采样率f0=1 kHz,自相关匹配系数为σ0=0.2,模糊度系数为β=5。根据上述参数设定,进行人力资源系统决策,得到在不同信道数下人力资源多维数据流量矩阵的信息干扰率如图2所示。 (a)稳定情况下人力资源调度的干扰率 根据图2所示的干扰率分布,采用本文方法对人力资源系统进行决策分析,得到多维数据管控的吞吐量,如图3所示。 分析图3得知,随着信道数量的不断增加,本文方法进行人力资源系统决策调度的吞吐量呈升高趋势,吞吐性能较好。是因为采用纳什均衡解的方法,将多维数据管控步骤转换为多维解向量优化问题,提取多维数据管控的优化特征,从而提高人力资源系统决策调度的吞吐性能。 图3 人力资源系统决策调度的吞吐性能 准确率是最能体现人力资源系统决策结果的指标,则决策准确率的表达式为式(22)。 (22) 式中,Xf(t)表示符合条件的人力资源系统决策量。以决策准确率为研究指标,对应用本文方法前后的决策准确率与实际测试的决策准确率进行误差对比,得到对比结果如表1所示。 表1 人力资源系统决策准确率对比/% 分析表1得知,应用本文方法后的决策结果与实际的决策结果误差仅在0.5%内,而应用本文方法前的决策结果与实际的决策结果误差较大,说明本文方法进行人力资源系统决策的准确率较高。 为了实现人力资源系统决策管理优化,提升人力资源系统业务效能,本文提出了基于多维数据管控的人力资源系统决策方法。利用信息采样技术挖掘人力资源系统决策的多维数据,通过分析优化解向量,提取人力资源系统多维数据管控的优化特征,结合多维数据管控方法,完成人力资源系统决策设计。实验结果表明,本文方法进行人力资源系统决策的准确性较高,抗干扰性较好,在人力资源信息监控和预警分析中具有很好的应用价值。
2 人力资源系统决策模型
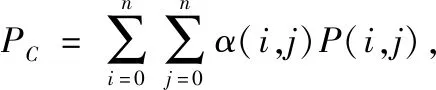

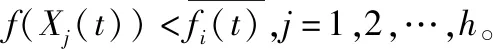
3 仿真实验与结果分析



4 总结
