阻尼间隙可调式磁流变阻尼器设计与动力性能实验

2022-02-21黄鑫芳胡国良

农业机械学报 2022年1期

左强黄鑫芳易锋童旺胡国良

(1.浙大城市学院工程学院，杭州 310015； 2.浙江中通通信有限公司，杭州 310014;3.华东交通大学载运工具与装备教育部重点实验室，南昌 330013)

0 引言

磁流变液是一种由磁性颗粒、载液以及添加剂组成的新型智能材料[1]。磁流变液具有磁流变效应,即其流变性能随着外加磁场变化而变化。当施加外加磁场时，磁流变液在毫秒时间内由普通牛顿液体迅速变为类固体，其剪切屈服应力与磁场强度有关；当外加磁场消失时，立刻由类固体转变成普通牛顿液体，且该过程连续可逆[2-3]。磁流变液优异的流变特性使其广泛应用于桥梁、建筑、车辆及机器人等领域[4-5]。

磁流变阻尼器是一种典型的以磁流变液为传动介质的半主动智能器件，主要由活塞杆、活塞头、励磁线圈及缸体等组成[6]。外界的振动推动活塞杆往复运动，内部的磁流变液在磁场的作用下发生磁流变效应，从而输出阻尼力。由线圈中电流控制磁场的强弱，因此磁流变阻尼器具有阻尼连续可控、响应速度快、成本低等优点[7]。

在磁流变阻尼器的结构设计方面，KIM等[8]对传统液流通道进行改进，提出一种具有分叉流动模式的磁流变阻尼器，其特点在于利用磁芯上的反馈孔径将内、外液流通道连接起来。实验结果表明该磁流变阻尼器具有更大的可控阻尼力和等效阻尼。LIAO等[9]设计了一种多级径向通道的旁路式磁流变阻尼器，多级径向通道延长了有效阻尼间隙长度，同时改善了磁场利用率不高的问题。实验结果证明该阻尼器具有更好的动力性能，但该方法使得磁流变阻尼器的轴向长度增大。ZEMP等[10]通过延长阻尼通道，设计了一种具有较大行程的磁流变阻尼器，并将其应用在21层的建筑上进行实验分析。ZHU等[11]将圆环液流通道与圆盘液流通道结合，提出一种多液流通道的磁流变阻尼器，结果表明该阻尼器阻尼力达到3.5 kN，具有良好的阻尼性能。YAZID等[12]提出一种具有剪切与挤压模式的磁流变阻尼器，实验表明混合模式下阻尼器的输出阻尼力大于单一模式下的输出阻尼力，但采用挤压模式的磁流变阻尼器存在结构复杂、加工难度大、成本高等问题。SOLOMON等[13]针对六轴式磁流变假肢膝关节设计了一种阀式磁流变阻尼器，在限制阻尼器最大长度和半径的基础上，利用基于响应曲面法的有限元设计方法对该阻尼器进行优化设计。结果表明该阻尼器相较于一般的阻尼器减轻了71%，并且能满足在假肢膝关节等安装体积小、行程短的环境下的使用。CHENG等[14]设计了一种具有曲折磁路的磁流变阻尼器，该阻尼器在幅值0.062 8 m/s的正弦速度激励下，输出阻尼力可达到3 400 N。HU等[15]为延长阻尼通道有效长度，在固定结构尺寸的前提下，利用3个不导磁套筒和4个导磁套筒将液流通道分割成3段串联式的液流通道。实验结果表明该串联式磁流变阻尼器最大阻尼力为6 838 N，等效阻尼系数达到290 kN·m/s。

上述提高磁流变阻尼器动力性能的方法主要包括延长液流通道、改变活塞头结构、优化磁路及增加线圈个数等，但从原理来说都是在保证阻尼间隙不变的前提下延长了有效阻尼长度[16]。虽然在不同程度上提高了磁流变阻尼器的动力性能，但也不可避免产生一些问题，如结构体积大、阻尼力较小、动力性能固定单一、适应性不强。在调整有效阻尼间隙方面[17]，ZHENG等[18]提出了一种阻尼间隙可调的多线圈式磁流变阻尼器，并利用二次近似边界优化算法对包括电磁场和流场的多物理场进行优化设计。但该阻尼间隙随活塞杆的位置变化而变化，故其阻尼力可调范围受活塞杆位置的影响。SONG等[19]提出一种具有不同阻尼间隙的磁流变制动器，但实验结果表明在不同的电流下，可调阻尼间隙对该制动器的制动转矩影响很小。HU等[20]为提升磁流变阀的动力性能，设计了一种阻尼间隙可在1～2 mm内连续可调的磁流变阀。该磁流变阀压降可调范围为130～1 150 kPa，可替代多种阻尼间隙固定的磁流变阀，但无运动部件、可控压降较小。

本文提出并设计一种阻尼间隙可调式磁流变阻尼器。该阻尼器液流通道由圆锥液流通道和圆环液流通道共同组成；通过调整紧锁螺母控制阀芯位置，改变阀芯与左右磁轭的相对位置，可以实现圆锥液流通道阻尼间隙连续可调。对该阻尼器分别进行结构设计、磁路分析、力学模型建立及电磁场仿真分析，同时对其动力性能进行测试分析。

1 结构设计

1.1 结构原理

图1为阻尼间隙可调式磁流变阻尼器结构示意图，主要由紧锁螺母、端盖、缸筒、阀芯、磁轭、励磁线圈、隔磁环、活塞杆、缸体及浮动活塞等组成。左磁轭、隔磁环及右磁轭共同组成活塞头，励磁线圈均匀缠绕在活塞头上。活塞头分别通过左缸筒和右缸筒进行固定，左、右缸筒上开有通孔。紧锁螺母与阀芯通过螺纹连接，通过调整紧锁螺母可改变阀芯的轴向位置，从而改变圆锥液流通道的阻尼间隙。

图1 阻尼间隙可调式磁流变阻尼器结构示意图Fig.1 Schematic of MR damper with adjustable damping gaps1.紧锁螺母 2.左端盖 3.左缸筒 4.阀芯 5.左磁轭 6.励磁线圈 7.隔磁环 8.右磁轭 9.活塞杆 10.右缸筒 11.缸体 12.浮动活塞 13.右端盖

紧锁螺母顺时针拧紧时，阀芯沿轴线右移使得阀芯与活塞头之间的相对距离减小，从而减小圆锥液流通道的阻尼间隙。当紧锁螺母逆时针拧松时，阀芯沿轴线左移使得阀芯与活塞头之间的相对距离增大，从而增大圆锥液流通道的阻尼间隙。图2为最大和最小阻尼间隙下液流通道分布图。阀芯伸出长度l为最大值lmax时，阻尼间隙达到最大值h2max；阀芯伸出长度为最小值lmin时，阻尼间隙达到最小值h2min。圆锥液流通道有效阻尼间隙可表示为

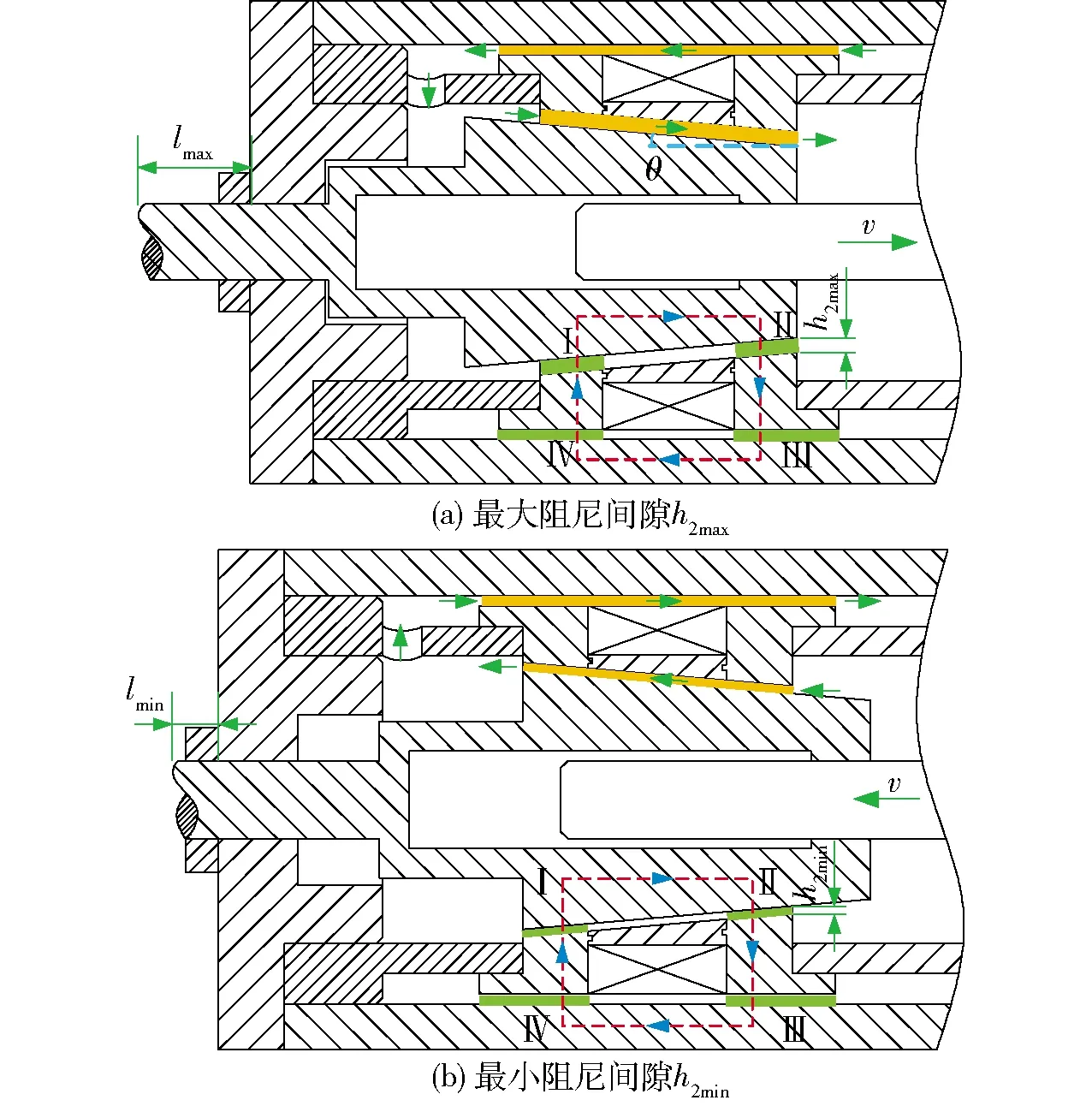
图2 不同阻尼间隙下液流通道分布图Fig.2 Distributions of fluid flow paths under different damping gaps

h2=h2min+(l-lmin)tanθcosθ≈
h2min+(l-lmin)θ

(1)

其中

(2)

式中h2——圆锥液流通道阻尼间隙

θ——圆锥液流通道半锥角

该结构在不增加结构尺寸和安装空间的前提下，在阻尼间隙固定的圆环液流通道的基础上集成圆锥液流通道，不仅延长磁流变阻尼器的有效阻尼长度，而且使有效阻尼间隙连续可调。

工作时阻尼器由于受到外界振动使活塞杆往复运动。活塞杆向右运动为拉伸，向左运动为压缩。阻尼器分别处于拉伸和压缩时，磁流变液流向如图2所示。励磁线圈输入激励电流产生磁场，其磁力线从阀芯出发，经过圆锥液流通道、左磁轭、圆环液流通道、缸体及右磁轭，最后回到阀芯形成闭合回路。磁力线垂直穿过圆锥液流通道和圆环液流通道形成4段有效阻尼间隙Ⅰ、Ⅱ、Ⅲ及Ⅳ。磁流变液流经该间隙发生磁流变效应，产生与磁场相关的剪切屈服应力，从而使磁流变阻尼器输出可控阻尼力。表1为阻尼间隙可调式磁流变阻尼器的关键结构参数。

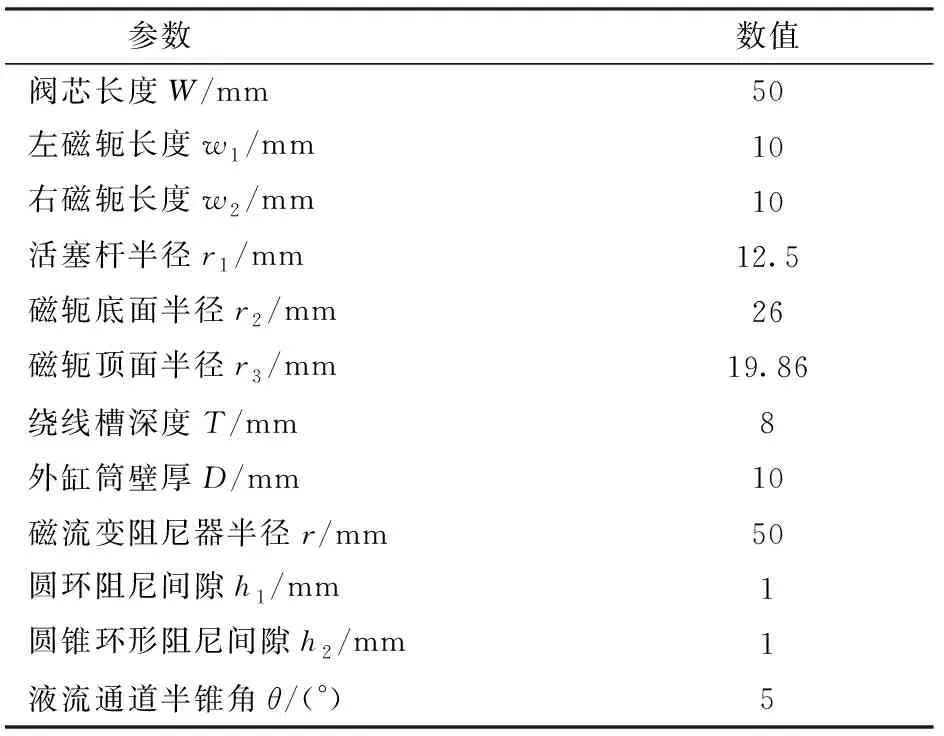
表1 MRD关键结构参数Tab.1 Key structure parameters of MRD

1.2 磁路设计

图3为磁路示意图。基于磁路欧姆定律，磁动势可表示为

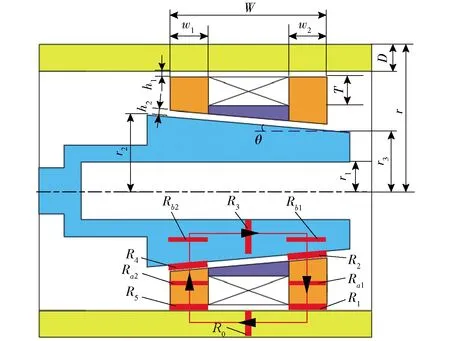
图3 磁路示意图Fig.3 Simplified magnetic circuit

NI=∮HdL=Rmφ

(3)

其中

φ=BS

(4)

式中N——励磁线圈匝数

I——励磁线圈中的激励电流

H——磁场强度

L——磁力线穿过的长度

Rm——磁路总磁阻

φ——磁通量

B——磁感应强度

S——磁力线穿过区域面积

磁阻R可表示为

(5)

式中μ——材料导磁率

由图3可知，总磁阻Rm相当于各部分磁阻依次串联，可表示为

Rm=R0+R1+(Ra1+Rb1)+R2+
R3+R4+(Ra2+Rb2)+R5

(6)

缸体磁阻R0为

(7)

缸体左侧与左磁轭间的阻尼间隙磁阻R1为

(8)

阀芯左翼磁阻Ra1与左磁轭磁阻Rb1之和为

(9)

左磁轭与阀芯左侧间阻尼间隙R2为

(10)

阀芯磁阻R3为

(11)

右磁轭与阀芯右侧间阻尼间隙R4为

(12)

阀芯右翼磁阻Ra2与右磁轭磁阻Rb2之和为

(13)

缸体右侧与右磁轭间的阻尼间隙磁阻R5为

(14)

式中V——阀芯有效体积

μ1——10#钢的相对磁导率

μ2——磁流变液的相对磁导率

μ3——真空绝对磁导率

2 力学模型

图4为阻尼间隙可调式磁流变阻尼器的压降分布示意图。当阻尼器处于拉伸状态时，由于右侧压强小于左侧压强，使得磁流变液由左侧往右侧流动。阻尼器工作时励磁线圈通入电流使得圆锥液流通道Ⅰ、Ⅱ和圆环液流通道Ⅲ、Ⅳ处的磁流变液发生磁流变效应，从而产生可控压降。该阻尼器的工作模式为流动模式，其总压降为各部分压降之和，即

图4 压降分布示意图Fig.4 Schematic of distribution of pressure drop

Δp=Δp1+Δp2+Δp3+Δp4

(15)

式中 Δp1、Δp2、Δp3、Δp4——圆锥液流通道Ⅰ、Ⅱ和圆环液流通道Ⅲ、Ⅳ处的压降

由于圆环液流通道Ⅲ、Ⅳ相对励磁线圈对称，磁场分布相同，故两处压降相等，即

Δp3=Δp4

(16)

根据Bingham模型，圆环液流通道Ⅲ处的压降Δp3为

Δp3=Δpη3+Δpτ3=

(17)

式中 Δpη3——圆环液流通道Ⅲ处的粘滞压降

Δpτ3——圆环液流通道Ⅲ处的库仑压降

η——磁流变液黏度

A——活塞面积

v——磁流变液运动速度

b——磁流变液展开宽度

c——修正参数，取3

τ3——圆环液流通道Ⅲ处磁流变液的剪切屈服应力

将锥形液流通道展开，其截面形状呈扇形，如图5所示。圆心角α可表示为

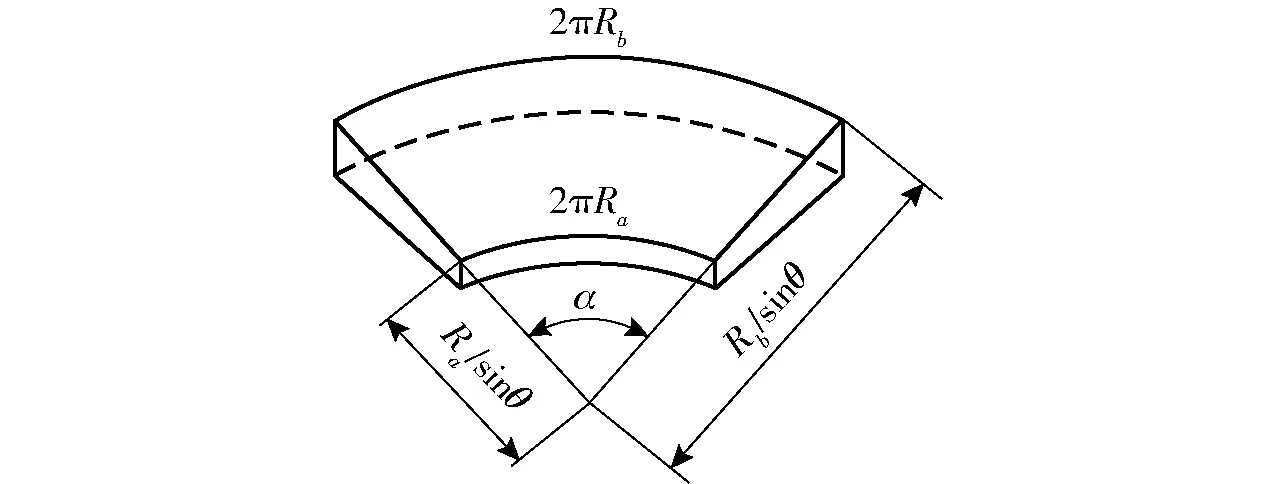
图5 圆锥液流通道等效图Fig.5 Equivalent schematic of conical fluid flow

α=2πsinθ

(18)

圆锥液流通道Ⅰ处的压降Δp1为

(19)

式中 Δpη1——圆锥液流通道Ⅰ处的粘滞压降

Δpτ1——圆锥液流通道Ⅰ处的库仑压降

Ra、Rb——圆锥小径和大径

τ1——圆环液流通道Ⅰ处磁流变液的剪切屈服应力

同理，圆锥有效阻尼间隙Ⅱ处的压降Δp2为

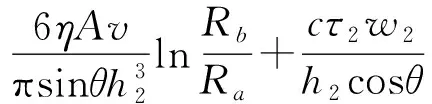
(20)

式中 Δpη2——圆锥液流通道Ⅱ处的粘滞压降

Δpτ2——圆锥液流通道Ⅱ处的库仑压降

τ2——圆环液流通道Ⅱ处磁流变液的剪切屈服应力

根据式(15)～(20)可得阻尼间隙可调式磁流变阻尼器的总压降Δp为

(21)

故阻尼间隙可调式磁流变阻尼器的输出阻尼力F为

F=ΔpA=Fη+Fτ

(22)

式中Fη、Fτ——粘滞阻尼力、库仑阻尼力

可调系数K定义为输出阻尼力F与粘滞阻尼力Fη比值，即

(23)

3 电磁场仿真分析

为验证所设计的阻尼间隙可调式磁流变阻尼器结构参数是否合理，同时确定各个有效阻尼间隙处剪切屈服应力，利用ANSYS软件对磁流变阀的结构进行电磁场仿真。在保证求解精度的前提下，根据磁流变阀的几何特性选取其1/2平面模型进行建模。图6为磁流变阀的有限元模型，主要包括不锈钢、10#钢、励磁线圈及磁流变液。其中，10#钢和磁流变液分别为高导磁材料和弱导磁材料，其导磁率根据其B-H曲线得出；不锈钢和励磁线圈为不导磁材料，其导磁率设为1。

图6 磁流变阀有限元模型Fig.6 Finite element model of MR valve

图7为磁流变阀的磁力线分布图。由图7可知，磁力线主要分布在主磁路内，仅少数磁力线没经过圆环有效阻尼间隙和圆锥有效阻尼间隙；磁力线集中分布在励磁线圈周围，越靠近励磁线圈的地方磁力线越密集；主磁路磁力线几乎垂直穿过圆环有效阻尼间隙和圆锥有效阻尼间隙，少数接近励磁线圈处的磁力线为未垂直穿过有效阻尼间隙，主要由于缸体、左缸筒和左右磁轭为导磁材料。图8为磁流变阀的磁感应强度分布图。由图8可知，圆环有效阻尼间隙和圆锥有效阻尼间隙处的磁感应强度较大；磁感应强度最大值分布在圆锥有效阻尼间隙Path1处，与图7中磁力线的分布规律吻合。

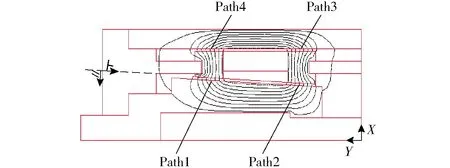
图7 磁力线分布图Fig.7 Distribution of magnetic flux lines

图8 磁感应强度分布图Fig.8 Contours of magnetic flux density

圆环液流通道两侧相对励磁线圈对称，由图7、8可知，圆环有效阻尼间隙Path3与Path4处的磁感应强度相等。由于圆锥有效阻尼间隙Path1与Path2不与坐标轴重合(X、Y为二维模型的坐标轴)，因此将后处理得到磁感应强度处Bx、By分解为垂直有效阻尼间隙的磁感应强度Bv与平行有效阻尼间隙的磁感应强度Bn，可表示为

Bv=Bxcosθ-Bysinθ

(24)

Bn=Bxsinθ+Bycosθ

(25)

图9a为圆锥有效阻尼间隙Path1磁感应强度分布曲线。由图可知，垂直有效阻尼间隙的磁感应强度Bv基本稳定在-0.52 T，负号代表磁感应强度方向与设定方向相反；平行有效阻尼间隙的磁感应强度Bn基本为0。由于θ很小，在保证阻尼间隙可调前提下可使磁力线尽可能垂直穿过有效阻尼间隙。另外，Path1在0、13 mm处磁感应强度变化较大，这是由于该部分磁力线不垂直穿过圆锥有效阻尼间隙。图9b为圆锥有效阻尼间隙Path2磁感应强度分布曲线。与图9a类似，垂直有效阻尼间隙的磁感应强度Bv基本稳定在0.51 T，平行有效阻尼间隙的磁感应强度Bn基本为0。Path1的垂直有效阻尼间隙的磁感应强度Bv略大于Path2，这是由于Path1比Path2更靠近励磁线圈。

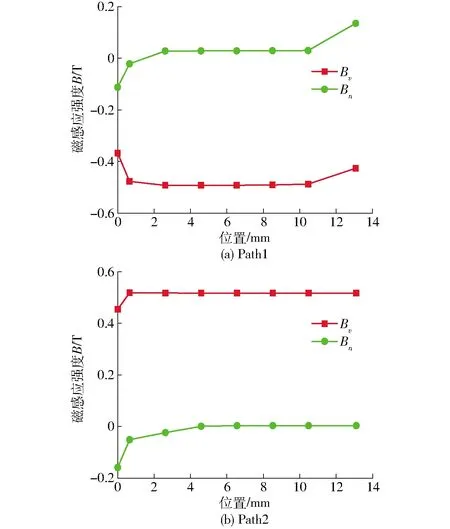
图9 不同路径下磁感应强度分布曲线Fig.9 Distribution of magnetic flux density along different paths

为得到电流与有效阻尼间隙处剪切屈服应力的数学关系，对路径上的各点磁感应强度进行积分并除以路径长度，得到阻尼间隙可调式磁流变阻尼器的磁感应强度B为

(26)

式中B(x)——路径上各点的磁感应强度

x——路径单位长度

图10a、10b为不同阻尼间隙下圆锥液流通道Path1、Path2的磁感应强度与电流曲线，在有效阻尼间隙为0.6～1.6 mm内，磁感应强度随有效阻尼间隙的减小而增大，并且在阻尼间隙为1 mm附近变化明显；当阻尼间隙和电流不变时，Path1处磁感应强度大于Path2处磁感应强度；电流为1 A时，不同阻尼间隙下Path1磁感应强度分布在0.41～0.52 T之间，而Path2磁感应强度分布在0.39～0.51 T之间。图10c为圆环液流通道Path3(Path4)的磁感应强度变化曲线。由图可知，电流为1 A时，Path3(Path4)的磁感应强度为0.43 T，略小于阻尼间隙为1 mm时圆锥液流通道Path1、Path2磁感应强度。

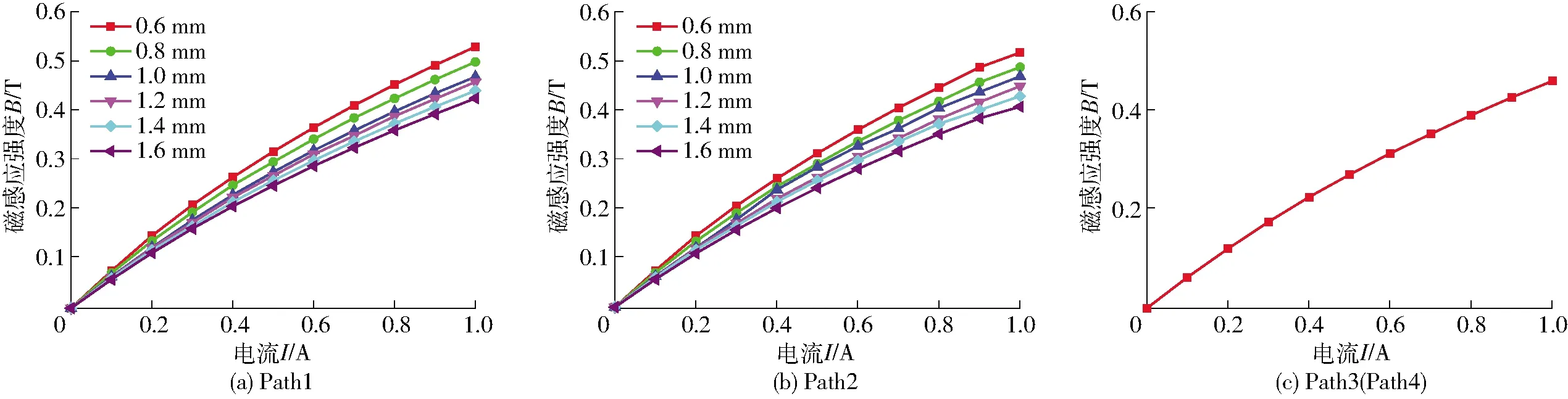
图10 不同路径下磁感应强度变化曲线Fig.10 Magnetic flux density along different paths

磁流变液由重庆材料研究所研制，型号为MRF-J01T，其剪切屈服应力τ与磁感应强度B的关系可表示为

τ=a1B3+a2B2+a3B+a4

(27)

式中a1、a2、a3、a4——多项式拟合参数

取a1=-984.27 kPa/T3,a2=865.39 kPa/T2,a3=-48.46 kPa/T和a4=0.018 kPa。

由式(27)和图10可确定剪切屈服应力τ与电流I的关系，代入式(22)磁流变阻尼器的力学模型中可以得到阻尼力与电流的表达式。施加位移激励频率为1 Hz、振幅为15 mm的正弦信号，图11为不同阻尼间隙下阻尼力F随电流I的变化曲线。由图11可知，当电流固定时，阻尼力随阻尼间隙减小而增大，并且增加趋势越来越明显；当阻尼间隙固定时，阻尼力随电流增大而增大。当电流为1 A，不同阻尼间隙下阻尼力为0.2～9.6 kN。

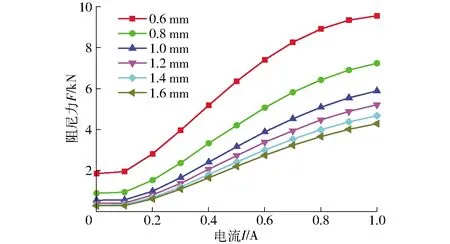
图11 不同阻尼间隙下阻尼力随电流的变化曲线Fig.11 Relationship between damping force and current under different damping gaps

图12为可调系数K随阻尼间隙的变化曲线。由图12可知，可调系数K随阻尼间隙的增大而增大，但慢慢趋近平缓；阻尼间隙为1.6 mm时，最大可调系数K为14.4。

图12 可调系数随阻尼间隙的变化曲线Fig.12 Relationship between adjustable coefficient and damping gap

4 性能测试分析

图13为加工的阻尼间隙可调式磁流变阻尼器样机。磁流变阻尼器实验测试系统如图14所示，主要由直流电源、疲劳拉伸机、磁流变阻尼器、数据采集卡及计算机组成。其中，疲劳拉伸机产生不同的正弦激励使磁流变阻尼器往复运动；直流电源为磁流变阻尼器供电；疲劳拉伸机上装有位移传感器和力传感器等，采集到的信号通过数据采集卡传输到计算机。实验过程中将装配好的阻尼间隙可调式磁流变阻尼器左吊耳装夹在疲劳拉伸机的动力杆上，右吊耳装夹在疲劳拉伸机的工作台上。设置不同的位移激励并控制直流电源为励磁线圈通入电流，分别改变阻尼间隙可调式磁流变阻尼器的阻尼间隙进行动力特性实验。

图13 阻尼间隙可调式磁流变阻尼器样机Fig.13 Prototype of MR damper with adjustable gaps

图14 磁流变阻尼器实验测试系统Fig.14 Experiment test rig of proposed MR damper

图15为阻尼间隙1 mm、激励幅值4 mm、频率0.4 Hz时，不同加载电流下的阻尼力-位移变化曲线。由图可知，阻尼力与位移变化曲线呈回字形。图16为不同加载电流下的阻尼力-速度关系曲线。当速度固定时，阻尼力均随电流的增加而增加；阻尼力增加趋势越来越平缓，说明磁路慢慢接近饱和。当电流固定时，阻尼力几乎随速度的增加而增加；当电流为1.0 A时，最大阻尼力为4.3 kN，当电流为0 A时，粘滞阻尼力为0.2 kN。

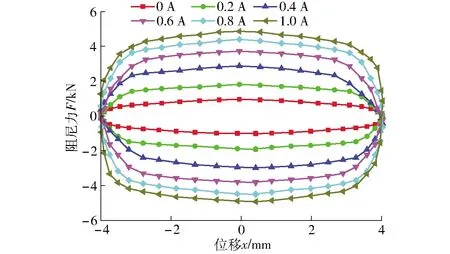
图15 不同电流下阻尼力-位移关系曲线Fig.15 Relationship curves of damping force and displacement under different currents

图16 不同电流下阻尼力-速度关系曲线Fig.16 Relationship curves of damping force and velocity under different currents

图17为固定电流0.8 A、阻尼间隙1 mm、激励频率0.4 Hz时，不同激励幅值下的阻尼力-位移变化关系曲线。由图可知，阻尼力随激励幅值的增加而略微增加，这是由于激励频率固定时，增加幅值将增加阻尼器运动速度，故使得阻尼力略微增加。当激励幅值为4 mm时，最大阻尼力达到4.3 kN，而当激励幅值为8 mm，最大阻尼力达到5.1 kN。

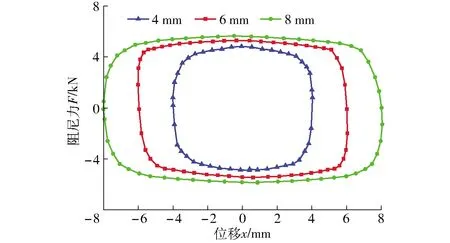
图17 不同激励幅值下阻尼力-位移关系曲线Fig.17 Relationship curves of damping force and displacement under different amplitudes of excitation

图18为固定电流0.8 A、阻尼间隙1 mm、激励幅值4 mm时，不同激励频率下的阻尼力-位移变化关系曲线。由图可知，阻尼力随激励频率的增加而略微增加。这是由于激励幅值固定时，增加频率将增加阻尼器运动速度，故使得阻尼力略微增加。当激励频率为0.4 Hz时，最大阻尼力达4.3 kN；当激励幅值为0.8 Hz，最大阻尼力达4.9 kN。

图18 不同激励频率下阻尼力-位移关系曲线Fig.18 Relationship curves of damping force and displacement under different frequencies of excitation

图19为固定电流0.8 A、激励幅值4 mm、频率0.4 Hz时，不同有效阻尼间隙下阻尼力-位移关系曲线。由图20可知，当速度固定时，阻尼力随有效阻尼间隙的减小而增加；在阻尼间隙为1 mm附近，在不同阻尼间隙下阻尼力变化相对明显。初步说明有效阻尼间隙对阻尼力有较大影响(尤其在1 mm左右)。

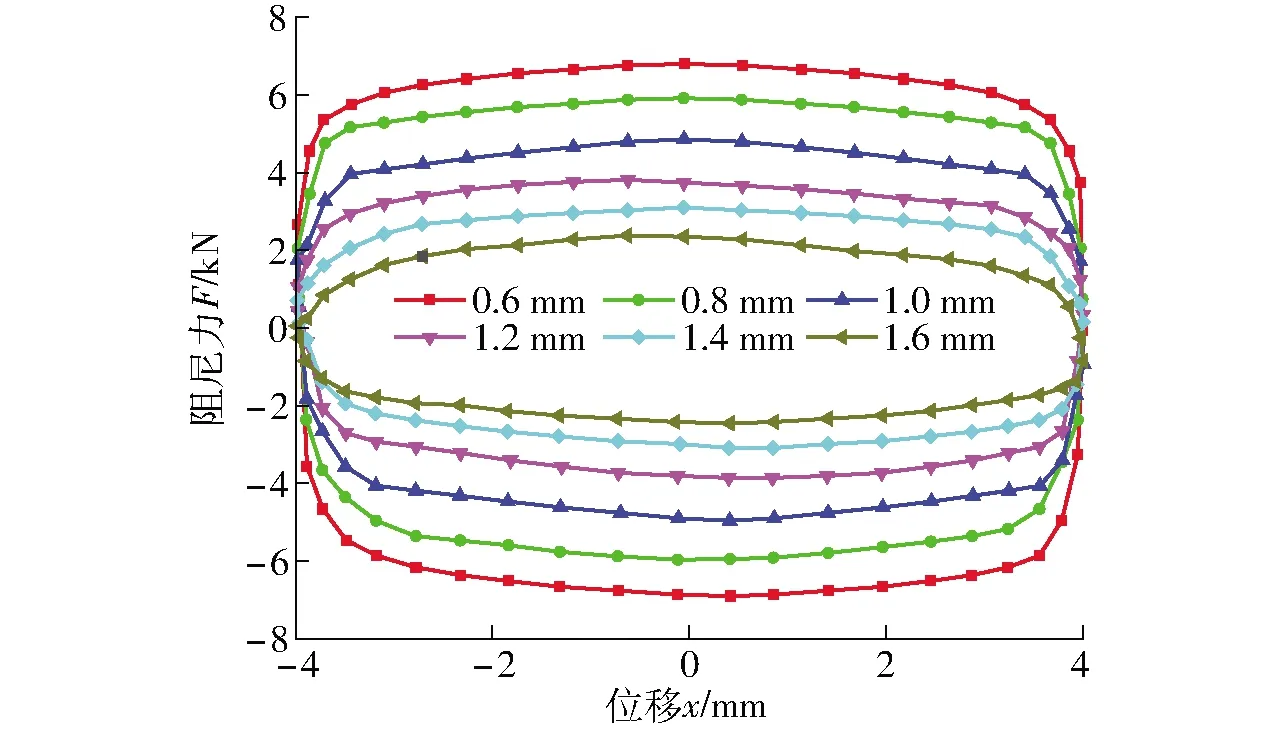
图19 不同阻尼间隙下阻尼力-位移关系曲线Fig.19 Relationship curves of damping force and displacement with different adjustable gaps

激励幅值为4 mm、频率为0.4 Hz时，分别改变电流与圆锥液流通道的阻尼间隙，得到图20所示的不同电流下阻尼力-阻尼间隙变化关系曲线。由图20可知，当阻尼间隙固定时，阻尼力随电流的增大而增加；当固定电流时，阻尼力随阻尼间隙的增加而减小，并且在阻尼间隙0.6～1.2 mm内的减小趋势大于在阻尼间隙1.2～1.6 mm内。

图20 不同电流下阻尼力-阻尼间隙关系曲线Fig.20 Relationship curves of damping force and damping gap under different currents

图21为不同阻尼间隙下阻尼力-电流关系曲线。当阻尼间隙固定时，阻尼力随电流的增大而增加，但增加趋势越来越小，说明磁路慢慢接近饱和。图22为阻尼力可调范围曲线，其中粘滞阻尼力和库仑阻尼力均随阻尼间隙增大而减小。当电流为0 A时，阻尼间隙为1.6、0.6 mm时的阻尼力分别为0.2 kN和1.3 kN(粘滞阻尼力)，而当电流为1 A时，最大阻尼力分别为2.9 kN和7.2 kN。

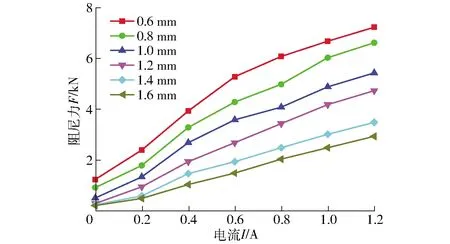
图21 不同阻尼间隙下阻尼力-电流关系曲线Fig.21 Relationship curves of damping force and current under different damping gaps

图22 阻尼力可调范围曲线Fig.22 Regulating range of damping forces

根据图21的不同阻尼间隙下阻尼力-电流曲线，得到不同阻尼间隙下可调系数曲线如图23所示。可调系数K随着阻尼间隙的增大而增大。当阻尼间隙为1.6 mm时，可调系数达到13.6，而当阻尼间隙为0.6 mm时，可调系数为5.9。

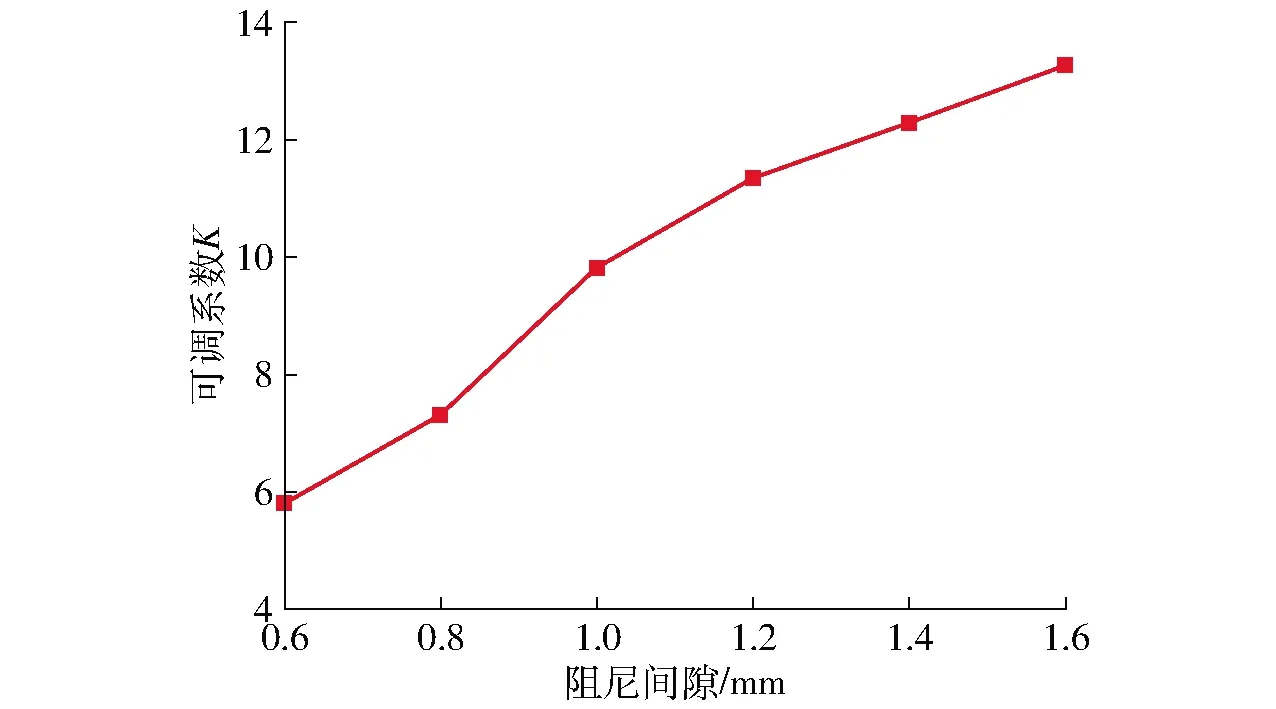
图23 不同阻尼间隙下可调系数曲线Fig.23 Adjustable coefficient curve with different damping gaps

由图21、23可知，阻尼力随阻尼间隙的增大而减小，可调系数随阻尼间隙的增大而增大。在不同阻尼间隙下，阻尼力为0.2～7.2 kN，可调系数达到33。故针对一般情况，将阻尼间隙设置为1.0 mm可实现较大的阻尼力和可调系数，这与一般延长阻尼长度的磁流变阻尼器效果相同。然而针对不同应用场合，对阻尼力、可调系数的要求不同，如高档山地车等需要较大的可调系数、适中的阻尼力；而大型客车、抗风桥梁等需要较大的阻尼力和较低的可调系数，此时阻尼间隙固定的磁流变阻尼器难以同时适用上述场合。而本文设计的阻尼间隙可调式磁流变阻尼器通过灵活调整圆锥液流通道阻尼间隙，可同时适用上述场合。因此，本文设计的阻尼间隙可调式磁流变阻尼器可以替代多种阻尼间隙固定的传统磁流变阻尼器，极大地提升了磁流变阻尼器的动力性能。