基于多传感器融合的跟随AGV复合导引技术

钱晓明 黄宇轩 楼佩煌 孙 天

(南京航空航天大学机电学院， 南京 210016)

0 引言

自动导引小车(Automated guided vehicle, AGV)是一种沿指定路径自动行驶，在不同工位点之间进行物料搬运的轮式移动机器人[1]，广泛应用于工业生产和物流运输[2]。随着AGV应用场景需求的复杂化，多AGV协同搬运是机器人技术发展的必然趋势。多台AGV协同搬运可以突破单台AGV尺寸、承载方式和载荷量等限制，充分发挥AGV的运输能力和编队协作灵活性。目前，多AGV协同大多采用“主从式”(Leader-Follower)的编队策略。

导引技术是保证AGV自主性和移动性的关键技术。对于“主从式”双车协同搬运系统，领航AGV的导引方式与单台AGV类似，技术上已趋于成熟；跟随AGV的定位和导引，除了获取环境信息之外，还需要观测领航AGV进行路径跟随，对精度和稳定性有更高的要求。目前广泛采用的AGV导航技术在定位精度、导引灵活性、运行可靠性和使用成本等多种指标之间难以取得较好的协调平衡。当前复合导引大多采用GPS导航、惯性导航、视觉导航等导航技术中的若干种，通过数据融合算法综合多种异构多源传感器采集的信息，使AGV导引更为稳定可靠。

多传感器融合技术[3-4]是将多种传感器的信息进行综合，输出与真实值较为接近的观测信息，实现各传感器的优势互补。视觉里程计和IMU的数据融合又称为视觉惯性里程计(Visual inertial odometry, VIO)，根据数据融合方式的差异可以分为紧耦合和松耦合两种[5]。KONOLIGE等[6]通过扩展卡尔曼滤波(Extended Kalman filter,EKF)对惯导-视觉系统进行松耦合，提高了视觉里程计的精度。INDELMAN等[7]基于因子图的惯导增量平滑方式，提出一个通用的信息融合框架。MOURIKIS等[8]提出了多状态限制卡尔曼滤波(Multi-state constraint Kalman filter, MSCKF)算法，为VIO提供了第一个紧耦合框架。LI等[9]通过改进算法提高了MSCKF的实时性。TSAO等[10]提出基于EKF算法、视觉-惯导融合的相机参数标定方法。除了科研机构外，一些大型设备制造商也开展了视觉/惯导的相关研究，例如苹果公司推出的ARKit，将单目视觉和惯导信息通过EKF进行融合。随着智能化的深入，视觉里程计/惯导结合的多传感器融合技术已成为机器人领域热门的研究方向。

本文基于Leader-Follower编队中跟随式AGV的定位和导引需求，提出一种视觉/惯导组合导航方案，其中视觉系统采用路径跟踪导航和RGB-D导航相结合的多目视觉导航。针对多目视觉系统和惯性导航的数据融合问题，提出一种基于AUKF算法的跟随AGV最优位姿估计方法，以保障跟随AGV复合导引的精度和稳定性。

1 复合导引方案设计

AGV的导引和定位方式可以分为绝对定位方式和相对定位方式[11]。考虑到双车协同搬运中跟随AGV在编队中的导引需求，将相对定位与绝对定位方式相结合。跟随AGV的复合导引方案如图1所示。惯性导引作为一种成熟的相对定位方法，采样频率高、抗干扰性强，能够满足AGV位姿估计实时性和准确性的需求。但其在测量数据时存在累积误差，一般用于短时位姿的估计，不能单独使用。本文使用视觉导引作为绝对定位方式，与惯性导航配合，实现对惯导偏移误差的实时校正。

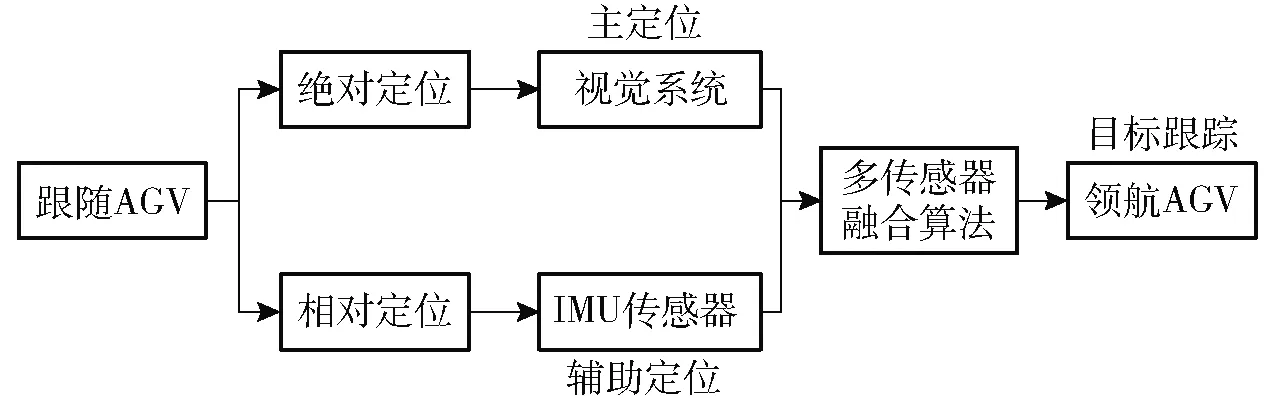
图1 跟随AGV复合导引方案Fig.1 Compound navigation scheme of following AGV

2 跟随AGV多目视觉导航方法

2.1 多目视觉导航技术框架

AGV协同搬运的工作场景多为复杂工况环境，如果选用单一的视觉传感单元会使跟随AGV感知信息不全面、易受外部环境影响，无法保证双车协同搬运系统长期稳定运行。本文提出一种路径跟踪导航与RGB-D视觉导航相结合的多目视觉导航方法，如图2所示。

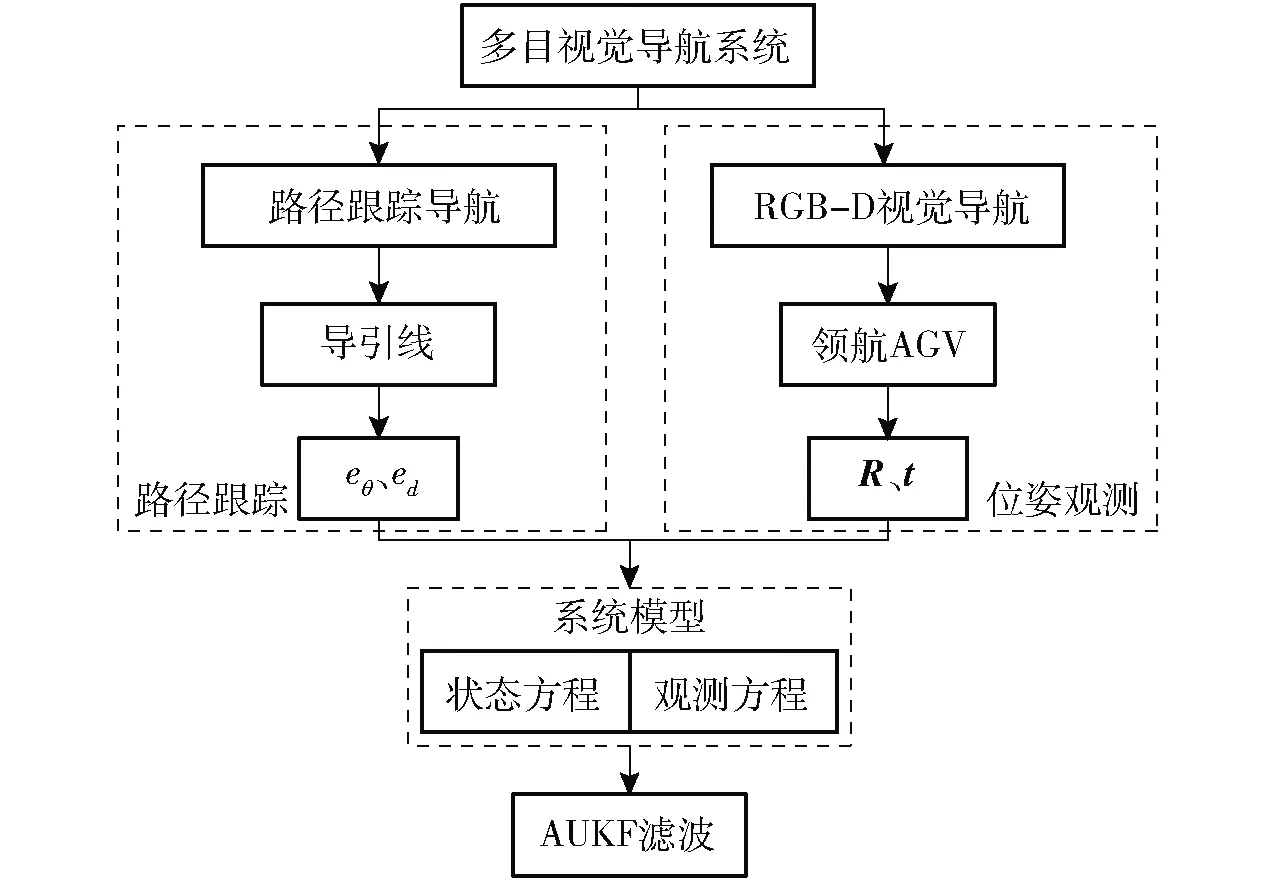
图2 多目视觉导航技术框架Fig.2 Framework of multi-vision navigation technology

跟随AGV的视觉系统布局如图3所示，本文多目视觉导航系统由路径跟踪导航方法和RGB-D视觉导航方法组成：

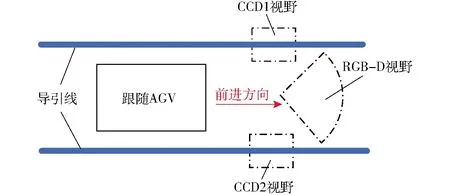
图3 跟随AGV视觉系统布局Fig.3 Visual system layout of following AGV

(1)路径跟踪导航方法。在AGV行驶路径上的两侧设置导引线，通过跟随AGV两侧安装的CCD摄像机采集导引线图像信息。两侧导引线限制跟随AGV在导引线划定的区域内运行。AGV路径跟踪导航技术目前发展比较成熟，本文不作重点描述。

(2)RGB-D视觉导航方法。RGB-D深度相机实时采集领航AGV的外壳轮廓图像，并匹配相邻两幅图像的特征点，通过ICP算法求取跟随AGV的相对位姿。

复杂环境同时影响两种视觉导航方法的可能性极小，可以认为任何时刻至少有一种视觉导航方法有效且稳定。受外界环境干扰时，其中一种视觉导航方法性能降低，另一种导航方法可以保证AGV平稳运行。多目视觉系统未受外界环境干扰时，两种导航方法的精度均得到保障。两种视觉导航信息相互融合和校正，可以获得尽可能全面、准确的外部环境观测。

2.2 路径跟踪导航

为保证跟随AGV具有较高的预测控制能力，车载相机倾斜向下安装。两侧CCD摄像机实时采集路径导引线的信息，经视频解码器解码后，输出至图像处理模块中处理。路径跟踪导航使用导引线，铺设在水磨石地面上，在YCbCr色彩空间下识别效果较好，故进行色彩空间转换，使用YCbCr图像中Cb分量进行阈值分割。

如图4所示，首先使用Otsu方法进行图像分割，得到路径导引线的二值化图像，经过形态学核运算获得较为光滑平整的路径轨迹轮廓，最后通过骨架提取算法提取路径特征，得到导引路径中心线。

图4 导引路径识别图像Fig.4 Recognition images of navigation path

直线导引路径可以用方程y=β0x+β1来表示，而曲线路径可以采用“以直代曲”思想视作多段较短的连续直线段拼接而成。对导引路径图像进行拟合，拟合结果如图5所示，并求解路径参数β0和β1。通过几何关系可以获取跟随AGV相对路径中心线的角度偏差eθ及距离偏差ed。

图5 路径拟合结果Fig.5 Result of path fitting

2.3 RGB-D立体视觉导航

RGB-D相机能够实时获取AGV的RGB图像和深度图像。RGB-D导航的位姿测量流程如图6所示。首先对原始图像进行预处理，通过阈值分割获得领航AGV的外壳轮廓。然后对相邻两帧图像进行特征点的提取和匹配，最后通过对点云数据的配准，得到深度相机的相对位姿(相机的旋转矩阵R和平移向量t)。由于深度相机固连在跟随AGV车身上，深度相机的运动轨迹与跟随AGV一致。实验选用Intel公司研发的RealSense D435i型深度相机。

图6 RGB-D导航位姿测量流程Fig.6 RGB-D navigation measurement process

2.3.1图像预处理和特征点检测

RGB立体视觉导航方法用于观测领航AGV，首先进行观测图像预处理。使用文献[12]中的最佳阈值分割方法来进行图像阈值的选取，通过阈值分割和平面提取算法分割出领航AGV的外壳轮廓。图像分割结果如图7所示。

图7 图像分割结果Fig.7 Result of image segmentation

完成对领航AGV外壳轮廓的分割后，对预处理后的图像进行特征点检测。考虑到双车协同搬运系统对实时性的要求，选择ORB(Oriented FAST and rotated BRIEF)特征点来进行领航AGV轮廓特征点的检测，特征提取后得到图像的ORB特征点集如图8所示。

图8 特征点检测结果Fig.8 Result of prominent points detection

2.3.2改进RANSAC特征点匹配

随机抽样一致(Random sample consensus, RANSAC)算法对于数据排异和提高模型估计精度有良好的效果[13]。传统RANSAC算法随机抽取特征点对迭代，算法复杂度较高；同时算法具有一定的随机性，不能保证特征点匹配的精度，为了提高匹配精度，必须提高迭代的次数。本文基于RANSAC算法提出一种改良算法，用于深度图像的特征点匹配。

改进RANSAC的特征点匹配算法具体实现步骤如下：

(1)特征点初始化

通过ORB特征点检测方法获得相邻两幅图像的特征点集。前一幅图像的特征点集X={xi∈X,i=1,2,…,n}，后一幅图像的特征点集Y={yi∈Y,i=1,2,…,n}。

(2)特征点粗匹配

ORB特征点通过汉明距离进行图像特征点匹配，在匹配过程中会存在一些错误匹配的特征点对。使用基于阈值的粗匹配算法初步过滤这些离群点：首先计算两幅图像特征点的汉明距离，采用FLANN算法进行特征点的配准，计算所有匹配点对的最近邻距离d1和次近邻距离d2。设定阈值T，如果两者的比值r=d1/d2小于T，则保留该匹配点对。本文T取0.7。

(3)双向交叉滤波筛选

通过步骤(2)可以得到粗匹配的图像，新的特征点集记作X′和Y′。由于RealSense D435i型相机对于深度值较大特征点的测量存在一定误差，因此采用双向交叉滤波方法对图像的特征点进行进一步筛选：在点集X′中寻找特征点xi，对应Y′中特征点yi。在点集Y′中寻找特征点yi，对应X′中特征点xi。基于反向传播匹配原理，如果特征点xi和yi在特征点集中互相对应，则认为是正确的匹配点对，保留该特征点对，否则予以筛除。

(4)余弦相似度提纯

针对步骤(3)双向滤波后仍存在的误匹配点对，引入余弦相似度的概念进行进一步过滤。两个特征向量间的余弦值越大，则特征向量相似程度越高。设两个特征向量X和Y之间夹角为θ，则余弦相似度可以表示为

(1)

式中cosθ的取值范围为[-1,1]，取值越接近1，这2个特征描述向量的相关性就越高。设定经验阈值Te。计算每一对特征点对应特征向量间的余弦相似度，如果c>Te，则接受该特征点对，否则予以剔除。经过该步骤得到精匹配的图像。

(5)使用RANSAC算法对错误匹配点对进行最后一次筛除。

(6)获得最终匹配完成的特征点对，用于后续的相机位姿估计。

为验证该特征点匹配算法的性能，与传统RANSAC算法进行图像匹配性能对比。特征点匹配结果如图9和表1所示。

图9 特征点匹配效果对比Fig.9 Comparison of matching effect of feature points

表1中改进RANSAC算法得到的匹配点数量少于传统RANSAC算法，说明改进RANSAC算法更有效地剔除了误匹配点对。在特征点提取过程中，定义特征点的期望个数为400，剔误率以原始ORB算法作为基准。改进RANSAC耗时较少，匹配速度相对RANSAC算法有所提升。在其他运行位置，特征点匹配结果也基本类似。从实验结果来看，改进RANSAC算法对于特征点匹配具有更高的实时性和匹配精度。

2.3.3相机位姿估计

使用ICP算法实现点云间的精确配准，得到深度相机的位姿估计。ICP算法的基本思路是在2组点云集合中找出最邻近点(xi,yi)，采用非线性优化的方式，通过位姿估计计算出最优匹配参数R和t，通过不断优化迭代直到误差小于某一阈值，以此确定最终的位姿估计。其中，相机的位姿通常使用李代数或四元数来表达。

从两组点云集合X″和Y″中取出点xi和yi，使得‖xi-yi‖取值最小。

求解R和t，使误差函数E(R,t)值最小。

(2)

采用李代数表达位姿，则位姿函数可以表示为

(3)

基于李代数扰动模型，单个误差项对位姿的导数可表示为

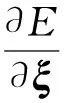
(4)

式中 ⊙——算符,定义为欧氏变化SE(3)上的李代数求导模型[14]

经过反复迭代运算，使得误差函数收敛到极小值。由文献[15]可知，当ICP存在唯一解时，该极小值即为全局最优解。在某些情况下，某些像素的深度数据获取可能出现缺失，ICP算法的精度难以得到保证。此时需要结合PnP算法进行3D-2D的点对运动求解，以获得较好的姿态估计。

3 多传感器融合算法和最优位姿估计

3.1 自适应无迹卡尔曼滤波

对于一个非线性系统，系统方程可以表示为[16]

(5)

式中k——某一时刻

Xk、Xk+1——k、k+1时刻系统状态向量

f——非线性系统状态转移函数

hk——观测变量到状态变量的转换关系

uk——当前时刻的外部指令输入

Zk+1——k+1时刻系统观测向量

Wk——n维系统过程噪声

Vk+1——k+1时刻n维系统观测噪声

本文复合导引系统属于非线性系统，误差应在一定范围内，故首先使用无迹卡尔曼滤波(Unscented Kalman filter, UKF)来融合多传感器信息。标准UKF算法的流程[17]如下：

(1)选取k=0时的滤波初值来初始化。状态向量的初始协方差P0和先验均值0为

(6)

(2)计算UT变换Sigma采样点和其对应的权重系数

(7)

式中n——状态向量的维数

ξi,k——Sigma采样点

Pk——k时刻状态向量的协方差

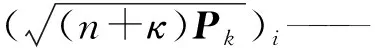
κ——第三刻度因子

(8)

(3)对Sigma点进行非线性传播，计算传播结果为

ξi,k/k-1=f(ξi,k-1) (i=0,1,…,2n)

(9)

当时间为k时，基于Sigma采样点的一步预测矩阵和协方差矩阵为

(10)

(4)进行观测更新

(11)

(12)

式中Qk、Rk——不相关零均值白噪声序列Wk和Vk的协方差矩阵

(5)根据Zk进行滤波更新。计算最佳滤波增益

(13)

更新系统状态向量和方差的预测值

k=k/k-1+Kk(Zk-k/k-1)

(14)

(15)

UKF算法通过对概率密度的近似来处理非线性问题，对系统噪声的统计信息准确性要求较高[18]。如果系统模型或者噪声统计特性存在偏差，则可能使系统估计的方差偏大，导致滤波发散。跟随AGV在任务执行过程中，可能面临较为复杂的工况环境，难以获得准确的噪声统计特性，影响最终的滤波效果。

针对上述问题，基于自适应滤波原理，提出一种自适应无迹卡尔曼滤波(Adaptive unscented Kalman filter, AUKF)算法，在UKF算法的基础上加入Sage-Husa噪声估计器[19]，通过实时调整系统量测噪声，提高UKF算法的环境适应能力。具体实现步骤如下：

(1)计算运动噪声均值

E(k+1)=(1-dk+1)k+1+

(16)

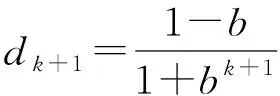
(17)

式中b——遗忘因子，通常取[0.950,0.995]

f(ξi,k,uk)——Sigma点ξi,k沿非线性函数f的传播结果

(2)计算运动噪声的协方差矩阵

(18)

式中ek+1——观测值的残差，满足ek=Zk-k

(3)计算观测噪声均值

k+1=E(k+1)=

(19)

(4)求解观测噪声的协方差矩阵

(20)

AUKF滤波流程如图10所示，对于k时刻的系统噪声特性估计值{k,k,k,k}，计算得到k时刻下的系统状态误差的协方差和估计值。将得到的结果和前一时刻过程噪声特性的估计值，通过式(16)～(20)，对k时刻噪声统计特性进行递推估计。最后更新k并重复该过程。

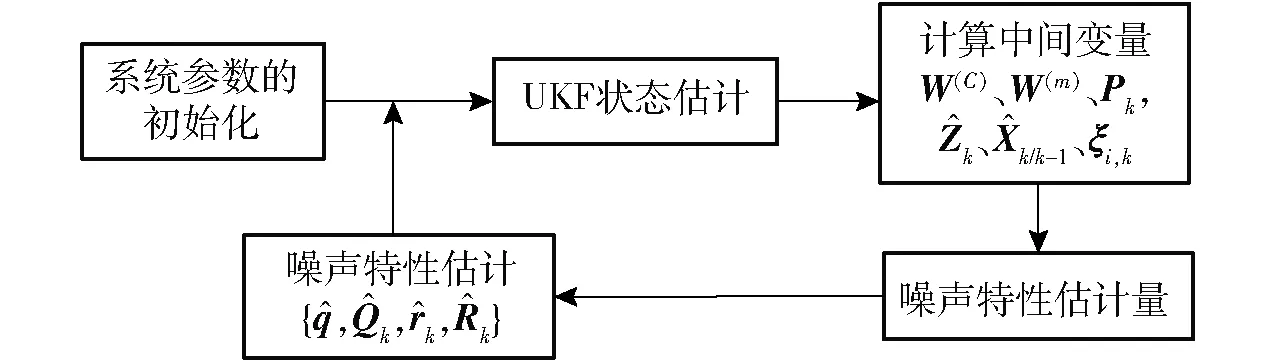
图10 AUKF算法流程图Fig.10 AUKF algorithm process chart

3.2 跟随AGV最优位姿估计方法

使用AUKF算法对双车协同系统中跟随AGV进行最优位姿估计，位姿计算流程如图11所示。AGV车载视觉系统得到的环境视觉观测，作为系统观测量；IMU传感器观测值结合运动学模型作为预测量，推导AGV运行时的位姿状态递推方程，建立预测、观测反馈闭环的最优位姿估计系统。将最优位姿估计作为导引参数输入运动控制系统，实现对跟随AGV的实时鲁棒导航。

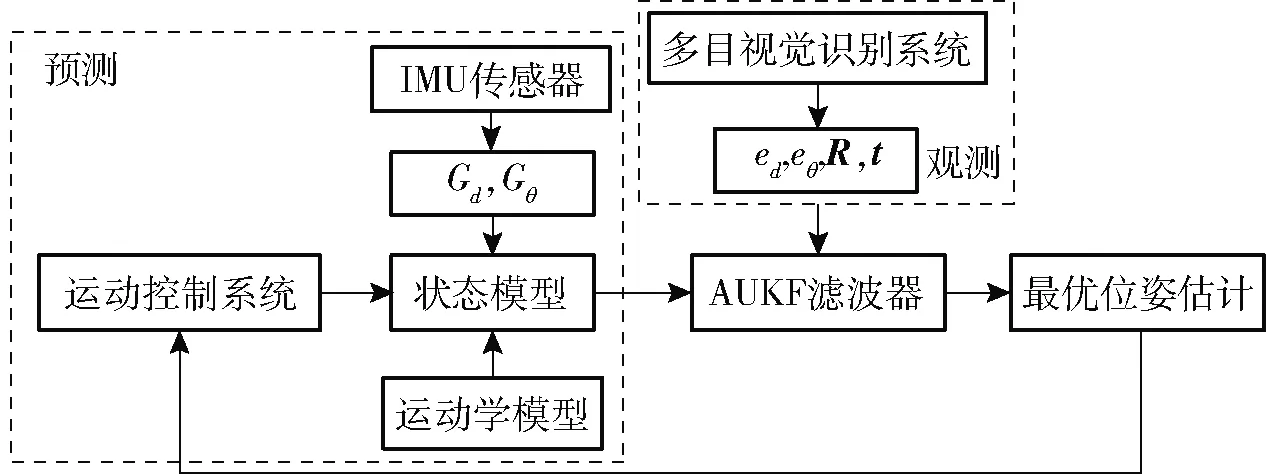
图11 基于AUKF融合算法的AGV最优位姿估计Fig.11 Optimal pose estimation of AGV based on AUKF fusion algorithm

3.2.1跟随AGV运动学模型

以麦克纳姆轮全向移动AGV作为研究对象，角度偏差eθ和距离偏差ed用于描述小车的运动状态，通过分析单个麦克纳姆轮及整车运动得到全向AGV的运动学方程。由vx、vy、ωz这3个独立的运动学参数可以实现AGV的位姿纠偏，即

(21)

式中ω1、ω2、ω3、ω4——麦克纳姆轮旋转角速度

L——1/2车长

W——1/2车宽

R——麦克纳姆轮半径

设全向AGV的控制周期为Ts，某一时刻k全向AGV相对于预设路径的角度偏差和距离偏差分别为eθ(k)和ed(k)。通过运动学以及路径运动偏差分析，得到基于路径跟踪的双车协同搬运系统的运动学模型[20]：

对于领航AGV有

(22)

对于跟随AGV有

(23)

式中vx1、vx2——领航AGV、跟随AGV速度在x方向的分量

vy1——领航AGV速度在y方向上的分量

ΔL(k)——k时刻两车实际中心距与期望距离的差值

3.2.2复合导航系统状态方程

根据惯导传感器原理，结合车辆运行状态建立状态方程

(24)

式中Gd——加速度计计算得到的位移

ΔGd——递推得到的位移增量

Gα——横向加速度

Gθ——陀螺仪计算出的AGV姿态角

ΔGθ——递推得到的角度增量

Gω——陀螺仪当前角速度

根据RGB-D视觉导航原理以及针孔相机模型，建立深度相机系统状态变量R、t的状态方程。由文献[21]可知，RGB-D深度相机的运动过程，由一个运动方程和一个观测方程构成，观测方程即针孔相机模型

(25)

式中xk——深度相机当前时刻的位姿，可以用李代数表示

yj——标识点位置

zk,j——标识点在图像中的像素位置

wk——系统过程噪声

vk,j——系统观测噪声

将式(25)转换为具体参数化形式。对于位姿xk，相机外参数R、t可以用Tk或者exp(k)来表示。假设在xk处对标识点yj进行一次预测，映射到图像中的像素位置zk,j，其观测方程可以描述为

szk,j=Kexp()yj

(26)

式中K——相机内参数

s——像素点深度信息

将yj用齐次坐标描述为

(27)

3.2.3基于AUKF的跟随AGV最优位姿估计

结合前文跟随AGV的运动学模型以及传感器的状态方程，可以得到系统状态变量的状态空间模型。由于复杂外部环境的影响，AGV在运动过程中存在噪声干扰，即过程噪声wk，在模型中以三维齐次坐标形式描述，满足均值为零的高斯分布wk～N(0,Qk)。惯导短时精度高，本文将惯导传感器的输出信号用于跟随AGV的姿态预测，系统状态预测方程用齐次坐标的矩阵形式描述为

(28)

视觉系统不存在累计误差，故将其作为观测修正惯导传感器产生的累积误差。AGV路径跟踪导航系统采集的跟随AGV与导引路径中心线的偏差ed、eθ，以及RGB-D导航系统观测的位姿信息R、t，作为观测量，构建系统状态观测方程。观测过程同样存在噪声干扰，即观测噪声vk，满足均值为零的高斯分布vk～N(0,Rk)。用齐次坐标描述为

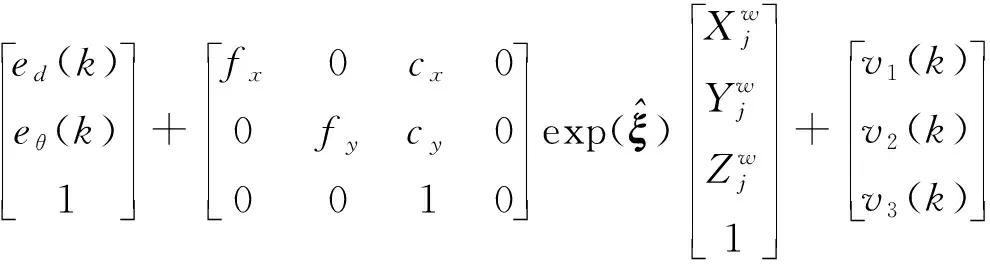
(29)

其中，ed(k)和eθ(k)的展开式为式(23)。系统过程噪声wk和系统观测噪声vk二者线性无关，且均满足均值为零的高斯分布wk,vk～N(0,Rk)，其统计特性关系满足等式

(30)

其中

(31)

式中δkj——Kronecker-δ函数

4 实验与结果分析

4.1 AUKF仿真实验

针对3.2节中提出的跟随AGV最优位姿估计方法进行仿真实验。本文实验使用的全向移动AGV驱动轮轴向间距(1/2车长)L=0.5 m，设置车速v=0.5 m/s，CCD相机采样频率H1=25帧/s，RealSense D435i型深度相机采样频率H2=30帧/s，惯导传感器采样频率H3=50帧/s。AUKF滤波采样周期Ts=0.04 s。

仿真初始状态变量设置为ed(0)=0.6 mm和eθ(0)=0.2°。AUKF算法参数设置：κ=0.1，α=0.01，β=2；同时设定初始状态噪声Q(0)=diag([0.1,0.02,0.005])，初始观测噪声R(0)=diag([0.05,0.1,0.01])。

图12和图13分别为距离偏差ed和角度偏差eθ的滤波仿真曲线。在复杂环境中，距离偏差最大值为16 mm，角度偏差最大值为13°。经过AUKF滤波后，距离偏差和角度偏差明显降低，变化曲线趋于平稳。AUKF滤波后偏差的均值和方差均小于UKF。相比于UKF算法，本文AUKF滤波算法对于复杂环境有更好的适应能力。

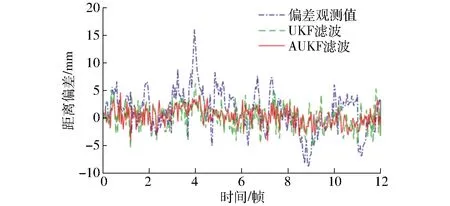
图12 ed滤波曲线Fig.12 Filtering curves of ed

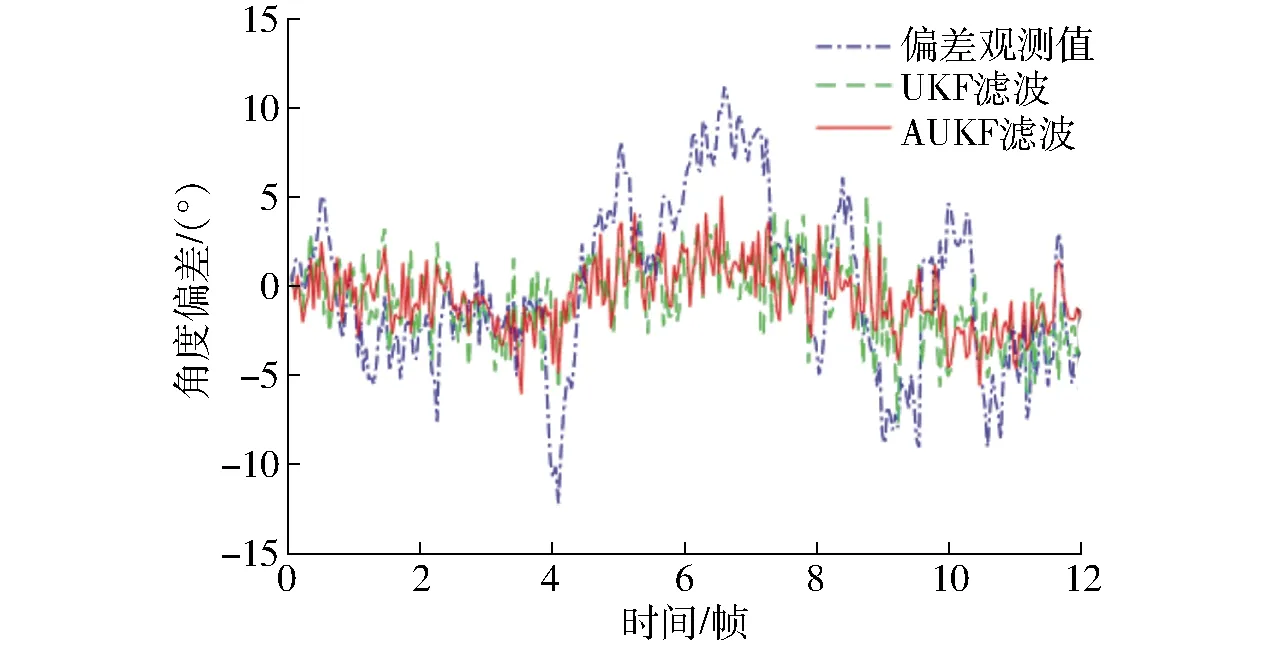
图13 eθ滤波曲线Fig.13 Filtering curves of eθ

由仿真结果可知，本文基于AUKF算法的跟随AGV最优位姿估计方法具有良好的性能，能够在一定程度上抑制复杂环境的干扰，该方法适用于跟随AGV的多传感器信息融合。

4.2 双车协同搬运实验

为了验证前述复合导引方案以及数据融合算法的整体有效性，进行双车协同搬运的对比实验验证。实验环境整体布局如图14所示，实验平台为2台麦克纳姆轮全向移动AGV组成的双车协同搬运系统。如图15所示，领航AGV在前，跟随AGV在后，共同完成较长物件的搬运任务。运行过程中，跟随AGV在导引线划定的区域范围内运行，两侧的CCD相机通过实时采集导引路径图像，防止AGV出界。跟随AGV车头安装RGB-D相机观测领航AGV，用于获取相对前车的位姿信息。

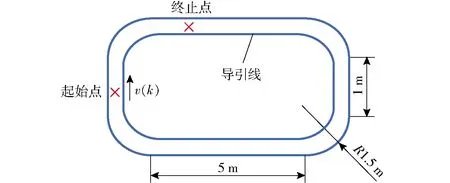
图14 实验环境布局图Fig.14 Layout of experimental environment

图15 双车协同搬运实物Fig.15 Two AGVs cooperative handling

设置AGV初始状态及状态变量如下：跟随AGV初始距离偏差ed(0)=-20 mm，初始角度偏差eθ(0)=-4°。领航AGV和跟随AGV的初始运行速度为0.4 m/s，两车初始距离误差ΔL(0)=50 mm。在k=0时刻同时启动领航AGV和跟随AGV，在执行双车搬运任务的同时，通过跟随AGV车载装配平台上的角度传感器和直线距离传感器实时采集两车间的距离偏差和角度偏差。设置一组对照组，将本文提出的整套复合导引方案与仅使用单一路径跟踪导航进行导引性能的对比，并截取中间一段具有代表性的路径偏差数据进行分析。

图16为跟随AGV运行时距离偏差ed和角度偏差eθ的变化曲线。其中，在0～4 s时间段内跟随AGV在直线路段上运行，第5秒开始进入圆弧段，第20秒驶出圆弧段回到直线路段。对于初始偏差，图16a中实线在1 s内下降到-3 mm左右，相比虚线收敛速度更快，说明本文复合导引纠偏更及时。直线路段实线的距离偏差稳定在10 mm以内，圆弧路段距离偏差在15 mm内，距离偏差均值较小。图16b中实线的角度偏差始终小于虚线，其中直线路段角度偏差最大为8°，圆弧路段最大为19°，偏差变化过程较为平滑。说明本文复合导引方案在圆弧路段运行较为平稳，未出现位姿突变。

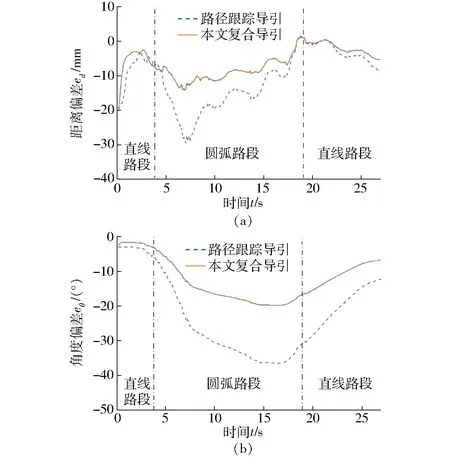
图16 跟随AGV距离偏差和角度偏差变化曲线Fig.16 Distance deviation and angle deviation of following AGV

图17为运行过程中前后两车距离偏差ΔL的变化曲线。实线在2 s内收敛至0 mm左右，后续距离偏差保持在5 mm内；而虚线收敛速度慢，且上下波动相对较大。由图17可知，在双车队形保持方面，本文复合导引方案的性能同样优于单一的路径跟踪导航。

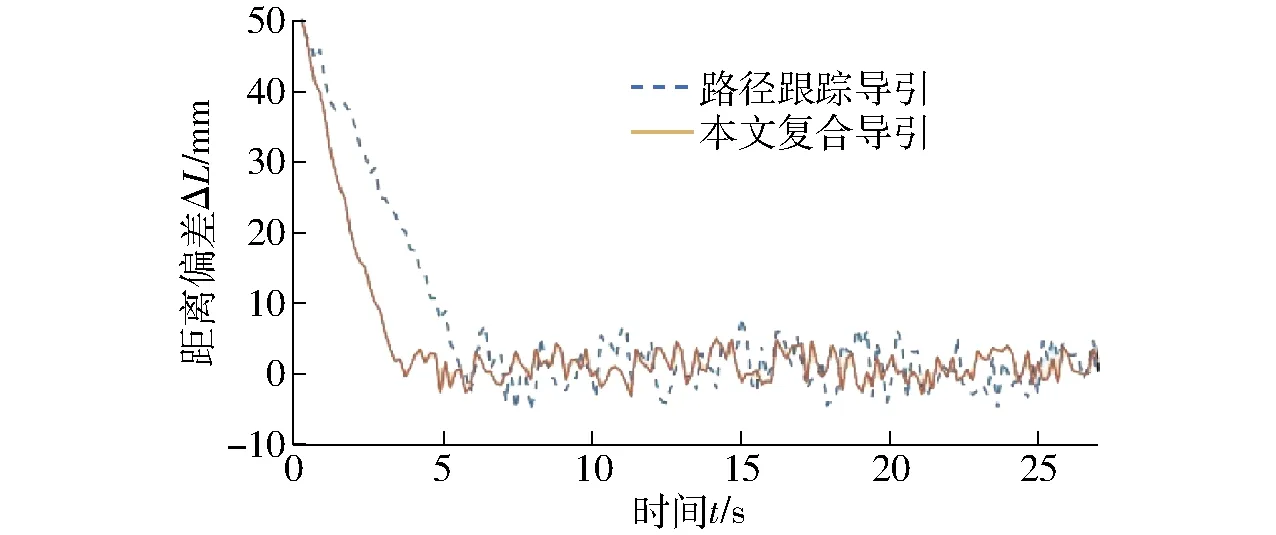
图17 双车距离偏差变化曲线Fig.17 Variation of distance deviation between two AGVs

实验结果表明，本文提出的复合导航方案具有更快的偏差收敛速度、更稳定的路径跟踪状态和队形保持。实验证明该复合导航方案具有良好的导引精度，能够提高本文双车协同搬运系统的实时性和鲁棒性。

5 结束语

针对Leader-Follower编队策略下的多AGV协同搬运，研究了面向跟随AGV定位和导引的惯导/视觉组合导航方法；对于多目视觉系统和惯性导引的数据融合问题，提出了一种最优位姿估计方法，将惯导观测数据、路径跟踪误差以及RGB-D位姿观测作为联合观测数据，与跟随AGV的运动模型结合，进行多传感器的数据融合。实验表明本文提出的复合导引方案具有良好的导引精度，能够适应双车协同搬运系统实时性、准确性和鲁棒性的要求。