基于SRTM的地形因子提取方法研究
2022-02-21张宏鸣杨勤科许伊昆
张宏鸣 常 毅 杨勤科 张 泉 董 良 许伊昆
(1.西北农林科技大学信息工程学院, 陕西杨凌 712100; 2.西北大学城市与环境学院, 西安 710069)
0 引言
地形是土壤侵蚀和水土保持措施布设的主要影响因素。在通用土壤流失方程及其修订版(Universal soil loss equation/revised universal soil loss equation,USLE/REUSLE)[1-2]和中国土壤流失方程(Chinese soil loss equation,CSLE)[3]中,地形(LS)因子是定量计算土壤流失的重要指标。区域尺度上,通常使用数字高程模型(Digital elevation model,DEM)进行地形因子提取[4]。随着无人机技术、航空摄影测量技术、激光雷达技术的发展,高精度、大范围DEM获取逐渐容易[5],如何在大区域上使用高精度DEM进行地形因子提取成为研究重点。
SRTM(Shuttle radar topography mission)是美国太空总署和国防部国家测绘局以及德国和意大利航天机构共同合作完成的地球表面遥感测量结果[6]。该数据凭借在全球尺度上精度高、范围大等优势[7],可为大区域甚至全球范围地形因子提取提供数据基础[8]。SRTM处于地理坐标系,而已有的LS因子提取方法通常基于投影坐标系,通过提取坡度、坡长,获取LS因子[9]。现阶段,坡度提取算法较多,如最陡坡降、三阶反距离平方权、三阶不带权差分等,获取较容易;坡长由于计算原理复杂,需要考虑截断等多种复杂因素,获取较困难[10]。文献[11-16]通过汇水面积法替换或径流线换算的方法代替坡长求得LS因子,但这些方法无法考虑截断问题,也不能获得坡长。文献[17-19]从坡长基本定义出发,考虑坡长的起点和终点,获取精确的坡长,根据坡长和坡度计算LS因子。文献[20-21]研究了坡度截断和沟道截断对侵蚀坡长提取的影响,可进一步提高坡长精度。文献[22-23]表明,使用分段坡长法提取到的地形因子准确性及空间分布更加合理。前人对地形因子提取的相关机理作了大量研究,投影坐标系下地形因子提取方法较为成熟。但在实际应用时,要求栅格单元以米为单位,且边长一致,无法直接对SRTM进行计算。通常需对SRTM进行坐标转换后方可应用,计算效率低,不利于大区域地形因子快速提取。文献[24]通过分析地理坐标系特点,构建地球球体模型,提出SRTM的坡度和坡向算法,但未对坡长与LS提取方法进行研究与应用。
基于此,本文提出一种基于SRTM的LS因子提取算法(LSA-SRTM)。通过模拟地球球体模型,构建换算关系及解算方法,直接在地理坐标系下提取SRTM栅格单元边长、获取坡度与流向、提取坡长,进而提取LS因子。
1 研究数据和方法
1.1 实验数据
为了验证算法的精度,需使用不同地貌类型的高程数据进行评估[16]。但实际地形的微观特征过多,数据本身存在一定的随机噪声[25],文献[26]尝试构建数学理论曲面代替实际地形,并在曲面上考虑实际地形可能存在的基本地貌类型。由于数学曲面噪声、误差等影响较小,文献[16,27]基于数学曲面进行了流向算法分析以及改进方法研究。Himmelblau-Orlandini数学曲面是文献[28]利用Himmelblau函数,通过仿射变换后生成的离散曲面,是一种复杂数学曲面,兼具凹凸面、发散汇集等特征,曲面上同时有山顶、鞍部、谷底等地形特征,与实际地形条件吻合,且通过其生成模型,可计算理论真值,方便进行误差、精度检验,同时可以避免投影转换的误差,减少误差的累积效应。
Himmelblau-Orlandini曲面的原始函数为
Z(X,Y)=(X2+Y-4)2+(Y2+X-7)2
(-5≤X≤5;-5≤Y≤5)
(1)
为了方便该曲面进行DEM离散表达,使用
x=50X+250
(2)
y=50Y+250
(3)
z=-0.75Z+450
(4)
式中x——x轴坐标值,取0~500 m
y——y轴坐标值,取0~500 m
z——(x,y)的高程
对曲面进行仿射变换[28],生成0~500 m尺度的SRTM如图1所示。
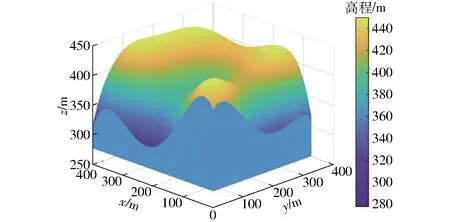
图1 数学曲面Fig.1 Mathematical surface
1″(分辨率约30 m)SRTM(来源:https:∥e4ftl01.cr.usgs.gov/)为HGT格式,采用WGS 1984坐标系。整套数据覆盖60°N~56°S,总面积超过1.19×108km2,单个数据文件覆盖1°(经度)×1°(纬度)的地区。目前,基于该数据的地形因子结果分析已有大量研究。文献[29]的研究表明,DEM格网扩张会降低LS的提取精度,1″ SRTM的LS因子计算精度高于3″ SRTM。文献[30]的研究表明,在特定的海拔范围,1″ SRTM提取的地形因子甚至优于10 m分辨率的DEM。文献[31]的研究表明1″ SRTM稍差于25 m的Hc-DEM(水文地貌关系正确的DEM),但比相同分辨率的ASTER GDEM(先进星载热发射和反射幅射仪全球数字高程模型)地形表达能力更好。文献[32]对1″ SRTM的侵蚀表达能力作了分析,认为研究样区较大、缺少连续的高精度DEM时,1″ SRTM可以代替使用。因此,目前全球尺度的土壤侵蚀多基于此数据进行[8]。
选取全国土壤侵蚀强烈、侵蚀地貌发育的5个典型样区为实验区(图2)。包括:东北漫岗丘陵区(黑龙江省齐齐哈尔市拜泉县),代表波状起伏的缓坡丘陵;黄土丘陵区(陕西省延安市安塞县),代表半表深厚黄土覆盖、强烈水蚀作用的陡坡丘陵;西南紫色土丘陵区(四川省绵阳市盐亭县)与南方红壤丘陵区(浙江省金华市东阳县),代表亚热带湿润多雨环境下的丘陵;北方土石山区(山东省临沂市蒙阴县),代表暖温带半湿润、半干旱环境下的山地地形景观[33]。各个样区尺寸均为1°×1°,样区高程数据如图3所示。
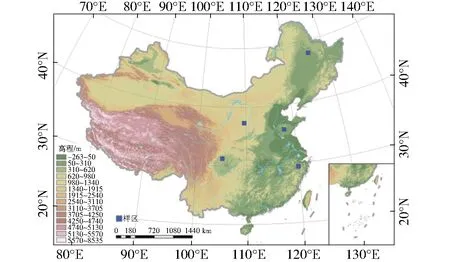
图2 样区分布图Fig.2 Location of samples

图3 典型样区数字高程模型Fig.3 DEM samples
1.2 实验方法
LSA-SRTM的核心过程主要分为5个步骤,算法流程如图4所示:利用经纬度信息计算栅格的单元边长及单元坡长;利用Deterministic 8(D8)算法计算流向和坡度;依据坡度和截断因子设置坡度截断点,根据汇水面积和指定的阈值设置沟道截断点;参考截断位置,计算累积坡长;根据CSLE,利用坡度和累积坡长计算LS因子。输入的SRTM数据是ASCII数据,在计算前对输入数据的合法性进行判断。

图4 基于SRTM的地形因子提取流程图Fig.4 Flow chart of topographic factor extraction based on SRTM
1.2.1SRTM单元边长计算
SRTM基于地理坐标系,栅格以弧度作为基本单位存储,与投影坐标系统下的DEM栅格不同,每个栅格单元近似看作梯形,相邻单元之间的距离只能通过地球半径和经纬度进行计算。

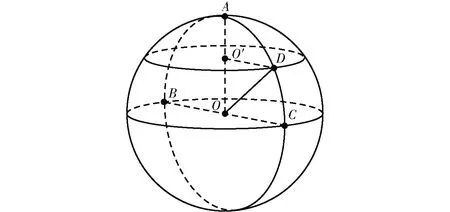
图5 地球球体模型Fig.5 Earth sphere model
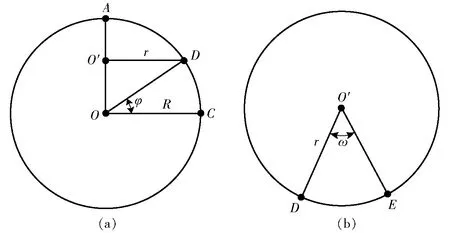
图6 地球经线面和纬线面示意图Fig.6 Schematics of longitude and latitude planes of earth
(5)
(6)


由r=Rcosφ有
(7)
由于SRTM单元在经纬度上的跨度相同,以1″SRTM为例,其跨度为0.000 277 777 777 778°。取地球半径R=6 371 000 m,ω=1(°)/3 600,SRTM栅格单元宽度在南北方向恒定为30.887 479 1 m,在东西方向随纬度变化。
1.2.2坡度和流向提取
坡度和流向采用D8算法[34]计算。D8算法基于最陡坡降思想,在3×3的DEM网格上,计算中心单元格与各相邻单元格间的坡度,取坡度结果最大值作为中心单元格的坡度,并且将最大值所在方向确定为中心单元格的流向[35]。如图7所示,C为当前单元所在的位置,其流出方向为周围8个单元中的一个,分别标记为1、2、4、8、16、32、64、128[11]。为确保每个栅格单元都与河网连接,当单元格坡度为0时,取0.1[10]。

NW32N64NE128W16CE1SW8S4SE2
1.2.3坡长提取
坡长是从起点沿着垂直等高线方向到达坡长截断终点的积分,基于栅格数据进行计算时,坡长的解算主要由每一个栅格的单元坡长累积来计算完成[10]。其公式可表示为
(8)
式中λi,j——坐标点(i,j)的坡长
λc——每个栅格的单元坡长
m——坡长指数
k——汇入坐标点(x,y)的栅格数
本研究考虑截断对坡长的影响,坡度截断通过判断坡度变化率和中断因子的关系来确定,当坡度变化率大于中断因子时,该点标记为截断点[21]。沟道截断通过设置阈值的方法确定,当汇水面积大于阈值时,标记该点为截断点[20]。本文将汇水面积阈值设置为105m2。
累积坡长的计算方法是以起点栅格为基础,沿周围8个不同方向的最大坡降方向累加坡长。对于SRTM数据,无法确定某条流路方向的最大坡长,因此,需对栅格点正向、反向遍历,从栅格数据起点逐点计算来完成累计坡长计算[19]。
1.2.4地形因子提取
在CSLE中,坡长和坡度共同决定了侵蚀地形因子的计算[29]。为避免只考虑均匀坡长带来的误差[36],使用分段坡长因子公式来计算坡长因子。LS因子的计算公式为
(9)
(10)
其中

式中θ——坡度S——坡度因子
λin——入口坡长,m
λout——出口坡长,m
L——坡长因子
1.2.5实验对比方法
(1)精度对比
在格网DEM上,完整获取各个位置的地形因子真值非常困难,精度对比需对检验样区选定样点测量完成。参照文献[37],在实验样区中选取较为规整的坡面样点,样本空间设置为150,需避免将样点设在明确的分水线和沟谷中[38]。根据DEM绘制(等间距小于cellsize)等高线,在高程变化平缓的区域减小等高线间距,采用ArcGIS 10.2的量尺工具,量算采样栅格中心点沿与等高线垂直方向到明确分水线或山顶(水流起始点)的投影距离作为该栅格的实测坡长,取多次测量的均值作为最终结果,结果保留小数点后两位,不考虑人为误差时,有效测量精度为0.1 m。基于实测坡长计算得到的LS因子为实测LS因子。以投影坐标系下的LS算法[19](简称为LSA-DEM)作为参照方法,将两种方法的计算结果与实测结果进行对比。
确定计算精度时,使用回归分析方法以及决定系数R2,衡量计算结果与测量结果的相关性;使用标准差(SD)以及绝对差(AD)确定计算误差。
(2)效率对比
在64位Dell Precision工作站(系统:Windows 10;RAM:64 GB;CPU:Intel Xeon Gold 5115;主频:2.4 GHz)对两种方法的运算时间进行统计。样本大小分别为:500 m×500 m,1°×1°、2°×2°、5°×5°、14°×14°。为避免不可控因素对运算时间测量的干扰,对每一测试样本均进行5次运算,取其运算时间的平均值作为实际执行时间。
2 结果与讨论
2.1 数学曲面提取结果分析
数学曲面上,LSA-SRTM计算结果见图8a~8c,坡度最大值为84.97°,最小值为0.1°,平均值为50.91°(表1)。坡度高值均分布在4个局部高点外侧陡坡区域,局部高点内侧坡度变化不明显(图8a)。仅在坡度截断作用下,坡长最大值为407.65 m,最小值为0.48 m,坡长均值64.96 m。坡长从局部高点向坡度变化最陡的方向累加,在汇集坡面可累计至流域边界,能反映地表起伏状态(图8b)。LSA-DEM提取结果见图8d~8f,两种方法的纹理特征无明显差异,3种地形指标的均值与标准差十分接近。
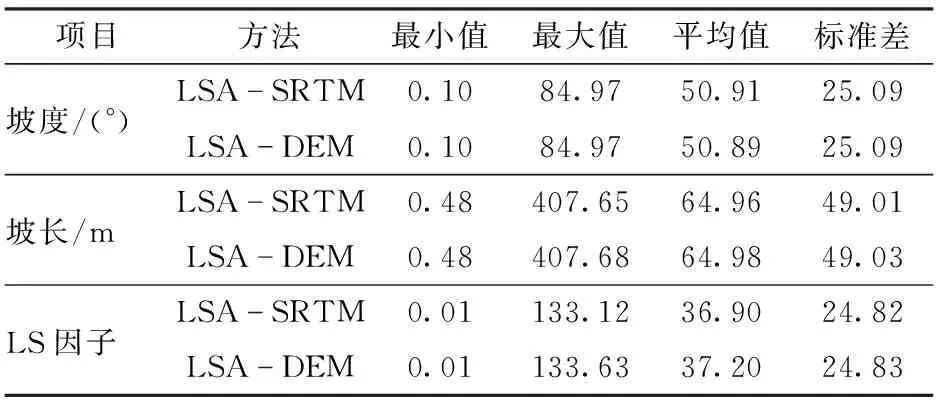
表1 数学曲面上LSA-SRTM和LSA-DEM结果Tab.1 Results of LSA-SRTM and LSA-DEM in mathematical surface

图8 数学曲面上地形因子提取结果Fig.8 Topographic factors extraction results in mathematical surface
两种方法与测量值对比如表2所示。由表2可见,两种方法的结果与测量值均呈现较强的相关性。LSA-SRTM与测量坡长的R2为0.855 2,与测量LS因子的R2为0.890 7,由此可见,计算结果与测量结果有较高的相关性,可以较好地表达真实地形。计算结果与实测坡长的SD与AD分别为26.34、18.98 m,与实测LS因子的SD与AD分别为6.41、3.94。

表2 数学曲面上LSA-SRTM和LSA-DEM结果对比Tab.2 Differences between LSA-SRTM and LSA-DEM results in mathematical surface
计算结果与实测结果有较高的一致性,误差范围较小,从回归分析的结果来看,两种方法具有高度相似的误差来源。误差的主要原因在于单流向D8方法应用的局限性,D8方法的流向只能选择周围8个栅格中的一个,这使得发散坡面上易出现栅格缺失上游水流入情况[39],影响坡长的累积结果。
2.2 典型样区提取结果分析
典型样区上3种地形指标统计结果如表3~5所示。
从表3可看出,漫岗丘陵区坡度最为平缓,平均坡度和坡度标准差均最小,坡度基本在6°以下;其次为北方土石山区,平均坡度较小,小于5°的面积占23%;整体地形由缓到陡依次为紫色土丘陵区、黄土丘陵区和红壤丘陵区;平均坡度和标准差最大的是红壤丘陵区。
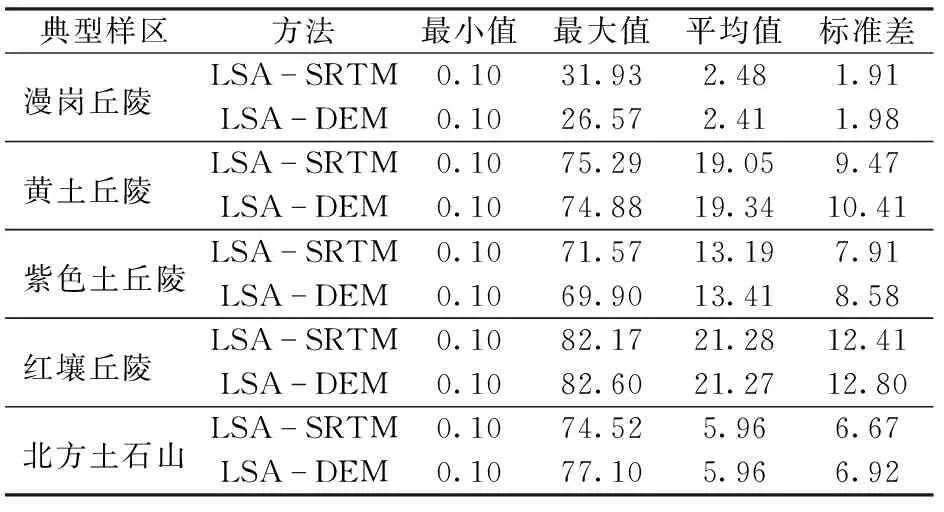
表3 典型样区LSA-SRTM与LSA-DEM坡度Tab.3 Slope gradient results of LSA-SRTM and LSA-DEM in typical samples (°)
从表4可知,平均坡长最大的是漫岗丘陵区,其次为紫色土丘陵区、红壤丘陵区、北方土石山区,黄土丘陵区的平均坡长最小,与其支离破碎的地形相适应,5个样区的坡长大多在200 m以内。

表4 典型样区LSA-SRTM与LSA-DEM的坡长Tab.4 Slope length results of LSA-SRTM and LSA-DEM in typical samples m
从表5可知,LS因子由漫岗丘陵区、北方土石山区、紫色土丘陵区、黄土丘陵区和南方红壤丘陵区依次增加。漫岗丘陵区LS因子在0.5以下的面积约75%;黄土丘陵区LS因子主要分布在5以上,其中大于20的部分占35%左右;西南紫色土丘陵区LS因子在0.5以下的部分约占5%,大于20的部分占18%左右;南方红壤丘陵区LS因子在0.5以下的面积占19%,大于20的部分占23%左右;北方土石山区LS 因子主要分布在0.5~20之间,0.5以下占11%左右。该结果与文献[31]的研究结果基本一致。

表5 典型样区LSA-SRTM与LSA-DEM的LS因素Tab.5 LS factor results between LSA-SRTM and LSA-DEM in typical samples
由于篇幅原因,本文给出黄土丘陵区的结果示意图(图9)。从宏观角度观测,两种算法得到的3

图9 黄土丘陵区地形因子提取结果Fig.9 Extraction results of topographic factors in loess hilly
种地形指标的空间格局和纹理分布十分接近。
典型样区上两种方法与测量值的对比结果见表6。由表6可见,5个样区上LSA-SRTM与坡长测量值的R2分别为:0.778 8、0.726 9、0.702 4、0.690 9、0.725 5;对应的SD分别为:46.12、57.38、43.66、44.63、39.41 m;AD分别为:32.16、38.20、31.19、26.69、19.75 m。与LS因子测量值的R2分别为:0.820 9、0.821 3、0.714 2、0.714 5、0.821 2;对应的SD分别为:7.97、8.83、8.54、7.69、6.52;AD分别为:5.14、7.63、6.13、4.79、3.56。两种方法与测量值的相关性接近,从计算误差上看,LSA-DEM的SD与AD指标均高于LSA-SRTM。主要原因是投影转换导致高程在转换前后发生改变、栅格点位偏移,对后续计算引起连锁反应。相较于数学曲面的结果,典型样区上,坡长与LS的精度都有所下降,主要与实验数据的分辨率下降有关。

表6 典型样区上LSA-SRTM和LSA-DEM结果对比Tab.6 Differences between LSA-SRTM and LSA-DEM results in typical samples
2.3 效率分析
LSA-SRTM与LSA-DEM的运行时间如表7所示。在500 m×500 m(数学曲面)的样本上,由于两种方法计算的栅格数一样,且不需要投影转换时,LSA-DEM与LSA-SRTM的运行时间持平。在1″SRTM上,LSA-DEM的运算时间更长,主要与投影变换的时间开销,以及变换引起的输入计算的栅格数增多有关。LSA-SRTM可以有效节省坐标转换时间,计算效率更高。
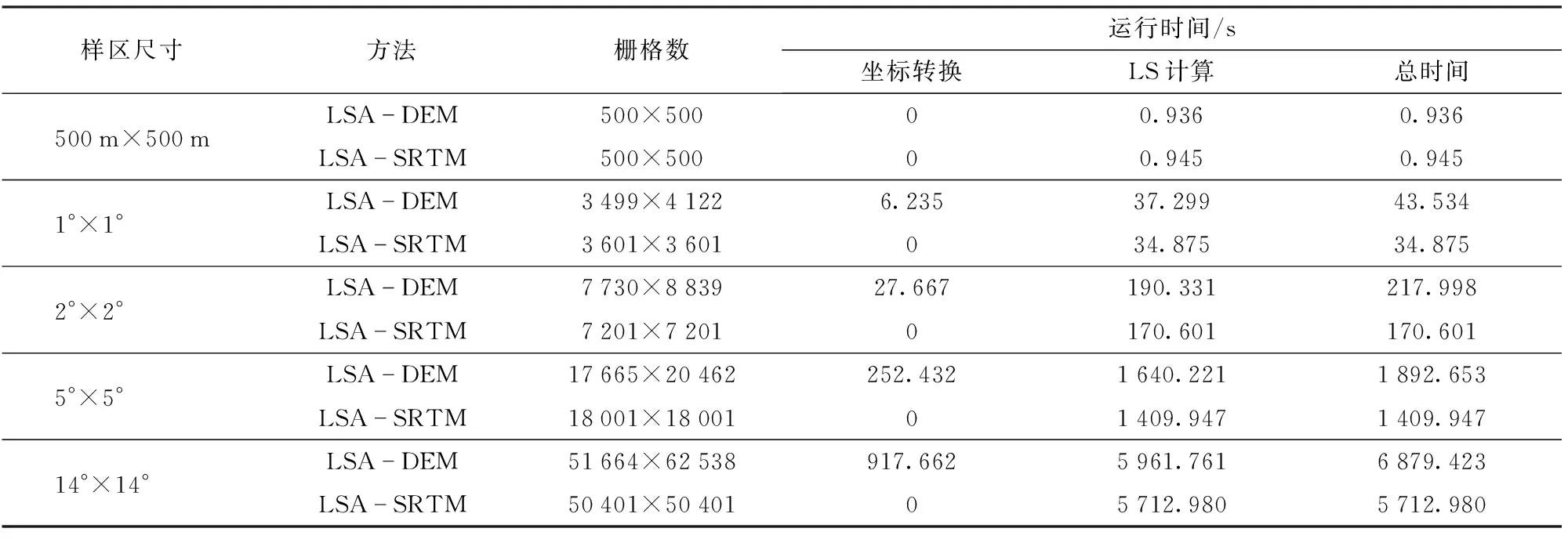
表7 LSA-SRTM与LSA-DEM运行时间Tab.7 Running time of LSA-SRTM and LSA-DEM
3 结束语
针对传统LS方法计算SRTM需投影转换、效率低的问题,本文提出了一种基于SRTM的地形因子提取算法(LSA-SRTM)。并对该算法的精度和效率与投影坐标系下的LS提取算法(LSA-DEM)进行对比分析。通过实验验证得出,在5个典型样区上,LSA-SRTM的LS结果与实测LS的R2分别为:0.820 9、0.821 3、0.714 2、0.714 5、0.821 2,精度高于LS-ADEM;SD分别为:7.97、8.83、8.54、7.69、6.52,误差小于LSA-DEM。同时,LSA-SRTM保持计算前后栅格的规模、节省投影转换的时间开销,当栅格尺寸为50 401×50 401时,计算时间比LSA-DEM少约1 166.443 s,提高了地形因子提取效率。本文方法在保证计算精度的同时,提高了地形因子提取效率,可为大区域上地形因子研究提供支撑。
