履带式农机设计及其爬坡运动学仿真

青宗翼，黄 龙，樊 越，任振兴

(成都大学 机械工程学院，成都 610106)

0 引言

作为农业大国的中国存在多种地形的农业耕地环境，适合北方平原地区的农业机械难以适应多丘陵地形特点的四川地区。随着农业设备机械化和自动化的飞速发展，履带车辆在农业生产中应用越来越广泛[1-2]。相比于轮式车辆，履带车辆在农业生产工作以及道路行驶稳定性方面有着明显优势[2]。近年来，国内外学者对履带车辆进行大量仿真分析及试验研究[3-8]。履带行走装置作为农机的运行部分，也是整台农机的支承基座，承受农机的自重及工作装置工作时的阻力，关系到整机的工作性能。在履带农机设计过程中，必须合理设计行走装置。本文基于动力学软件RecurDyn/Track(LM)，构建履带式农机履带行走机构的三维模型，采用动力分析方法对履带式农机的坡道行驶稳定性进行了仿真分析，以期为履带农机行驶稳定性提供参考。

1 农机爬坡稳定性分析

爬坡稳定性是指农机爬坡过程中受到各种外部干扰而不改变前进方向，并维持稳定爬坡的能力。为了便于建模计算，本文主要针对农机在坡道状态下的匀速行驶或制动时不产生倾翻或滑移展开分析。根据坡道行驶方向，可分为纵向稳定性和侧向稳定性，本领域一般采用倾翻角和滑移角作为爬坡稳定性的评价标准。在分析过程中，做如下假设：坡道仅仅只有一个方向的倾斜角度，纵向坡道或横向坡道，所谓的纵向坡道是指农机沿坡度方向行驶，横向坡道是指农机在坡道的等高线上行驶；农机的履带轨距相等，坡面无凹凸状。农机在坡道上稳定行驶时所受的作用力主要包括农机自身重力、前进方向的空气阻力、支撑地面的法向反力、行驶时的地面摩擦阻力以及农机自身的牵引力。

1.1 纵向行驶稳定性

纵向行驶稳定性是指农机沿坡道坡度方向行驶时农机整体以履带前后支重轮为中心分别翻转的可能性，在此，可以采用纵向极限翻倾角βlim和纵向滑移角βφ作为纵向行驶稳定性的评价指标。

1)匀速上坡行驶时，履带式农机在纵向坡道上行驶时的受力分析如图1所示，其中匀速上坡时纵向极限倾翻角为βlim和纵向滑移角为βφ，L为履带接地长度，mm；c为农机质心与后轮间距，mm；a为农机质心与前轮间距，mm；h为农机质心与地面间距，mm；m为地面反力与后轮间距，mm；N1为地面对履带的垂直支撑力，N；F1为履带受到地面的阻力，N；G为农机自重，kg。

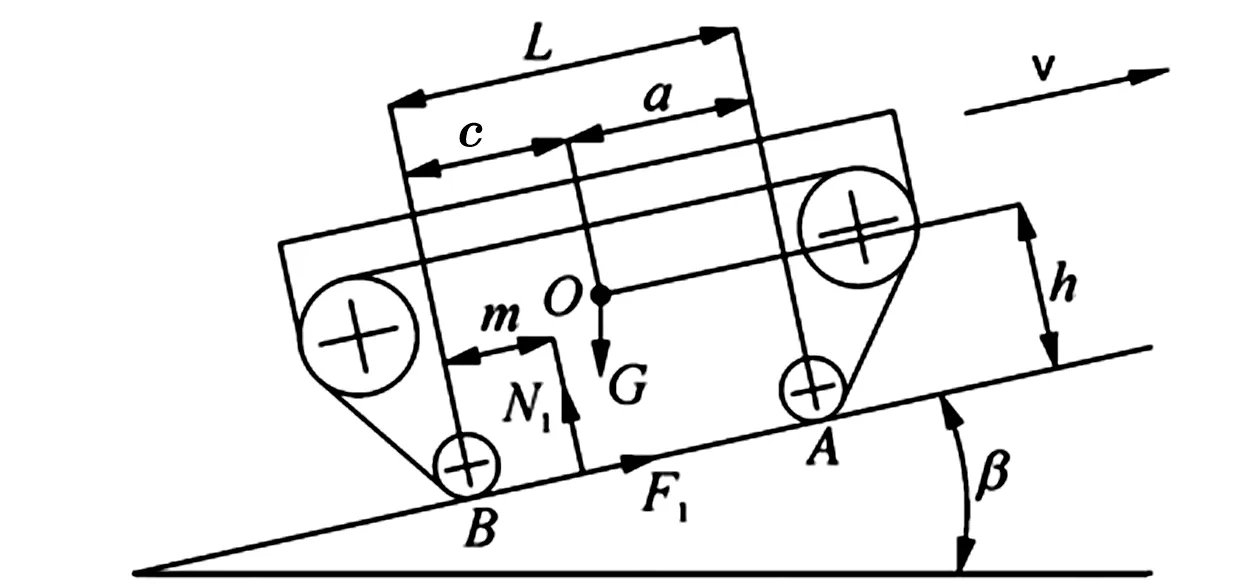
图1 履带式农机沿坡度方向爬坡匀速行驶

当履带式农机匀速在坡道上爬坡时，其所受到的外部因素较小，可假设其在坡道上处于静止状态，农机受力平衡[9]，可得平衡方程

(1)

对B点取力矩，可得力矩平衡方程bGcosβ-hGsinβ-N1m=0，对其化简可得

(2)

而要使农机在爬坡过程中不发生倾斜，需满足m≥0，即Gbcosβ-Ghsinβ≥0，求解此式，可得农机在坡道坡度方向爬坡时不发生倾翻的极限倾翻角为

(3)

坡道坡度方向爬坡的最大滑移角βφ由农机履带与地面之间的附着条件决定，可设路面与履带组件的附着系数为ξ，此时，农机在坡道上受力平衡，其平衡方程为

(4)

农机附着力为FΦ=ξN1=Gξcosβφ，其中FΦ为农机驱动机构产生得牵引力。

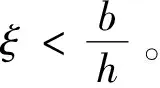
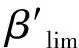
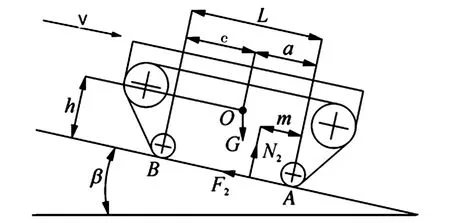
图2 履带式农机沿坡道坡度方向匀速下坡行驶

由农机平衡和力矩平衡对履带农机进行力学分析，可得

(5)

要使农机不发生倾斜，则需满足m≥0，即Gacosα-Ghsinα≥0。因此，可得到农机在坡道上行驶时不发生倾翻的极限倾翻角为

(6)

综上所述，履带式农机在坡道坡度方向匀速行驶时，其稳定行驶性能是由农机自身的结构参数和履带与土壤间的附着系数共同决定。

1.2 侧向行驶稳定性

侧向行驶稳定性是指农机沿坡道的等高线上匀速行驶时，农机整体以左右履带为支撑分别翻转或滑移的可能性，在此，可以采用侧向极限翻倾角、侧向滑移角作为侧向行驶稳定性的评价指标。农机在坡道上沿坡道等高线行驶如图3所示，其中侧向极限倾翻角为βlim和侧向滑移角为βφ。

图3 履带式农机沿坡道等高线匀速行驶

图3中，S为履带轨距,mm；b为履带宽度,mm；e为农机质心与纵向对称平面之间的距离,mm；N3和N4为地面对履带的垂直支撑力，N；F3和F4为两侧履带分别受到地面的阻力，N。

根据农机在坡道等高线上的受力平衡方程可得

(7)

对A点取力矩

N4S-Gcosβ(0.5S-e)+Ghsinβ=0

(8)

整理得

(9)

要使农机不发生侧向侧翻，需满足N4≥0，即G(0.5S-e)cosβ-Ghsinβ≥0。整理可得，农机不发生侧翻的最大侧向倾翻角为

(10)

由式(10)可知，农机侧向行驶稳定性主要与履带底盘轨距、履带宽度和农机整体质心位置有关，即履带式农机的侧向行驶稳定性与其自身结构参数有关。当履带底盘轨距一定时，最大侧向倾翻角与质心高度成反比，当质心高度一定时，最大侧向倾翻角与轨距成正比关系。

农机在坡道等高线上行驶时的最大滑移角βφ由履带与地面之间的附着条件决定。基于农机在坡道上的受力平衡，不发生侧向滑移时，应满足

F3+F4≥Gsinβ

(11)

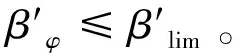
而(F3+F4)max=γGcosβ≥Gsinβ，即农机在坡道等高线上行驶时不产生侧向滑移的最大坡道角为

βφ=arctanγ

(12)

履带式机械在实际行驶过程中，均会存在切线驱动力FK。考虑到农机在坡道等高线行驶受到切线驱动力的作用，农机所受到的侧向附着力会减小，如将履带式农机看成一整体，在切线驱动力的作用下其受力平衡模型如图4所示。

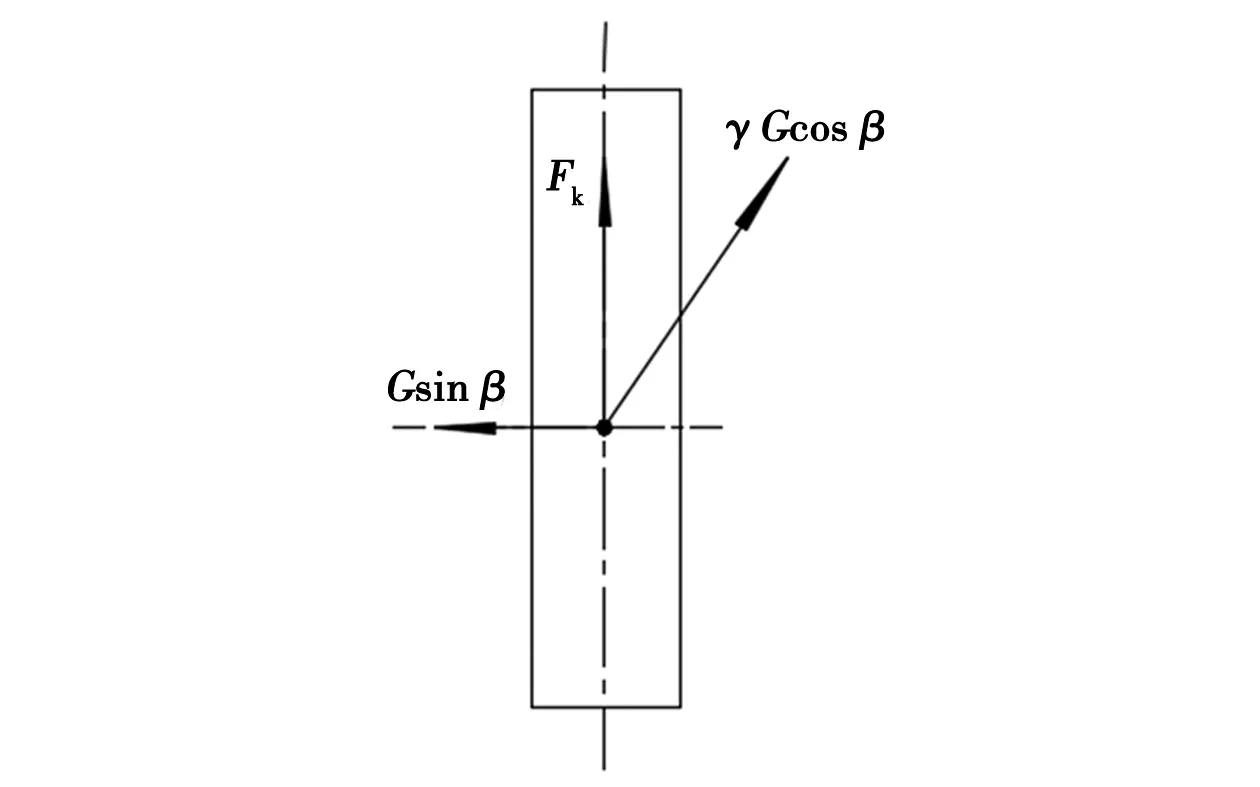
图4 切线驱动力对附着力的影响

根据图4农机滑移平衡模型，要使农机不发生侧向滑移需满足

(13)

由式(12)(13)可得，考虑切线驱动力的时候，最大侧向滑移角βφ1为

(14)

由此可知，最大侧向滑移角βφ1小于βφ，且FK越大，βφ1越小。

2 爬坡能力

履带式机械的重要优势就是爬坡能力强，可以应对各种复杂的路面状况。履带式农机为了适应丘陵山地等复杂地形，其爬坡能力尤其重要。农机在实际工况中需克服各种阻力，以便正常运行。而对于履带式农机在爬坡时所需的驱动力FK需要从两个方面考虑，一是受动力源驱动力限制，二是受履带与路面之间的附着力限制两种情况。

2.1 动力源驱动力限制的爬坡能力分析

动力源的最大驱动力为

(15)

式中p—动力源最大扭矩时的功率，kW；

η—机械传动效率，0.94～0.98，取0.96；

v—动力源最大扭矩时速度，km·h-1。

简化得到

(16)

设β=arctanf,则

(17)

2.2 履带与路面之间的附着力限制的爬坡能力分析

履带式农机在斜坡坡度方向上匀速行驶时，由受力平衡可知，其驱动力应满足为F=Gsinα，农机在坡道上最大静摩擦力系数为μ，最大静摩擦力为

FK=μmgcosα

(18)

当FFmax时，履带拖拉机将受重力影响沿斜面下滑。不同路面的最大摩擦系数μ不同，可计算出履带式农机的最大爬坡坡度为

αmax=arctanμ

(19)

履带式农机在爬坡时克服静摩擦力所需的最大加速度为

a=(μcosα-sinα)g

(20)

即，可根据履带式农机与地面的摩擦系数来确定履带拖拉机的最大爬坡能力。

3 农机基本参数

对农机的履带行走装置而言，其主要性能参数包括行驶速度、最大爬坡角度、接地比压、最大牵引力等。本项目所设计的履带式农机行走机构的基本参数如表1所示。

表1 农机基本参数

对于履带式农机的行走系统而言，首先需核算履带的平均接地比压，即履带对行驶地面的平均压强，该指标决定了履带底盘的通过性，由农机自重、履带条数、履带接地长度决定

(21)

式中p—平均接地比压，MPa；

G—农机自重与负载,kg；

n—履带条数，取n=2；

b—履带宽度,mm；

L—履带接地长度,mm。

设计履带行走系统时，在结构允许的范围内应使平均接地比压尽可能小，一般推荐平均接地比压p≤0.26MPa[10]，取p=0.068 MPa，满足要求。

4 坡地行驶仿真

4.1 几何模型的建立

在建立履带式农机的几何模型时，一般对履带行走机构做简化处理，将相应的动力源、减速器、车架、车体附加设备等简化为一刚体，此时履带式农机简化为主体和履带行走机构，采用Solidworks对主体进行建模，导入RecurDyn软件中，利用Track-LM模块建立履带行走机构[11-14]，每侧的履带行走机构均包括驱动轮、支重轮、拖链轮、张紧轮、履带和履带架。图5为履带行走机构总体模型图，在RecurDyn设置农机整机质量以及材料属性，设置履带式农机质心坐标为(-200，600，20)。

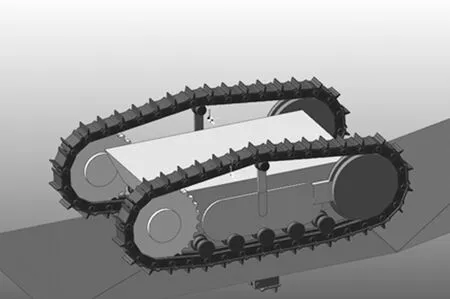
图5 履带行走机构总体模型图

4.2 添加约束

本项目所述的农机履带行走机构各零部件之间的连接关系如表2所示。分别对左右两侧履带的驱动轮添加速度驱动函数，分别为低速挡STEP(TIME,0,0,0.1,-4.78)、高速挡STEP(TIME,0,0,0.1,-34.41)。

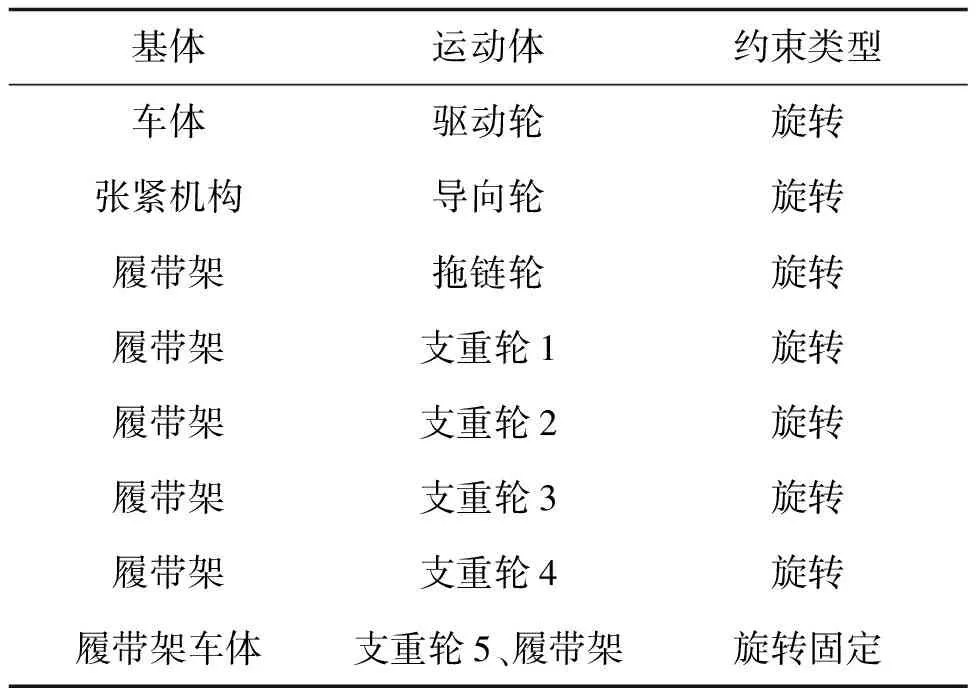
表2 履带各零部件之间的约束关系

4.3 地面模型建立

RecurDyn/Ground模块提供了相应的仿真路面模型，根据农机爬坡仿真需求添加相应路面斜坡轮廓曲面，再设置相应的路面参数。本论文中采用黏土(Clayey Soil)地面模型，其路面参数如表3所示。

表3 黏土地面模型的参数

4.4 爬坡稳定性仿真

对上述黏土土壤的不同坡度斜坡进行仿真，探讨履带式农机的最大爬坡角度。当履带式农机爬坡过程中达到最大俯仰角时，农机会发生倾翻，此时的最大坡度角即为纵向极限倾翻角。采用低速挡(1 km·h-1)进行仿真，经多次仿真得出，履带式农机在黏土路面的最大爬坡角度为25°。在黏土路面分别建立10°、15°、20°的斜坡，模型如图6所示，采用低速挡进行仿真，分别对X、Y方向的速度以及俯仰角进行分析，结果如图7所示。

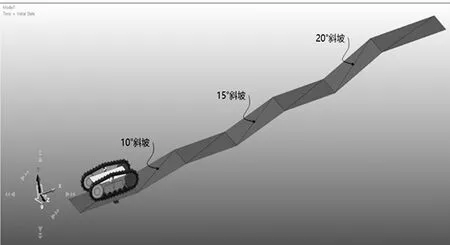
图6 黏土路面爬坡模型

履带式农机在爬坡时，俯仰角是农机能否爬坡的关键指标之一。由图7可知，仿真开始时，农机在平地加速行驶，农机俯仰角受农机启动加速度影响，在一定范围内波动；农机爬坡时，俯仰角受坡度角影响，爬坡完成后，俯仰角恢复正常，农机保持平稳行驶。同时，由图7可知，当履带式农机所爬坡的坡度越大时，农机的爬坡速度随之下降，此时，相同时间内农机的爬坡行驶距离变短，且在爬坡结束后速度变化越大，造成农机出现不稳定状态。

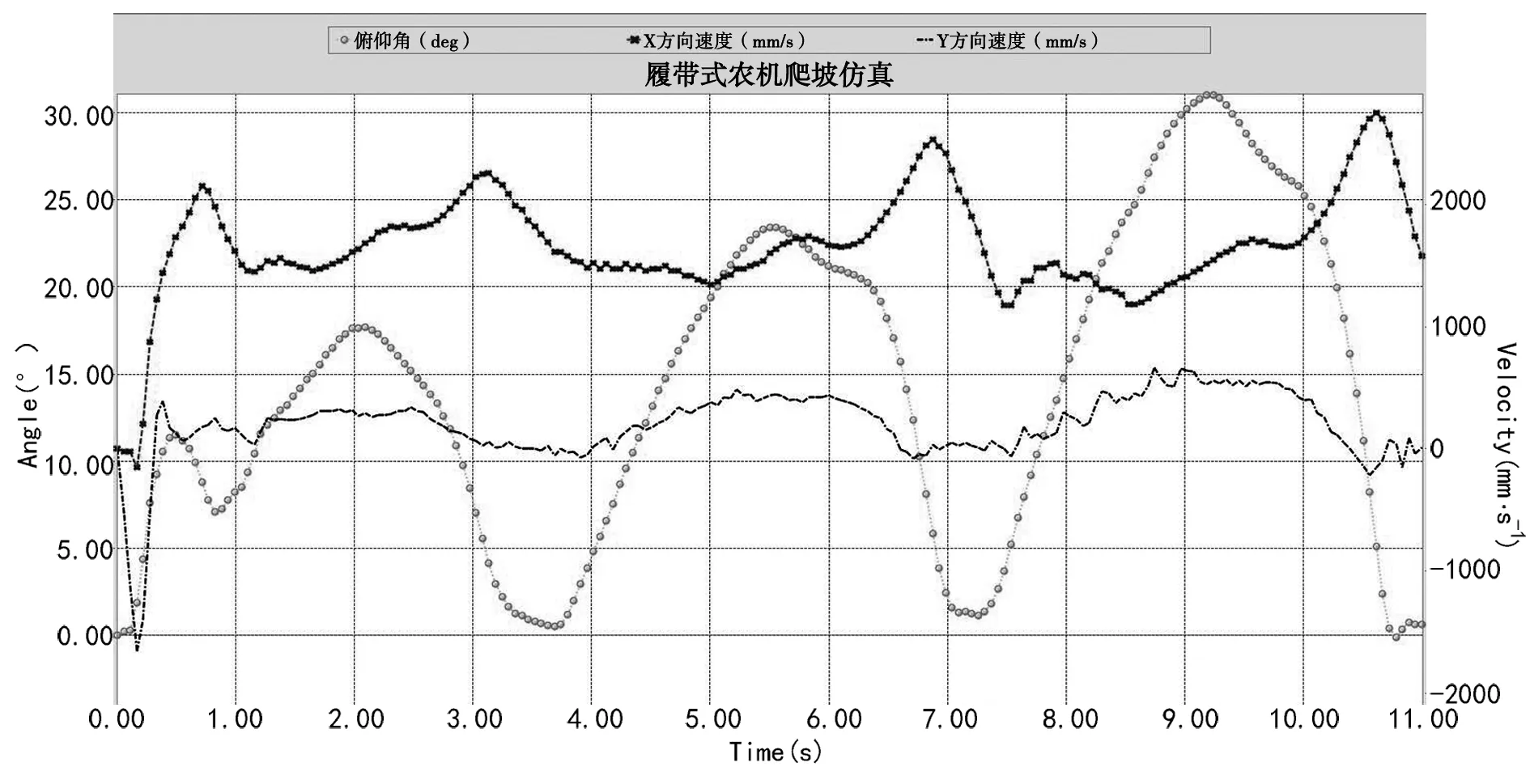
图7 履带式农机纵向爬坡行驶仿真结果曲线

5 结论

对履带式农机行驶稳定性进行了静态分析，建立了履带式农机的纵向稳定性模型和侧向稳定性模型，求得各工况下履带式农机的静态稳定条件，通过分析计算得出，行驶坡度、农机的整机参数、履带与地面的附着系数对农机的稳定性起决定性作用。采用多体动力学软件RecurDyn对履带式农机建立仿真模型，对其爬坡性能进行动力学仿真，得出该履带式农机在黏土地的纵向最大爬坡角度为25°，满足四川丘陵地区的广泛使用。