考虑运费共担的三级时滞变质品供应链定价与协调
2022-02-19张云丰龚本刚
张云丰,龚本刚,王 勇
(1.安徽工程大学 经济与管理学院,安徽 芜湖 241000;2.重庆大学 经济与工商管理学院,重庆 400030)
0 引言
易变质品是指存储过程中会发生腐烂、干燥、气化、挥发、衰减、蒸发等物理化学现象而致使利用价值降低的一类物品,如水果、蔬菜、药品、时尚服装、电子产品等。FERGUSON等[1]指出,各类物品在销售环节中由于变质或损耗而造成的价值损失达到15%以上。据人民网报道,我国蔬菜和水果采摘后平均损耗率高达25%~30%,每年直接经济损失超过1 000亿元。对于分销商而言,物品在销售期间发生变质或损耗不仅导致采购成本上升,而且增加变质处理等日常运营成本,以及承担声誉形象遭受信任危机的机会成本损失。因此,易变质品的库存管理对企业经营具有十分重要的意义,引起了学者们的高度关注。
GHARE等[2]首次研究了易变质品的库存问题,指出具有常系数变质率的易变质品在库存期间因变质而发生的损耗与时间的负指数相关;COVERT等[3]和PHILIP[4]分别建立了变质率服从两参数和三参数威布尔分布的易变质品库存模型,从而将常系数变质率拓展到时变变质率情形;GOYAL等[5]和BAKKER等[6]对近年来易变质品库存管理的研究成果进行了系统的回顾与评述。早期的文献多数默认易变质品从进入存储系统便开始变质,而WU等[7]认为部分易变质品进入库存系统后会先维持原有特性和功能一段时间后才发生变质,并称之为“时滞变质品”。实际生活中的许多物品都是时滞变质品的例子,如蔬果、鲜花、牛奶等。随后,OUYANG等[8]考虑了确定性需求、不允许缺货且允许延迟支付的时滞变质品订货问题;MAIHAMI等[9]在需求依赖价格和时间、允许缺货与延迟支付的前提下,构建了时滞变质品定价和库存联合控制模型;CHUNG等[10]和MAIHAMI等[11]分别考虑了两级贸易信用下的时滞变质品库存决策问题;RABBANI等[12]和TASHAKKOR等[13]则各自建立时滞变质品的动态定价和库存控制模型;文献[14-16]研究了保鲜技术投资对时滞变质品订货与定价的影响;艾学轶等[17]构建了需求依赖变质时间的多种时滞变质品联合补货库存模型;许甜甜等[18]则尝试将数量折扣契约应用于时滞变质品供应链的协调。
关于第三方物流介入的三级时滞变质品供应链研究,陈晓旭等[19]讨论了物流服务商参与的时变需求变质品三级供应链模型,研究发现集中式决策并不能使该供应链达到协调;冯颖等[20]针对供应商、物流服务商和分销商组成的生鲜农产品三级供应链,建立了确定性需求、供应商主导的三方竞合博弈模型;马雪丽等[21]以供应具有季节性的农产品为研究对象,研究由“农户—第三方物流供应商—分销商”组成的三级供应链的协调问题。
本文以三级时滞变质品供应链作为研究对象,但与上述文献存在以下几点区别:首先结合时滞变质品的需求特征,构建需求率依赖于销售价格与变质时间的分段需求函数;其次考虑制造商与分销商按比例共同分担运输费用;最后针对供应链部分成员企业相互结盟的情形,探讨了制造商和分销商局部合作的供应链定价策略。
1 基本假设与符号说明
1.1 基本假设
本文构建的三级时滞易变质品供应链定价与协调模型基于以下基本假设:
(1)供应链各成员企业满足“理性人”和“完全信息”条件。
(2)运输服务商负责产品的运输,产生的运输费用由制造商和分销商共同承担。
(3)分销商的订货周期为单位时间,补货瞬时完成且不允许缺货。
(4)产品在销售期间发生变质,变质部分不占库存、无残值,但须承担处理成本。
(5)市场需求在产品变质前是销售价格的函数,在产品变质后受销售价格和变质时间共同影响。
(6)不考虑分销商的订单建立成本与制造商的生产准备成本。
1.2 符号说明
本文构建的三级时滞易变质品供应链定价与协调模型主要符号设定如下:
(1)分销商
D为时滞变质品的市场需求,是销售价格与变质时间的函数;
td为时滞变质品开始变质的时间点,0≤td≤1;
θ为时滞变质品的恒定变质率,0≤θ≤1;
p1为时滞变质品的单位产品销售价格;
h为时滞变质品销售期间的单位产品库存成本;
g为时滞变质品的单位产品变质处理成本;
q为分销商的订货批量;
I1(t)为时滞期内任意时刻t的库存水平;
I2(t)为变质期内任意时刻t的库存水平;
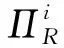
(2)运输服务商
p2为运输服务商收取的单位产品运输价格;
c2为运输服务商付出的单位产品运输成本;

(3)制造商
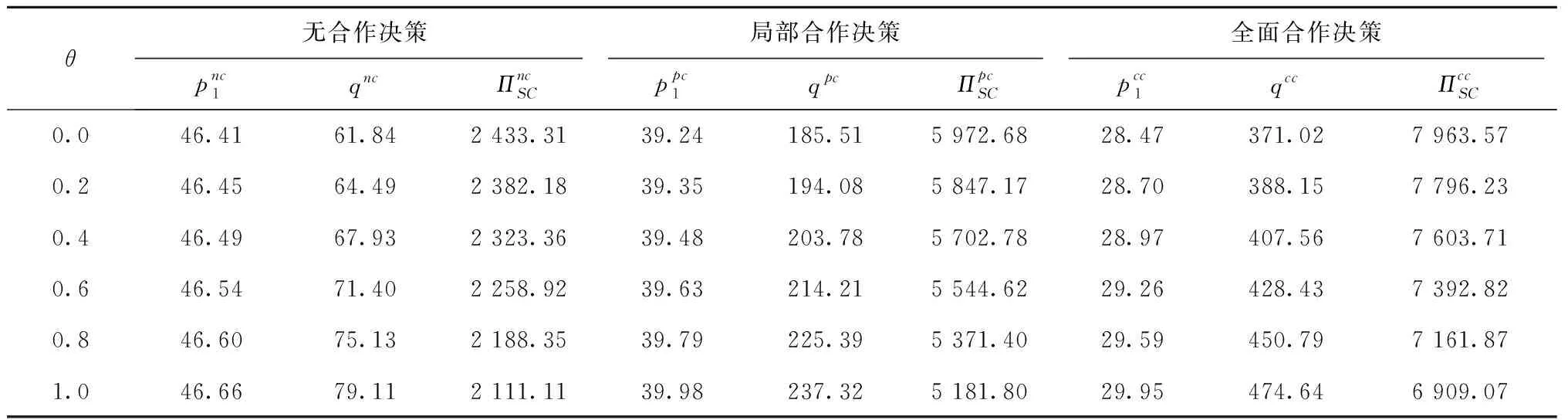
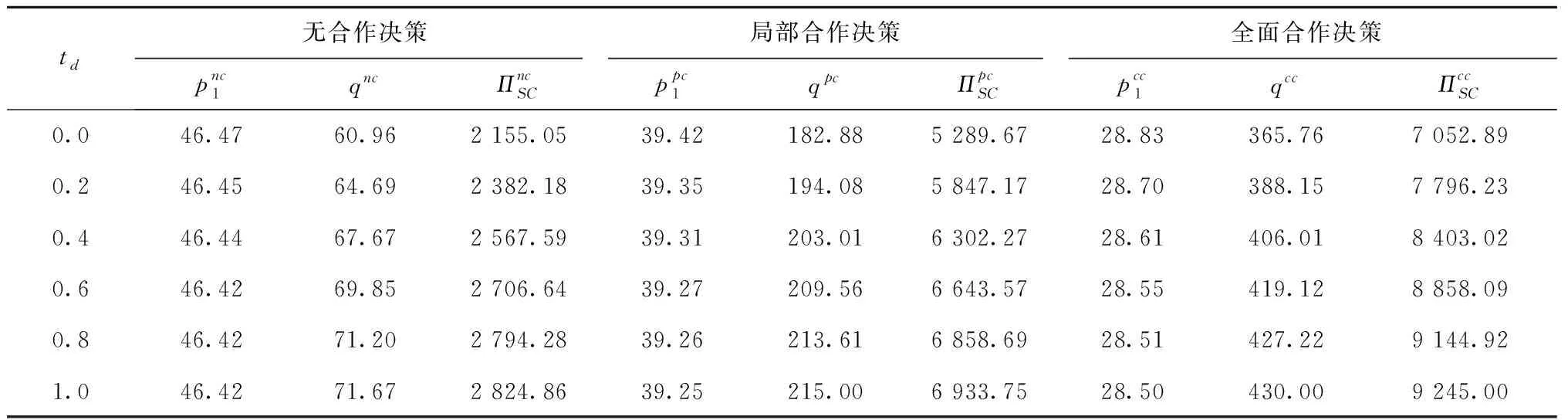
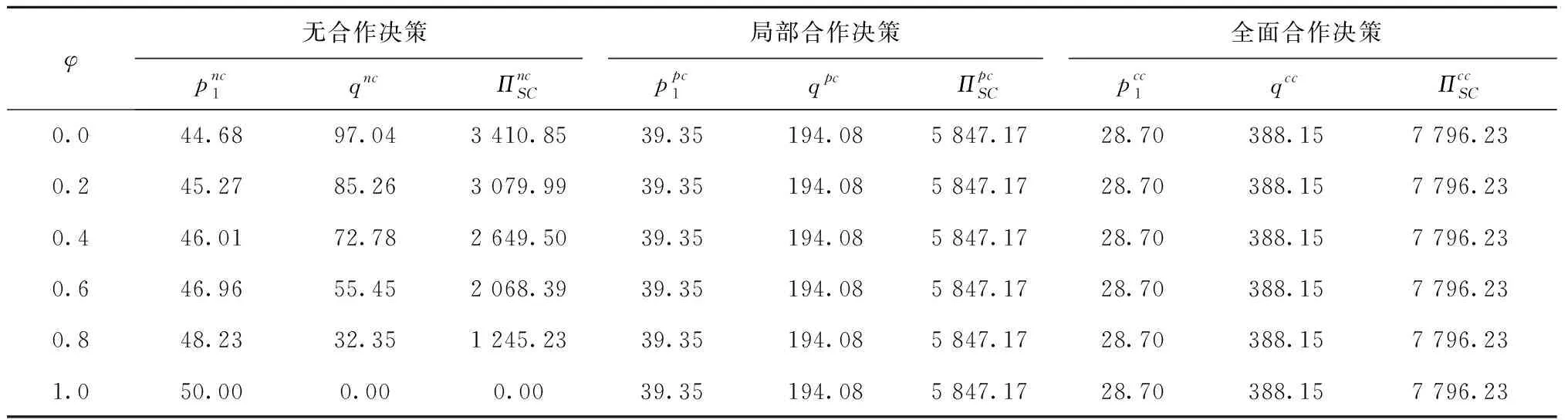
ω为制造商收取的单位产品批发价格,ω c1为制造商付出的单位产品生产成本,c1<ω; φ为制造商承担的运输费用比例,0≤φ≤1; (4)供应链系统 其中p1、ω、p2、q为决策变量。 本文讨论的三级时滞变质品供应链由一个制造商、一个运输服务商和一个分销商组成。其中,制造商以批发价格ω向分销商供应时滞变质品,分销商则在市场上以价格p1出售时滞变质品。分销商的订货周期为单位时间,每次订货批量为q,面临的消费者需求为D,市场处于出清状态。运输服务商负责产品的运输作业,对每单位产品收取价格p2的运输费用,制造商承担的运输费用比例为φ,分销商承担的运输费用比例为1-φ。模型的概念框架如图1所示。 以时滞变质品发生变质的时间点td为临界点,可将每个订货周期分为时滞期和变质期两个阶段。在时滞期t∈[0,td]阶段,时滞变质品的库存水平因市场需求而不断减少。在变质期t∈[td,1]阶段,时滞变质品的库存水平在市场需求及自身变质的双重影响下逐渐减少至零。假设消费者能够观察到时滞变质品发生变质,从而降低了对该产品的需求;且变质时间越长,产品变质现象越明显,消费者的需求下降越多。结合上述描述的时滞易变质品需求特征,建立相应的需求函数如下: (1) 其中:a为市场总潜在需求,b为需求对价格的敏感度,λ为需求对变质时间的敏感度,a、b、λ>0。 时滞变质品在每个订货周期内任意时刻的库存水平可表示为: (2) 求解上述微分方程得到: (3) 结合I2(td)=I1(td)可知,分销商每次订货批量为: (4) 分销商在一个订货周期内的成本由采购成本TC1、库存成本TC2、变质处理成本TC3及承担的运输服务成本TC4四部分组成,分别为: ω(a-bp1)td=ω(a-bp1)A, =h(a-bp1)B, =g(a-bp1)C, (e(θ-λ)-(θ-λ)td-1)+(1-φ)p2(a-bp1)td =(1-φ)p2(a-bp1)A。 分销商在一个订货周期里的销售收入为: 分销商在每个订货周期内的期望收益等于销售收入减去采购成本、库存成本、变质处理成本及承担的运输服务成本: ΠR=TR-TC1-TC2-TC3-TC4 =p1(a-bp1)M-ω(a-bp1)A-(1-φ) p2(a-bp1)A-h(a-bp1)B-g(a-bp1)C =(a-bp1)(p1M-ωA-(1-φ) p2A-hB-gC)。 (5) 运输服务商的预期收益等于运输服务收入减去运输成本: ΠL=(p2-c2)q=(p2-c2)(a-bp1)A。 (6) 制造商的预期收益等于产品收益减去生产成本及承担的运输服务成本: ΠM=(ω-c1-φp2)q=(ω-c1-φp2) (a-bp1)A。 (7) 本节将分别讨论供应链各成员企业在无合作、局部合作及全面合作3种决策模式下时滞变质品供应链的产品定价、供应链成员的期望收益与供应链系统的整体期望收益情况。 2.3.1 无合作决策 在无合作决策(No Cooperative Decision-making,NCD)模式中,供应链各成员企业间相互独立决策。制造商作为领导者,运输服务商和分销商作为追随者,供应链各成员企业之间形成3阶段Stackberg博弈模型。无合作决策的博弈过程为:首先制造商选择单位产品批发价格ω以最大化自己的期望收益,接着运输服务商公布单位产品运输成本p2以实现期望收益最大化,最后分销商确定销售价格p1和订货批量q使自身期望收益达到最大。 p1(ω,p2)= (8) p2(ω)= (9) ωnc= (10) 将式(10)代入式(9),解得: (11) 再将式(11)与式(10)代入式(8),解得: (1-φ)(c1+c2)bA)/4(2-φ)bM。 (12) 将式(10)~式(12)代入式(4)~式(7),分别解得: (c1+c2)bA), (13) (c1+c2)bA)2, (14) (c1+c2)bA)2, (15) (c1+c2)bA)2。 (16) 此时,供应链系统的期望收益为: ((aM-bhB-bgC)-(c1+c2)bA)2。 (17) 命题1得证。 2.3.2 局部合作决策 在局部合作决策(Partial Cooperative Decision-making, PCD)模式中,制造商和分销商相互合作,形成联盟进行联合决策,而运输服务商则独立决策。现实生活中不乏这种局部合作决策的案例,如制造商和分销商隶属于同一家集团公司,汽车主机厂和4S店就属于这种情形。局部合作决策的博弈过程为:首先运输服务商决策单位产品运输价格p2,然后制造商和分销商作为整体来联合决策销售价格p1和订货批量q。 证明“制造商—分销商”联盟的期望收益函数表示为: ΠR+ΠM=(a-bp1)(p1M-p2A- c1A-hB-gC)。 (18) (19) 将式(19)代入式(6),得到: bgC-p2bA)。 (20) 同理,可解得: (21) 将式(21)代入式(19),得到: (22) 再将式(22)与式(21)代入式(4)、式(18)、式(20),依次得到: (23) (c1+c2)bA)2, (24) (25) 此时,供应链系统的期望收益为: (26) 命题2得证。 2.3.3 全面合作决策 在全面合作决策(Comprehensive Cooperative Decision-making, CCD)模式中,时滞变质品供应链中各成员企业共同缔结联盟,追逐供应链系统的整体期望收益最大化,成员企业内部不存在转移支付。 证明在全面合作决策模式下,时滞变质品供应链系统的期望收益函数表示为: ΠSC=ΠR+ΠL+ΠM=(a-bp1)· (p1M-hB-gC-(c1+c2)A)。 (27) (28) 将式(28)代入式(4)与式(27),分别得到供应链系统的订货批量与期望收益为: (29) ((aM-bhB-bgC)-(c1+c2)bA)2。 (30) 对上述3种不同决策模式下的产品定价、订货批量及供应链期望收益进行比较,得到如下结论: 结论3表明,当变质率θ逐渐增大时,每个订货周期内产品因变质而损耗的数量增加,分销商会采取增加订货批量的方式来弥补损耗的数量以满足需求。另外,分销商通过提高产品销售价格来补偿部分损耗产品的成本,但由于市场需求受销售价格影响,提高销售价格的同时导致市场需求减小。即使订货批量增加且销售价格也上涨,因变质损耗影响和实际需求的萎缩导致供应链系统的期望收益仍然在逐渐减少。 结论4对于3种决策模式,满足: (2)qcc>qpc>qnc; 证明对无合作、局部合作、全面合作等决策模式下的产品定价、订货批量及供应链期望收益分别作差比较。 结论4得证。 结论4表明,随着时滞变质品供应链各成员企业之间合作程度的加深,单位产品销售价格逐渐降低,产品市场需求越来越大,供应链系统的期望收益也越来越高。因此,无论从经济效率(以供应链系统期望收益衡量)出发,还是从社会效益(以产品销售价格、市场供给数量衡量)视角考虑,完全合作决策要比局部合作决策与无合作决策更优。特别指出的是,局部合作联盟的形成并不能实现全局利益的最大化,供应链各成员企业的全面合作仍然是最优的决策模式。 由结论4可知,在3种决策模式中,全面合作决策所获得的供应链系统期望收益最大,局部合作决策其次,无合作决策最小。要保证供应链中各节点企业都自愿参与合作形成联盟,必要条件是合作后各节点企业分配的期望收益不小于非合作前各自独立决策的期望收益,且制造商和分销商的期望收益和要不小于“制造商—分销商”联盟的期望收益,即满足下列条件: 下面给出一种简单的协调契约来分配全面合作时的供应链系统期望收益。 ((aM-bhB-bgC)-(c1+c2)bA)2, (31) ((aM-bhB-bgC)-(c1+c2)bA)2, (32) ((aM-bhB-bgC)-(c1+c2)bA)2。 (33) 在由“制造商—运输服务商—分销商”组成的三级时滞变质品供应链中,参数设置如下:a=1 000,b=20,λ=0.5,td=0.2,h=2,g=1,c1=4,c2=2,θ=0.2,φ=0.5。其中各参数单位均为标准单位。将上述各项参数分别代入相应表达式,解得不同决策模式下的产品销售价格、订货批量及期望收益状况如表1所示。 表1 不同决策模式下的产品销售价格、订货批量及期望收益 由表1数据可知,随着制造商、运输服务商与分销商三者之间合作程度的逐渐深入,时滞变质品的市场销售价格在逐渐下降,市场需求的产品数量与时滞变质品供应链系统的期望收益快速增长。其中,局部合作决策时的市场需求量达到无合作决策时的3倍,而全面合作决策时的市场需求量又增长到局部合作决策时的2倍。在期望收益方面,得益于系统总体期望收益的增长,制造商、运输服务商与分销商的期望收益也随着各成员企业合作程度的深入而增加,但运输服务商在局部合作决策时的期望收益要比全面合作决策时更高。产生这种现象的原因在于,运输服务商在局部合作决策中担任领导者,对单位产品运输价格定价较高。 下面分别考察时滞变质品的特性参数变质率θ、时滞期td以及制造商承担的运输费用比例φ发生变动时对产品销售价格、订货批量及供应链系统期望收益的影响。 表2给出了变质率θ在0.0~1.0区间变化时对不同决策模式下产品销售价格、订货批量及供应链系统期望收益的敏感性分析。从表2可以看出,产品的销售价格对变质率的增加表现的不够敏感,订货批量随着变质率的增加有较大幅度增长,供应链系统期望收益会逐渐下降。比较3种决策模式可知,当供应链各成员企业合作程度加深时,产品的销售价格迅速下降,订货批量成倍增长,供应链系统的期望收益快速增加。 表2 变质率的敏感性分析 表2的分析结果表明: (1)变质率的变化对产品销售价格影响较小,但订货量受之影响增加较快,供应链期望收益随变质率增加不断下降,因此订货量增加不是市场需求增加引起而是因变质率增加被损耗掉,则供应链成员企业应比较降低产品变质率的成本投入与带来的收益增加,考虑投资诸如保鲜技术的可能性。 (2)对于给定的产品变质率水平,供应链各成员企业之间合作越紧密,通过供应链契约协调后能够获得的期望收益也越多,全面合作是各成员企业的最优选择。 表3给出了时滞期td在0.0~1.0区间变化时不同决策模式下产品销售价格、订货批量及供应链系统期望收益的敏感性分析。从表3可以看出,随着时滞期的延长,产品的销售价格呈下降趋势但降速较慢,订货批量和供应链系统的期望收益随时滞期的延长而明显增加。在相同的时滞期水平下,产品的销售价格随着供应链各成员企业间合作程度的加深而大幅度下降,订货批量和供应链系统的期望收益则因供应链各成员企业间不断加强合作而呈急速增加态势。 表3 时滞期的敏感性分析 表3的分析结果表明: (1)时滞期延长,虽然对促进分销商降低产品销售价格的作用甚微,但对刺激分销商增加订货量作用明显,并且供应链系统的期望收益也有大幅增加。 (2)考虑到时滞期的外生性,为了获得时滞期延长所带来的好处,制造商和运输服务商可让出部分收益来帮助分销商投资相关设备和技术,延长时滞期。 (3)供应链各成员企业间加强合作,不仅有利于提高消费者福利,如产品销售价格降低、市场产品供给量增加,而且也能保证成员企业自己获得更大的收益。 表4给出了制造商承担的运输费用比例φ在0.0~1.0区间变化时对不同决策模式下产品销售价格、订货批量及供应链系统期望收益的敏感性分析。从表4可以看出,随着制造商承担的运输费用比例持续增加,无合作决策模式下的产品销售价格不断上升,同时引起订货批量和供应链系统期望收益的急剧下降;而对于局部合作和全面合作两种决策模式而言,制造商承担运费比例的多少对其均不产生影响。就制造商承担的同一个运输费用比例来比较3种决策模式,可以看出,随着供应链各成员企业间合作程度的加大,产品销售价格出现较大幅度下降,订货批量和供应链系统的期望收益快速上升。 表4 制造商承担运输费用比例的敏感性分析 表4的分析结果表明: (1)若供应链各成员企业之间无合作意愿,应尽量减小制造商承担的运输费用比例,如此不仅可以降低产品销售价格,增加市场供给量,而且每位成员企业能够获得更多的期望收益。 (2)供应链各成员企业之间合作程度越深,经济效益和社会效益越明显,各成员企业和消费者受益越大。 日常生活中许多物品都属于时滞变质品的范畴,研究时滞变质品的定价策略与库存管理具有重要的现实意义。本文以“制造商—运输服务商—分销商”组成的三级时滞变质品供应链为研究对象,并构建符合时滞变质品需求特性的分段需求函数,分别考察了供应链各成员企业在无合作、局部合作与全面合作3种不同决策模式下的供应链定价与期望收益。研究结果表明,随着合作程度的不断加深,无论是供应链系统的整体期望收益还是时滞变质品的市场效率都得到提升。因此,供应链各成员企业之间合作程度越深,供应链系统的效率越高。本文提出一种全面合作的供应链系统期望收益分配方式,并对其有效性进行了论证。 本文给定时滞变质品在进入变质期后的变质率一直保持不变,便于模型的构建及后续计算,但这只是一个理想化的假设。部分学者已在其研究成果中开始讨论时变变质率的情形。另外,本文没有考虑允许缺货对供应链定价与期望收益的影响。允许缺货可以降低分销商的库存成本,但也会导致新的机会成本发生,因此允许缺货的结果往往比较复杂,后续研究将会考虑加入这些因素。
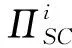
2 模型
2.1 模型描述
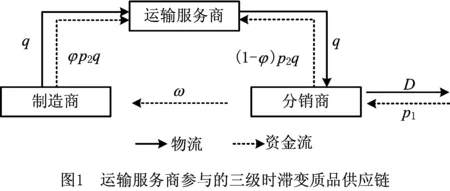
2.2 期望收益函数


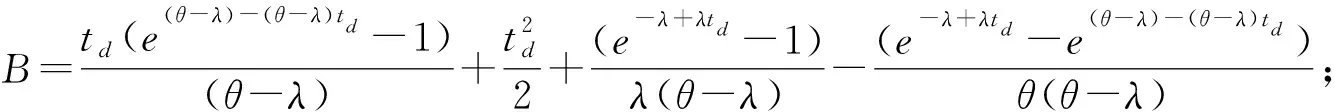


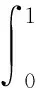

2.3 模型求解
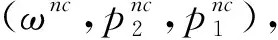
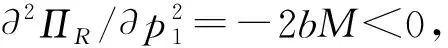
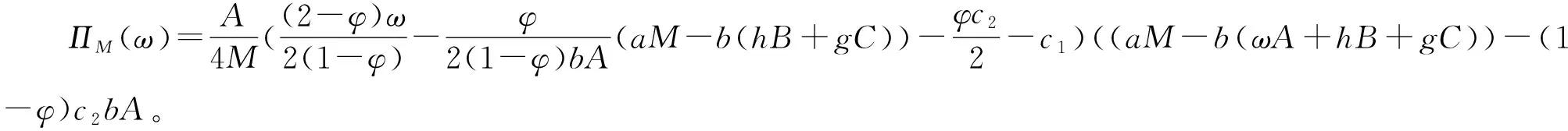
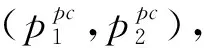
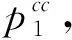
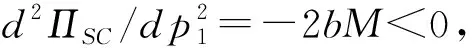
3 比较分析
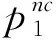

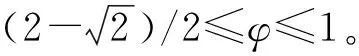
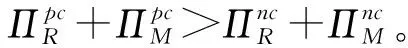
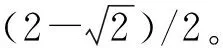
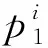
4 供应链协调契约

5 算例分析
5.1 参数设置与模型求解

5.2 敏感性分析
6 结束语
