基于粒子群优化算法的深海运载器模块化设计

2022-02-19张成郑鹏谷海涛高东勇

机械工程师 2022年2期

张成，郑鹏，谷海涛，高东勇

（1.沈阳工业大学机械工程学院，沈阳 110000；2.中国科学院沈阳自动化研究所，沈阳 110000）

0 引言

深海运载器是一款承载多任务载荷的深海运载平台，具备承载大、下潜深、执行任务多样、潜航时间长等特点。深海运载器根据其任务以及工况的不同，需要携带不同的工作载荷。而不同的工作载荷存在质量、尺寸、转动惯量等差异，运载器整体内部空间有限，在满足运载器整体运动特性稳定的前提下，如何合理地将工作载荷放置在运载器内部，使内部空间利用率达到最大，是本文的主要研究内容。

目前国内外关于运载器内部空间模块化布局的文献较少。本文基于工作任务的不同，拟计划将运载器载荷分为AUV模块、电子仓模块、雷达仓模块、滑翔机模块、电池模块、动力模块等诸多模块。对于单一模块内部分布着工作载荷、挂点、充电和通信部件，属于较多的多物件分布问题，针对目标函数计算量大、计算难度高等问题，本文采用粒子群算法进行求解，以提高运算精度和速度。

1 布局问题数学模型

1.1 负载配置的数学模型

载荷在配置过程中，考虑载荷的发射以及回收等工作空间，同时为了减少载荷外形尺寸的差异对计算精度及计算量的影响，现将AUV等载荷简化为同等长、宽、高的圆柱体，将过载部件等简化为长方体。声纳、电子仓因为其需要的特定密闭环境，将所处区域简化为球体，具体如图1所示。

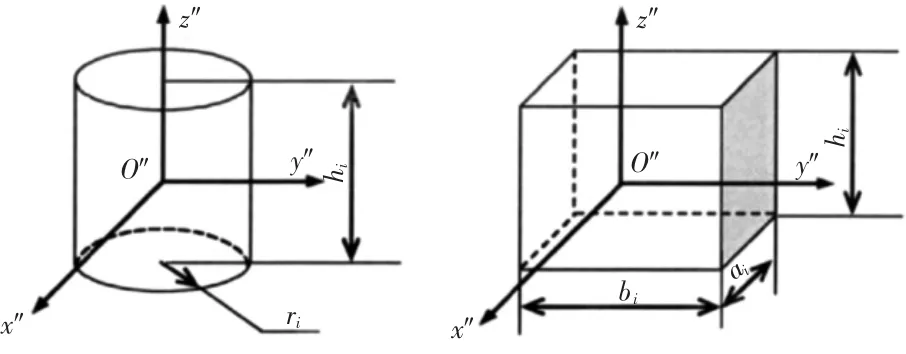
图1 工作载荷自身坐标系示意图

为了方便考虑与限制每一个载荷的位置，建立相应的坐标系[1]如下：

Oxyz为参考坐标系：O为坐标原点，选在深海运载平台的几何中心上；z轴为深海运载平台的纵向对称轴；x轴垂直于纵轴平面；y轴与x轴、z轴呈右手直角坐标系。

O′x′y′z′为深海运载平台的坐标系：O′为坐标原点，位于深海运载平台的质心处；z′为深海运载平台的纵向对称轴，与z轴平行或重合；x′轴、y′轴分别与x轴、y轴平行。

O″x″y″z″为计算单元胞自身坐标系：O″为坐标原点，位于各计算单位的质心处；z″为计算单位的纵轴，z″轴与z轴平行；x″与x轴夹角为Φ；y″与y轴夹角为Φ。

设xi、yi、zi分别为载荷i的质心在参考坐标系中的坐标。假设工作载荷都为刚体同时质量分布均匀，mi为工作载荷的质量。αi∈［0，π］为各工作载荷自身坐标的x″轴与参考坐标系的x轴的夹角，设定逆时针方向为正。（xc，yc，zc）为运载器全部部件质心坐标在参考坐标系中的理论期望值。θx′（X）、θy′（X）、θz′（X）分别为运载器惯性主轴与运载器坐标系的夹角。ΔJ为运载器对运载器坐标系的转动惯量的容许值，Jx′（X）、Jy′（X）、Jz′（X）分别为运载器对运载器坐标轴的转动惯量。

圆柱体载荷i的转动惯量计算公式如下[2]：

1.2 多目标优化模型

该布局方案的主要目标是满足惯量特征的容许值条件。

1）转动惯量（全舱对运载器坐标系的转动惯量）。

式中：J为所求目标函数；Jx′、Jy′和Jz′分别为全舱对运载器坐标系x′轴、y′轴和z′轴的转动惯量。

并需要满足以下约束条件。

2 粒子群算法求解

2.1 粒子群优化算法介绍

粒子群优化算法的求解思路为模拟鸟群的捕食行为，鸟群通过自身的经验以及种群之间的交流来不断地修正自己与目标食物之间的距离，从而尽快地到达食物所在的地点。而鸟群从初始位置到食物之间的路径称之为搜寻路径。在本文中，鸟群的初始位置就是设定的粒子初始数值，在计算的过程中，鸟的路径（粒子的迭代过程）作为自变量组合，而食物所在地点称之为函数最优解，那么每只鸟在寻找的过程中通过不断地修正自己的方向和速度，从而达到距离食物更近的地点，这个地点称为跟踪极值，算法通过不断地比较极值距离与最优解集之间的距离值从而修正粒子的方向，从而找到最优解。

1）参数设计。

种群数量：粒子群算法中的粒子的数量决定着寻优的速度，但粒子过多会导致计算量过大，因此初始种群取100。

迭代次数：迭代次数是粒子群算法中的修正过程，本文中迭代次数取500。

学习因子：学习因子是指原有粒子在原来基础上进行新的迭代过程中的一种占比，一般取1。

位置限制：位置约束为粒子寻优的空间，即自变量的取值范围，本文中规定横、纵坐标中的顶点。

2）速度与位置更新。

速度和位置更新是粒子群算法的核心，其原理表达式和更新方式如下[11]:

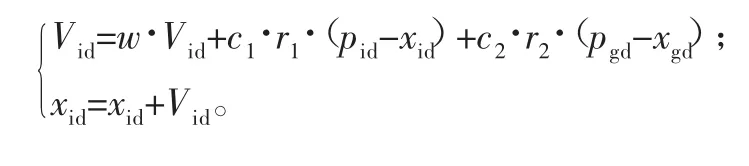
式中：Vid为本次粒子的速度值；w为惯性权重；Pid为粒子的当前所在位置；xid为粒子的前一次位置；c1、c2为学习因子；r1、r2为修正因子。

每次迭代结束，粒子都会出现新的速度及位置坐标，得到的坐标及速度值会作为下一次迭代的初始值。在迭代的过程中出现速度或者位置超出约束边界的情况，粒子会被自动拉回靠近边界的点。

2.2 载荷配置方法

对于单模块内部的载荷配置，采用粒子群算法进行优化设计。粒子群算法主要有3个主要的特点：1）不要求目标函数的连续性，可微性；2）算法具有内在的并行性；3）基于正反馈原理进化机制，有利于搜索最优解。

在本文中，运载器中的载荷在布局完成之后，要求装填方案的惯性夹角及质心偏移量在允许范围之内，同时保持运载器的整体转动惯量最小。即使质心偏移量f3（x）、f4（x）和惯量夹角θ′x、θ′y、θ′z都尽可能小。

2.3 MATLAB优化求解

设深海运载器尺寸为长12 m、宽2.4 m、高2.4 m的矩形空间。要在矩形空间内放置30个待布物，其中相同AUV，滑翔机等采用统一尺寸，具体尺寸如表1所示。运载器内部待布物均为自由布置。另外整舱质心偏差量为Δxc=Δyc=Δzc=3 mm，动平衡度许用值Δθx′=Δθy′=Δθz′=0.03 rad/s。运载整体质心坐标为（0，0，0）[13]。

表1 深海运载器载荷质量和几何参数

针对上述问题，采用MATLAB软件进行编程，物品初始位置由计算机自动生成，达到最优结果之前运行一次应记录一次优化结果。具体算法参数设置为：种群粒子数为15（分为3组，每组5个粒子）；迭代数为500次，最终结果采用独立运行20次后的平均值；参数设定为c1=c2=2，ω=0.8计算仿真结果如表2所示。

表2 运载器载荷布置方案

深海运载器整体转动惯量作为运载器布局的目标函数，转动惯量的值随迭代过程图像如图2所示。

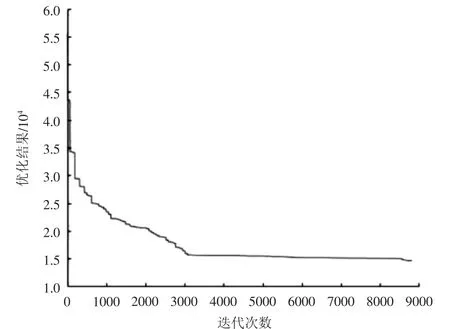
图2 转动惯量变化图

根据图2可以看出转动惯量迭代3000次处于最小状态，其运载器内部载荷位置坐标生成位置图如图3所示。

图3 AUV模块内部分布图

可以看出运载器内部呈现放射状对称分布方式。考虑运载器内部模块划分规则，将同一尺寸物品进行小型化约束，可以得到单独的AUV模块的布局方案如图4所示。

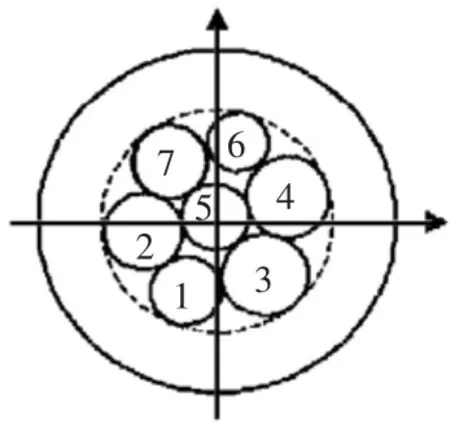
图4 AUV设计理论图

3 AUV模块设计

AUV是深海运载器中最重要的工作模块，其中大部分的探测任务均来自于AUV。AUV工作时需要从深海运载器内部脱离，进行单独的运动。所以考虑到AUV发射和回收过程并结合优化结果，设计环形放射性AUV布局方式，如图4所示。主体承载架由液压缸和支撑杆件组成，待机状态以环形分布在AUV模块中，如图5、图6所示。等到工作时由液压缸托起至发射位置，进行发射，方式如图7所示。承载架两侧采用伺服电动机进行驱动，可进行角度转动，以实现发射AUV的连续性。