大水深自升式钻井平台隔水导管稳定性及安全性分析

宋光立，刘军波，王毅

（中海油田服务股份有限公司，天津 300452）

0 引言

近年来，随着海洋近海勘探区域逐步向深水迈进，国内自升式钻井平台作业水深也逐渐超过100 m水深限制，400 ft自升式钻井平台逐年增加。这些高端自升式钻井平台在设计之初就考虑了极限风暴条件下的生存，而与之配套使用的隔水导管的安全性缺鲜有分析。如拓展这些高端自升式钻井平台的作业范围，隔水导管成为限制其发挥作业能力的短板。因此，为了保证海上钻完井作业安全，提升现有高端钻井平台的作业能力，需要对设计作业水深超过100 m的自升式平台使用的隔水导管进行受力分析与强度校核，计算其在不同水深范围和海洋环境下的使用参数，以确保其满足海上钻完井作业要求，为海上工程施工提供指导和安全保障。

1 中国近海海流分布特征及极值海流调研

国内某JU-2000E型400 ft非自航自升式钻井平台，由主船体和3条桁架式桩腿构成，平台作业期间处于站立状态，在风暴条件下主要受风载和波浪动载的作用，其站立风暴的设计标准为：水深为121.92 m、波高为18.29 m、波浪周期为15.5 s、最大风速为51.44 m/s。

海上极值流速发生在台风期间，通常设定年极值流速由风暴潮与天文潮耦合形成。我国渤海属于内海，黄海为半封闭的陆架海区，黄海受大浪影响要比渤海明显。通常情况下黄海海区内海流主要是潮流，其多年一遇极值流速由潮流和大风情况下的风海流共同影响形成。根据相关模型，推算黄海水域百年一遇的极值海流接近2 m/s[1]。东海海流最大处在台湾海峡及附近水域的沿岸流，采用POM三维海流数值模式，推算浙江温州丽水海域百年一遇的表层极值流速接近2.9 m/s，底层极值流速不超过1.4 m/s；采用三维风暴潮流模型，推算浙江象山港海域50年一遇的表层极值流速为3.23 m/s，底层极值流速为2.22 m/s[2]。南海夏季表面流为东北流，冬季为西南流，其西部海流比东部强，相关文献推算南海珠江口海域内百年一遇表层极值流速约为3.6 m/s，底层极值流速约为1.6 m/s[3-5]。

因此，在隔水导管抗拉抗弯强度计算模型中，宜选取南海海域极值流速与隔水导管稳定性失效前所能承受的极限值对比，确定其安全系数及使用参数。

2 风暴条件下自升式钻井平台井口最大位移

目前世界各国广泛使用三桩式海洋平台——JU2000E自升式平台，通过建立平台三维有限元分析模型，对平台施加50年一遇风暴环境载荷，计算风暴自存条件下平台的水平偏移量。

刘运祥[6]、王恒等[7]采用有限元分析软件对400 ft自升式钻井平台进行结构静力分析，在风暴自存工况下(水深为91.44 m、波高为10.67 m、波浪周期为13.50 s、风速为50 m/s)，不考虑附加弯矩情况下计算平台最大偏移为0.3 m左右。

而陈营营等[8]认为钻井平台的桩腿还承受着因自身重力所引起的附加弯矩(P-Δ弯矩)作用，在风暴环境载荷下(水深为91.44 m、波高为10.67 m、波浪周期为13.5 s、风速为41.44 m/s)，考虑附加弯矩影响，计算出上述平台结构最大偏移为1.56 m。国内某400 ft自升式钻井平台在其风暴自存分析报告中，认为在风、波浪、海流和动力作用下，平台横向偏转会导致额外的倾覆力矩和下导轨下方支腿的额外弯曲力矩。考虑P-Δ力矩作用下，平台偏移计算结果如表1所示。

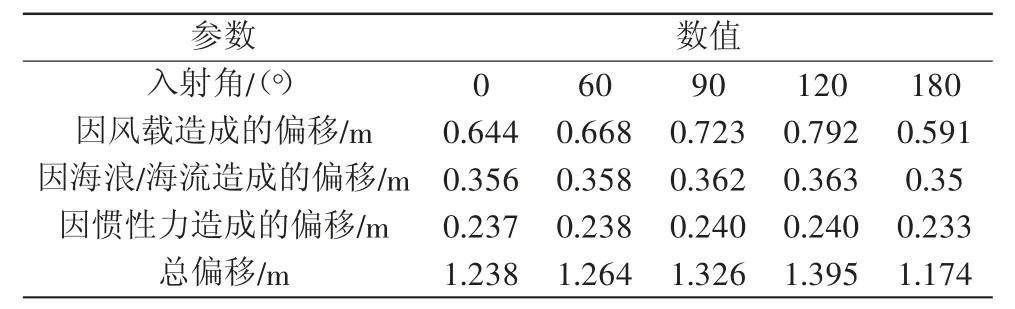
表1 考虑P-Δ弯矩作用的平台偏移量计算结果(水深107 m、浪高17.4 m)

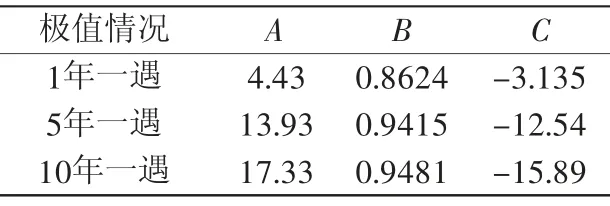
表2 多年一遇流速极值剖面参数

由此得到，400 ft钻井平台在120 m水深海域作业期间，在风暴站立工况下，井口小平台处的最大偏移接近1.4 m，对于上端固定在井口平台的隔水导管而言，这种偏移幅度不能忽略不计。在实际作业中，为降低因这种偏移带来的影响，往往使用张力器对隔水导管顶部施加上提力。

3 隔水导管受力分析

3.1 隔水导管力学受力模型的建立

由于隔水导管处于海洋环境中，固定端位于泥面处，顶部与防喷器连接。对于水深超过100 m的作业环境中，隔水导管顶部考虑施加轴向上提力。为简化分析，将隔水导管与海底连接视为固支约束，与防喷器连接处视为简支约束，轴向自由。其力学计算模型如图1所示。

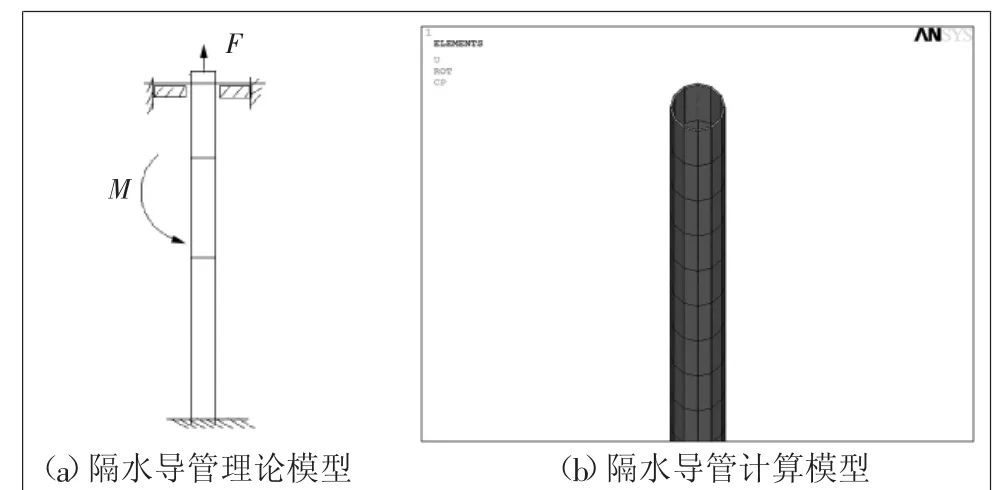
图1 隔水导管抗拉抗弯强度计算模型

利用ANSYS结构分析软件建立隔水导管力学分析模型，采用shell43壳体单元进行结构非线性分析，采用Mises屈服准则、经典双线性随动强化准则、理想弹塑性材料进行分析。

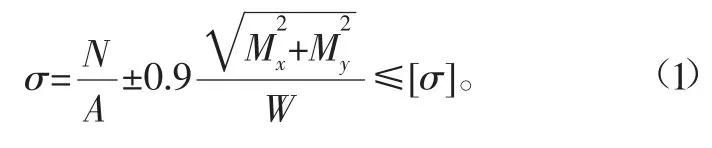
隔水导管可视为圆管型构件，当它轴向受拉或受压，且在2个平面内受弯，其轴向应力强度校核公式为式中：σ为轴向应力，MPa；N为计算截面的轴向力，N；Mx、My为计算截面分别绕X及Y轴的弯矩，N·mm；A为圆管的截面面积，mm2；W为圆管截面的剖面模数，mm3；[σ]为强度许用应力，取值为0.6σs，MPa。

圆管形构件在轴向力和弯矩联合作用时，稳定性校核的公式为

由于隔水导管直径变化不大，因此作业水深和本体屈服强度是影响其稳定性许用应力大小的关键参数。

考虑在极值海洋环境下，隔水导管本体主要承受海流作用，因此需要分析风暴极值工况下海流流速分布特征，并将其带入圆管稳定性校核公式，确定隔水导管的最佳使用参数。

3.2 海流流速的设定

在开阔静水海面上，如果没有实测数据，通常取Vw=0.01V风。该公式在一般气象环境载荷下具有参考意义，不适用于台风、飓风等恶劣天气。

刘明等[10]在分析南海流花海域海流特征时，利用ACER(Average Conditional Exceedance Rate)方法对分层流速的多年一遇极值进行了分析，发现海流流速空间分布形态总体上接近于剪切流，随着海水深度加深，海流极值流速总体呈递减趋势，分析发现海流形成的主导因素是潮流和风生流，推荐了拟合公式如下：

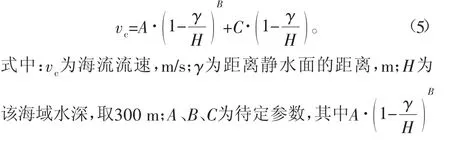
将水深数据代入上述公式中，可以得到表层流速、中层流速和底层流速之间的关系大致为1∶0.6∶0.2。由于该公式数据来源于监测系统获取的海流监测数据，其中风生流数值相对偏小，导致表层流速数值小于风暴条件下的实际极值海流数据。

以上观点均认为海流空间分布形态总体接近剪切流，为简化计算，本文假设海流速度沿水深线性倒三角分布，定义水面流速为V，中部流速为V/2，底部流速为0.2V。

此外，刘清友[11]分析波高、波长和波周期等波浪参数对深水隔水管的最大弯矩、最大应力和最大转角的影响，认为这些参数的影响有限，可以忽略不计，因此本文不考虑波浪参数对隔水导管力学特性的影响，而风载对隔水导管的影响主要是通过海水表面流的方式施加，即所谓的风生流，已考虑到海流流速中。

3.3 考虑海流作用下隔水导管整体强度计算

隔水导管处于海洋环境中，下端与防喷器连接。为简化分析，将隔水导管与防喷器连接处视为简支约束，上端水平方向位移受到约束，轴向自由，建立海流作用下的力学计算模型如图2所示。

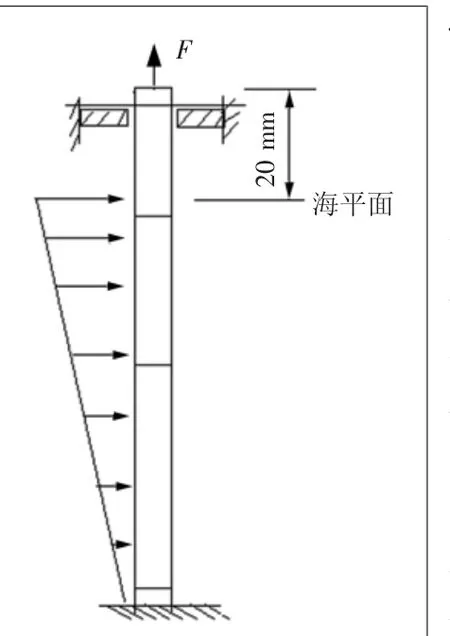
图2 考虑海流作用下的隔水导管整体力学模型

将海流表面流速V作为变量输入ANSYS循环计算流程(如图3)，设定结构最大应力小于隔水导管管体屈服强度，在隔水导管顶部施加轴向拉力，使管串受力中和点位于泥面以上5 m处。

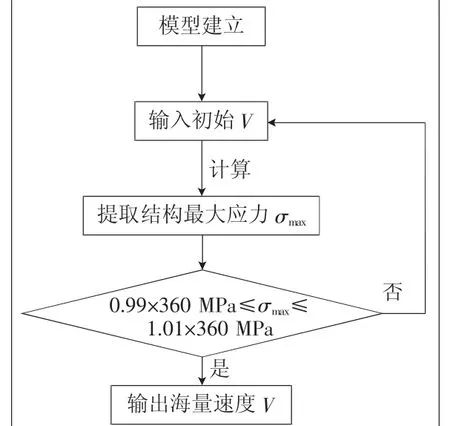
图3 采用ANSYS循环计算流程

计算结果显示，在设定条件下，隔水导管的最大负弯矩位置在泥线附近的固支处，最大正弯矩在水面以下13 m左右，这是隔水导管在作业期间承受交变应力最大的位置，也是隔水导管达到屈服强度时最危险位置。在海流作用下，其应力分布云图和弯矩分布云图如图4所示。

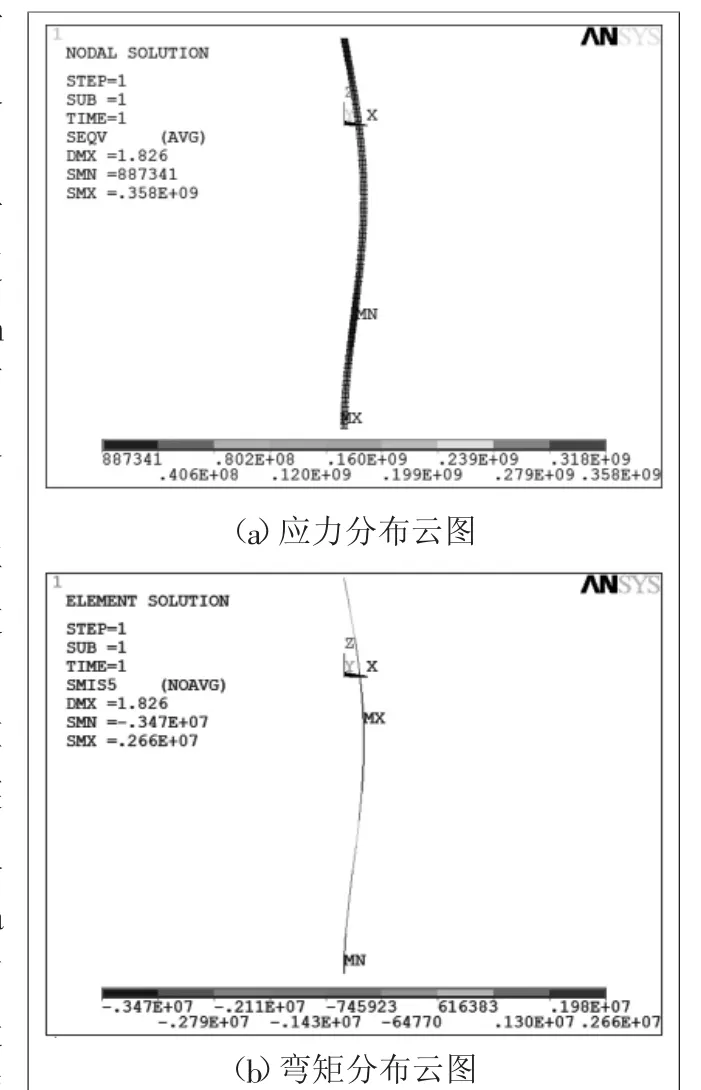
图4 隔水导管作业期间在海流作用下的应力分布云图和弯矩分布云图

计算中发现上述规格的B级钢隔水导管在120 m水深海域作业时，可承受的表层极限海流为3.24 m/s小于南海百年一遇表层极值流速3.6 m/s；在100 m水域作业时，可承受的表层极限海流为3.8 m/s因此不建议将其用在水深超过100 m海域作业。

在上述计算中输入不同水深条件，得到屈服强度为360 MPa隔水导管整体结构屈服时可承受的极限海流速度如表2所示，隔水导管结构屈服时的极限流速分布呈幂函数变化（如图5）。

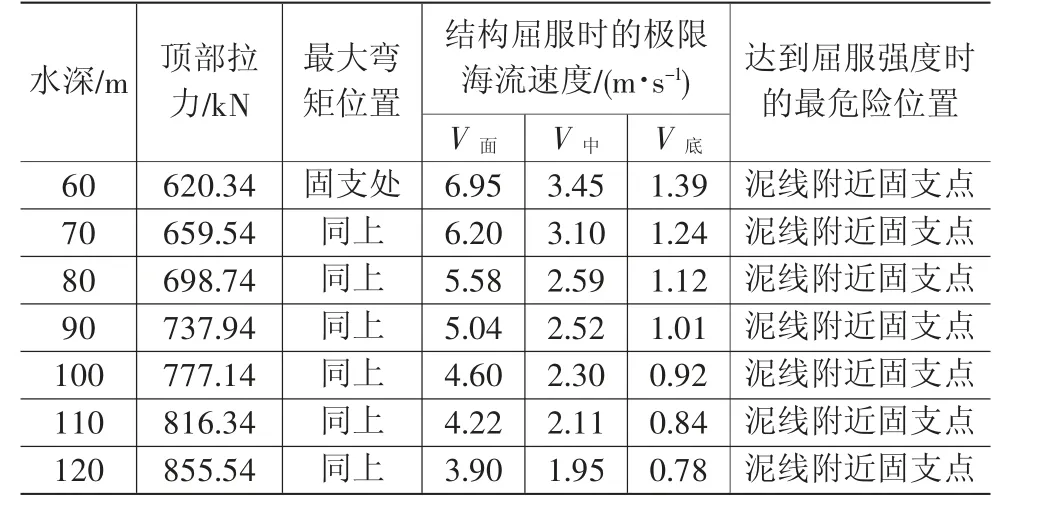
表2 隔水导管在360 MPa的屈服强度下能承受的极限海流流速表

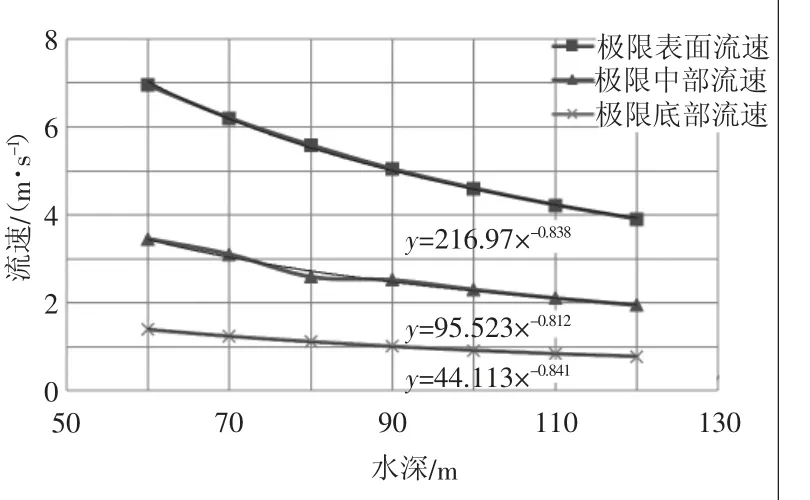
图5 不同水深范围下隔水导管屈服时的极限流速分布规律

4 结语

1）我国作业水深400 ft高端自升式钻井平台在极限风暴站立工况下，通过提高和保持隔水导管截面轴向拉力可增加管体抗弯能力，提高其风暴极限工况下的生存能力。

2）隔水导管的作业水深和本体屈服强度是影响其稳定性许用应力值的关键参数，在一定水深范围内，提高隔水导管本体屈服强度可以提高管体稳定性。

3）随着作业水深增加，隔水导管承受的极限海流速度呈幂函数降低，且极限表面流速下降幅度要明显大于极限底流下降幅度，显示表层流对隔水导管的弯矩影响更大，因此井口平台的张力器拉力值应随着水深增加而增加。

4）在极限风暴站立工况下，隔水导管本体受交变应力影响最大的两处地方位于泥线固支和水面以下13 m左右，作业结束后建议对这两处的隔水导管本体进行金属疲劳检测或降级使用。