非球面接触测量中触发式测头预行程误差补偿研究

张铁建，于正林，张茂云，唐晨

（长春理工大学机电工程学院，长春 130022）

0 引言

非球面光学零件凭借其在光学系统中可有效地矫正系统像差，扩大系统的视场角度，减轻系统整体质量和缩小系统体积等作用，被广泛应用于各高精尖科技领域[1]。非球面面形检测技术作为其加工工艺的一部分，如何准确、快速、高效地检测出非球面零件的面形信息，是许多专家学者一直重点研究的难题。

根据检测手段的不同，主要分为机械接触式测量和光学非接触式测量[2]。光学非接触式测量方法众多且测量精度可到达纳米级别，但光学测量很容易受到空气介质和灰尘的影响，对于被测零件的面形精度要求较高，且设备成本较高，一般应用在精密抛光阶段对最终成型的零件进行测量。而接触式测量具有更高的适用性，虽然存在测头接触变形误差和划伤零件表面的风险，但是该方法得到的数据可靠且抗干扰能力强，故在实际加工过程中接触式测量更加可靠，主要应用于零件的精磨阶段[3]。

本文在非球面零件成型铣磨阶段应用接触式触发测头对非球面面形进行测量，针对测量过程中触发式测头预行程误差进行分析，通过对测杆弯曲变形和测球变形的受力分析，建立预行程误差模型，通过对触发力的理论推导，精确计算出预行程误差值，研究预行程误差补偿方法。

1 触发式测头

根据测量需求，测头的基本使用要求有：具有良好柔顺性，即当测头接触零件表面时，测头受到较小的测量触发力就可以使测杆发生偏移产生信号，并允许测头在离开零件表面前有时间减速；良好的可重复性，即使探针在不接触零件时始终返回到初始状态。

图1所示为触发式测头三维模型图，该测头将触发方式与机械结构完全独立，消除由于长期使用带来的磨损误差，可以提高测头的可重复性。图2所示为测杆定位机构，该机构主要采用推力轴承只能限制一个轴向自由度，而对其它5个自由度无限制的原理。

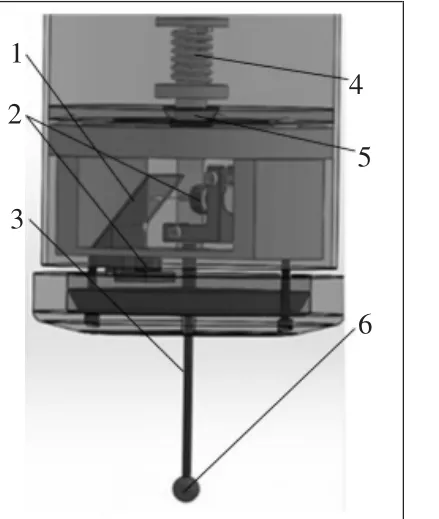
图1 触发式测头三维图

图2 测杆定位机构图

当测头处于“零”位状态时，轴承板受弹簧缓冲机构提供的弹簧预紧力和3个均匀分布的小球提供的支持力牢牢固定在测头中线的位置上，此时光源发射光线通过测杆的小孔经预先设定好的45°反射板，根据光线反射原理，入射角等于反射角，光线正好可以射至传感器接收端。当测头接触工件时，随着接触力的增加，直到触发力打破测头内部平衡测杆发生偏移，导致光线射到反射板的入射角度改变，从而反射光线无法经预设线路到达传感器，测头检测到下降沿信号，并将此时工作电路状态变化状态传出。当测头离开工件，触发力消失，由于测杆的偏转非常小和3个小球的定位效果，测杆又回归“零”位，等待下一次测量。

2 预行程误差建模

在实际测量过程中，由于测头自身机械响应的滞后，当接触到被测零件表面时并不会立即发出触发信号，故从测头接触到被测零件表面到被触发这一过程被称为测头的预行程误差。由于影响测头预行程误差的因素众多，如测杆弯曲位移误差和测球接触位移误差等，为了精确计算测头预行程误差，针对不同误差源进行数学建模对误差进行定量分析是十分必要的[4-5]。

2.1 触发过程中测头机构受力分析

对测头模型进行简化分析，触发式测头触发机构可近似看成弹簧提供的预紧力和3个均匀分布在机架上的小球将测杆固定，当接触工件时，测杆受力使测杆具有X、Y方向及Z轴正方向偏移的能力，因此可以完成XY平面任意方向及Z轴正方向的测量。如图3所示，A、B、C为3个接触球副对称分布在轴承座上，设测杆为Z轴且竖直向上为Z轴正方向，与测杆垂直的平面为XY平面且OA方向为X轴正方向，忽略探针自重的影响，测杆长度为L，弹簧预紧力Fs作用在轴承板中心点，方向与Z轴正方向相反，F（θ，γ）为测头与被测零件表面接触时的触发力，θ为测量触发力在XY平面内与X轴正方向的夹角，γ为测量触发力与Z轴正方向的夹角。

图3 触发式测头受力图

根据非球面零件的子午线检测原理可知，测头与非球面表面接触点实际上就是过非球面母线上各点的坐标。非曲面零件测量模型如图4所示，为非球面零件测量模型图，从图中可以看出，非球面零件表面被测点切线与X轴夹角α和测量触发力方向与Z轴夹角γ相等。根据非球面零件一般表达式可以计算出角α。故角γ可以表示为

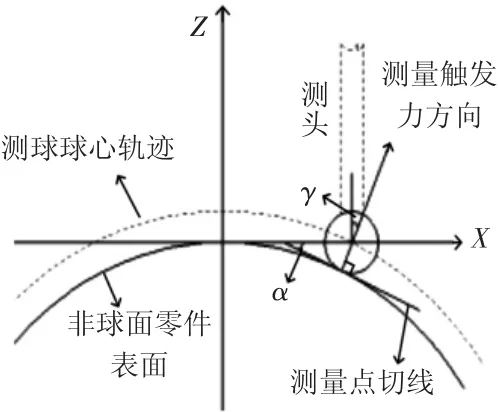
图4 测量模型分析图

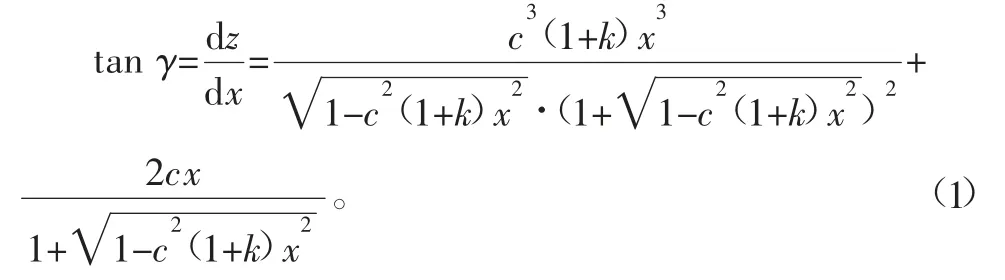
1）测杆弯曲位移误差。

实际测量中，在接触测量力的作用下测杆会发生微小的弯曲变形情况，从而在测量过程中会产生由测杆弯曲变形影响带来的误差，下面对测杆弯曲位移误差进行分析。

图5 测杆弯曲变形示意图

2）测头接触变形误差。

当测头接触到被测零件表面时，在测量接触力的作用下测头与被测零件表面产生接触变形，从而在测量过程中会产生测头接触变形误差。

与被测零件表面局部构建的接触受力变形示意图如图6所示。设测球半径为r1，非球面零件的等效半径为r2，由于r2>>r1，可以将被测件接触处看作平面，也就可以将图6中的球与球接触变成球与面接触的问题，即曲率1/r2=0，所以相对曲率半径r满足1/r=1/r1+1/r2，即r=r1。

图6 测球与被测件表面局部接触变形示意图

根据Hertz方程可有：

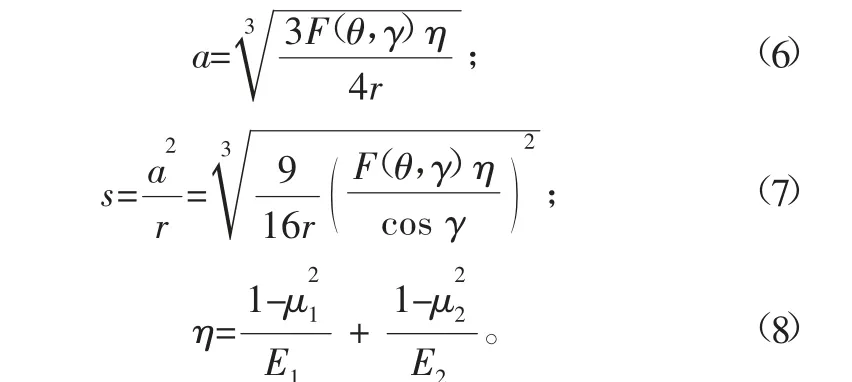
式中：a为接触面半径；s为局部接触变形量；r为测球半径；μ1、E1、μ2、E2分别为测球与被测件的泊松系数和弹性模量。

综上所述，对造成预行程误差的原因，测杆弯曲位移误差和测头接触变形误差进行了建模分析，可以得到预行程：

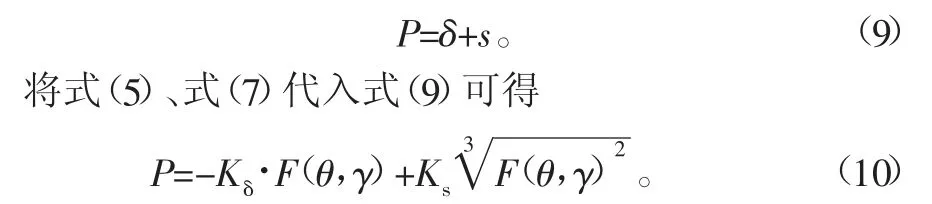
式（10）即为触发瞬间预行程函数模型，通过模型可以观察出触发式测头预行程误差的大小与测杆的长度L、测杆直径D、测球半径r、测量触发力F（θ，γ）及材料和非球面表面被测点切线角有关。除非球面表面被测点切线角和测量触发力的大小外，其他影响参数在测量过程中都定量，故对非球面零件测量过程中产生的预行程误差只需要研究这两个因素的影响即可。通过式（10）可以看出其对预行程影响最大的就是测量触发力，测量触发力与预行程成正比关系，即要想求出测头预行程误差必须知道测头的触发力。

2.2 测头触发力推导

对本课题所设计的光电式触发测头结构分析可以知道，在无任何外力的作用下，测头内部轴承板在弹簧预紧力和3个球支撑副的作用下，牢牢固定在测头内部，此时激光光线正常折射到光线接收端，处于待工作状态；当测头与被测零件表面接触时，会产生测量接触力，当此测量接触力逐渐增加直到破坏测头内部的平衡状态使测杆发生偏转，当测杆发生一定量的偏移时，接收端接收不到激光信号，从而使测头状态由高变低发出触发信号。根据上文对测头受力情况分析可知，测头的测量触发力对预行程误差影响非常大，所以必须对该力进行理论推导。

如图7所示，H为测球中心距支撑平面的距离；G为测杆自重，其方向竖直向下；Fs为测杆所受弹簧预压力，其方向竖直向下；fs为轴承板与弹簧缓冲机构的摩擦力；FA、FB和FC分别为小球对测杆的支反力，其方向始终与测杆方向一致；fA、fB和fC分别为与各支撑点的摩擦力，其方向与所产生的运动方向相反。

根据图7所示受力情况，当测头随着F（θ，γ）的增大，小球与轴承板产生相对运动趋势，当某一点支反力为0时，此时必定至少有一个触点脱离接触。当测量触发力没有达到破坏测头内部平衡时，测杆在空间上所受的合外力为0，合外力矩也为0。即Fx=0，Fy=0，Fz=0，Mx=0，My=0，Mz=0，可列出测头触发时关于未知量支反力FA、FB和FC的空间力学方程式：

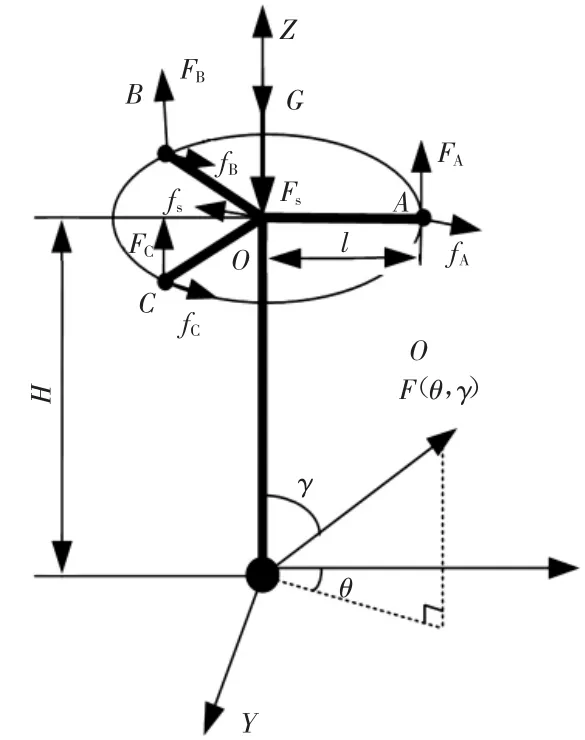
图7 测头触发受力分析示意图

根据测头触发时，3个接触球必有至少一个脱离接触，想解式（12）、式（13）和式（14），必须分析出在不同方位角情况下各支反力的情况。根据图7坐标系分析，在不同的接触方位角的情况下，对各支反力分析如表1所示。

表1 三维触点接触方位与开启情况

根据接触方位角θ与触点开启情况，当θ在300°～60°之间时，FA=0；当θ在60°～180°时，FB=0；当θ在180°～300°时，FC=0。

将上述对各支反力情况分析结果代入式（11）中，即可求出在不同方位角θ情况下测量触发力的大小，其计算结果如下：

方位角在300°～60°间时，

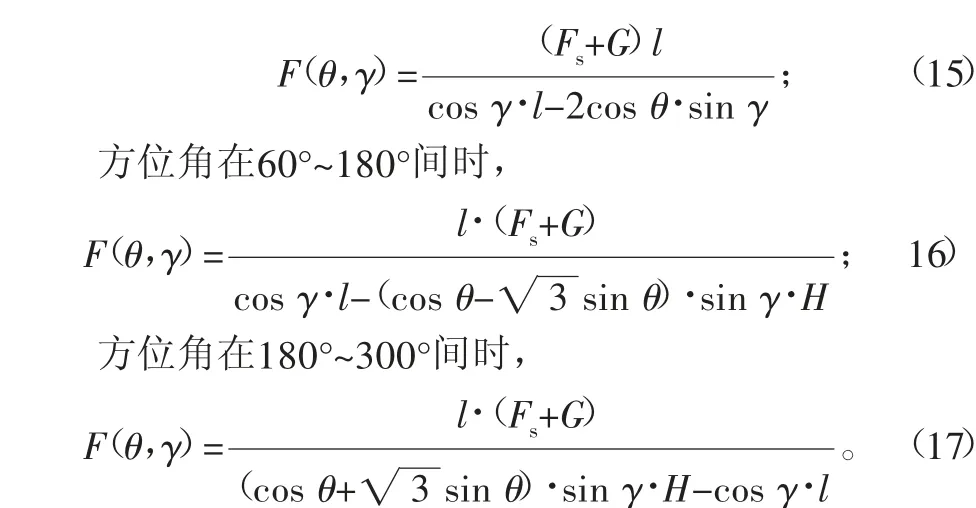
2.3 基于测头预行程误差的补偿方法研究

根据上文对测头预行程P的推导可知，将式（15）、式（16）、式（17）代入式（10），可得出在不同角度区间的测头预行程数学模型。根据非球面零件的测量原理可知，系统记录的坐标为测球球心坐标，用（xQi，yQi）表示，要想得到测头与非球面零件表面接触点坐标，必须在沿接触点法矢方向上对测球半径和测头预行程误差值进行补偿，令测头与非球面零件表面接触点的坐标为（x，y），有：

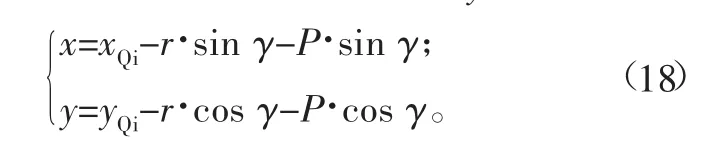
3 实验结果与分析

为了验证在非球面接触测量中触发式测头的预行程误差补偿的有效性，根据非球面零件的加工工艺流程，在完成工件铣磨后，将测头装在机床的主轴上直接检测非球面零件的面形轮廓。测头沿着非球面零件的母线移动寻找待测点，最终可以得到若干个离散的非球面矢高数据点，通过这些数据点就可以得到非球面的一条母线轮廓。

根据前文对预行程误差模型分析，其本质上就是预行程误差与测量触发力的方位角θ、极角γ之间的关系。由于测头自身具有对称性的结构特点，探究方位角对预行程误差的影响时，只需要在完成一条非球面母线测量后，改变方位角继续下一次测量，本实验每次改变10°，一共改变6次即可；而极角就是被测点的斜率，用X轴坐标点代入式（1）即可求出极角值。

本文所测非球面零件理论加工参数如下：曲率C=1/31.788；顶点曲率半径R=31.788；零件口径D=32.4 mm，其中二次曲面系数K=-5.318285，中心厚度为6.5 mm。如图8、图9所示，经实验测得未补偿预行程误差前PV值为5.5924 μm，RMS为1.3614 μm，经过式（18）补偿后PV值为2.3428 μm，RMS为0.3821 μm。为了验证实验结果的准确性，将零件移至Taylor Hobson PGI1240型轮廓仪进行检测，其检测结果为PV=2.1050 μm，RMS=0.2562 μm。经两种检测方式的结果对比，其PV值误差为0.2378 μm，RMS值误差为0.1259 μm。本实验所使用的方法所得结果合理。

经实验证明，本文针对触发式测头在非球面零件面形测量中预行程误差补偿效果明显，且与轮廓仪测量结果误差在0.2 μm左右，故该预行程补偿方法可以应用到实际加工过程中。根据图8、图9可知，在非球面零件测量过程中随着测量斜率的增大，其预行程误差随之增大。

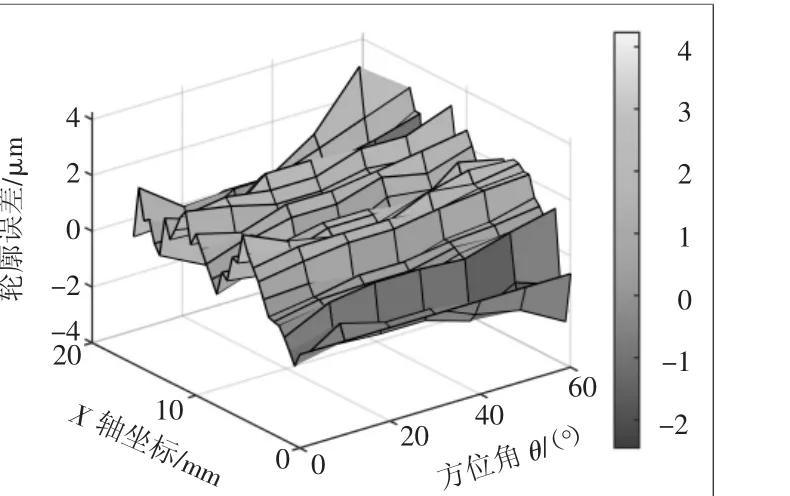
图8 未补偿误差数据图

图9 补偿误差后数据

4 结论

本文通过对影响触发式测头预行程误差的因素进行建模，推导出预行程误差补偿模型，可以提高非球面零件的测量精度。但是该误差还会受到测量速度、测头探针参数和接口响应等因素的影响，为了进一步提升测量精度，还需要更深层次的研究。