大涵道比风扇转子在畸变流场中的三维气动特性研究
2022-02-19蒋聪,刘冕,熊欣
蒋 聪,刘 冕,熊 欣
(中国航空工业集团公司金城南京机电液压工程研究中心,江苏 南京 211106)
进气畸变是导致航空发动机气动稳定性恶化的重要因素之一,亟需探索能高效且准确预判压气机在畸变流场下的性能和稳定性的计算方法[1]。畸变流场通常是不对称的,因此计算域需要以压气机整环为目标,如采用三维非定常的雷诺平均Navier-Stokes方程(以下简称RANS)[2-3],但当前的硬件水平难以承受其数量宏大的网格,所需耗费的时间成本对日常工程设计工作而言十分可观。前人为解决RANS计算量大的情况,提出了彻体力模型[4-6]。
彻体力模型是根据无穷多叶片理论推定的,不再拘泥于叶片的具体结构和形状,将叶片排对流体产生的压升及转向影响简化为分布式彻体力,并将其作为源项代入到三维欧拉(Euler)方程中针对叶片通道内的畸变流场进行求解,很好地表征了其大尺度特征。
彻体力模型无需直接针对叶片力[7]和黏性细节进行耗时较大的计算,大大缩短了计算时长,因此将其应用于工程分析具有较大优势。与以前的二维计算模型不同[8],彻体力模型直接针对三维流动控制方程进行求解,可以更准确地将畸变流场的三维特征反映出来[9]。
本文根据彻体力模型的基本理念,编制出一款可以预测压气机在进气畸变条件下气动特性及稳定性变化的数值计算程序,使用该程序研究了周向畸变流场中大涵道比风扇转子特性,并得出畸变流场的三维特征。
1 计算程序建模
1.1 控制方程
本文使用的控制方程是绝对直角坐标系下具有源项的三维非定常Euler方程:
(1)
式中:t为时间;ρ为气流密度;e为气流总能量;Vx,Vy,Vz分别为沿x,y,z轴的速度;x,y,z分别为3个维度坐标轴;P为气流压力;Fx,Fy,Fz分别为沿x,y,z轴的彻体力;Lu为轮缘功。
1.2 源项构造
彻体力的构造选择在绝对圆柱坐标系下进行,然后依据图1所示的坐标关系演变为直角坐标系下的形式。

图1 彻体力演变
彻体力源项在叶片区域分解为垂直于相对速度V′的非耗散项φ和平行于相对速度V′的耗散项f,得到式(2)~式(4):
(2)
(3)
(4)
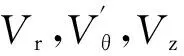

(5)
式中:α为如图2所示角度;Vm为子午速度。
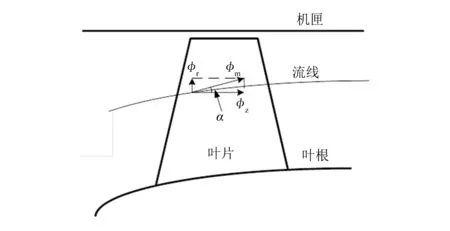
图2 子午面示意图
在式(5)的基础上,最终得到式(6):
(6)
假定子午面网格线为流线,则α可以由网格几何参数求得。如此只要求出式(3)中的|f|以及式(6)中的φθ,再结合三维Euler求解器的瞬时速度场即可求得彻体力源项。
基于轴对称假设及热力学第一、第二定律,Marble提供如下解法求解|f|及φθ:
(7)
(8)
式中:r为半径;m为子午坐标;T为气流静温;s为气流熵。式(7)中∂rVθ/∂m表示叶片区域速度环量沿子午面流线的导数,离散为Δ(rVθ)/Δm,Δ(rVθ)及Δm本质上应该是叶片区子午面每一网格单元的参数。如果假设叶片区任一叶高进出口的速度环量变化量Δ(rVθ)沿叶片进出口的子午面流线线性分布,则Δ(rVθ)及Δm就可以表示为叶片区任一叶高进出口的参数,而式(7)中的剩余变量ρ,Vm,r仍为网格单元的参数。对式(8)中∂s/∂m作相同处理。
根据已知的叶排特性求得叶片进出口的Δ(rVθ)及Δs(气流熵的变化量),并结合三维Euler求解器的瞬时流场,就可以利用式(3)及式(8)求得fr,fθ,fz,再由式(7)求得φθ,继而求出φr,φz,能量方程中的源项Lu=Fθωr,至此得到叶片区域彻体力源项的分布。
Δ(rVθ)及Δs的计算式如下:
Δ(rVθ)=r2Vθ2-r1Vθ1=r2Vz2tanβ2-r1Vθ1
(9)
(10)
而对于转子部件总温比τ*与出气角β2,它们之间有如下关系:
r2Vz2tanβ2-r1Vθ1=U2Vθ2-U1Vθ1=
(11)
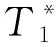
1.3 特性关联
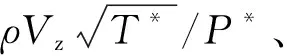
2 总压畸变条件下风扇流场的数值模拟
2.1 计算对象
本文以某大涵道比涡扇发动机的进口风扇转子为算例开展计算与分析,部分参数见表1。

表1 进口风扇转子部分参数
本文计算程序根据流场特性模拟划分的网格如图3所示,周向、径向和轴向的网格单元数分别为60,20和79。沿压气机全环通道生成网格(不含椎体),并以其作为计算域,模拟进气畸变对压气机的影响。由于对于彻体力模型而言,网格密度对计算结果精确性的影响不大[10-11],因此本文所划分的网格密度是完全可行的。叶片的具体形状在彻体力模型计算时无需考虑,因此可以靠两条径向网格线来确定叶片区域的前后缘位置,且周向网格单元对于旋转轴线是对称的。由此可知,计算网格简单且均匀,大大加快了收敛和数值计算的速度。
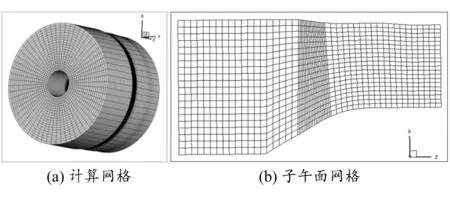
图3 网格单元
2.2 计算程序可靠性对比验证
为验证本文程序的计算准确性,将其计算所得数据与NUMECA计算结果进行对比。特性计算针对均匀进气条件下的风扇开展,在不同背压条件下得出包含总温和总压随折合流量变化的流场特性,对比情况如图4所示。

图4 特性对比
从曲线来看,本程序与NUMECA计算得到的风扇特性结果基本相符,其中最大质量流量点、总温比-流量特性和总压比-流量特性与NUMECA计算结果基本吻合,特性线的趋势也基本一致。
根据以上对比分析结果,可以认为本计算程序采用的计算模型能够对风扇转子特性曲线进行精度较高的预估,并且可以可靠地描绘风扇的相关流场。
2.3 稳态进气条件下畸变流场模拟计算
采用2.1节给出的计算对象,并按表2数据设定畸变条件。
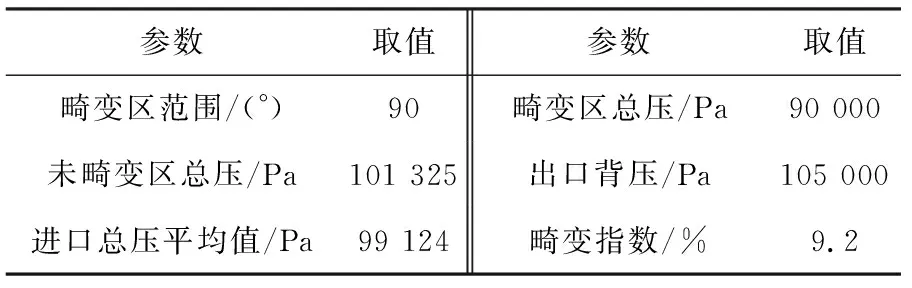
表2 畸变条件
进气总压畸变条件下畸变特性点在均匀进气特性图上的位置如图5所示。
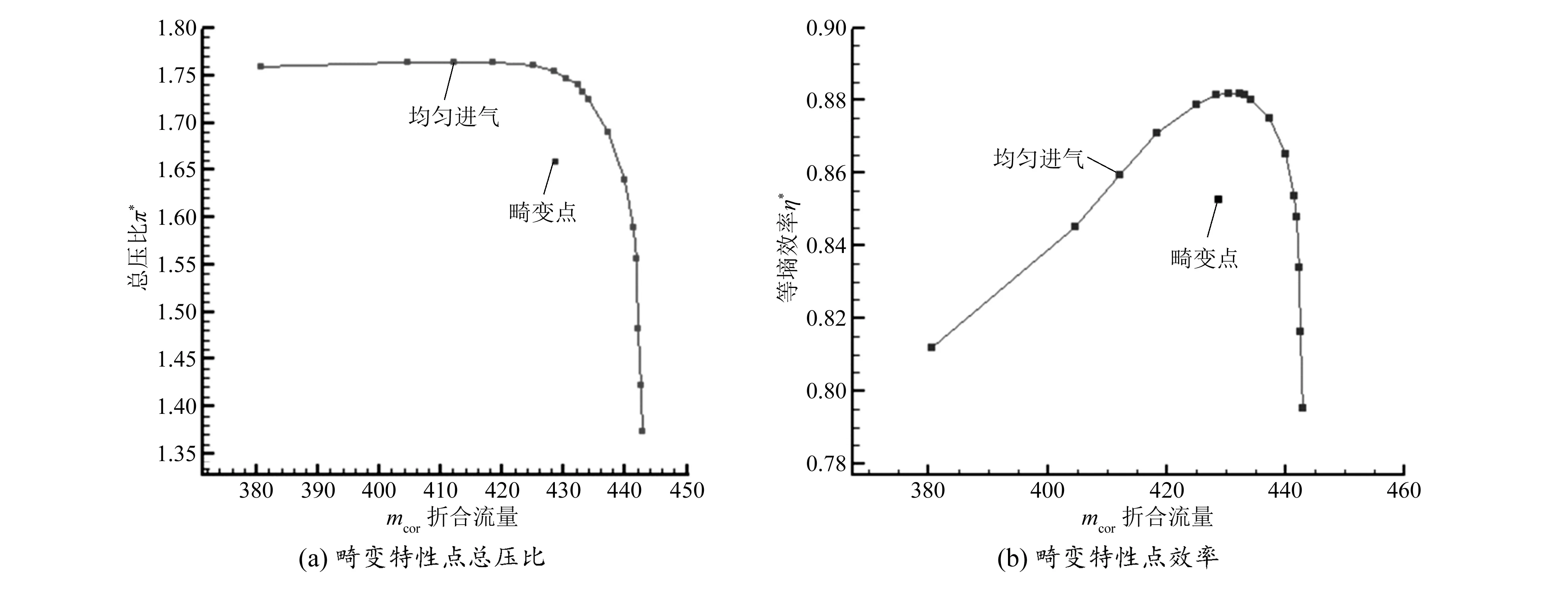
图5 进气畸变特性点
在风扇进口设定范围为90°的畸变区,如图6所示。
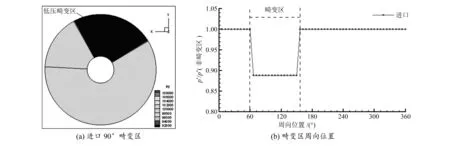
图6 进口总压畸变区设定
经过本文计算程序计算后得出的总压畸变如图7所示,可以清晰地看出畸变流动的强三维特征,且低压区在叶根和叶尖处有明显的相位移动。总压的不均性在经过风扇转子后被削弱了,这是由于低压区经过转子后会产生较高的压升。在叶片尾缘截面上,转子叶片旋出低压畸变区的区域附近出现高压区,沿着叶片旋转方向该高压区逐渐衰减,最低数值出现在转子叶片旋入畸变区时。

图7 总压畸变分布
从图8可知,风扇进口处的总压畸变将在转子叶片尾缘处诱发产生总温畸变,且在畸变区总温最高,产生这种现象的原因是由于在转子进口的周向方向上总压参数不均匀,继而导致不同转子叶片通道内的加功量不同,低总压区域的加功量大且表现在叶片出口就是总温较高。
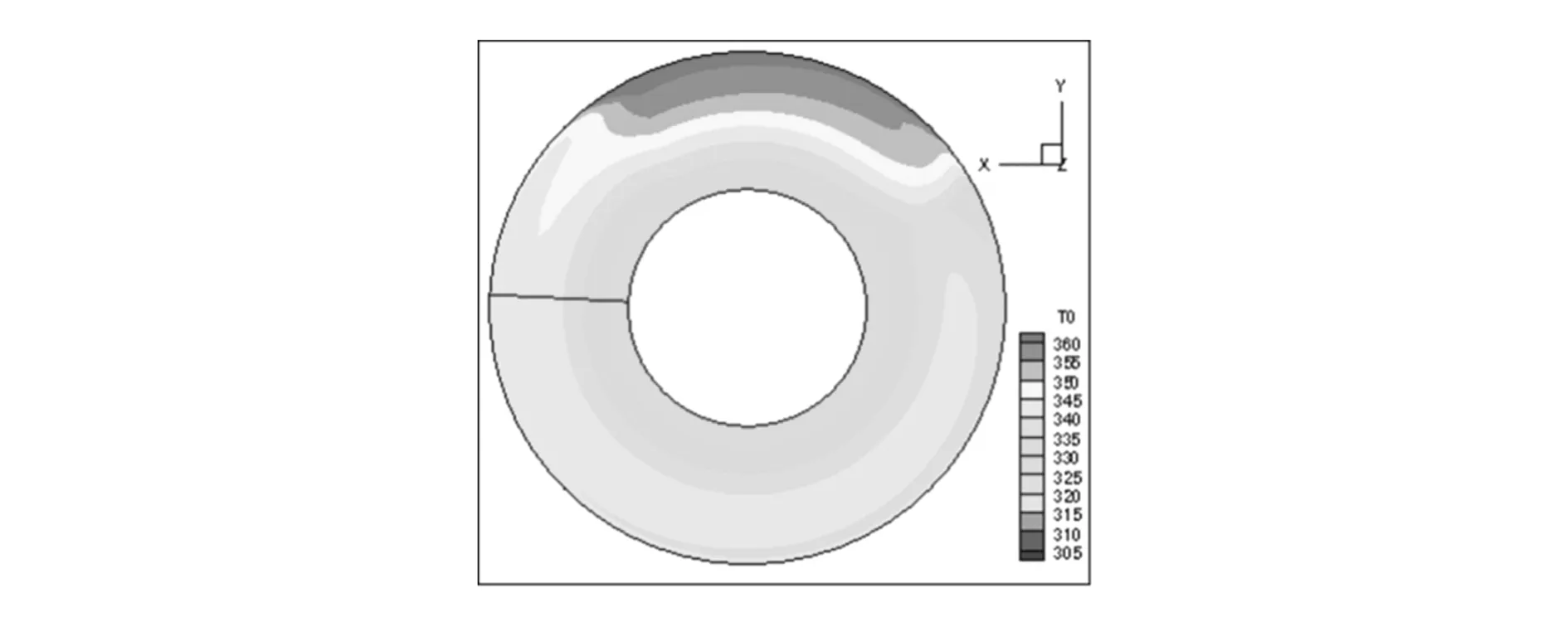
图8 叶片尾缘截面总温畸变分布
3 结束语
本文给出的基于三维彻体力的计算模型具有较高的预估精度,能够较好地刻画出畸变流场流动的大尺度和三维特征,为预测压气机在进气畸变条件下的气动特性提供了一种新的解决方法。但是,目前的研究工作仅通过计算实例来验证模型的准确性,要真正在实践中体现其价值,还需要通过试验结果对比校正,才能对其进行进一步的完善。
