基于模糊评价的规则晶胞骨支架结构优选
2022-02-19武力黄伟关天民刘阁胡鹏
武力,黄伟,关天民,刘阁,胡鹏
(大连交通大学 机械工程学院,辽宁 大连 116028)①
骨缺损问题已经成为临床常见的疾病,危害着患者的身体健康[1].目前临床医学上治疗骨缺损的方法主要有自体骨移植[2]和异体骨移植[3],由于供体来源有限、排异反应等问题,骨组织工程支架的研究得到了人们的广泛关注.骨组织工程支架内部的孔隙率、孔径大小、比表面积和连通性等结构参数对骨的重建有着重要的影响.因此,构建科学合理的骨组织工程支架对于骨组织的重建有着重要的意义.
理想的支架结构应该是高度多孔的,具有相互联通的结构,以允许细胞、营养物质和代谢废物的迁移,同时还应具有较大的比表面积以促进细胞的黏附、增殖和分化[4],所以设计出与天然骨组织内部结构相似的支架结构是骨组织工程中重要的研究方向.目前关于骨组织工程支架的研究主要集中在对支架结构的设计[5-7],力学性能分析[8-10]以及生物材料研究[11-13]等方面.对于设计的支架,选用的材料其综合性能是否符合临床移植对支架的要求,目前尚无标准的综合评价体系.Bian[14]等设计了一种仿生双相支架并对其性能进行了评价.Kim[11]等选用聚己内酯和β-磷酸三钙制作了多孔支架,并对其生物性能进行了评价.Seol[15]等进行了壳聚糖支架体外培养试验,但并为对支架性能进行评价.所以对于支架综合性能的评价需要研究相关的评价体系,以用于骨支架综合性能的评价.
本文为了对支架的结构性能进行研究,利用规则几何体圆柱、球体以及立方体进行了三维结构组织工程骨支架的构建,并通过模糊理论对设计的骨组织支架进行了综合性能的评价.
1 规则晶胞骨支架设计
在组织工程骨支架的设计中充分考虑孔隙率、弹性模量以及比表面积,设计出与天然骨组织结构相似的支架结构一直是困扰骨组织工程领域的一大难题.而基于规则几何体的骨组织工程支架设计是一种简单快捷的方法,通过一些简单的规则几何体进行阵列与组合,不仅能够设计出具有空间互联通孔隙结构的支架,而且可以通过对规则几何体尺寸的修改实现对设计结构孔隙率、弹性模量等的控制.
立方体、球体、圆柱体是我们常见的规则晶胞,将直径大小不同的两个球体进行布尔减可以得到一个空心球壳,然后用两两垂直正交的三组平行平面对其进行裁剪即可得到空间互联通孔隙结构的球体晶胞;将三个空心圆柱两两垂直相交即可得到空间互联通孔隙结构的圆柱体晶胞;将规则立方体与空间两两正交的三个矩形进行布尔减即可得到空间互联通孔隙结构的立方体晶胞.
应用三维建模软件对以上设计晶胞进行建模,并且将所得模型分别沿x、y、z轴阵列可以得到立方体结构、球形结构与圆柱结构,如图1所示.由于实际中对不同大小结构支架的需求,因此对以上支架结构分别取三种不同尺寸范围(10.2 mm×10.2 mm×10.2 mm、12.3 mm×12.3 mm×12.3 mm、14.4 mm×14.4 mm×14.4 mm)进行分析,此外考虑到支架不同壁厚对支架孔隙结构及力学性能的影响,对不同尺寸范围的支架分别取壁厚为0.4,0.6,0.8 mm,共27种尺寸结构以研究支架的综合性能.以上方法所得支架结构不仅具有相互联通的孔隙结构,而且具有一定的力学性能,可以为细胞的黏附、增殖与分化提供良好的环境,同时可通过对三种结构几何特征的调整得到不同孔径、不同孔隙率的支架结构,是一种简单快捷的支架设计方法.

(a)立方体结构 (b)圆柱结构 (c)球形结构图1 支架结构
2 骨支架性能指标及参数测量
制作组织工程骨支架的目的是引导骨细胞的生长、分化与增殖,要求支架能够为细胞生长提供一定的空间环境以及营养物质.对制作的骨支架进行相关性能的测量及评价是考察骨支架可靠性的重要一步.组织工程骨支架要求其有足够的孔隙率,同时还要保持一定的力学强度以及相应的生物指标,因此以孔隙率、弹性模量、黏附率为目标可以对所设计三种结构组织工程骨支架的综合性能进行较全面的评价.
2.1 孔隙率
孔隙率是指支架孔隙部分体积与总体积的比值,是描述支架内部孔隙多少的量,当支架孔隙率较大时,会对细胞的生长起到促进作用.研究表明,孔隙率在60%~90%之间的骨支架,能够很好地模拟松质骨的内部结构,有利于细胞的黏附、增殖与分化.因此,孔隙率是描述支架性能的重要指标,其计算公式见式(1)
(1)
式中:η为孔隙率;Vp为支架孔隙体积;Vz为支架总体积Vs为支架实体部分体积.
2.2 弹性模量测量
支架结构的弹性模量是衡量其变形难易程度的一项重要指标,弹性模量的值越大,即支架发生变形所需的应力越大.采用有限元分析法得出支架最大应力和应变,从而间接计算出支架的弹性模量.
2.2.1 支架结构的有限元分析
以单位体积(14.4 mm×14.4 mm×14.4 mm)内,壁厚0.8 mm的三种支架结构为例,取标准青少年体重70 kg为研究对象,对其上表面施加压力,下表面固定,分析结果如图2发现球形结构在薄壁处产生应力集中, 所受最大应力、 最大应变都最大,为94.6 MPa,3.98×10-2mm/mm;其次是立方体结构在竖直棱柱处产生应力集中,所受最大应力、最大应变为85.9 MPa,1.30×10-2mm/mm;圆柱体结构应力分布相对集中,产生的最大应力和最大应变都最小,为75.7 MPa,9.71×10-3mm/mm.

(a) 立方体结构
2.2.2 支架结构的弹性模量
骨组织工程支架作为植入人体内进行承重的部分,其必须具有一定的弹性模量,以防止支架在受力时发生变形,产生破坏.对于不同的支架结构,当支架受到外力作用时,在弹性变形阶段,其弹性模量的计算公式见式(2)
E=(F/S)/ε
(2)
式中:F为支架所受外力(N);S为支架的受力表面积(mm2);ε为支架所受的最大等效应变(mm/mm).
2.3 黏附率
细胞在支架上的黏附率是指细胞接种到支架上在支架表面的黏附情况,通常来说,支架的比表面积越大,其吸附能力就越强,能够为细胞的黏附、增殖及分化提供更大的接触表面,有效提高细胞的黏附率,促进骨组织的生成.因此,在不考虑支架材料及表面粗糙度时可以用支架的比表面积近似表示支架的黏附率,比表面积是对组织工程支架内部空隙空间的描述量,也称相对表面积或表面体积比,其计算公式见式(3)
(3)
式中:δ为支架比表面积;Sp为孔隙表面积;Vs为实体体积.
2.4 不同支架结构性能参数测量结果
对不同支架结构进行性能指标参数测试,得到分析计算结果如表1所示.
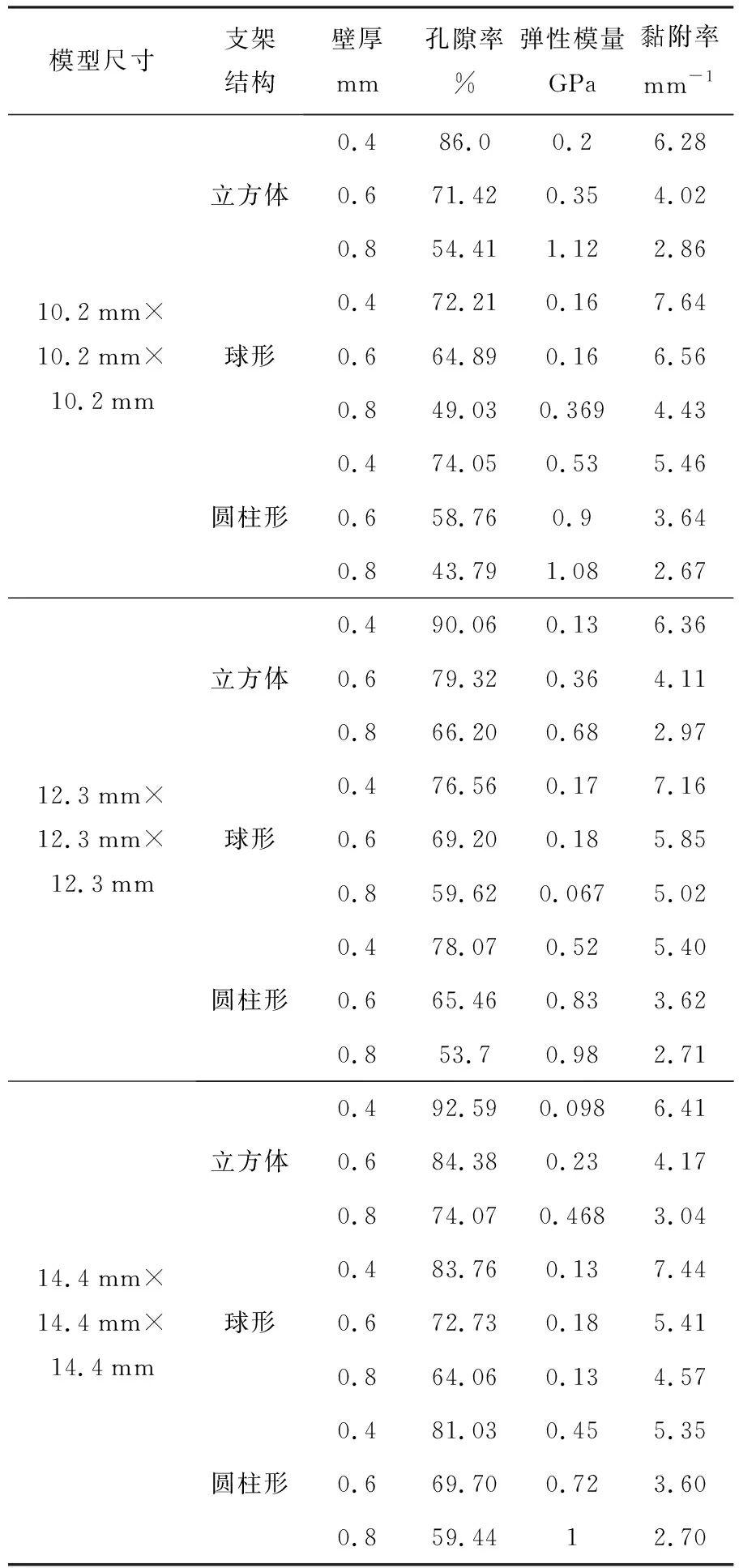
表1 不同结构支架的性能参数
3 支架结构性能的模糊评价
采用模糊综合评价法[16],对设计的三种骨支架结构的孔隙率、弹性模量、黏附率的综合性能进行评价,优选出最优的骨支架结构.
(1)评价指标的构建
根据支架的性能指标要求,模糊评价指标选定为孔隙率、弹性模量及黏附率.
(2)确定支架的因素集U和评语集V
根据影响支架力学性能的几个评价因素得出因素集U为U1:孔隙率、U2:弹性模量、U3:黏附率;
评价集V按照10分值进行评定,V={0-6(差);6-7(一般);7-8(中等);8-9(良好);9-10(优秀)}.
(3)评价方法
为了确定各性能指标的重要程度,采用专家法进行对各指标的重要程度进行确定,其中1为重要性最高的性能指标,2为重要性次之的性能指标,3为3项性能指标中重要性最差的指标.为了使得到的结果更有力,选取了在组织工程领域与生物医学领域具有较高权威性的15名专家和教授进行各指标重要性的咨询,得到表2的15份调查结果.

表2 调查结果统计表
(4)性能得分优先统计表
按照每个参与调查专家的结果进行优先得分表3的制作,其可以用一个Ak=[aij]3×3的矩阵进行表示,当aij=1 时,即参与调查的专家认为第i个因素的重要性要大于第j个因素的重要性,当aij=0 时,即参与调查的专家认为第j个因数的重要性要大于第i个因素的重要性.

表3 优先得分统计表
(5)定义级差
令amax=1 ,amin=0.1
计算级差d
由因素重要程度系数计算公式:
得a1=1,a2=0.1,a3=0.450;其中∑Ai为得分矩阵A各行的累加.
由计算结果的重要程度模糊向量A=(1,0.1,0.450)
规范化得A=(0.908,0.090,0.408)
(6)性能等级评价表
将影响支架力学性能的因素进行优良性等级评价,得到性能等级评价如表4所示.
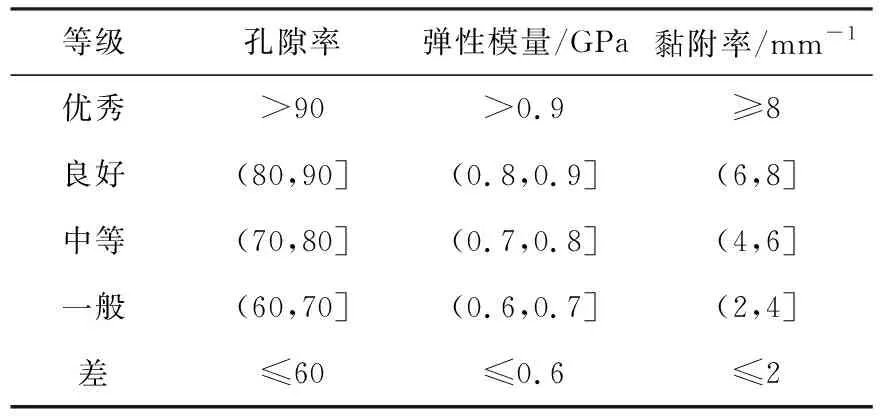
表4 性能等级评价表
(7)构建评价矩阵
由上表的性能评价指标,对仿真结果及孔隙率进行统计,得到表5所示立方体、球形、圆柱形结构的评级矩阵R.
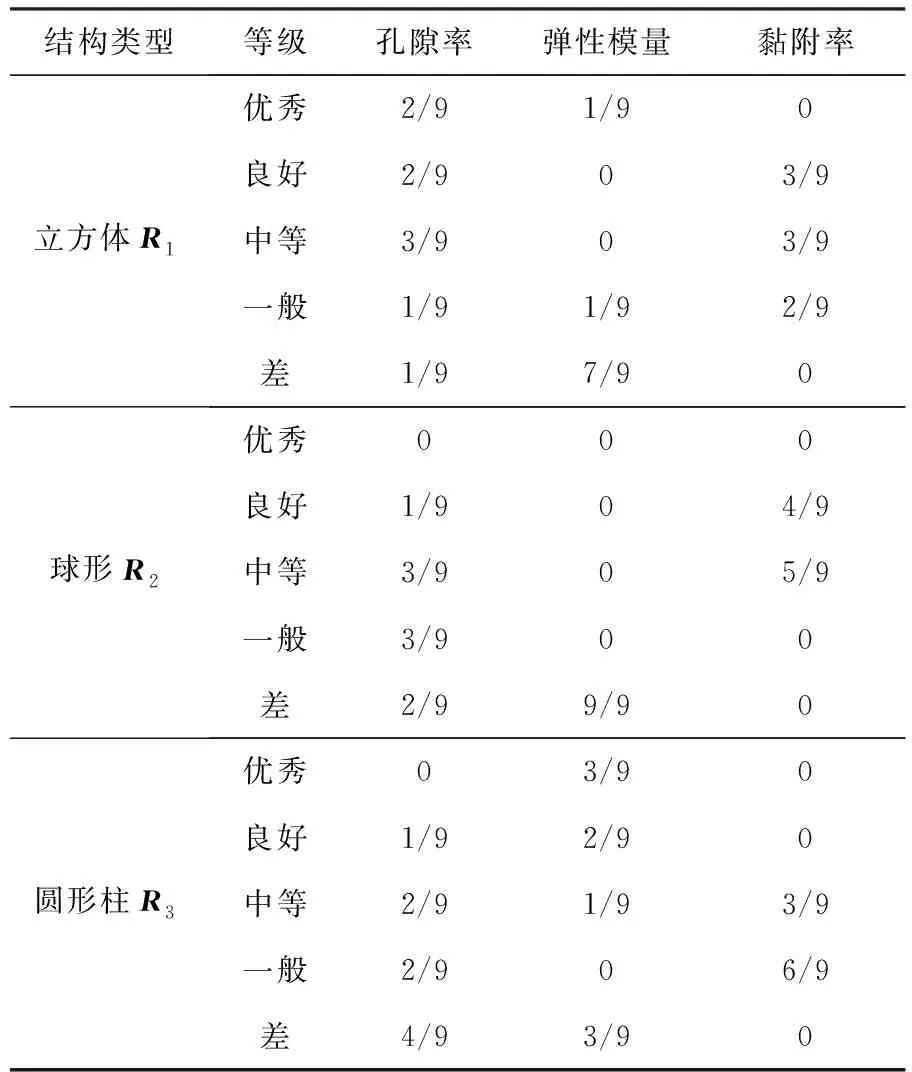
表5 各结构评价矩阵表
(8)综合评价
将因素集U上的模糊子集A通过模糊关系R变换为评价集V上的模糊集,即综合评价的等级模糊子集B,
B=A·R=(b1b2b3b4)
其中,A为权重集
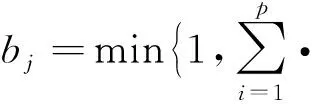
min(ai,rij)},j=1,2,…,m;bj表示某个被评价的支架结构性能为等级Vj的隶属度,即:给每一等级一个等级分,如优秀(100分),良好(75分),一般(50分),差(25分),再求其加权和得出综合分,如表6所示.

表6 综合评价分级权重表
由表6可知,立方体结构支架的性能要优于球形和圆柱形支架机构,因此,采取立方体结构进行骨组织工程支架的设计.
4 结论
(1)以规则几何体为理论基础,设计了三种规则晶胞的骨支架结构,通过对所设计的单个晶胞结构进行阵列得到了最终的三种骨支架结构,分别是立方体结构、球形结构及圆柱结构;
(2)提出了骨支架性能的评价标准和测量指标,通过理论计算方法及仿真分析结果对骨支架的孔隙率、弹性模量及黏附率三种性能进行了测量,得出各支架结构的孔隙率大小、弹性模量参数及黏附率参数;
(3)应用模糊评价法对三种不同结构支架的性能进行了评价,选取了孔隙率、弹性模量及黏附率为性能评价指标,采用不均衡平均模型算子对模糊评价向量和评价矩阵进行运算,分析得出立方体支架的综合性能最优,为骨组织工程支架的设计及结构性能评价提供了参考.
