考虑静动态多目标地铁车座椅拓扑优化设计研究

李娅娜，孟迪

(大连交通大学 机车车辆工程学院，辽宁 大连 116028)①

近几十年，拓扑优化方法被广泛应用到航空航天、材料、车辆、机械等诸多领域.单目标的拓扑优化很难解决实际结构中大量存在着的多目标优化问题，并且结构的受力过程往往比较复杂，一般是在多种工况下进行工作，在定义目标函数时，权重系数的分配在优化设计中占据比较重要的地位，它反映目标的相对重要性涉及优化目标的分配和目标函数的评价方向，如果设置合理，则可以达到理想的优化效果，反之可能达不到预期的效果甚至出现失误.从目前国内外学者的研究状况来看，大多数结构拓扑优化正在从单目标、单工况拓扑优化的问题向多目标、多工况优化问题转变，并且确定多工况权重系数的方法不再单一.目前，在众多领域许多学者提出了不同的拓扑优化方案，周智等[1]提出了一种以最小化柔度为单一的目标，多工况折衷规划法对汽车前轴进行结构轻量化设计；杨森等[2]以加权应变能最小为目标，根据经验对典型工况设置权重，对商用车变速器壳体进行了拓扑优化设计研究；高云凯等[3]通过正交试验得到各子工况最优权重系数组合，以加权柔度为目标函数，约束拓扑空间的质量分数，进行多工况拓扑结构优化；罗震等[4]根据灰色理论建立了解决多工况问题的灰色-折衷规划模型，减少了主观因素对确定各工况权系数的干扰；秦欣等[5]基于熵权法确定各个评价指标所占权重，对汽车进气歧管进行了多目标优化；扶原放等[6]基于层次分析法以车身多工况权重刚度最大化为优化目标，建立了微型电动车车身结构多刚度拓扑优化模型；袁林等[7]考虑碰撞工况，采用层次分析法确定静态多工况下的最优权重系数，对电动汽车电池箱进行了多目标拓扑优化设计；康元春[8]同时考虑货车车架静态动态性能构建了多目标优化函数，并利用层次分析法确定目标函数中各工况的权重系数；兰凤崇等[9]定义了在实际行驶工况下综合考虑车身结构静态刚度和动态振动频率的目标函数，通过对比3种优化方法，获得了每种工况的最佳权重系数，完成了综合目标优化设计.但这些研究都很少同时考虑多目标、多工况以及使用多种方法确定权重系数的拓扑结构优化模型，尤其在铁路车辆结构中的应用就更少了.

本文基于SIMP密度函数插值模型，使用正交试验设计法、灰色关联度法、熵权法和层次分析法4种不同方法确定目标函数中的权重系数，实现不同优化方法在地铁车座椅模型多工况刚度和动态固有频率的多目标拓扑优化研究中的应用.

1 综合目标拓扑优化

1.1 多目标拓扑优化方法的概述

对于非凸优化问题来说，线性加权法和把多目标转化为单目标优化问题来求解的方法不能确保得到全部的帕雷托最优解[10]，而折衷规划法可以很好地解决该问题.确定多工况下目标函数的过程中，通常不同工况权重系数是设计者通过工况重要程度给出一个经验值，但是通过经验给出的权重系数往往受主观因素的干扰，无法保证精确程度；当工况数量较多时，无法合理地对众多工况做出判断给出各工况的权重系数[9]，为了解决该问题本文采用正交试验设计法，灰色关联度法，熵权法和层次分析法4种方法确定目标函数中的权重系数.建立带有权重系数并综合考虑静态多工况刚度和动态固有频率的多工况拓扑优化模型，优化设计分析流程如图1所示.

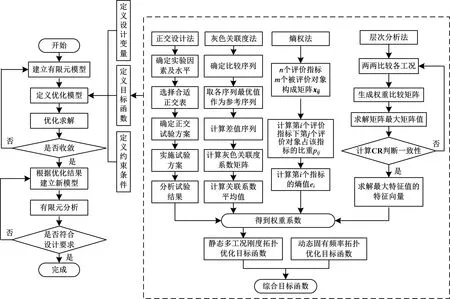
图1 基于不同方法确定权重系数的结构拓扑优化流程

1.2 多目标拓扑优化目标函数的确定

多刚度拓扑优化问题通常是将刚度最大问题转化为柔度最小问题，即单元应变能最小，本文运用折衷规划法以座椅结构柔度的最小化作为目标优化静态刚度.动态固有频率拓扑优化是最大化低阶的前几阶重要频率，本文采用平均频率公式来建立固有频率拓扑优化的目标函数：

(1)

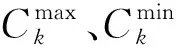
1.3 拓扑优化目标权重系数方法的确定

(1)正交试验设计法

正交试验设计分为试验设计与数据处理两部分[11].由正交设计表可获得用于试验的方案，对试验结果进行计算分析，根据极差值由小到大选择出最优组合，经过归一化处理得到最终权重系数.

(2)灰色关联分析法

最优解参考序列是通过数据整理得到，关联分析各因素的比较序列与参考序列，利用灰色关联度，判断各因素与最优解之间的关联程度，从而给出该因素的权重系数[12].

(3)熵权法

熵权法的构建过程包括样本选择、目标选择、计算权重三个部分.首先采用归一化方法将原始指标矩阵标准化得到标准化矩阵，定义第i个指标的熵之后，可以得到第i个指标的熵权.

(4)层次分析法

根据各个工况的相对重要程度，建立权重比较矩阵，求解矩阵的最大特征值并计算矩阵的一致性判断值[13].若符合一致性指标，则最大特征值对应的特征向量即为所求的系数矩阵，归一化处理后得到对应的权重系数.

2 地铁车座椅模型的建立

2.1 有限元模型的建立

某地铁车二人座椅主要由座椅支架、背部骨架及座椅椅面组成，材料有铝板5083-H112和不锈钢06Cr19Ni10两种，二人座椅结构有限元模型采用任意四节点薄壳单元，单元总数32 469，节点总数31 205，模型重量43.73 kg.位移约束二个支架及端部支架的螺栓孔位置区域，位移约束：x=0，y=0，z=0,三维有限元模型如图2所示.二人座椅每个座椅承受100 kg的载荷，二人座椅共承受200 kg的载荷，均布在椅面上，加载面积为300×1 173 mm2，并考虑三个方向的加速度，工况如表1所示.

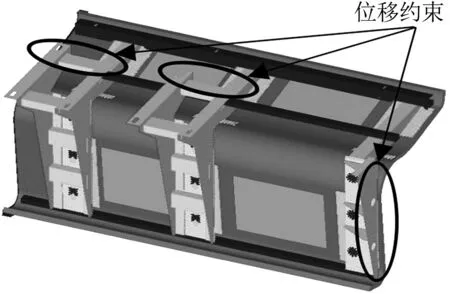
图2 二人座椅有限元模型及位移约束示意图

表1 二人座椅强度分析工况汇总

2.2 拓扑优化模型的建立

本文对地铁座椅进行拓扑优化设计，以原座椅模型结构为基础，综合考虑本次优化设计需求，优化模型描述如下：

(1)优化目标：各工况静态柔度值最小及动态低阶频率最大；

(2)约束条件：以体积分数30%作为约束条件；

(3)设计变量：座椅支架，座椅椅面，座椅背部骨架单元相对密度.

2.3 权重系数的计算

一般来说，静态刚度和动态频率目标是一组相互矛盾的目标函数，当权重分配相差较大，刚度函数和频率函数不一定能够同时得到最优解.出于这种考虑，在多目标拓扑优化综合目标函数中，取刚度目标函数的权重系数0.6，频率目标函数的权重系数为0.4.

本文对工况选用的是三因素三水平的正交试验，每一个工况即每种因素定为3个水平值，所取的水平见表2所示，所取的正交表应为 L9(33)，通过赋值与归一化处理得到最终实验的9组方案，依次进行拓扑优化.

表2 各因素水平表

分别将各工况的柔度作为灰色关联度法中的比较序列，以及构成熵权法中的原始指标矩阵.依照比较矩阵重要性参数定义水平表把所有工况进行两两对比，确定其相对重要程度[14]，得到层次分析法中的权重比较矩阵：

(2)

利用正交试验设计法，灰色关联度法，熵权法和层次分析法计算得到不同方法对应的地铁车二人座椅三个工况的权重系数如表3所示.

表3 不同方法对应的权重系数

3 优化结果计算与分析

由于权重系数的不同，综合目标函数存在较大的差异，本文提出使用四种方法确定各个工况的权重系数，为了比较四种方法的优劣，将四种方法得到的权重系数分别进行拓扑优化，各目标函数的最终优化结果如表4所示.

表4 不同方法对应目标函数的优化结果

四种方法建立的目标函数经过迭代后收敛，实现了多工况柔度最小化和低阶频率最大化的目标.优化后的各工况柔度达到最小值，在各工况柔度优化值对比中，方法4的柔度优化值比其他方法低，这表明每个工况刚度得到很大的提高，刚度特性变得更好；优化后结构低阶频率也都得到了提高，方法4的低阶频率值最高，具有更好的振动特性.

采用层次分析法建立的拓扑优化模型，对地铁车座椅进行多目标拓扑优化计算.图3给出优化后的密度分布情况.

图3 层次分析法优化后的密度云图

从密度云图可以看出，座椅靠背部分密度值较小，可以在该处适当减少材料的分布，将座椅靠背处较少承受载荷的部分删除,留椭圆形镂空，进行二次设计后座椅柔度和频率值与原模型对比结果如表5所示，由表5可知，优化后地铁座椅各工况柔度值均有所降低，频率值有所增大，有较明显的优化效果.

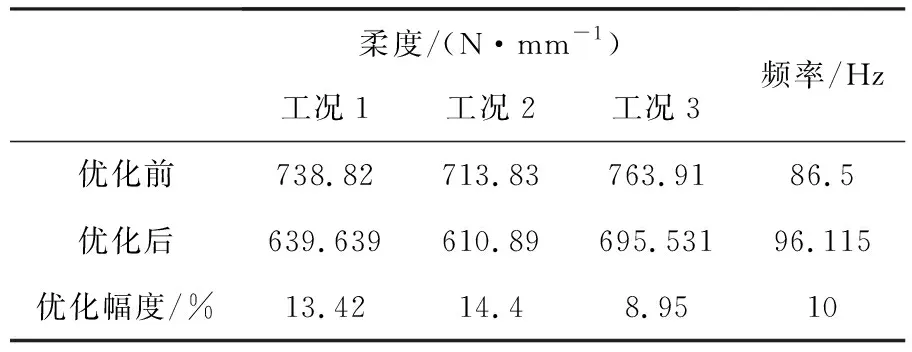
表5 优化前后地铁车座椅柔度和频率值对比

4 结论

(1)基于变密度法，考虑静态刚度和动态频率多目标及不同权重系数对不同工况的重要程度的影响建立了综合目标函数拓扑优化方法;

(2)通过正交试验设计法，灰色关联度法，熵权法和层次分析法，给出了地铁座椅目标函数中不同的权重系数，减少了人为主观因素造成的权重系数偏差，获得了更加合理的拓扑优化模型;

(3)采用层次分析法建立的拓扑优化模型，根据密度云图进行优化设计后座椅工况1柔度降低13.42%，工况2柔度降低14.4%，工况3柔度降低8.95%，频率值提高10%，优化后地铁座椅各工况柔度值均有所降低，频率值有所增大，优化效果较明显;

(4)通过分析优化结果可以看出四种模型均可以实现多工况多目标的拓扑优化，综合对比各工况柔度值和频率值变化，由层次分析法确定的目标函数方法拓扑优化结果优于其他三种方法.因此，在结构拓扑优化设计中，在刚度特性不减弱的情况下，所设计的结构有更好的动态频率特性，从而为今后优化铁路车辆结构提供了有益参考.