韦氏摆的弹性力学分析:圆柱螺旋弹簧模型的特色推导与验证
2022-02-18刘天恒曹博星张福林
刘天恒,曹博星,张福林
(天津大学 理学院,天津 300350)
韦氏摆又称威尔伯福斯摆,由竖直悬挂的圆柱螺旋弹簧和固连在弹簧末端的物块组成.物块有两个广义坐标:在竖直方向偏离平衡位置的位移z,绕竖直轴偏离平衡位置的角位移φ,如图1所示.系统振动时,若系统参量处于一定范围,可以明显地观察到物块的平动动能和转动动能发生周期性转化.

图1 韦氏摆示意图[3]
韦氏摆是中学、大学物理教学中经典的演示实验,目前,文献[1]、[2]给出了系统唯象的拉格朗日函数模型,描述了耦合的线性特征,测量了唯象系数和耦合现象的拍频周期,基本验证了唯象理论的正确性.
但是,前述模型的唯象参数并非是通过系统的物理模型推导得出.因此,本文建立了圆柱螺旋弹簧的弹性力学模型,分析了弹簧钢材料参数(杨氏模量,剪切模量)和系统几何参量(弹簧线径,轴半径,物块质量等)对弹性势能的影响,给出了圆柱螺旋弹簧弹性势能的解析解,得到了由基本参量描述的唯象参数.本文的弹性力学分析可以简洁且精确地描述圆柱螺旋弹簧的力学性质,同时,其方法也可以推广应用于其他均质弹簧的计算.
1 唯象模型
本节分析韦氏摆的唯象模型,在小振动的情况下,系统的拉格朗日函数可表示为[1]
(1)
其中K是弹簧的劲度系数,D是弹簧的扭转系数,λ是系统的能量与两个广义坐标的耦合相关的系数,m、J是与系统动能相关的唯象系数,它们分别是系统竖直方向运动的等效质量和水平方向转动的等效转动惯量.根据参考文献[2],系统的简正坐标为
(2)
其中
系统的两个特征频率Ω1、Ω2分别为
(3)
为了更清楚地看到系统的能量转化现象,取Γ为系统的两个特征频率差值的一半,即Ω1=Ω+Γ,Ω2=Ω-Γ,调幅函数为
(4)
系统的运动方程为
(5)
其中,A1、A2是系统简正坐标的振幅,相位为
根据式(5),若Γ<<Ω,系统在z、φ方向的振动可视为是一个频率为Ω的快振动被函数Bz(t)、Cφ(t)以较慢的频率2Γ调幅的结果,即为耦合现象.
2 弹性力学分析
拉格朗日函数中的K、D、λ取决于弹簧的材料参量和几何参量.下文通过弹性力学分析,给出它们的解析解.
2.1 弹性力学模型
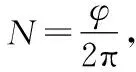
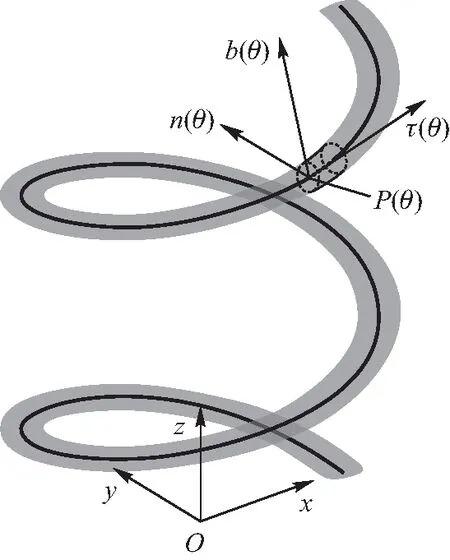
图2 弹簧模型示意图
如图1所示,取系统处在平衡位置时,弹簧轴线的最低点所在的水平面,与弹簧竖直轴线相交的点为原点O, 构造Oxyz直角坐标系,其中x轴的正方向指向弹簧轴线的最低点,z轴的正方向竖直向上(如图2),并在该坐标系中构造参数方程为
(6)
的圆柱螺旋线(图2中黑实线),θ是用以确定圆柱螺旋线上某一点的变量,图中仅标注出了[0,φ]中的一个点作为示意.记曲线上坐标为(x(θ),y(θ),z(θ))的点为P(θ),以其为原点,建立自然坐标系.en(θ)为曲线在P(θ)点法向单位矢量;eτ(θ)为曲线在P(θ)点的切向单位矢量;eb(θ)为曲线在P(θ)点的副法向单位矢量.
en=(-cosθ,-sinθ,0),
将杨氏模量为Y,剪切模量为G的材料均匀填充在空间区域(图2阴影区域),有
(7)
即可得到几何参量如上的圆柱螺旋弹簧.假设弹簧的材料是线性的,那么悬挂物块后处于平衡位置的弹簧与相同尺寸的空载弹簧是等价的,下文以该模型分析在平衡位置的弹簧是合理的.
记k为式(6)所描述的曲线的曲率,t为曲线的挠率,L为曲线的长度.显然,弹簧的长度为L.对照广义坐标的定义,若取z轴为竖直方向,则z=-ΔH,φ=Δφ.当物块的广义坐标变化时,弹簧中的一段弹簧丝会产生以下三种基本的形变:垂直轴线的弯折,沿轴线的拉伸压缩,绕轴线的扭转.它们与材料的主应变和剪应变有关.以下将讨论这两种应变对弹性势能的贡献.
在下文的弹性力学分析中,假设系统在运动过程中始终满足条件:
(8)
其中ρm为金属材料密度.系统参数满足式(8),意味着弹簧丝中的一维应力波波长远大于弹簧丝长度,可认为此时应力和应变沿轴线方向均匀分布,弹簧丝轴线始终为圆柱螺旋线.
2.2 材料剪应变的应变能

图3 应变能计算图解
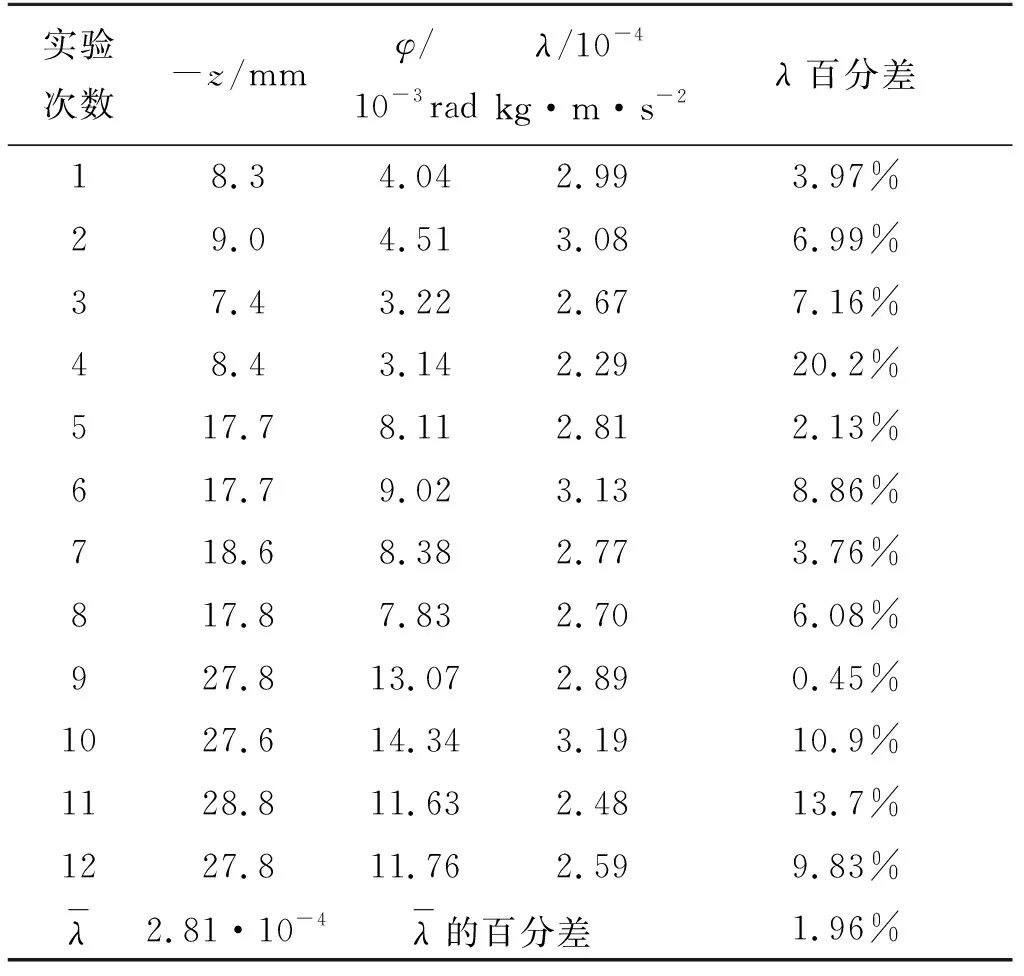
本节讨论剪应变的应变能对弹性势能的贡献.如图3所示,任取一个θ∈(0,φ),考虑图2中一段长度为l(l< en(θ′)=en(θ) (9) eb(θ′)=eb(θ) (10) 同时,根据应变的对称性,en(θ)、eb(θ)所在的坐标平面内的剪应变方向可认为是沿以O(θ)为圆心的圆周分布的,所以,对于被各en(θ)、eb(θ)所在平面截得的面积元dSθ的坐标都为en(θ)-eb(θ)的柱形微元[如图3所示,en是en(θ)轴的坐标值,eb是eb(θ)轴的坐标值],其剪应力大小可认为仅与微元自身的参量和参量变化有关,可作为计算应变能的独立微元.微元的长度为 (11) ln=l(1-ken) (12) 为推导简便,下文推导仅采用近似式(12),其精度已经足够高. 挠率的绝对值度量了曲线上邻近两点的副法向量之间的夹角对曲线弧长的变化率,如图3所示,考虑式(9)、、式(10),弹簧参数的应变等效于该段弹簧丝扭转Δ(tl)的角度.认为应力沿轴线均匀分布,弹簧丝轴线始终呈圆柱螺旋线.忽略高阶小量,微元对应的应变能为 (13) 单位长度弹簧丝剪应变的应变能为 (14) 本节讨论主应变的应变能对弹性势能的贡献.如图3所示,考虑图2中一段长度为l(l< 认为应力沿轴线均匀分布,弹簧丝轴线始终呈圆柱螺旋线,微元对应的应变能为 (15) 注意到en(θ′)=en(θ),单位长度弹簧丝主应变的应变能与参量应变量的关系为 (16) 积分区域如上节,有 本节给出弹簧弹性势能的解析解,根据参数方程(6),系统参量的几何约束关系为 (φR)2+H2=L2 (17) (18) (19) (20) (21) 联立式(12)、式(17)、式(18)、式(19)、式(20),以弹簧丝长度的应变量的解作为该约束关系,结果为 (22) 式(21)意味着,如果只考虑主应变,那么弹簧丝内部必定存在一个主应力为0的范围,称为中性层,其内部Δln=0,这一范围可表示为 (23) 根据上文分析,剪应力和主应力方向正交,假定构成弹簧丝的金属材料是线性的,则弹性势能E为剪应变和主应变产生的应变能的总和. E=(EG+EY)L= (24) (25) 舍去三个数量级以上的小量.注意到广义坐标z、φ就是-ΔH、Δφ,系统势能: (26) 上式中各参量取悬挂物块后系统处在平衡位置时的值,拉格朗日函数可得.考虑式(22),可知弹簧丝长度L的应变完全可略. (27) (28) 其中m1是物块质量,m2是弹簧质量,J0是物块的转动惯量. 唯象系数K、D、λ的解析解为: (29) (30) (31) 其中K为弹簧的劲度系数,D为弹簧的扭转系数,λ是弹簧耦合的相关系数,定量描述了应变能关于拉伸形变、扭转形变的耦合强度.考虑小振动的对称性,上述解析解中的参量取悬挂物块后系统处在平衡位置时的值. 在圆柱螺旋弹簧的弹簧丝轴线上,挠率、曲率处处相等,它们与线径d的乘积相对1来说都为小量.这一几何结构的高度对称性使系统的力学性质也表现出高度的对称性.即系统做小振动时,剪应变的应变能几乎完全受挠率的应变影响,主应变的应变能几乎完全受曲率的应变影响,剪变模量G、杨氏模量Y在唯象系数式(29)、式(30)、式(31)中对称的数学地位也表现出了这一高度的对称性. 文献[1]、[2]验证了韦氏摆的唯象理论和动力学理论,故本文只需验证弹簧理论的正确性.文献[7]给出了K和D的解析解,它们与上文的式(29)和式(30)仅相差高阶小量,这一小量在本文的实验条件式(25)下已远小于实验的系统误差.所以,本文只验证λ的解析解式(31)的正确性. 若系统在φ这一自由度上不受外力矩,即 (32) 系统处在平衡位置时,参数满足 (33) 条件式(32)可通过仅在弹簧下端悬挂重物来简单实现.测得特定弹簧发生位移z时平衡位置的角位移φ,再通过式(30)计算D(各参数根据厂家所给出的参数计算),就可以根据式(33)计算λ,将这一结果与理论值式(31)比较,即可检验λ的正确性. (a)实验支架示意图 (b)测量仪器示意图图4 实验装置示意图 图4所示为实验装置,上方平台通过水平泡调节水平,弹簧上端与金属杆固连(图上连接点伸出平台较远,仅为展示),下端与传感器固连,传感器内置一个9轴陀螺仪芯片且带无线传输功能.实验时,在砝码盘中添加砝码,位移z可由刻度尺测得,角位移φ通过对传感器连续测得的角度取均值得到.弹簧参数如表1所示,联立表2中D的理论值,根据式(31)计算λ,其计算结果和百分差记录于表3、表4中. 表1 弹簧参数列表(材质:65 Mn钢) 表2 弹性系数解析解的理论值 表3 弹簧a实验数据 表4 弹簧b实验数据 对所得的λ在-z-λ图像上描点,与解析解式(31)(列于表2)比较,如图5所示. 图5 实验结果与理论结果对照图 z和φ的A类不确定度采用逐差法计算,B类不确定度Δz=1 mm,Δφ=10-4rad.D的合成相对不确定度取文献[10]用扭摆法给出的最大值0.28%. 弹簧a弹性系数λ的合成标准不确定度[11]为 ua=2.6×10-5kg·m·s-2(P=95%) (34) 其实验结果为 λa=(2.81±0.26)×10-4kg·m·s-2 (35) 弹簧b弹性系数λ的合成标准不确定度为 ub=2.2×10-5kg·m·s-2(P=95%) (36) 其实验结果为 λb=(1.84±0.22)×10-4kg·m·s-2 (37) 本文采用了文献中韦氏摆系统的拉格朗日函数唯象模型,建立了圆柱拉伸弹簧模型,从弹性力学角度出发给出了弹簧参数的应变和3个弹性系数的解析解.在条件式(24)下,本文通过文献结果验证了K、D的解析解,实验部分检验了弹性力学推导的正确性.该推导方法揭示了系统拉格朗日函数中唯象系数的物理意义,是分析实验现象,并完整地从理论角度解决一个物理问题的恰当实例.本文的弹性力学分析方法具有一定普遍性,同时简洁直观地对圆柱螺旋弹簧弹性系数的数学物理背景给出了明确的表述.

2.3 材料主应变的应变能
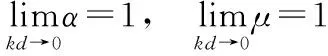
2.4 总弹性势能与分析





3 实验验证
3.1 实验原理

3.2 实验过程和结果





3.3 误差分析和实验结论

4 结论
