时间尺度上具有PS控制器的动态网络指数型同步

刘 捷，宾红华，黄振坤

(集美大学理学院，福建 厦门 361021)

0 引言

复杂网络[1]广泛存在于人类社会和自然界，现实生活中很多系统都可以被看作复杂网络，如通信、电网、互联网、控制工程及系统科学等。在模型上，复杂网络是由大量相互连接的单个节点组成，每个节点可以看作是一个具有一定动态特征和信息存储能力的动力系统，用边来表示节点之间相互作用。因此，复杂网络在这些动力学节点及其耦合连接的整体拓扑下，常常表现出非常复杂的运动特征。同步作为复杂动态网络中一种有趣而重要的集聚行为，所有节点利用它们之间的信息交换来驱动到共同状态，近年来得到了人们的广泛关注，并且有着广泛的潜在应用，如在机器人、飞行器和水下潜航器编队以及工业、电气、通信、生产等方面[2-3]。因此，一般动态网络的同步控制是一个值得深入研究的课题。

然而，由目前的文献可知，大部分关于连续时间[4]和离散时间[5]动态网络的同步工作是分开进行的。一方面，连续时间和离散时间复杂网络同步研究之间有许多重复的结果，因此在许多情况下，单独研究它们是多余的。另一方面，包含连续时间和离散时间的复杂网络同步更符合实际。例如，大脑中的一些神经元在白天是活跃的，在晚上是不活跃的，而它们在第二天会重新被激活，如此循环。此外，网络系统的时间域并不总是众所周知的连续时间间隔或离散时间域。因此，研究广义时间域上的复杂动态网络具有重要的意义[6]。为此，时间尺度理论(时标微积分)[7-8]提出了一种统一动态系统连续时间和离散时间的方法。如实数集R和整数集Z是2种特殊类型的时间尺度，基于时间尺度的复杂网络可以包含连续时间和离散时间，当选择实数集R作为时间尺度，可得到连续时间网络系统，选择整数集Z作为时间尺度，可得到离散时间网络系统。

目前，已有学者将时间尺度微积分理论引入复杂网络的同步研究，得到了很多很好的结果。如：文献[9]研究了在时间尺度上具有分布式牵制脉冲控制的动态网络的内外同步问题；文献[10]研究了复杂动态网络在时间尺度上的牵制同步；文献[11]研究了在时间尺度上的具有时变拓扑的复杂网络脉冲同步；文献[12]提出了在时间尺度上同时具有泄漏延迟和耦合延迟复杂动力系统的同步准则；文献[13]研究了非线性复杂网络的在时间尺度上的牵制间歇指数同步；文献[14]研究了在时间尺度上的基于事件的复杂网络的时间间隔牵制控制及应用；文献[15]导出了一类多智能体系统在时间尺度上的一致性准则；文献[16]引入时标型一致渐进稳定函数，并将改进的稳定性定理应用于多智能体系统，解决系统在时间尺度上的一致性问题。由此可以看出，在时间尺度上研究复杂网络的动力学可以简化和省去许多重复的工作。

众所周知，控制器在实现复杂网络同步过程中起着重要作用。复杂网络同步普遍的控制方法是在网络的每个节点上添加一个控制器。有代表性的控制方法包括激活反馈控制、线性分离控制、线性耦合控制、滑模控制等[17]。有效的控制策略有间歇控制、自适应控制、脉冲控制、采样控制、切换控制、事件触发控制等[18]。为了实现一般复杂动力系统在时间尺度上的同步，本文在文献[19]所提出的分布式PI控制的启发下，提出了PS控制器，解决了一般动态网络在时间尺度上的指数型同步问题,使复杂网络在包含连续时间和离散时间的广义时域上达到稳定状态。此外，本文在文献[20]模型的基础上，引用了文献[21]的定理，并在设计的PS控制器的作用下，实现复杂网络系统的指数同步，并将结果推广到更一般复杂时域的网络系统中。

1 预备知识和网络模型

本节给出了一些关于时间尺度的基本定义及相关概念。相关的理论背景可以参考文献[7-8]。

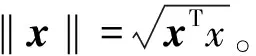
现考虑由N个相同的耦合节点构成的一般复杂动态网络，每个节点的状态方程[20]可以表述为

(1)

其中：x(t)=(xi1(t),…,xin(t))T∈Rn；f:Rn→Rn表示每个节点的内在动力学方程。A=(aij)∈RN×N是节点间耦合矩阵。如果节点i能收到来自节点j的信息，则aij=1;否则aij=0，i≠j，i,j=1,2,…,N，且aii=0。

设受控网络为:

(2)

其中ui为控制器。则误差方程为：

(3)

其中：ei(t)=(ei1(t),…,ein(t))T=yi(t)-xi(t)。

e△(t)=F(y(t))-F(x(t))+(A⊗In)e(t)+U,

(4)

其中：⊗表示Kronecker积；In是一个n×n的单位矩阵。

定义1 令f:T→R,t∈Tk，称f△(t)为f在t处的△-导数，若对任意ε>0，存在t的邻域U⊂T，有|[f(σ(t))-f(s)]-f△(t)[σ(t)-s]|≤ε|σ(t)-s|,∀s∈U,若f△(t)在任意的t∈Tk均存在，则称f是△-可微的。

引理1[7]若f,g:T→R在任意的t∈Tk上是可微的，则有f(σ(t))=f(t)+μ(t)f△(t)；(fg)△=f△g+fσg△=f△gσ+fg△。

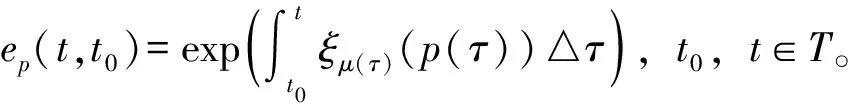
假设1 设F满足Lipschitz条件‖F(y(t))-F(x(t))‖≤υ‖e(t)‖,其中常数υ>0。

引理3[22]记x∈Rn,y∈Rn,则对任意l>0，有xTy+yTx≤lxTx+l-1yTy。

定义2 对系统任意的初始条件ψi(s)∈C([-τ,0]T,Rn)，存在常数ε>0、M>0以及一个足够大常数T>0，使得‖yi(t)-xi(t)‖≤Me⊖ε(t,0),t>T,i=1,2,…,N，则称网络(1)和控制网络(2)可实现指数型同步。

引理4[21]设V(t)是一个定义在时间尺度T上的函数且满足：

(5)

V(s)=|φ(s)|,s∈[t0-τ*,t0]T，

(6)

(7)

(8)

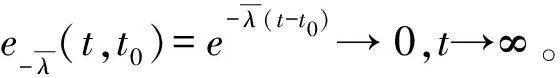
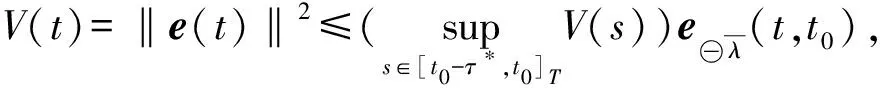
2 动态网络的指数型同步

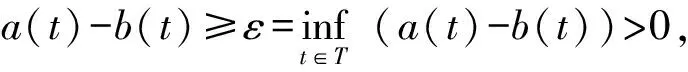
(9)

由式(9)可得

V△(t)+a(t)V(t)≤[2(υ+λmax(A⊗In)-σp)+μ(t)(υ+λmax(A⊗In)-σp)2+

a(t)+lσs+lμ(t)σs(υ+λmax(A⊗In)-σp)]eT(t)e(t)+

(10)

设计合适的σp和σs，使

2(υ+λmax(A⊗In)-σp)+μ(t)(υ+λmax(A⊗In)-σp)2+a(t)+lσs+

lμ(t)σs(υ+λmax(A⊗In)-σp)<0，

(11)

即

[2+μ(t)(υ+λmax(A⊗In)-σp+lσs)](υ+λmax(A⊗In)-σp)+a(t)+lσs<0，

(12)

从而

(13)

可令

(14)

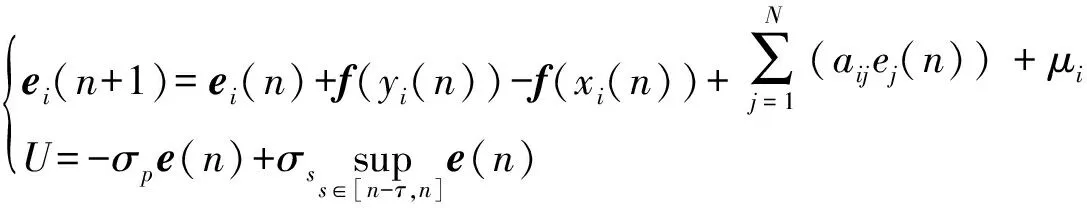
3 数值模拟

假设所有节点的初值在[-5,5]之间选取，基于定理1，可取σp=10，σs=1，l=1，a(t)<14.894 1，所以可取a(t)=10，b(t)=1.041 4。节点和误差的运动轨迹见图1～图3。

4 结论

本文研究了具有PS控制器的一般动态网络在时间尺度下的指数型同步问题。根据提出的PS控制协议，利用线性时滞动态方程及相应的不等式，得到了在时间尺度下动态网络指数型同步。推广了文献[20]和文献[21]的相关研究，使得动态网络同步的研究应用到更一般复杂时域的网络系统中。在今后的研究中，将继续推进在时间尺度下动态网络同步的研究，具体研究动态网络在时间尺度下不同控制策略的同步问题，如时间尺度下的牵制控制、脉冲控制以及切换控制等。