稠度和弯角在高亚音扩压叶栅中的耦合作用
2022-02-18陶船斯嘉王松涛王春雪王仲奇
陶船斯嘉,杜 鑫,王松涛,王春雪,王仲奇
(1.哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001;2.北京动力机械研究所,北京 100074)
在高亚音叶栅中通过增加折转角、降低稠度和展弦比来提高叶片负荷。随着叶片负荷的不断提升,叶栅流道内的横向压力梯度同时增大,导致吸力面角区分离流动更为复杂。因此,需要应用流动控制手段来控制端区分离流动,提升角区通流能力,降低二次流损失,提高叶栅性能。
之前的研究已经表明:弯叶片可通过改善流场结构,提高压气机的气动性能。张华良[1]通过研究发现合适的正弯和前掠可以升高吸力面上由端部指向叶展中部的“C”型径向压力梯度,减小端壁附近的逆压梯度,促进角区分离形态由闭式分离向开式分离转化,缩小角区分离的覆盖范围,降低端区损失。凌敬[2]在弯叶片叶栅中建立叶栅损失模型和落后角模型,探究NACA65叶型叶栅中最优弯角随模型参数的变化规律。阚晓旭[3]等人应用拓扑分析探究弯叶片叶栅中流动结构的演变规律,并将损失分成不同分类,探讨不同类型损失权重。虽然前人已在亚声速扩压叶栅中应用弯叶片做了大量的研究工作,但针对高亚声速来流环境下弯叶片的作用机理还缺乏系统性认识。
NASA早期的研究指出,在压气机初始设计中,稠度是一个重要参数,它的选取影响着气流折转能力、叶片负荷能力和工作范围[4-6]。合理选取稠度在初始设计和通流设计中至关重要[7-8]。
本文的研究对象为某三级压气机的中间级静叶栅,研究高亚音扩压叶栅中稠度和弯叶片的作用规律,探索弯叶片的普适性条件。分析了不同稠度和弯角下的变冲角特性,包括总压损失、扩压因子等。研究最小损失冲角工况下弯角对扩压能力、流动损失的影响。然后通过讨论总压损失系数的展向分布、叶片吸力面和端壁上的极限流线及压力梯度云图,分析了弯叶片对扩压叶栅损失影响的原因,以及大稠度时弯叶片对流场结构和损失机理的影响。
1 研究方案与数值方法
1.1 研究方案
用于本文研究对象的平面叶栅原型来自于某三级高负荷低反力度压气机的中间级静叶,应用本课题组前期开发的自有造型程序进行叶型生成工作,叶型具体参数见参考文献[9]。原型的折转角为44°,为创造高负荷扩压环境,本文选取折转角为50°。为了控制端区流动分离,减少低能流体在角区的堆积,需选用较高的子午收缩程度,本文采用的子午收缩比为0.8。原型中径处稠度为1.86,根据稠度常规取值和选取范围全面的需要,本文稠度取值为1.4-2.2。参考之前的研究结果,弯高采取50%叶高,弯曲形式为正弯,弯角取值范围5°~30°。本文的研究方案和来流条件如表1。采用枚举法对上述方案中所有的稠度与弯角取值组合进行数值计算,并在每个叶栅方案中均开展变工况数值模拟,在叶栅稳定工作范围内寻得最小损失冲角。
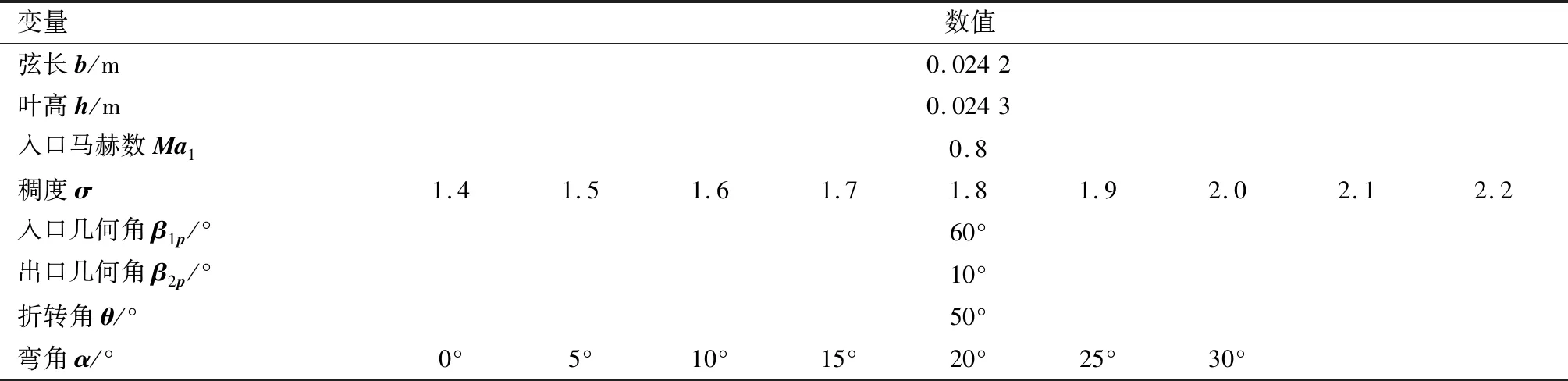
表1 叶栅参数
1.2 数值方法与验证
本文的网格划分工作采用商业化软件NUMECA软件包的IGG/Auto Grid5模块,网格拓扑采用H-O-H 型结构化网格,网格总数197万,网格示意图如图1。数值计算采用商业软件ANSYS软件包中的CFX流体动力学数值分析程序。计算模型上,根据叶栅适用条件和计算需求选用SST湍流模型耦合γ-θ转捩模型,同时应用高精度差分格式在对流项。为满足湍流模型的求解要求,壁面附近第一层网格的宽度设定为10-3mm,得到计算结果壁面上的Y+值不超过4。边界条件中,叶栅入口的总温为440 K,总压为430 kPa,并同时给定入口气流方向;叶栅出口通过根据入口气流方向调整质量流量,以保证入口马赫数0.8不变,同时来流湍流度为5%。采用Bo Song论文中[10]来流条件和叶型折转角与本文研究对象相似的高负荷MOGA叶型进行数值方法的验证,将数值计算结果与实验数据进行对比验证。叶型和叶栅的几何定义见图2,参数取值见表2。
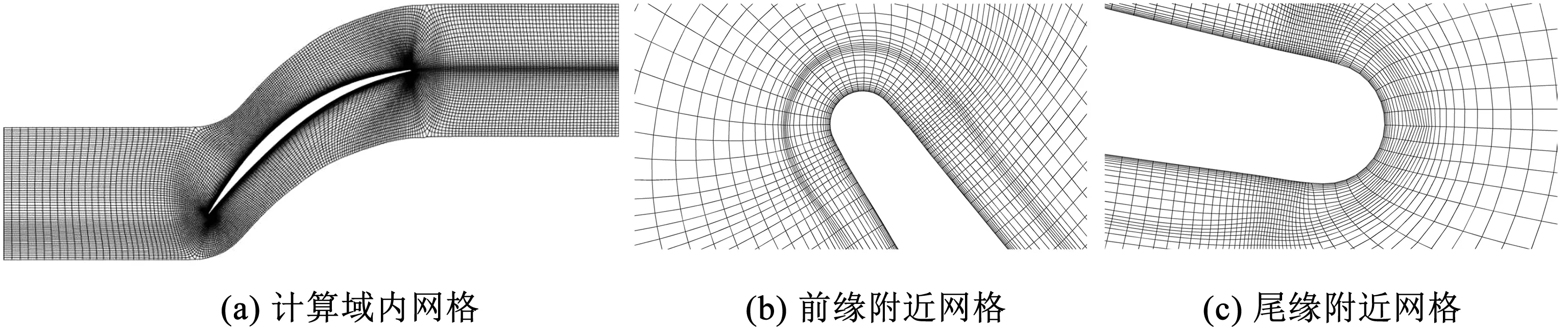
图1 计算使用网格示意图
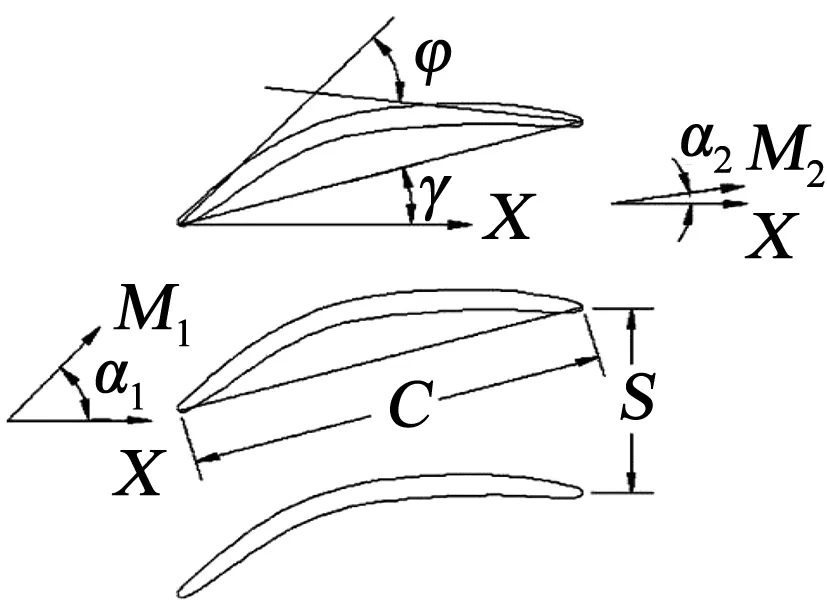
图2 叶型和叶栅的几何定义
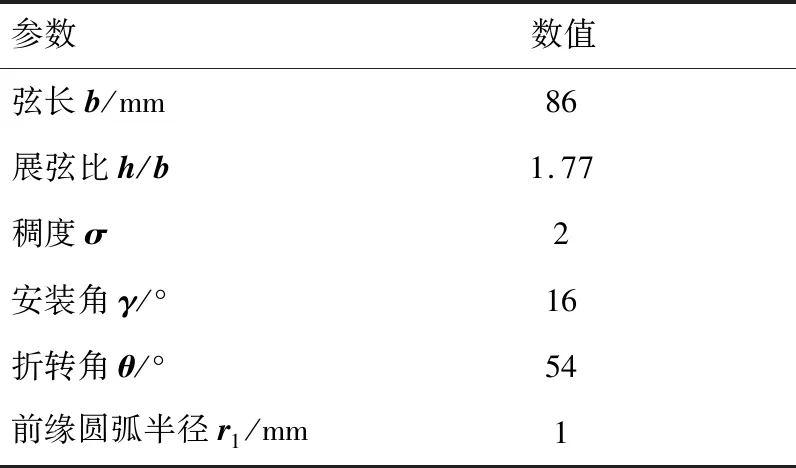
表2 MOGA叶型叶栅参数
图3所示为来流马赫数为0.77时,叶型表面等熵马赫数的轴向分布的数值与实验结果对比。选择此工况的原因是本文的来流马赫数为0.8,与此工况相近。由图可知,数值计算数据与实验结果在整体趋势上吻合,本文所用数值方法可以基本上实现对高亚音大折转角叶型流场的模拟。
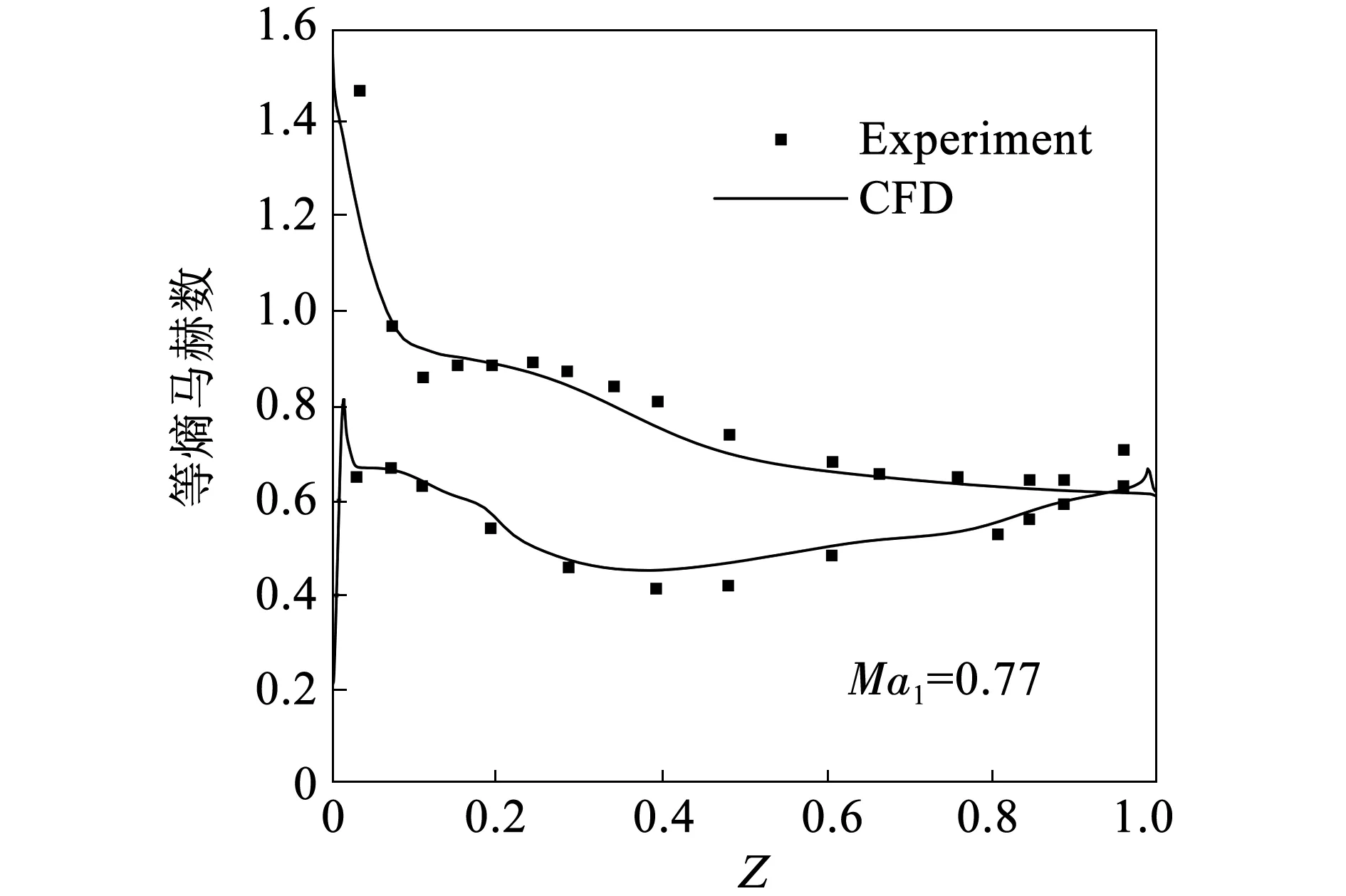
图3 Ma1=0.77时轴向等熵马赫数分布
2 气动性能
2.1 变冲角特性
图4所示为直叶栅和弯曲叶栅(α=10°,20°和30°)中的冲角特性。从图中看出,无论是直叶片还是弯叶片,随着稠度的增加,总压损失变冲角特性曲线都移向正冲角方向,最小损失冲角也往正冲角方向迁移,且低损失工作范围逐渐缩小。在最小损失冲角工况下,总压损失系数随着稠度的增大而增大。直叶片时,最小损失冲角点同时也是近失速点,冲角大于最小损失冲角时损失急剧增加;当叶栅为正弯10°,稠度不超过1.8时也存在这样的现象。在最小损失冲角下,对于直叶片和弯叶片,改变稠度对叶栅扩压能力的影响均有限。在弯叶片叶栅中,随着弯角的增加,在叶栅稳定工作范围内,总压损失系数显著降低,且稳定工作范围有向正冲角方向逐渐扩宽的趋势。这说明随着稠度的升高,正弯叶片可以更显著地改善流动损失,有效提高叶栅的气动性能。其可能原因在于叶片弯曲可以改善流场,削弱二次流动,气流折转大,叶栅扩压能力增强。总的来说,无论是叶栅扩压能力还是稳定工作范围,弯叶片相较于直叶片均有所提升。

图4 变冲角特性线
2.2 总体性能
最小损失冲角工况下的总压损失系数和扩压因子随弯角的变化情况如图5所示。由图可以看出对于固定稠度的叶栅,弯角增加使最小损失冲角略微增加,降低损失的同时提高扩压因子。在大稠度(σ≥2.0)条件下,弯角增加对损失降低的效果更明显;小稠度下弯叶片虽然降低损失不很明显,但会显著提升叶栅扩压因子。另外,当稠度从1.4增加到2.2的过程中,最佳弯角(即使损失最低的弯角)从20°增加到30°,说明稠度增加使最佳弯角增加,这一结论也可以从之前的冲角特性分析中看出。
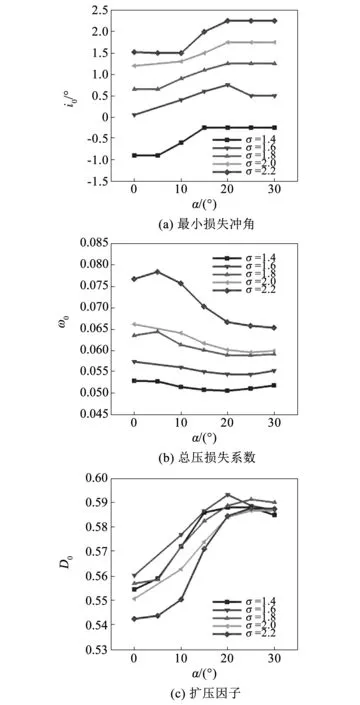
图5 弯角对最小损失冲角下叶栅气动性能的影响
3 分析与讨论
3.1 总压损失的展向分布
图6所示为两个不同稠度下,直叶栅(α=0°)和正弯(α=20°,30°)叶栅的损失沿叶高分布。图(a)显示,小稠度时,弯角20°和30°均能降低端区损失,且增加叶展中部损失,两项抵消,因此对总压损失的改善不明显。大稠度时,弯角20°和30°均能同时降低端区损失和叶展中部损失,此时弯叶片使总压损失显著降低。对比两个不同的弯角20°和30°可以发现,无论是对于小稠度还是大稠度,30°弯角都比20°弯角的中部损失高,端区损失低。但在低稠度(如图5(a))时,与20°相比,30°弯角会更多增加叶展中部损失,比它降低的端区损失更多,因此小稠度时弯角20°的总损失比30°更低,最佳弯角在20°。大稠度(如图5(b))时,相比于20°弯角,30°弯曲叶栅虽然在叶展中部损失更高,但对端区损失降低得更多,因此大稠度时最佳弯角为30°。

图6 弯角对总压损失系数沿展向分布的影响
3.2 壁面极限流线与压力梯度
图7为直叶栅和弯曲叶栅在三种不同稠度下的吸力面极限流线与径向压力梯度,以及端壁面上的极限流线和横向压力梯度。可以看出在各种不同稠度下,叶片弯曲均削弱了角区分离流动。由壁面压力梯度可以看出,叶片弯曲增强了端区的径向压力梯度,使角区低能流体向叶展中部迁移,削弱角区分离流动。但叶片弯曲使端壁上的横向压力梯度增强,端壁附面层迁移能力增强,通道涡增强。在增强的径向压力梯度和流向逆压梯度的共同作用下,端壁附面层和通道涡沿着吸力面向上迁移,造成了叶展中部回流增强,回流范围扩大。

图7 壁面极限流线和吸力面以及端壁压力梯度
4 结论
采用数值模拟方法计算了直叶栅和弯曲叶栅在9个稠度下的变冲角特性,分析稠度和弯角对叶栅在最小损失工况下的气动参数的影响,得到以下结论:
(1)在直叶栅和弯曲叶栅中,稠度增加使最小损失冲角线性增加,最小损失增大,且直叶栅中稠度增加带来的损失增加要比弯曲叶栅中更显著。
(2)弯角增加时,最小损失冲角略微增大,最小损失整体呈降低趋势,此冲角下的扩压因子增大。弯角的加入会在各个稠度下改善叶栅气动性能,尤其是大稠度高损失叶栅中,弯曲叶片作用更显著。
(3)随着稠度的增加,需要叠加更大的弯角来实现最低损失:小稠度(σ=1.4)时,损失最低弯角为20°;大稠度(σ=2.2)时,损失最低弯角为30°。弯角的选择需要与稠度取值相匹配。
