土压平衡盾构改良渣土屈服应力分析
2022-02-18熊欢刘绍兴孙利辉屈春来1冷先伦刘世伟1
熊欢, 刘绍兴, 孙利辉, 屈春来1,, 冷先伦, 刘世伟1,,*
(1.河北省智慧水利重点实验室, 邯郸 056006; 2.成都兴城建设管理有限公司, 成都 610000; 3.河北工程大学水利水电学院, 邯郸 056006; 4.中科院武汉岩土力学研究所岩土力学与工程国家重点实验室, 武汉 430071)
土舱内渣土改良是土压平衡盾构隧道工法的重要技术环节,渣土的改良效果直接影响着开挖面的稳定性和机舱内渣土的运输状态[1]。和易性是改良渣土的重要特性之一,反映了渣土自身的流动特征,改良渣土和易性差极易诱发刀盘扭矩大且磨损严重、千斤顶推力大、土体饼化堵舱、喷涌等问题,进而导致掌子面支护压力不足、甚至塌方等一系列事故[2-3]。因此,有必要针对改良渣土的和易特性及其评价指标进行深入研究。
中外学者已针对该问题开展了诸多研究并取得了丰富成果。Zhen等[4]通过室内塌落度试验,获得不同含水率条件下砂土和卵石与改良剂的最佳混合比;Peila等[5]综述评价了改良土体性能的评价方法,结果表明塌落度试验是目前土压盾构隧道中常用的改良土体和易性评价方法;Wei等[6]和 Huang等[7]基于室内塌落度试验,评价了不同泡沫改良剂掺入比和不同泥浆掺入比条件下,砂卵石改良土的和异性变化特征;Kim等[8]对不同含水率和不同泡沫剂掺入比组合工况下的风华花岗岩残积土改良后的和易性进行了室内塌落度试验分析;蔡兵华等[9]采用室内塌落度试验方法对改良后的红黏土流动特性进行了分析;此外,张研等[10]、贺少辉等[11]和闫潇等[12]采用塌落度实验方法对砂土地层和卵石地层盾构隧道改良渣土的和易性进行了研究。可见,目前对土压平衡盾构隧道改良渣土的和易性评价基本采用室内塌落度试验方法。
事实上,塌落度值并不能反映与材料自身相关的物理力学性质,而屈服应力是反映材料和易性的重要流变特征参数之一,它是指材料开始或停止流动的临界应力[13]。材料的屈服应力通常采用室内流变仪试验获得,而这种方法不适用于工程现场存在粗粒土情况,且测试费用昂贵[14]。塌落度试验对土体粒径的适用范围较广,如何确定塌落度值与改良渣土屈服应力之间联系,进而在塌落度实验基础上对材料和易性进行定量评价分析,具有重要的工程应用价值[15]。而各国的塌落度试验标准并不一致,主要有美国材料协会(American Society for Testing and Materials,ASTM)标准塌落度试验、圆柱塌落度试验和AS2701.5圆锥塌落度试验等[16],致使关于塌落度试验与屈服应力预测模型尚未形成统一意见,应用到土压盾构渣土屈服应力分析方面的研究成果相对更少。
有鉴于此,现以武汉地铁6号线老关村出入段盾构隧道工程为背景,进行角砾黏土改良体室内塌落度试验分析;考虑塌落度桶形状效应,提出渣土屈服应力改进预测模型,并与既有成果对比分析,验证本文改进模型的有效性;进而对不同含水率、不同角砾含量和不同泡沫剂掺入比条件下的角砾黏土屈服应力变化规律开展分析。以期为土压盾构渣土改良施工提供支持,保障土压平衡盾构隧道的安全作业。
1 室内塌落度试验
选取武汉地铁6号线老关村出入段盾构隧道区间为依托工程,根据现场勘察结果显示,土压盾构主要穿越角砾黏土地层,现场取样并进行室内筛分实验,土体颗粒形态如图1所示。并获得试验土样的颗粒级配,其中角砾含量超过60%,如表1所示。
根据现场实际情况,室内改良试验选取工程所用泡沫剂对土样进行改良并进行塌落度试验,本次塌落度试验中采用ASTM标准塌落度桶,搅拌发泡后的改良剂与塌落度试验装置如图2所示。工程中常用泡沫剂浓度为2%~7%,本次试验中选取泡沫剂浓度为4%,重点分析土体含水率、泡沫剂掺入比(体积比)以及角砾含量(质量比)3个因素对土样塌落度的影响。具体试验方案如下。

d为土颗粒粒径大小图1 试验土样颗粒级配情况Fig.1 Particle size distribution of test soil sample
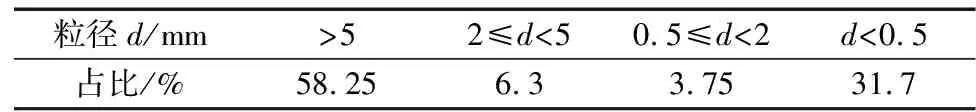
表1 角砾黏土层粒径分布Table 1 Particle size distribution of breccia clay layer

图2 发泡后改良剂与塌落度试验装置Fig.2 Improver after foaming and slump test device
(1)泡沫掺入比为0条件下,不同含水率(25%、30%、35%和40%)、不同角砾含量(30%、50%和70%)时,测量土样塌落度值。
(2)含水率为25%条件下,不同掺入比(20%、30%、40%和50%)、不同角砾含量(30%、50%和70%)时,测量土样塌落度值。
角砾含量为70%,泡沫掺入比为40%和50%时的土体试样塌落形态如图3所示。不同含水率、不同掺入比、不同角砾含量角砾黏土试样塌落度试验测试结果,如表2所示。由表2可知,含水率越高,角砾黏土试样塌落度值越大;角砾含量越大,试样塌落度值越大;掺入比越高,试样塌落度值越大;含水率、角砾含量和泡沫掺入比与角砾黏土塌落度值呈正相关关系。

图3 土样塌落形态Fig.3 Collapse shape of soil sample
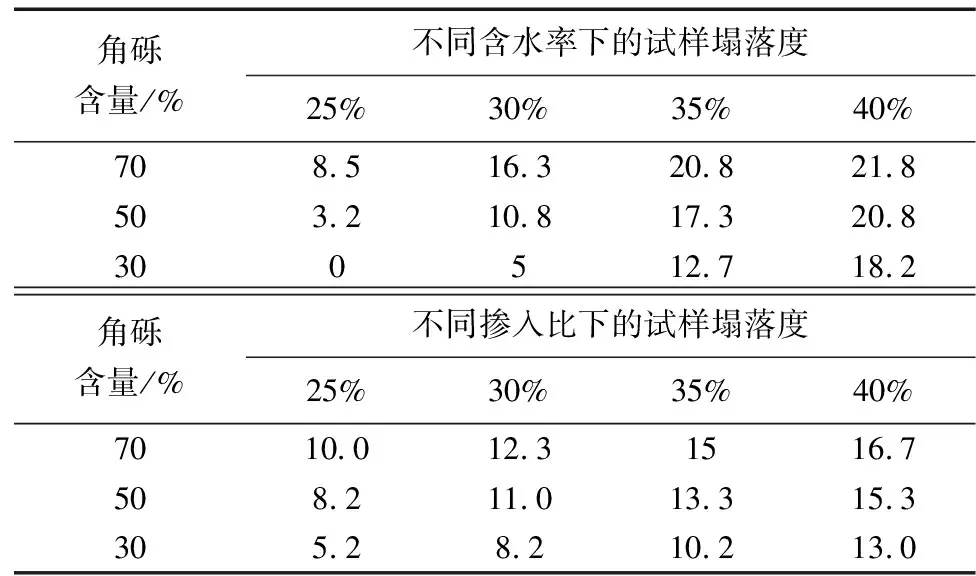
表2 不同角砾含量、不同含水率和不同掺入比 下试样塌落度试验结果Table 2 Experimental results of slump test under different content of breccia, different moisture content and different mixing ratio
2 渣土屈服应力改进预测模型
2.1 改良渣土屈服应力模型推导
塌落度筒内土体变形前后的形态如图4所示。变形前距离原点O处的z平面,在变形后成为z′处平面。为了便于推导,假设以下两个条件:①土体材料为均匀、连续且各向同性;②土体材料不可压缩。
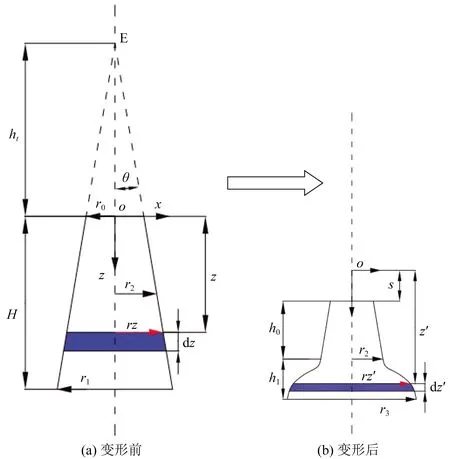
O、x、z分别为坐标系的原点、x轴和z轴;H为塌落度筒高度;r0为塌落度筒筒顶圆半径;r1为塌落度筒筒底圆半径;rz为距离原点为z处的截面半径;E为塌落度筒两条母线的交点;ht为E点与塌落度筒筒顶的距离;θ为塌落度筒母线与轴线的夹角;dz为塌落度筒内材料变形前的微分单元厚度;dz′为厚度为dz的微分单元坍塌变形后的厚度;r′z为厚度为dz的微分单元坍塌变形后的半径;r3为材料坍塌变形稳定后的底面半径;r2为发生坍塌变形段与未发生坍塌变形段交界面的半径;h0为未发生坍塌变形段的高度;h1为坍塌变 形段变形稳定后的高度;s为塌落度图4 塌落度筒内土体变形前后的形态Fig.4 Shape of the soil body before and after deformation in the slump test device
结合图4(a)中的几何关系可得
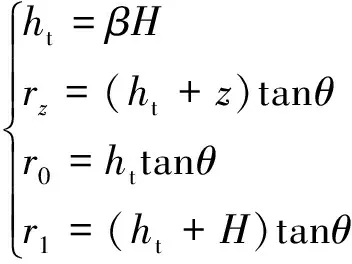
(1)
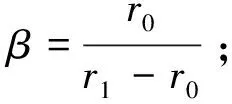
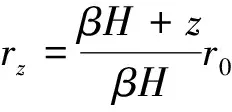
(2)
任意水平截面z上方的材料重力wz为
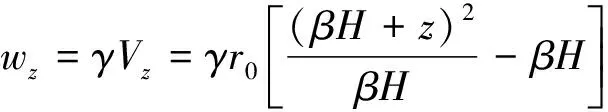
(3)
式(3)中:γ为材料的重度;Vz为水平截面z以上材料的体积。
任意位置z处水平截面上的压应力为
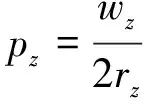
(4)
将式(2)和式(3)代入式(4)中,水平截面z处的压应力为
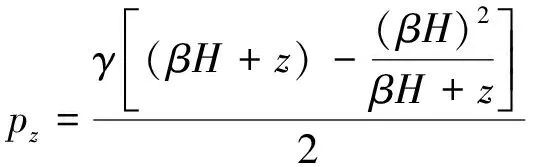
(5)
根据Tresca准则,水平截面上的最大剪切应力为所施加压应力的一半,也即为材料的屈服应力[14],则任意水平截面z处的最大剪切应力为
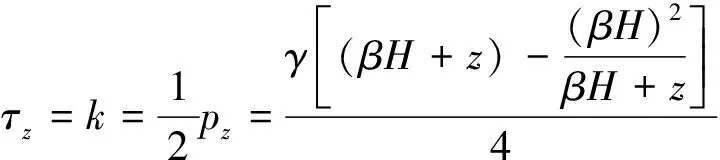
(6)
式(6)中:k为材料的屈服应力。
选取塌落变形段内微单元dz为对象,屈服变形后为dz′,进行变形前后受力平衡分析和对比分析,可得
(7)
结合图4可知,变形稳定后屈服区的高度h1可表示为
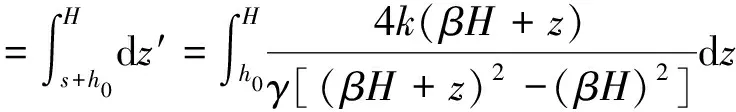
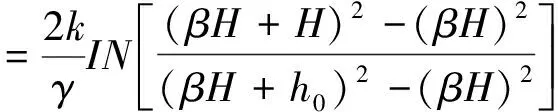
(8)
结合图4,自塌落度筒顶部沿z轴方向存在一距离h0,塌落屈服变形段内的屈服应力为k,z=h0截面处土体处于临界屈服状态,由式(6)可得
(9)
采用塌落度筒高H和土体材料重度γ归一化处理,得无量纲屈服应力k′表达式为
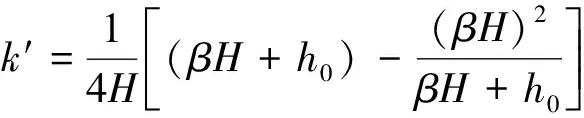
(10)
求解式(10)可得h0的表达式为
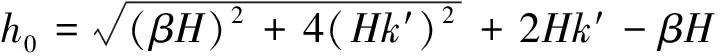
(11)
根据图4(b)可知,塌落度s为
s=H-h0-h1
(12)
经过塌落度筒高H归一化处理,塌落度的无量纲形式s′表示为
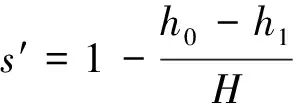
(13)
结合式(8)、式(11)和式(13)可求解得出无量纲屈服应力k′和无量纲塌落度s′之间的关系模型。
可根据β不同取值,对不同形状塌落度试验进行材料屈服应力评价。
2.2 模型验证
为了能够更好地验证本文计算模型的可靠性,总结了3种典型圆锥形塌落度筒尺寸进行对比分析,其对应的尺寸情况如表3所示。结合表2,当β→∞时,式(13)可用于圆柱形塌落度试验进行材料屈服应力预测;当β=1、H=300 mm时,式(13)可用于ASTM试验进行材料屈服应力预测;当β=1、H=150 mm时,式(13)可用于AS2701.5试验进行材料屈服应力预测;当β=0.8、H=75 mm时,式(13)可用于Saaka等[14]圆锥塌落度筒进行材料塌落度试验和屈服应力评价。
针对上述3种典型圆锥形塌落度桶尺寸,本文模型计算结果与试验结果进行对比分析,如图5所示。针对圆柱形塌落度桶尺寸,本文模型计算结果与试验结果进行对比分析,如图6所示。由图6中分析可知,本文模型预测结果与试验结果吻合度较好,表明本文模型可用于材料屈服应力的预测分析。
由本文提出的计算模型与其他理论模型计算结果的对比分析,如图7所示。由图7可知,①本文模型计算结果均位于现有理论模型计算结果之间,表明本文模型的可靠性;②提出的ASTM模型计算结果大于Saaka等[14]的圆锥模型计算结果,结合图4可知,本文ASTM模型计算结果更加符合实验结果的变化规律,这主要是由于本文模型中考虑了塌落度试验桶形状效应影响。
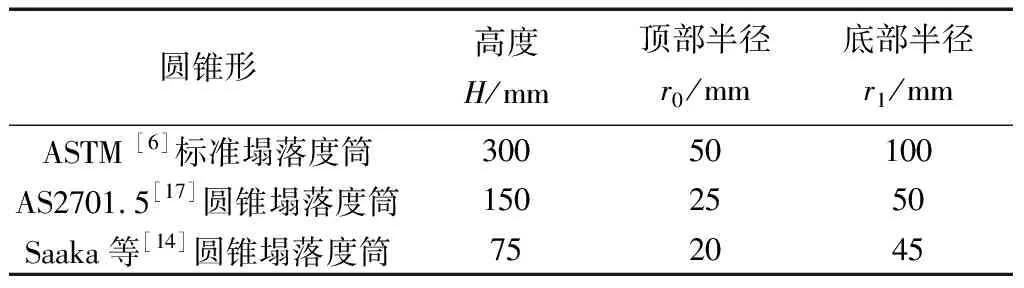
表3 3种典型塌落度筒尺寸Table 3 Three typical slump test device
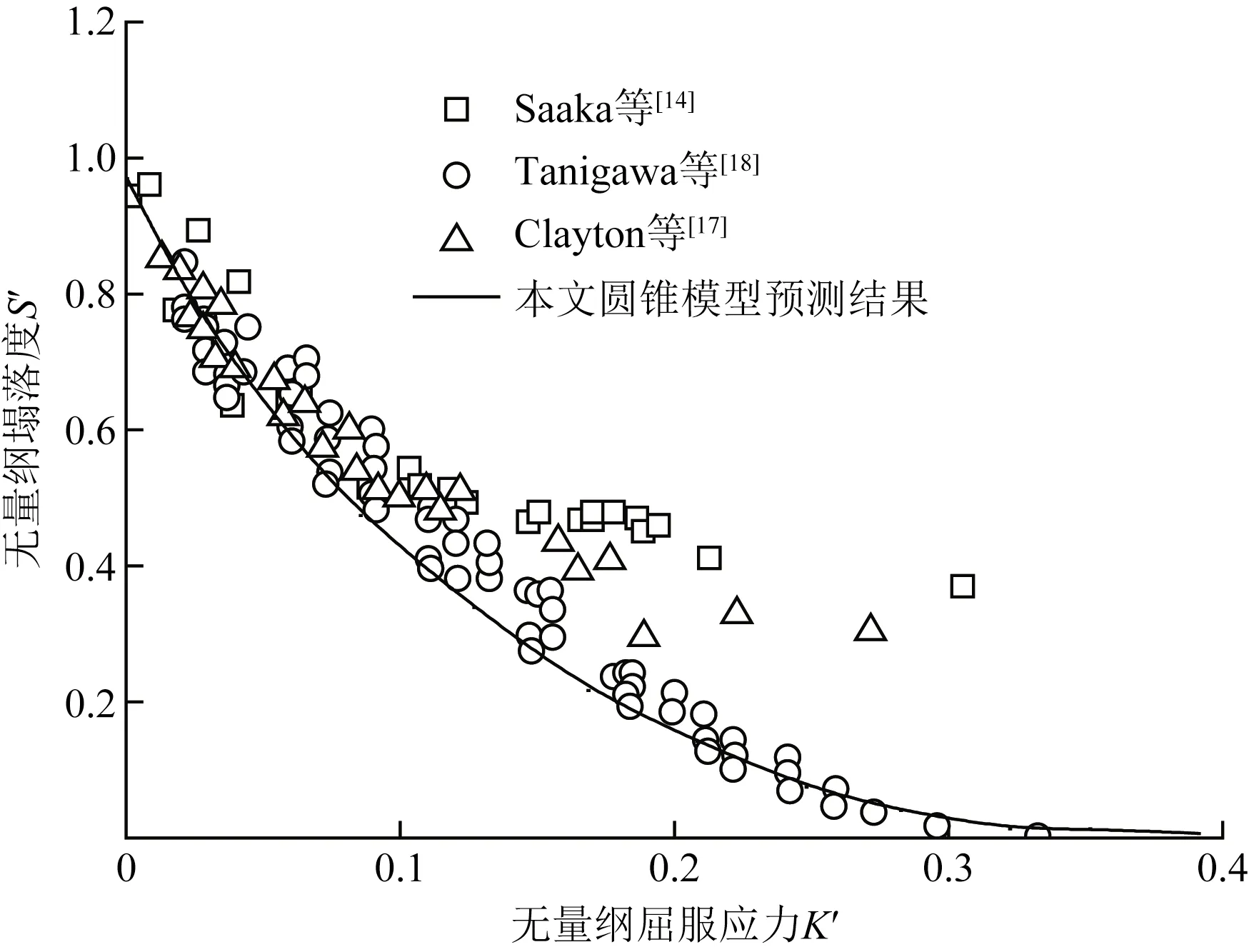
图5 圆锥形塌落度模型的计算与实验结果对比分析Fig.5 Calculation of conical slumping model is compared with the experimental results
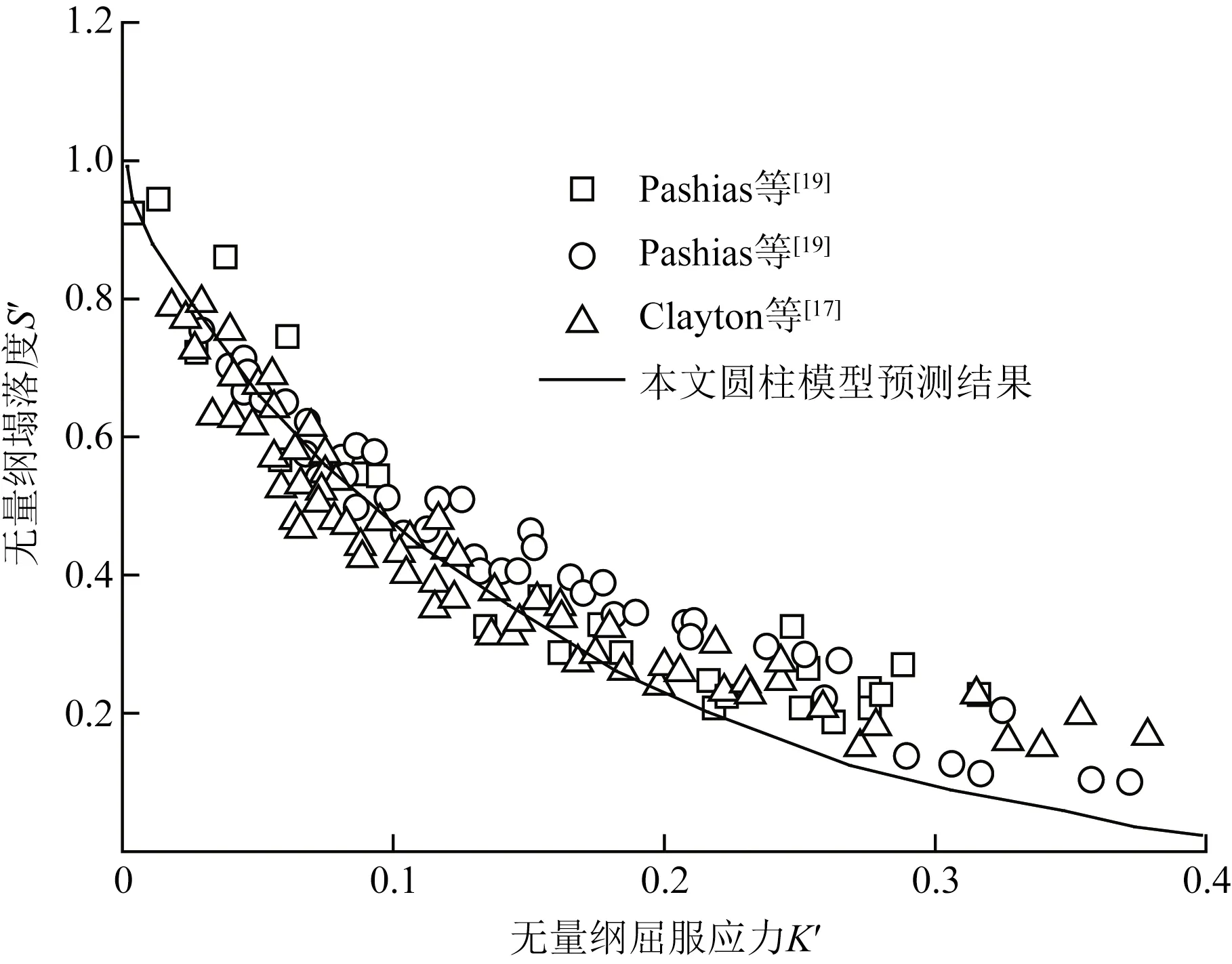
图6 圆柱形塌落度模型的计算与实验结果对比分析Fig.6 Calculation and experimental results of cylindrical slumping model are compared and analyzed
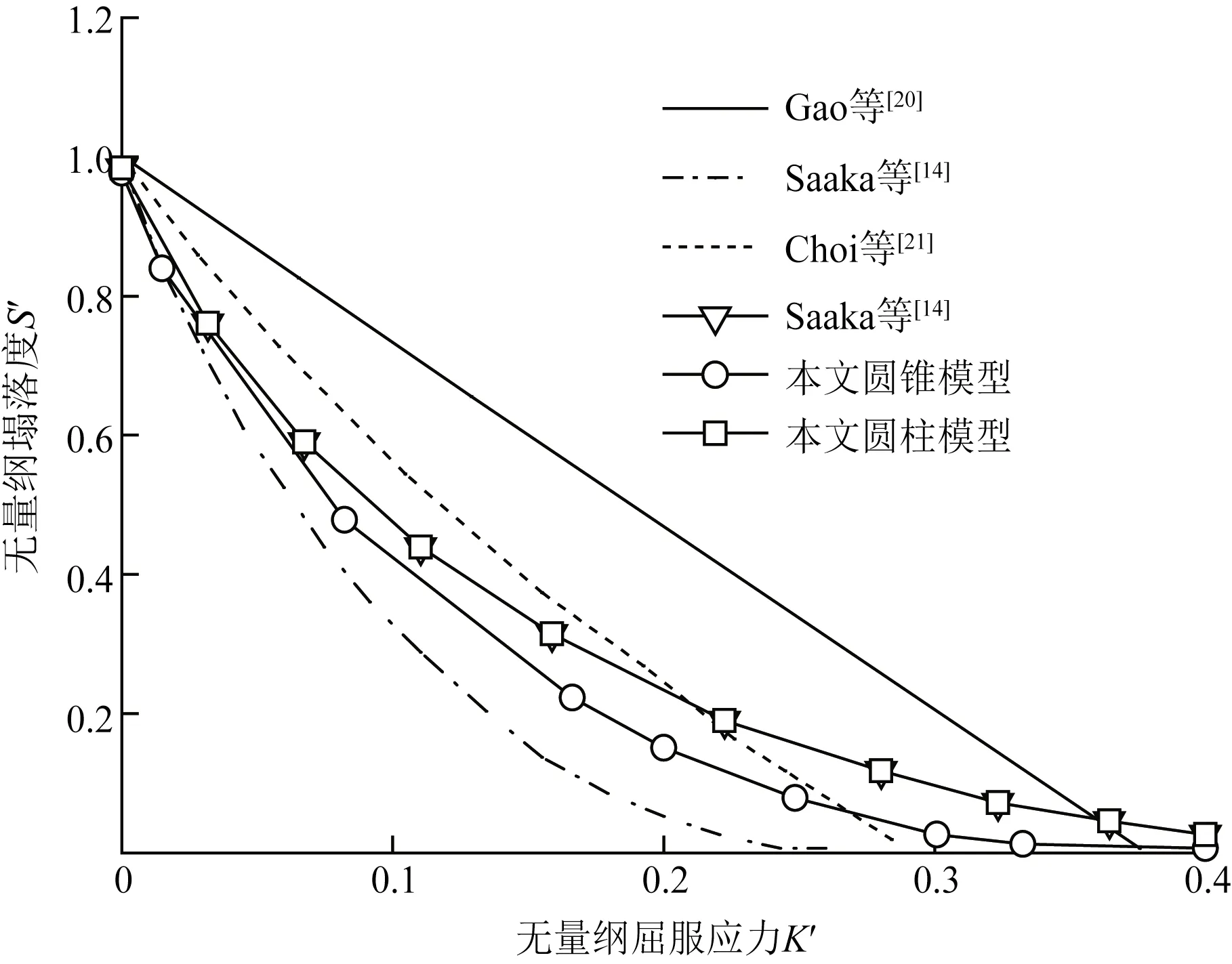
图7 本文模型与其他理论模型计算结果对比分析Fig.7 Calculation results of this model are compared with those of other theoretical models
3 改良渣土屈服应力变化规律分析
结合室内改良渣土塌落度试验结果,采用本文模型可获得不同含水率、不同角砾含量以及不同泡沫剂掺入比条件下,改良渣土的屈服应力变化规律,如图8所示。由图8分析可知,含水率越大,角砾黏土的屈服应力越小,二者呈现明显非线性负相关;含水率越低,角砾含量对土体屈服影响越明显,当含水率增大到一定程度时,角砾含量对土体屈服应力的影响可忽略。泡沫剂掺入比越高,角砾黏土的屈服应力越小,二者基本呈现线性负相关;不同泡沫掺入比条件下,角砾含量对土体试样屈服应力的影响几乎一致。总的来说,不同含水率和不同泡沫剂掺入比条件下,角砾含量越高,则土样屈服应力越小,这主要受到角砾土的颗粒体松散特性影响而至。
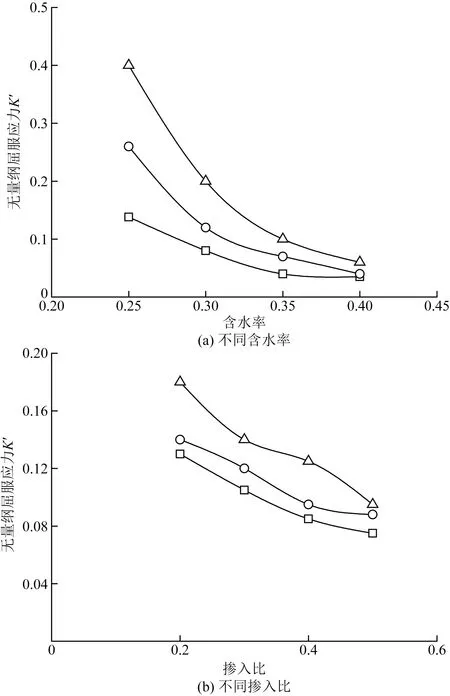
图8 角砾黏土屈服应力变化规律Fig.8 Variation law of yield stress of breccia clay
4 结论
(1)通过不同含水率、不同泡沫剂掺入比和不同角砾含量条件下室内塌落度试验分析表明,含水率、角砾含量和泡沫剂掺入比与角砾黏土塌落度值呈正相关关系。
(2)提出一种考虑塌落度试验筒形状影响的的改良渣土屈服应力改进预测模型,并与实验结果和其他理论结果对比分析,验证了本文模型的可靠性。
(3)角砾含量越高,土体屈服应力越小;角砾黏土屈服应力与泡沫剂掺入量呈现线性负相关,而与含水率的非线性负相关关系特征明显。
