描述砂性土宏细观力学关系的数学模型

闫洪超， 鲁杰， 饶振兴， 翟洪涛， 关鹏

(1. 河南省地质矿产勘查开发局第四地质勘查院， 郑州 450000； 2. 中国地质大学工程学院， 武汉 430074)

由地质作用或人工碎裂形成的土既可作为建筑材料，如砖、瓦、混凝土骨料等，又可作为地基或路基承受荷载[1-2]。其力学特性是土力学最关注的问题之一。土体总是被当成连续介质，这是因为，当土被视为连续介质时，可采用连续力学理论来研究土体，进而构建基于连续介质理论的应力-应变本构关系，用于服务工程建设。实践证明，采用连续介质力学理论研究土体是可行的，解决了很多实际工程问题。然而土体毕竟是由土粒构成的，把它视为连续介质理论上是行不通的，土体力学行为的研究最终应回归土粒或土粒群[3]。自颗粒流离散元方法问世以来，砂性土细观颗粒层面的力学行为得到了深入的研究，为构建土体宏观力学响应与土粒相关的细观力学行为之间的联系提供了途径，突破性的研究成果不断出现，Christoffersen等[4]基于准静态平衡理论，提出了采用粒间接触力表述砂性土等颗粒材料宏观应力张量的方法。Oda[5]提出采用二阶组构张量描述颗粒材料颗粒定向、接触力大小和方向的各向异性。砂性土在荷载作用下宏观应力张量发生变化时，必然会有粒间接触力各向异性的变化。Rothenburg等[6]提出采用傅里叶级数描述粒间接触力的各向异性，并建立起了细观接触力各向异性指标与宏观应力比的关系，同样的，砂性土在荷载作用下宏观应变张量发生变化时，必然会对应着与体积相关的某一细观指标各向异性的变化。Kruyt等[7]将相互接触的颗粒形心连接成多边形，且定义了多边形的方向，试样在变形过程中多边形的方向表现出各向异性，基于此，建立了宏观应变与多边形方向各向异性指标间的关系。

虽然宏观应力和应变已经与细观接触力和孔隙多边形各向异性建立起了联系，但这些结论均基于对某种试验数据的唯象总结，缺乏理论依据。Rothenburg等[6]提出的宏观应力比与接触力各向异性指标的联系仅适用于三轴压缩试验，而对于直剪试验则不适用。针对这个问题，基于已有研究，现采用理论推导和数值试验验证相结合的方法建立通用的粒状砂性土宏观应力与细观接触力各向异性指标的关系。以期为构建砂土宏细观本构模型提供新途径。

1 颗粒流离散元方法

颗粒流离散元法以粒间接触为计算单元，基于力-位移法则和牛顿第二运动定律，采用显式积分算法模拟颗粒在粒间接触力作用下的运动。采用Itasca[8]公司的颗粒流离散元软件PFC3D进行计算，计算流程如图1所示。

图1 PFC计算流程简图Fig.1 PFC calculation flow diagram

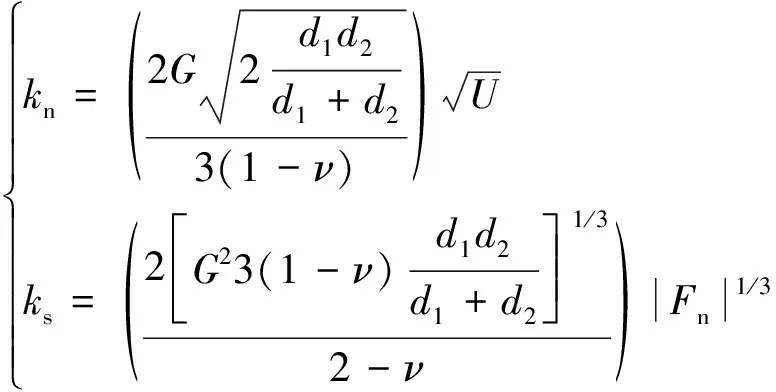
(1)

式(1)中：d1和d2为相互接触的两个颗粒的半径，m；G和ν为接触的剪切模量和泊松比，参考Mitchell等[3]总结的硅质砂的力学指标范围，取90 GPa和0.2；U为接触的重叠量，m；Fn为法向接触力，N。由式(1)可知，接触的刚度kn和ks是与接触重叠量相关的，重叠量越大，刚度越大。另外，接触法向力与

I和J为两个相互接触颗粒的代号；l(IJ)为相互接触的颗粒形心距；δ(IJ)为两颗粒在接触处的重叠量；及为X轴和Y轴方向上 的单位向量图2 Hertz接触模型简图Fig.2 Schematic diagram of Hertz contact model

接触切向力满足Mohr-Coulomb准则：

Fs≤μFn

(2)

式(2)中：μ为颗粒的摩擦系数。

2 数值模型的建立

采用颗粒流离散元软件PFC3D进行数值建模，在边长为1 m的立方体计算空间中生成5 000个粒径为0.01 m的球形颗粒，颗粒摩擦系数设为零，由于颗粒粒径很小，悬浮在空间中，互不接触。计算空间的边界为周期性边界，当颗粒形心越过边界后，颗粒不会消失，会以相同的速度出现在空间中中心对称的位置处，这种设置消除了刚性边界条件的影响，用于模拟土粒真实的受力环境。采用自定义的功能函数，持续放大颗粒的粒径，直到空间中颗粒的体积分数超过52.36%时停止。等粒径的颗粒在三维空间中能堆积出的最松散结构为正六面体结构(六面体的每个节点位置上有一个颗粒)，对应的最大的孔隙率是47.64%，而在三维空间中能堆积出的最密实结构为正四面体结构(四面体的每个节点位置上有一个颗粒)，对应的最小的孔隙率是25.95%。所以当颗粒的体积分数达到52.36%时，理论上对应空间中最松散状态时的孔隙率，此时改变颗粒的摩擦系数为0.5，模型如图3所示。在最松散的孔隙率下，由于颗粒未能形成正六面体结构，因此，颗粒系统处于流动状态(unjammed state)。继续放大颗粒粒径或减小计算空间，会增加平均颗粒配位数，使颗粒系统由流动状态变为阻塞状态(jammed state)。自然界中，土体在未破坏之前常处于阻塞状态。

图3 模型图Fig.3 Model diagram

模型建好后，移动计算空间的底面以模拟单轴压缩试验，具体步骤为：使计算空间的底面按照恒定的速度v向上(Z方向)运动，而保持其他面不动，压缩过程中输出粒间接触力信息，计算试样的宏观应力，当Z方向上的总应变量达到3%时停止。为了使颗粒体在压缩过程中保持准静态，v不能太大，取值0.005 m/s。

3 宏观应力张量的表示方法

(3)

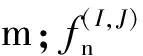
在剪切或压缩过程中，接触切向力相对于接触法向力来说，可以忽略不计(数量级倍的差别)。因此，简化平均宏观应力张量，式(3)可转变为

(4)

为了证明此结论的可靠性，分别采用式(3)和式(4)获取单轴压缩试验过程中的主应力，将式(4)和式(3)的差值与式(3)作比定义为相对误差，用Rerror表示。同时，设置多种粒间摩擦系数，μ= 0.2～0.5，以验证粒间摩擦系数是否对该结论产生影响。

由图4可知，忽略接触切向力以后，简化的平均宏观应力张量与简化前的差别甚小，在±6%以内，且摩擦系数越大，相对误差就越大。

图4 简化前和简化后平均宏观应力张量的相对值Fig.4 The relative value of the average macroscopic stress tensor before and after simplification

对于单分散颗粒体(即构成颗粒体的颗粒具有相同的直径)来说，相互接触的两颗粒形心的距离l(I,J)为

l(I,J)=Dp-δ(I,J)

(5)

式(5)中：Dp为颗粒的直径，m。由于接触的刚度参数非常大，因此颗粒间的接触重叠量相对于颗粒直径来说，可以忽略不计，因此可以得

l(I,J)=Dp

(6)

将式(6)代入式(4)可得

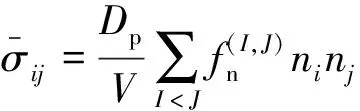
(7)

颗粒材料的孔隙率和配位数之间存在联系[9-10]，式(7)中V可采用颗粒配位数Z、颗粒体积分数ns以及颗粒接触数量Nc进行换算：

(8)

将式(8)代入式(7)可得

(9)

而在Hertz接触模型中，接触法向力的计算公式为

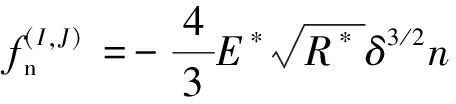
(10)

式(10)中：n为接触法向单位向量；E*和R*分别为接触的弹性模量和相对半径，计算公式为

(11)

式(11)中：EI、EJ、νI、νJ分别为相互接触的两颗粒的弹性模量和泊松比；RI和RJ分别为相互接触的两颗粒的半径。

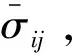
(12)

4 细观组构张量的表述方法

在荷载作用下，颗粒材料的粒间接触力分布具有不均匀性，即各向异性，是颗粒材料的特点之一。对于天然土体，土粒的形状是随机不规则的，在这种情况下，颗粒的择优定向、分支向量(连接两个相互接触的颗粒形心的向量)、孔隙定向和接触力的分布均是不均匀分布的，然而采用统计学方法可以描述它们的各向异性特点[4]。组构一词常表述的是颗粒的空间排列特点，在这里定义为接触力分布、分支向量和颗粒定向等在颗粒体中的排列特征。组构张量是组构的量化形式，常采用二阶张量形式进行描述[11-12]，即

(13)

(14)

图5展示了在轴向压缩试验中获取的接触力法向组构张量，分别采用特征值之差与特征值之比描述接触法向各向异性在压缩过程中的变化，可见，两种定义都可以很好地描述接触法向各向异性。出于简化的目的，采用式(14)表征组构张量的各向异性程度。

图5 Φ1与Φ3差值和比值在单轴压缩过程中的变化Fig.5 The difference and ratio of Φ1 to Φ3 during uniaxial compression

5 假定

为建立宏观应力与粒间接触力各向异性的联系，需作适当的假设。假设在单轴压缩试验中，与压应力作用面平行的方向上(x-y水平面)，即横向方向上，接触力向量的大小及数量分布相同，则Φ2=Φ3，且有Φ1+Φ2+Φ3=1，如图6所示。

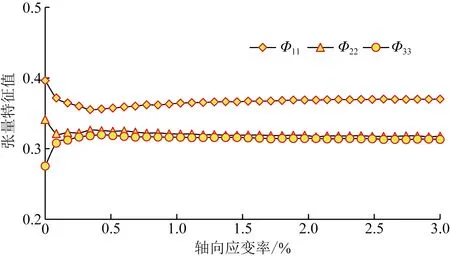
图6 单轴压缩试验过程中接触力法向组构 张量的特征值Fig.6 The eigenvalues of the normal fabric tensor of the contact force during the uniaxial compression test

6 平均宏观应力与细观组构张量的联系

宏观应力比σr和细观组构比Φr分别采用式(15)和式(16)进行计算。式(15)由式(12)推导得出，式(16)由式(13)进行推导。

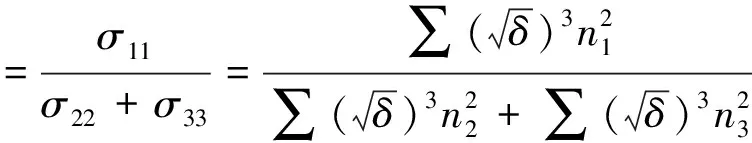
(15)

式(15)中：σ11、σ22和σ33均为宏观主应力；∑表示基于统计样本中总接触数量的求和。

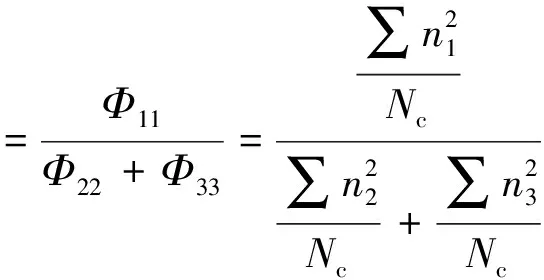
(16)

式(16)中：Φ11、Φ22和Φ33为接触法向在三维空间中3个主方向上的各向异性。

为求出宏观应力比与细观组构比的关系。首先定义两个无量纲参数, 令

(17)

图7为在改变粒间摩擦系数μ和试样体积分数ns的情况下，单轴压缩试样过程中Rσ和RΦ的变化。其中μ取值为0.0、0.01、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9，ns取值范围为0.594～0.64。图7结果表明，Rσ和RΦ具有很好的线性关系(线性拟合的相关性系数R2超过0.96)，且这种线性关系与试样中颗粒的体积分数ns有关，而与粒间摩擦系数无关μ。采用下式表征Rσ和RΦ的线性关系：

RΦ=c1Rσ+c2

(18)

式(18)中：c1和c2为与颗粒体积分数相关的参数。可见，颗粒的体积分数决定着颗粒体的相对密度，而相对密度是粒状土宏细观力学响应的主要影响因素之一。

图7 不同粒间摩擦系数和颗粒体积分数情况下 Rσ和RΦ在压缩过程中的变化Fig.7 Changes of Rσ and RΦ during compression under different inter-particle friction coefficients and particle volume fractions

同样，基于不同体积分数的单轴压缩试验结果，拟合得到c1和c2与体积分数的关系式：

(19)

需要注意的是，Rσ和RΦ在单轴压缩试验中是随着颗粒体积分数在变化的，而式(19)中c1和c2是与试样初始体积分数相关的。

根据式(14)，细观组构各向异性指标计算公式为

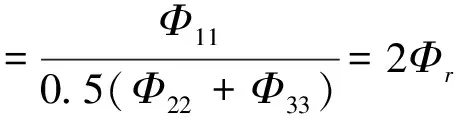
(20)

由式(20)可得，细观接触力各向异性与宏观平均应力的关系为

(21)

7 结论

土体等颗粒材料的宏观力学响应与颗粒层面细观力学行为之间的联系是现代土力学中的难点和热点之一。针对已有的宏细观本构关系多缺乏普适性的问题，根据已有理论研究成果，采用赫兹接触理论，基于颗粒流离散元程序PFC3D开展颗粒体宏观应力张量与细观接触力组构张量关系研究，提出了更具普适性的宏细观本构模型。首先对宏观应力张量进行简化，简化后的宏观应力张量与实际值的误差小于6%。然后定义了细观接触力组构各向异性指标。基于此，在假设单轴压缩横向方向上组构各向异性相同的情况下，定义了两个无量纲的参数Rσ和RΦ。多组单轴压缩试验结果表明，Rσ和RΦ具有明显的线性关系，由它们的线性关系得到了宏观应力张量与细观接触力组构张量的关系。研究成果为联系土体宏观应力与细观粒间接触力的关系提供了参考。

需要注意的是，研究结果是基于单分散颗粒体，在周期性边界条件下，单轴压缩试验中论证的，对于多分散颗粒体和更复杂的边界情况，则需要进一步研究。