光伏电站机电暂态实用化等值建模方法
2022-02-18高剑毕悦杨亚兰张梅
高剑, 毕悦, 杨亚兰, 张梅
(1.国网四川省电力公司调度控制中心, 成都 610041; 2.国网四川综合能源服务有限公司四川电力工程分公司, 成都 610072; 3.中国电力科学研究院, 北京 100192)
受限于自然资源分布特点,四川电网内大部分光伏电站分布于电网网架较为薄弱的阿坝州、甘孜州等边远地区。在此种新能源装机局部占比高,且网架薄弱的电网进行方式计算和安全稳定评估时,若仍采用单机倍乘的典型参数及简化模型进行机电暂态仿真分析,则可能出现临近线路功率振荡、新能源送出受限等问题。光伏发电相较于常规同步机组,具有单机容量小,光伏阵列数量庞大且控制分散的特点,若将每台逆变器都详细建模,势必会极大加重电力系统全域仿真的运行负担[1-3],因此亟需建立能准确反映光伏电站实际运行特性的场站级机电暂态模型,以满足大电网仿真分析的要求[4-6]。
现有研究多针对光伏发电系统进行逆变器详细建模及参数辨识[7-9],对于光伏电站场站级建模方法,文献[10]考虑光照、温度等外界环境不确定性因素对光伏电站出力的影响,通过潮流计算和光伏特性方程交替迭代,建立了光伏电站稳态等值模型,但其未对光伏电站进行暂态建模,不能反映出其在故障工况下的响应特性。文献[11]提出了光伏电站场站级机电暂态整体模型,并基于临近高压输电线路人工短路试验进行了模型验证,但所采用的验证方法会对电网造成较大冲击,对于四川电网内的网架薄弱地区并不适用。文献[12]采用设置阈值方式进行光伏逆变器实时在线聚类分群,并根据每次分群结果进行场站级迭代等值,虽能较好地反映光伏电站实际运行工况,但在大电网仿真计算时其等值过程太过复杂,不能满足工程实用性要求。
鉴于此,为兼顾光伏电站实际运行特性和电网安全及仿真压力,现提出利用光伏场站提供的各型号逆变器低电压穿越型式试验结果及场站内自动发电控制(automatic generation control,AGC)有功功率调节试验数据,进行光伏逆变器单体建模及参数辨识。再基于场站内主变、箱变、集电线路、及静止无功发生装置(static var generator,SVG)的实测电气参数搭建光伏电站场站级详细机电暂态模型,在扰动情况下运用综合距离指标Dij对各光伏方阵进行分群聚类,并基于Dij计算结果利用等值前后并网点输出功率不变原则求取集电线路等值参数。最后基于电力系统分析综合程序(power system analysis software package,PSASP)仿真平台搭建川西电网某光伏电站详细模型及等值模型,对比等值前后并网点的稳态及暂态外特性,以证明所提等值建模方法具有较好的准确性和工程实用性。
1 光伏发电单元建模
1.1 光伏阵列简化模型
根据光伏电池产生机理,假设环境温度保持不变,可得到仅考虑辐照度变化影响下光伏阵列在最大功率追踪点处输出功率PMPPT的简化数学模型[13]:
PMPPT=Vm_stdln(e+βΔS)Im_std(ΔS+1)
(1)
式(1)中:Vm_std和Im_std为标准测试环境下(温度为25 ℃,光照强度为1 000 W/m2)的最大功率点电压及电流,其值由厂家提供;e为自然对数;β为光强补偿系数,硅电池一般取0.5;ΔS为日照变化后的修正系数。
(2)
式(2)中:S为实际辐照度;Sref为标准测试环境下的辐照度。
结合式(2)进一步化简式(1),得
(3)
机电暂态建模时,稳态初始辐照度S0由潮流设定功率值P0根据式(3)折算得到,光照强度变化由暂态扰动ΔSdis确定。同时在最大功率PMPPT输出时考虑备用系数Krp,可得光伏阵列正常运行状态下的有功输出Pm,其简化模型如图1所示。
1.2 逆变器参数辨识
按照国家相关标准规定,并网光伏电站需具备正常运行时按调度AGC指令正确调节有功功率和故障情况下实现低电压穿越的能力[14]。故采用基于有功功率控制及低电压穿越试验的实测数据进行逆变器参数拟合。
1.2.1 基于有功控制能力的稳态参数辨识
机电仿真建模中,忽略逆变器作为电力电子器件的开关特性及脉冲宽度调制(pulse width modulation,PWM)等多个环节,有功控制采用比例积分控制(proportional plus integral control,PI)其详细模型如图2所示。
稳态运行时,逆变器等效于一个受控电流源,参考电网电压计算相角后,输出电流IPV为
IPV=(Ipcosθ-Iqsinθ)+ j(Ipsinθ-Iqcosθ)
(4)
式(4)中:Ip、Iq分别为有功、无功电流目标值;θ为并网点处交流电压与电流间的相位角。
有功调节时,无功电流解耦控制并无变化,则有
ΔIPV=ΔIp(cosθ+jsinθ)=ΔIp∠θ
(5)

Pe为输入信号包括逆变器实测有功;Pord为场站级有功指令;Pm为光伏方阵最大出力;输出信号Ip为有功电流目标值;Tm为描述逆变器信号采样延迟的一阶惯性环节时间常数;Tpord为响应时间;Pmax、Pmin、dPmax、dPmin分别为有功功率及有功功率变化率上下限;Pref为有功功率参考值;Kp_p和Kp_i为有功比例-积分控制 器参数图2 光伏逆变器有功控制模型Fig.2 Active power control model of photovoltaic inverter
若忽略光伏电站各逆变器实时发电能力的细微区别,在接收到AGC有功调节指令后,依据变化量均分的原则分配给所属逆变器,可认为实测场站高压并网点处的有功控制能力即代表了各逆变器对有功功率调节的响应特性。同时由于光伏电站有功控制现场试验时按照阶跃形式调节场站级有功指令值[14],故可将每次有功阶跃的指令变化量ΔPord及测量变化量ΔPe作为输入,并网点交流电流变化量ΔIPV作为输出,利用最小二乘估计法辨识得到式(5)所示PI控制关键参数Kp_p及Kp_i[15]。
1.2.2 基于低电压穿越能力的暂态参数辨识
电网由于短路故障造成电压跌落期间,光伏逆变器由于类型及控制策略不同,其低电压穿越暂态特性具有明显差异。在低电压穿越期间,逆变器控制逻辑会由正常功率控制模式切换到故障穿越模式。为准确复现实际逆变器暂态过程,低穿期间逆变器有功及无功电流均采用指定电流控制方式。
有功电流指令值为
IP_LVRT=K1P_LVVt+K2P_LVIP0+IPset_LV
(6)
式(6)中:IP0为初始有功电流;Vt为端电压幅值;K1P_LV为有功电流计算系数1,可根据电压跌落深度调节有用电流输出大小;K2P_LV为有功电流计算系数2,反映初始有功在故障穿越过程中所占比重;IPset_ LV为有功电流设定常数,决定有功输出最低阈值。
无功电流指令值为
IQ_LVRT=K1Q_LV(Vin-Vt)+K2Q_LVIQ0+IQset_LV
(7)
式(7)中:IQ0为初始无功电流;Vin为进入低穿的电压阈值,一般取0.9;K1Q_LV为无功电流计算系数1,根据电压跌落深度正向调节无功电流输出大小;K2Q_LV为无功电流计算系数2;IQset_LV为无功电流设定常数,决定无功输出最高阈值。
针对式(6)和式(7)中低穿控制关键参数,仍采用最小二乘估计法辨识得到。同时还要重点关注故障结束后逆变器有功输出的恢复能力,其恢复速度至少应达到30%额定功率每秒[14],可结合低穿试验有功恢复曲线拟合确定恢复斜率或惯性常数。
2 光伏电站等值建模
2.1 场站级详细模型搭建
由于在电网薄弱地区进行光伏电站并网高压侧人工短路试验具有较大安全隐患且造价较高,不利于工程推广,故提出在准确建立光伏发电单元单体模型后,依照光伏电站集电系统详细电气接线图,场站实测集电线路导线型号及长度、箱变电气参数、主变压器电气参数、无功补偿装置电气参数、设备及电站保护参数、外部电网短路容量等实际信息,搭建包含电站内所有光伏发电单元及电气设备的详细场站级模型,作为等值模型是否准确的有效验证。
2.2 基于综合距离指标的聚类分群
机电暂态建模重点关注光伏电站受到接地故障等大扰动后的动态特性,由于集电系统电压分布的影响,场站内接入不同箱变的光伏发电单元在故障前后表现出的运行特性具有一定差异[16-17]。将同一箱变下两光伏发电单元作为一光伏阵列,选取故障前后各箱变高压侧电压动态响应轨迹差异最小作为聚类目标。
定义故障发生前后,各光伏阵列电压动态特性综合距离指标Dij为
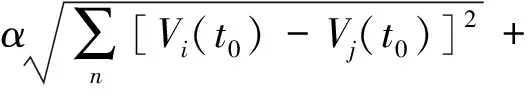
(8)
式(8)中:Vi(t0)、Vj(t0)分别为光伏阵列i、j故障发生前稳态电压标幺值;ΔVi(t)、ΔVj(t)为光伏阵列i、j故障发生后暂态电压跌落标幺值;α为权重系数,根据仿真曲线对比稳态及暂态电压差异大小作出调整,初始可取0.5;n为光伏阵列总数。
Dij依据欧式距离综合选取各光伏阵列稳态及暂态电压变化程度,准确刻画出各逆变器在故障前及期间的动态轨迹整体相似度。按照Dij定义,进而基于详细模型故障仿真,计算出各光伏阵列两两间的综合距离指标值,实现整场站的聚类分群。
2.3 等值模型参数计算
对光伏电站详细模型进行等值建模时,由于已基于2.2节综合距离指标按照动态特性相似实现光伏阵列划分,故对等值后的光伏发电单元采用容量倍乘的方式进行功率聚合,箱变相关参数按照分群结果根据原始串并联关系折算得到。集电系统一般为35 kV及以下电压等级且多采用电缆进行电能汇集,其单位对地电容值远大于架空线路[18],不能忽略其对整个光伏电站暂态特性的影响。
鉴于此,基于场站详细模型,采用等值前后光伏电站并网点输出功率不变原则求取集电线路等值参数。等值后集电线路模型如图3所示。
根据详细模型仿真得到待等值线路功率损耗为
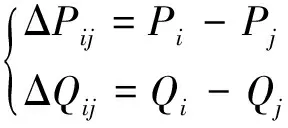
(9)
按图3所示的等值电路,待等值集电线路功率损耗为

(10)
式(10)中:Pi、Qi基于详细模型仿真得到。

i侧和j侧分别为分群后待等值的首、尾光伏阵列箱变高压侧;及分别为i侧和j侧电压、有功功率、 无功功率;R为线路等值电阻;X为等值电抗图3 光伏电站集电线路等值电路Fig.3 Equivalent circuit of photovoltaic station collector lines
为使光伏电站高压并网点等值前后外特性一致,需满足各段等值线路功率损耗不变。基于综合距离指标Dij分群后,各光伏方阵电压稳态及暂态特性均相似,故可假设待等值集电线路各点电压相等,均取为Vi,再将式(9)两变量值代入式(10),求得线路等值电阻R及等值电抗X。
3 仿真验证
3.1 算例等值参数求取
基于所提场站级等值建模方法,以川西牧区电网某实际光伏电站为例,搭建可应用于大电网方式计算及规划分析等场景的机电暂态等值模型。该光伏电站总装机容量30 MW,SVG额定补偿容量为感性11 Mvar至容性11 Mvar。光伏逆变器为额定功率500 kW的集中式逆变器,出口电压315 V并以“两机一变”扩大单元接线方式经箱变升压后并入35 kV集电系统。全站共计30个容量为1 MW的光伏方阵,通过3条汇集线路并入光伏电站110 kV升压站低压侧。光伏电站集电系统详细电气接线图及站内设备参数分别如图4和表1所示。
经最小二乘法辨识得到光伏逆变器正常运行时有功控制PI参数为Kp_p=0.148,Kp_i=3.36。电压低穿期间有功功率及无功功率控制参数分别为:K1P_LV=0.46,K2P_LV=0.21,IPset_ LV=0.08;K1Q_LV=2.85,K2Q_LV=1.04,IQset_LV=0.03;故障结束后有功采用定斜率方式恢复,恢复斜率为5.43 p.u./s。单体参数辨识完成后,计算各光伏阵列综合距离指标
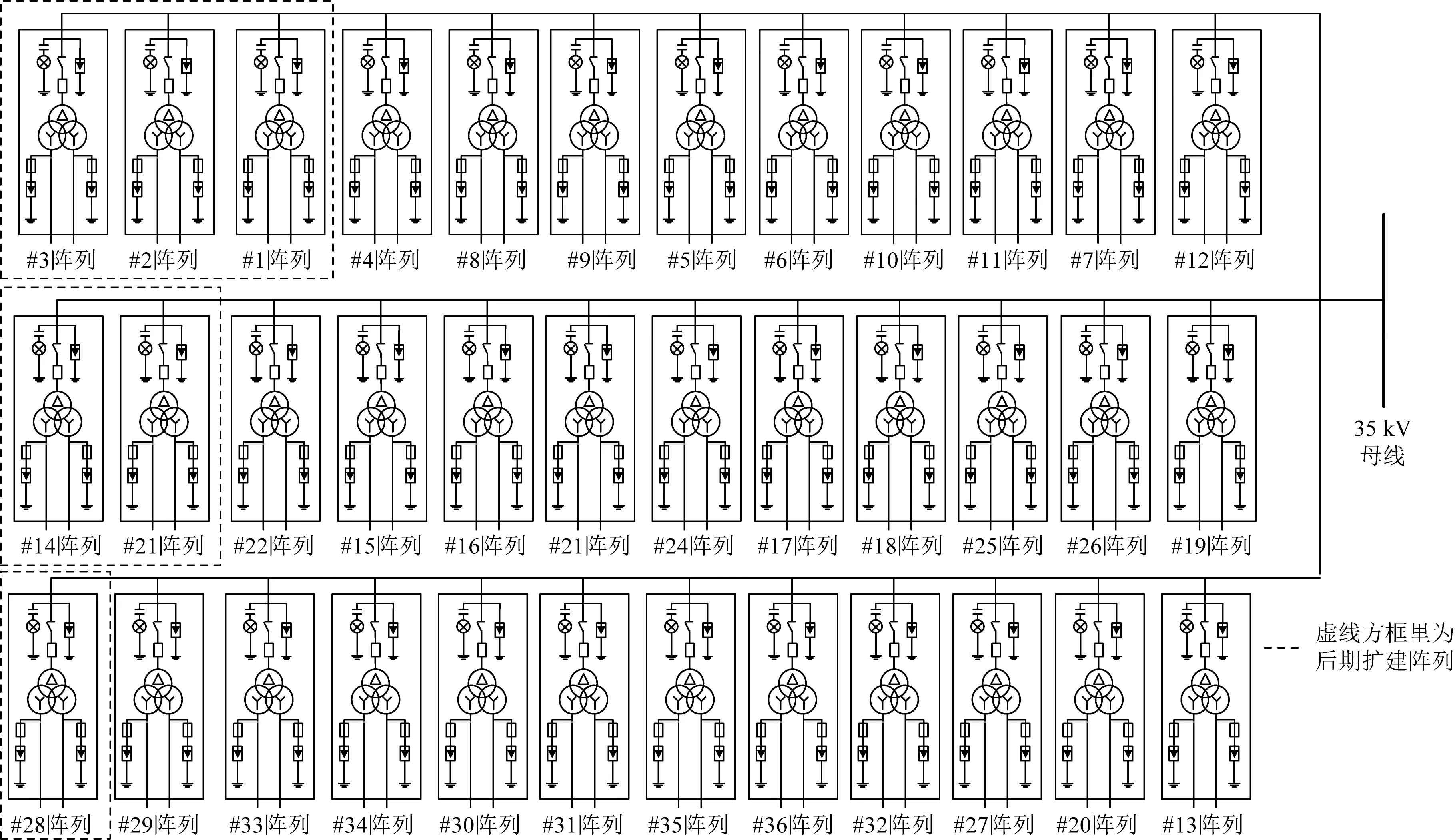
图4 光伏电站集电系统电气接线图Fig.4 Electrical wiring diagram of photovoltaic power station collection system
Dij,光伏方阵两两间的Dij计算结果如图5所示。
按图5所示Dij分布结果,取参考阈值0.001,将原光伏阵列等值为2个光伏方阵,#20、#27、#29~#36为一等值机群,其他阵列为另一机群。等值后该光伏电站基于PSASP的仿真模型如图6所示,场站内各项等值参数如表2~表4所示。

表1 变压器电气参数Table 1 Transformer electrical parameters
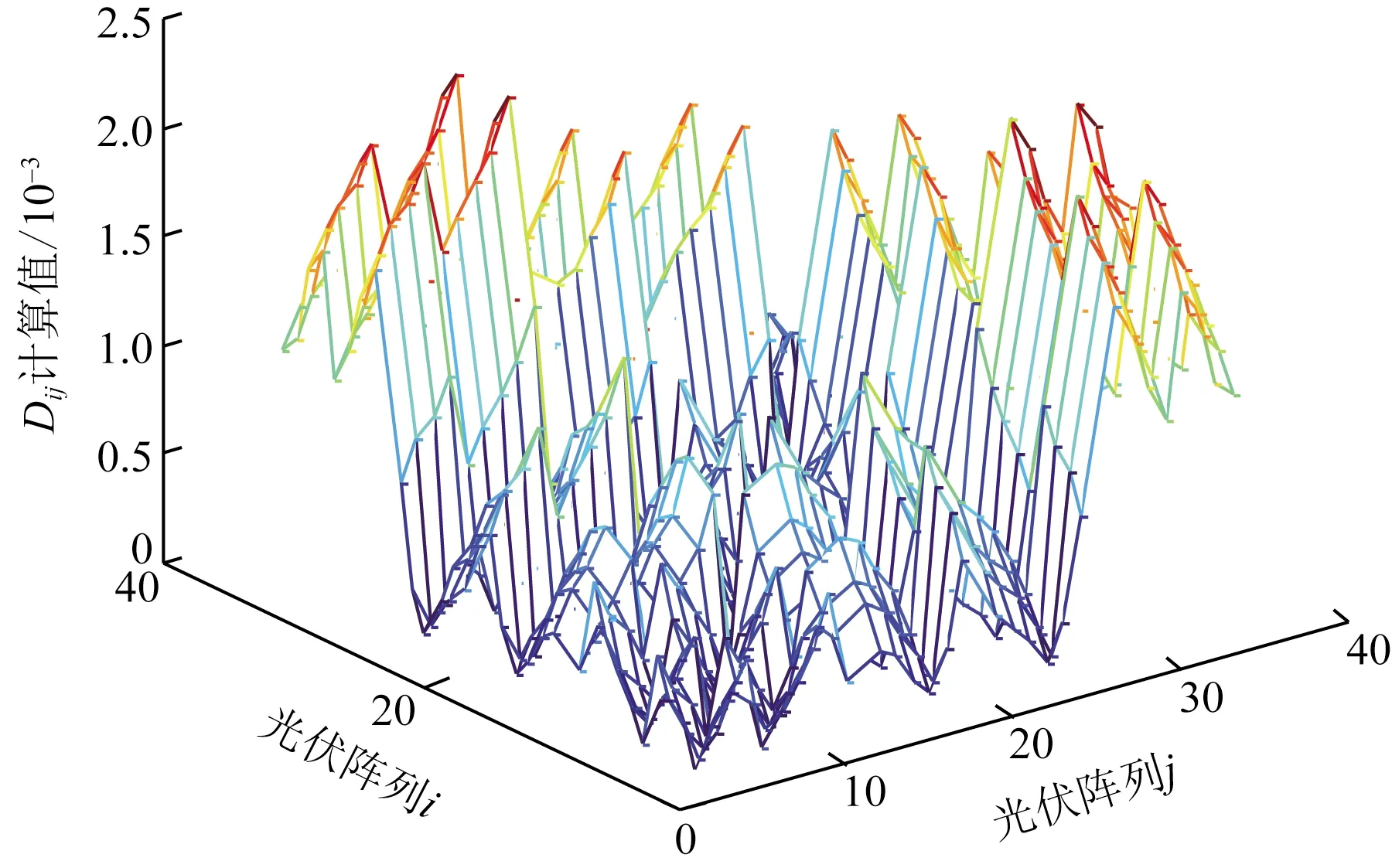
图5 光伏阵列Dij计算结果分布图Fig.5 Distribution of Dij calculation results within photovoltaic array
3.2 额定出力三相接地故障
为验证等值模型与详细模型暂态特性的准确程度,当光伏发电单元额定出力时,0.5 s在光伏电站110 kV高压并网点施加三相接地故障,故障持续0.1 s,使电压跌落到0%额定电压Vn,对比等值模型与详细模型电压、电流、有功及无功仿真波形,如图7所示。各波形图均以标幺值标注,基准值取电压VB=110 kV,功率SB=100 MVA。
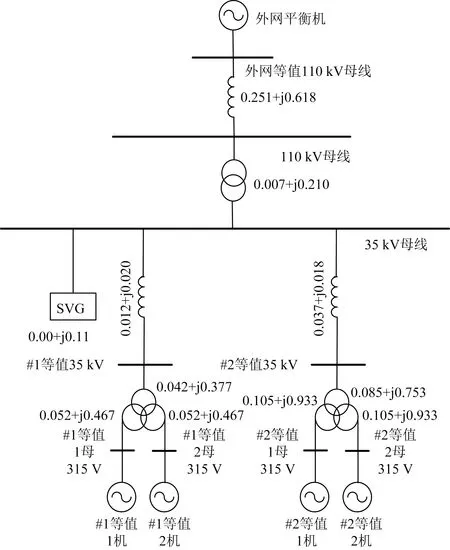
图6 光伏发电站等值模型示意图Fig.6 Schematic diagram of equivalent model of photovoltaic power station

表2 等值机组基础参数Table 2 Basic parameters of equivalent unit

表3 发电单元变压器基础参数Table 3 Basic parameters of power generating unit transformer

表4 等值线路阻抗参数Table 4 Impedance parameter of equivalent line
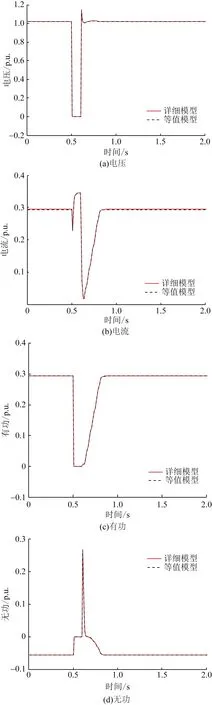
图7 电压跌落到0% Vn时等值模型与详细 模型仿真对比Fig.7 Simulation comparison of equivalent model and detailed model when voltage drops to 0% Vn
由图7仿真结果可知,所建立的等值模型和详细模型在典型三相接地故障时对外电网表现出的暂态响应基本相同,具有很好的一致性。同时仿真对比了两模型在三相及单相接地故障电压分别跌落到20%Vn、40%Vn、60%Vn、80%Vn的多种故障情况,仿真结果均表明等值模型能较好复现详细模型的暂态特性,鉴于篇幅仿真波形在此不再给出。
3.3 AGC有功功率调节
3.2节验证了等值模型与详细模型的暂态准确性,本节基于光伏电站并网性能试验中AGC有功功率调节现场录波数据,进一步对比等值模型与电站实际有功控制特性的拟合程度,图8为对比波形图。有功功率控制试验在1 min处下发有功调节指令,从60%Pn上升到80%Pn,考虑指令下发延迟时间及控制调节时间,现场实际响应时间为14.1 s。
由图8可知,等值模型与实测数据在响应速度上保持了较好的一致性,且调节到目标功率值后稳态最大偏差为控制指令值的0.83%,具有较满意的等值精度。
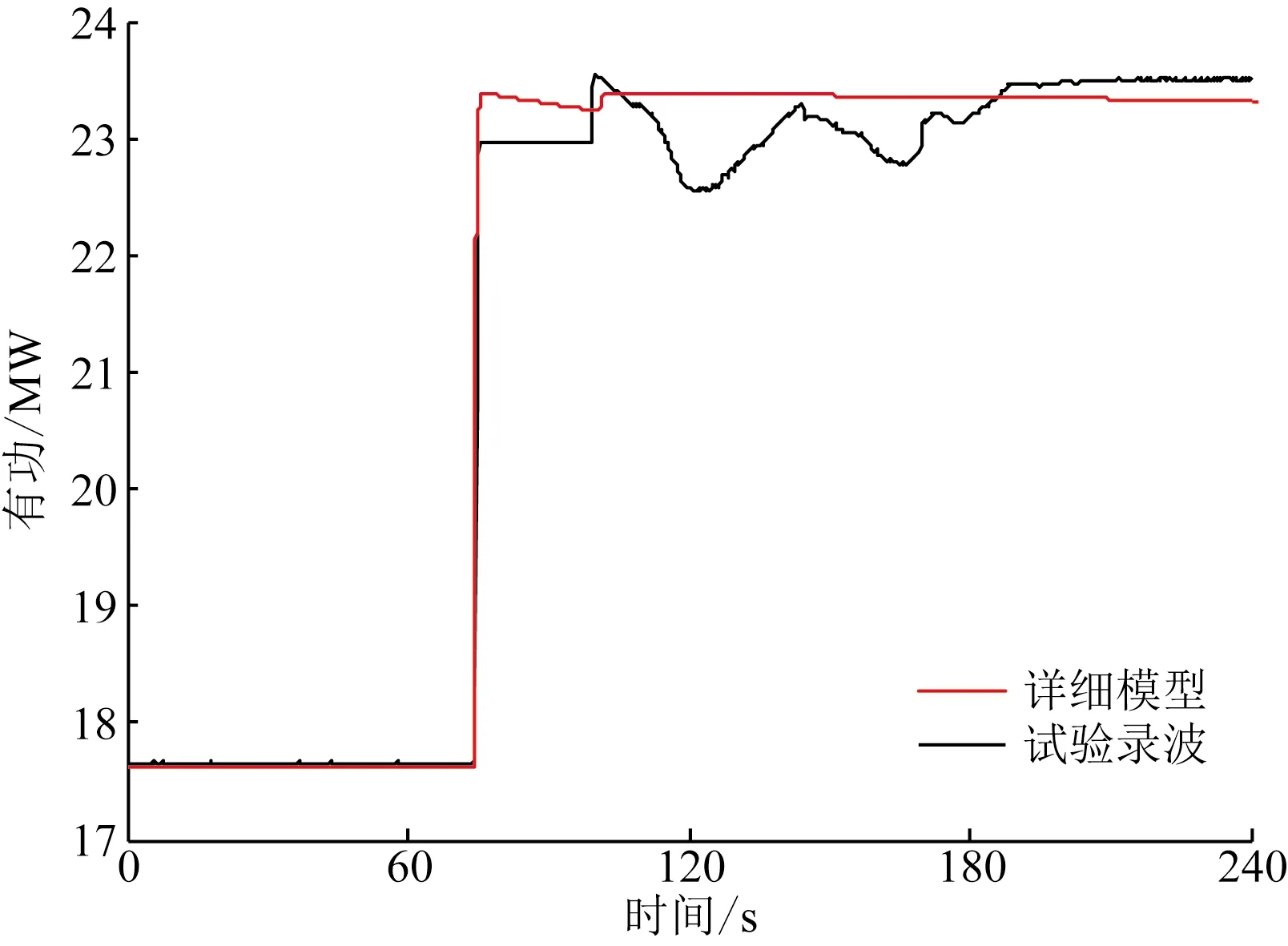
图8 AGC有功调节时等值模型与实测数据对比Fig.8 Comparison of equivalent model and measured data during AGC active power adjustment
4 结论
(1)所提等值方法综合考虑光伏电站实际运行特性与建模可实现性,基于单体实测参数辨识、详细模型搭建、光伏阵列集群划分及等值参数聚合4个步骤,完成光伏电站场站级等值建模工作,兼顾了大电网机电暂态仿真准确度要求及工程实用价值。
(2)后续可根据最新国标要求,采用光伏电站一次调频及高电压穿越等试验的实测参数,持续更新仿真模型中的相关控制参数,进一步完善等值模型的整体机电暂态特性。
