中洞法连拱隧道施工稳定性分析及优化

徐波， 杨旺兴， 李加加， 刘涛影， 张朝阳

(1.中铁建华南建设有限公司， 广州 511458； 2.中铁十六局集团北京轨道交通工程建设有限公司， 北京 101100； 3.中南大学资源与安全工程学院， 长沙 410083)

近年来，随城市轨道交通事业的蓬勃发展，地铁线路及车站的数量快速增加，据统计仅广州市现有运行地铁线路14条，在建线路11条，地铁站更是多达213座。密集度增加导致一些车站施工时需规避对既有建筑及地面交通的影响，施工方法也由传统明挖基坑向暗挖、明暗挖结合转变，开展暗挖段的施工稳定性研究对于工程安全至关重要。中国自1995年在白云山隧道中首次使用双连拱结构后，连拱隧道的使用及相关研究迅速增多[1]。朱毅飞[2]研究了中洞法中立柱施作时机对车站开挖力学效应的影响，得出Ⅳ、Ⅴ级围岩条件下及时施作中立柱能有效减小开挖扰动。牛牟[3]采用有限元分析软件，研究了浅埋偏压连拱隧道施工力学行为，提出采用扩大中导洞尺寸并偏移中隔墙浇筑位置的方法缓解中隔墙偏压现象。Tuneyoshi等[4]通过分析200多个大断面连拱隧道模型，研究了隧道跨度、开挖形式、地质条件、隧道埋深等因素对隧道稳定性的影响。宋战平等[5]研究台阶法施工不同台阶错距下隧道施工的动态力学响应特征，分析了不同错距下支护结构变形特点。井洪涛[6]通过埋设地层变位和围岩应力测试元件，分析了浅埋大跨度隧道开挖过程支护结构变形、地表沉降及围岩应力变化规律。左双英等[7]基于剪切滑移线理论，计算了中导洞+台阶法施工初支结构在剪切区所提供的支护抗力。王昊统等[8]根据相似理论，采用自制室内三维模型实验系统对地铁隧道动态开挖过程进行模拟，总结了不同工况下的地表沉降规律。

基于此，现以广州大道中站为依托，研究中洞法连拱隧道施工过程中隧道拱顶沉降、底部变形、洞周收敛、初支结构应力、中隔墙应力以及地表沉降的动态响应特征，总结不同工艺参数下隧道变形规律，通过与现场监测结果比对，以期为暗挖车站施工提供了理论指导，并为类似工程提供借鉴。

1 工程概况

广州大道中站为广州地铁十号线自南向北第二座车站，地下3层14 m岛式站台，采用明暗挖结合施工，暗挖段设计里程为：ZDK8+291.152～ZDK8+377.152，长86 m，隧道断面宽24.86 m，高11.24 m，埋深21.17 m(图1)。暗挖段地层由上至下依次为：填土层、可塑状粉质黏土层、全风化碎屑岩层、强风化泥质粉砂岩层以及微风化泥质粉砂岩层。暗挖隧道采用中洞+交叉中隔壁法(cross diaphragm，CRD)施工，中洞采用三台阶法施工，由上至下台阶高度为4.8、2.7、1.1 m，侧洞采用CRD法开挖。超前支护采用超前小导管，侧墙打设系统砂浆锚杆、全断面格栅钢架+临时型钢支撑组成联合支护体系。

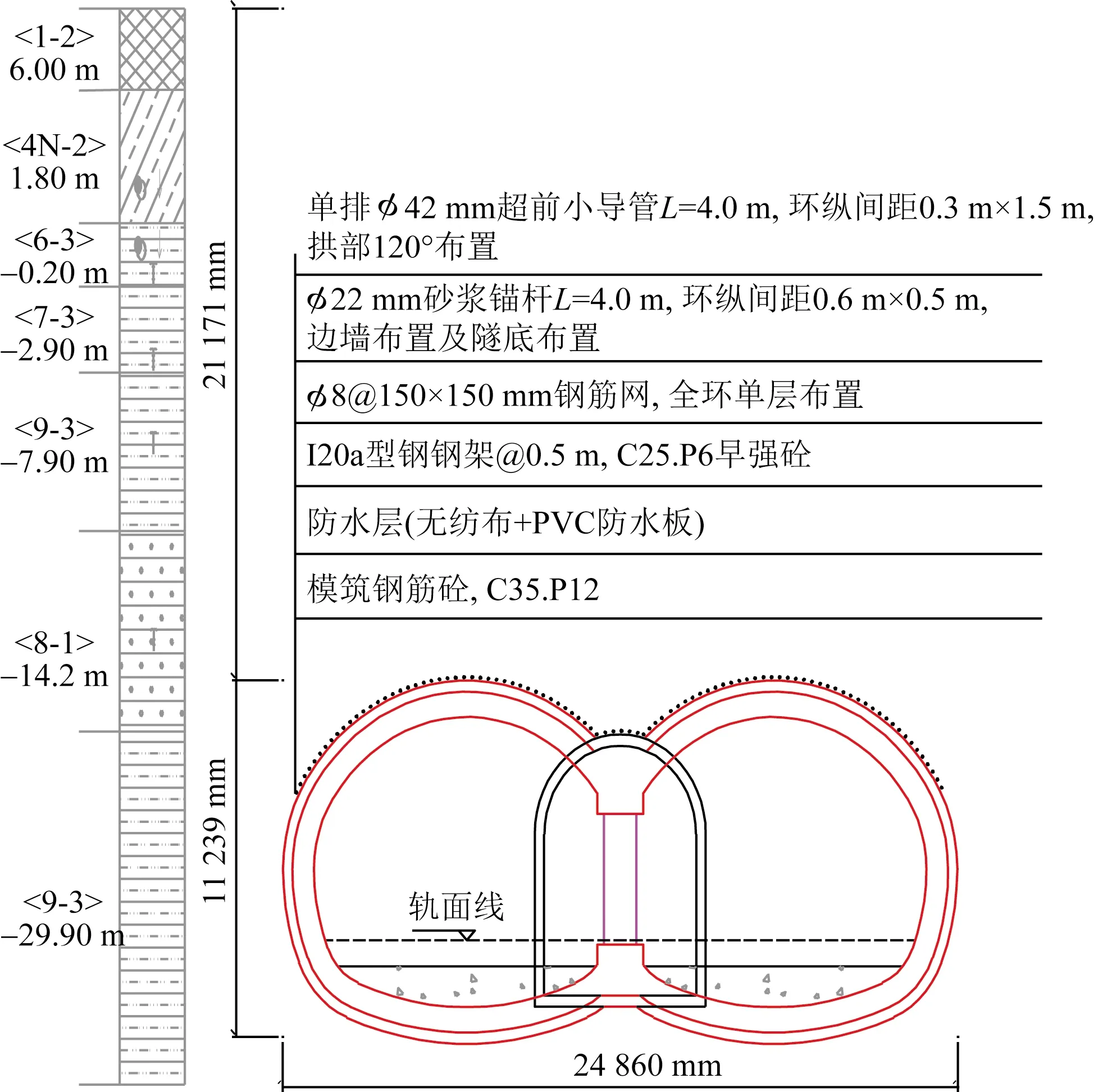
图1 连拱隧道断面图Fig.1 Cross-section of double-arch tunnel

2 数值模型构建

为研究隧道施工过程中隧道结构受力、变形规律以及对周边地层的影响，构建了的长60 m的双连拱隧道模型，如图2所示。考虑边界效应的影响，隧道左右围岩各取3倍洞径宽度，隧道至模型底部边界为3倍洞高[9]，最终模型尺寸为175 m×60 m×65 m。模型中围岩及隧道中隔墙采用实体单元，初支结构及临时钢支撑采用板单元，根据等效原则将超前小导管及系统锚杆加固的围岩视为加固圈，通过提高加固圈围岩的物理力学参数实现加固处理，最终模型划分6.9万个单元，地层及支护结构物理力学参数如表1所示。模型底部边界设置竖向位移约束，四周限制法向位移，上表面为自由面，计算荷载考虑围岩自重。

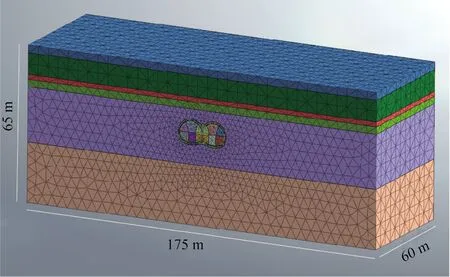
图2 连拱隧道模型Fig.2 Double-arch tunnel model

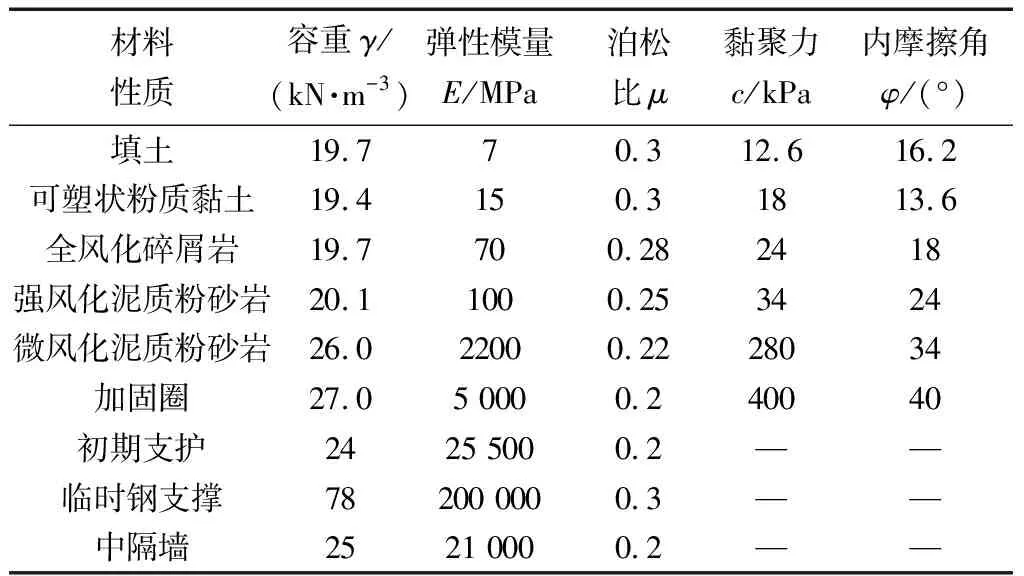
表1 地层及支护结构物理力学参数Table 1 Physical and mechanical parameters of stratum and supporting structure

3 连拱隧道稳定性分析

3.1 隧道变形分析

3.1.1 测点布设

根据实际施工情况，利用“钝化”与“激活”功能模拟了中洞法暗挖隧道的开挖与支护，并分别用①～⑦对各开挖部位进行了标号，其中，中洞台阶法开挖上下台阶错距15 m；侧洞CRD法施工，相邻台阶错距5 m；先行洞与后行洞拉开距离为10 m。为充分了解不同施工阶段隧道变形情况，分别沿隧道走向0 m(洞口)、30 m及60 m布置监测断面，分析隧道拱顶下沉、底部变形以及洞周收敛情况，测点布设如图3所示。

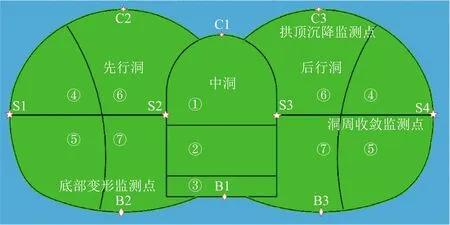
图3 隧道变形监测点Fig.3 Monitoring points of tunnel deformation

3.1.2 拱顶沉降变形

分别在中洞、先行洞以及后行洞拱顶布置沉降测点获取中洞法隧道施工过程中拱顶沉降曲线(图4)。图4(a)为中洞拱顶沉降曲线，洞口(0 m)位置的曲线变化显示，施工阶段1～4中洞上台阶的开挖导致拱顶快速下沉，此阶段下沉量达到1.40 mm，中、下台阶的开挖对拱顶下沉影响较小，仅产生约0.39 mm的沉降，在下台阶掌子面远离洞口5 m后，沉降值基本维持在1.79 mm，分析认为，上台阶开挖卸荷作用导致一部分地应力得到释放，因此中下台阶开挖影响相对较小。施工阶段23～25先行洞远离中洞侧台阶④、⑤的开挖对中洞拱顶沉降影响较小，而施工阶段26、27靠近中洞侧台阶⑥、⑦的开挖则会导致中洞拱顶再次产生快速下沉，施工阶段30以后曲线再次向下偏转，原因在于后行洞⑥、⑦台阶的开挖导致拱顶沉降速度加快，且整个曲线该段斜率最大，表明该阶段拱顶沉降速度最快，因此该节点施工应该加强对拱顶沉降速度的监测。随后行洞逐渐远离洞口位置，中洞拱顶沉降速度放慢并最终稳定在了4.79 mm。30 m与60 m处的沉降曲线与0 m处相似，在掌子面临近测点5 m位置拱顶开始下沉，下台阶掌子面远离洞口5 m后沉降维持稳定。60 m监测曲线在Step 13出现了明显沉降，此时中洞上台阶贯通隧道，隧道轴线方向失去围岩支撑，作用在支护结构上的地应力增大。

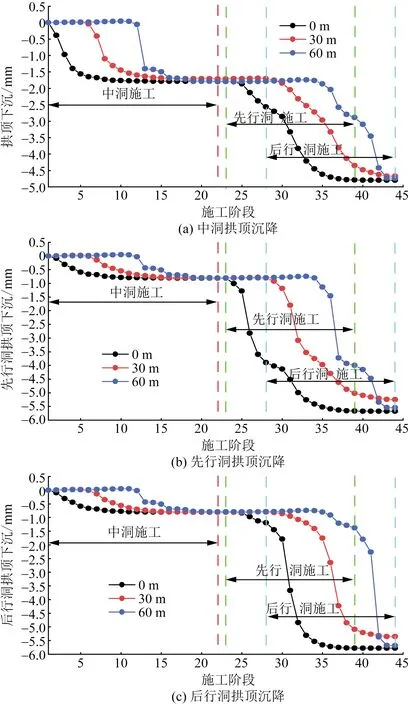
图4 隧道拱顶沉降变形曲线Fig.4 Settlement deformation curve of tunnel vault

图4(b)中先行洞拱顶沉降曲线表明，中洞开挖虽然也会造成侧洞拱顶沉降，但影响相对较小，中洞开挖过程中侧洞仅产生了约0.8 mm的沉降。三条曲线均具有快速下降的阶段，其中0 m测点在施工阶段25～27下沉2.32 mm，30 m测点在施工阶段30～32下沉1.89 mm，60 m测点在施工阶段36～38下沉2.47 mm，这些阶段均对应着先行洞靠近中洞方向台阶⑥、⑦的开挖，分析认为远离中洞方向台阶④、⑤开挖导致应力集中在围护结构及⑥、⑦台阶上，随台阶⑥、⑦开挖应力进一步被转移到支护结构上，因此拱顶产生了较大变形。图4(c)后行洞沉降曲线快速下降阶段发生在后行洞⑥、⑦台阶开挖过程中，此时整个隧道断面形成导致临空面急剧增大，故沉降变化量更大，60 m测点仅在施工阶段41～42一个阶段便产生了3.11 mm的沉降，因此在后行洞即将贯通时需要加强拱顶日变形量的监测并及时封闭成环。后行洞施工完成后最大沉降值达5.78 mm。

3.1.3 隧道底部变形

隧道底部变形如图5所示。整个开挖过程中洞底部变形曲线呈上凸型，图5(a)所示，中洞开挖卸荷导致隧道底部地应力向上推挤中洞底面，故随中洞开挖其底部隆起值不断增大。30 m监测曲线显示在上台阶距离测点5 m位置(施工阶段6)隆起值开始增大，下台阶掌子面远离测点约5 m后(施工阶段14)稳定在1.64 mm。侧洞的开挖导致底部应力集中区域向侧洞发生转移，且中隔墙上压应力的不断增大使其对底部隆起的抵制作用增强，故随侧洞施工中洞底部隆起开始回落。两侧洞底部变形曲线形态相似，隆起主要发生在该侧侧洞施工过程中，且测点5 m范围内岩层开挖时产生了最大的隆起变形量，先行洞在1.58～1.90 mm，后行洞在1.78～2.22 mm。图5(b)中在掌子面远离测点后测点的隆起值略微减小。图5(c)中在掌子面到达测点之前测点隆起值先出现了降低，这归因于先行洞与后行洞的相互影响，先行洞与后行洞开挖导致应力向正在施工侧转移，因此临近测点部位正在施工侧拱底隆起值增大，而未施工侧隆起值减小。侧洞底部隆起最大值在60 m处，先行洞最大隆起量为2.39 mm，后行洞最大隆起量为2.46 mm。

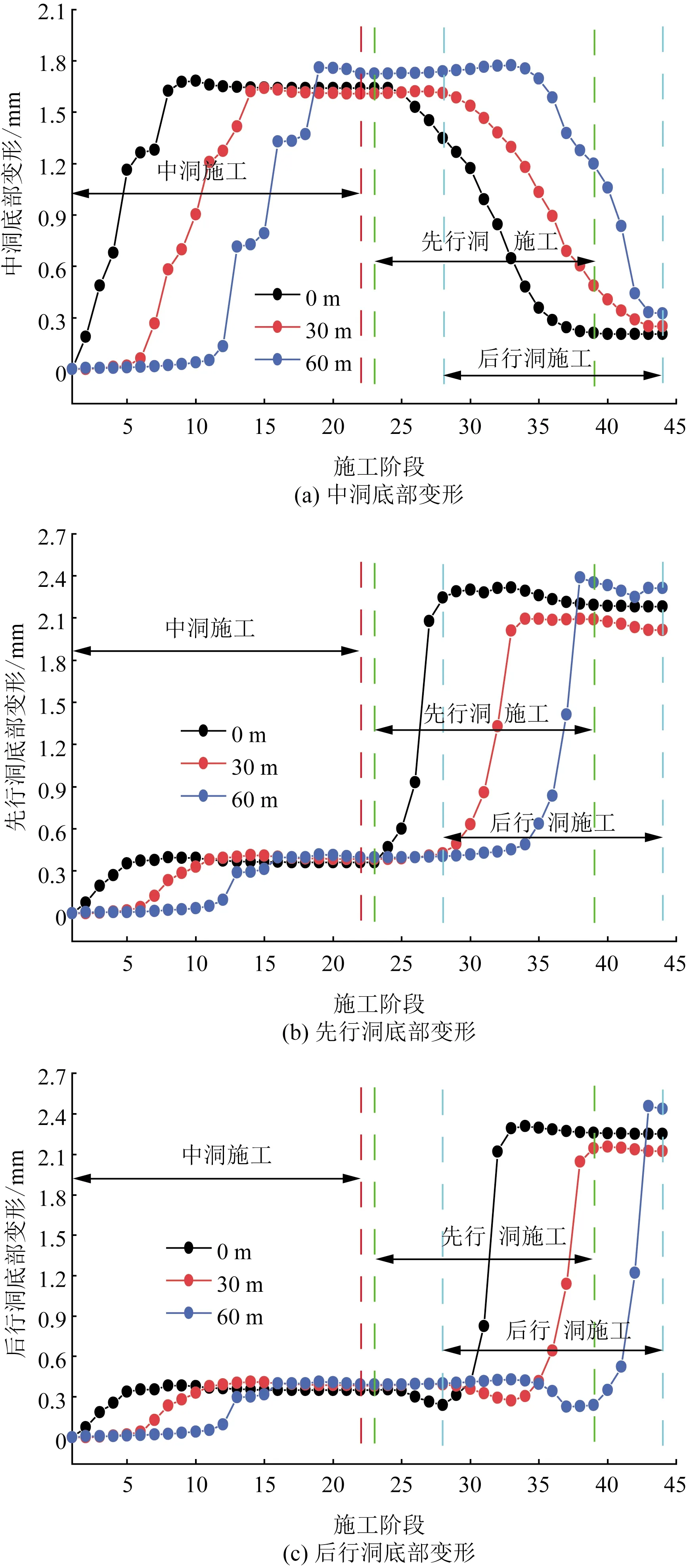
图5 隧道底部变形曲线Fig.5 Deformation curve at the bottom of the tunnel

3.1.4 洞周收敛变形

图6为中洞法隧道开挖过程中各硐室收敛变形情况，默认以向洞内收敛为正。中洞开挖导致中洞侧壁失去支撑，地应力在中洞附近聚集并向洞内挤压侧壁，而侧洞施工在释放中洞侧壁围压的同时增大了中洞拱顶压应力，导致中洞侧壁向外鼓胀，因此中洞收敛变形先增大至0.88 mm而后逐渐减小至-1.69 mm。先行洞与后行洞的洞周收敛变形趋势较为一致，收敛值均随侧洞开挖先逐渐增大而后保持稳定，开挖完成时先行洞与后行洞的收敛值分别为1.59 mm和1.41 mm。

3.2 支护结构受力分析

通过数值模拟手段可以获取连拱隧道支护结构上的应力分布状态(图7和图8)，隧道开挖完成后侧洞台阶⑥、⑦部位均出现了拉应力[图7(a)]，且上台阶初支结构受拉特征更为明显，达到1.59 MPa。压应力则主要集中在侧洞台阶④部位[图7(b)]，该部位的压应力最大可达4.40 MPa。相较而言，侧洞台阶⑤部位在支护结构中受力最小。整个支护体系中，无论是最大拉应力还是最大压应力均分布于钢支撑上，最大拉应力分布在侧洞远离中洞方向的横向钢支撑上[图8(a)]，最大值达到4.27 MPa，最大压应力分布在侧洞纵向钢支撑上[图8(b)]，最大值达到12.62 MPa，钢支撑的选材及施工必须严格按照设计要求，保证施工质量。

3.3 中隔墙应力转换分析

中隔墙作为暗挖隧道的永久支护结构，分析施工过程中中隔墙内部应力转换，并对薄弱部位进行加强，对隧道的安全稳定具有重要作用[10]。侧洞开挖过程中中隔墙上应力分布状态如表2所示，先行洞开挖在中隔墙底部以及顶部偏向先行洞方向均出现了0.57 MPa的拉应力，在中隔墙的中部、底部以及顶部偏向先行洞方向出现了0.91～2.38 MPa的压应力。随后行洞开挖，偏压现象逐渐消失，施工阶段 28时拉应力主要集中在中隔墙顶部两角及底部区域，最大值达到1.3 MPa，整个中隔墙均分布有压应力，顶底部在0.95～1.89 MPa，中部在1.89～5.27 MPa。侧洞开挖完成后，中隔墙内部应力分布同施工阶段28相似，但应力值增大，此时中隔墙内部最大拉应力为1.79 MPa，最大压应力为7.09 MPa。总的来说，施工过程中中隔墙中部主要承受压应力，而顶纵梁和底纵梁则同时承受拉应力和压应力，因此施工过程中要严格保证顶纵梁和底纵梁的施工质量。

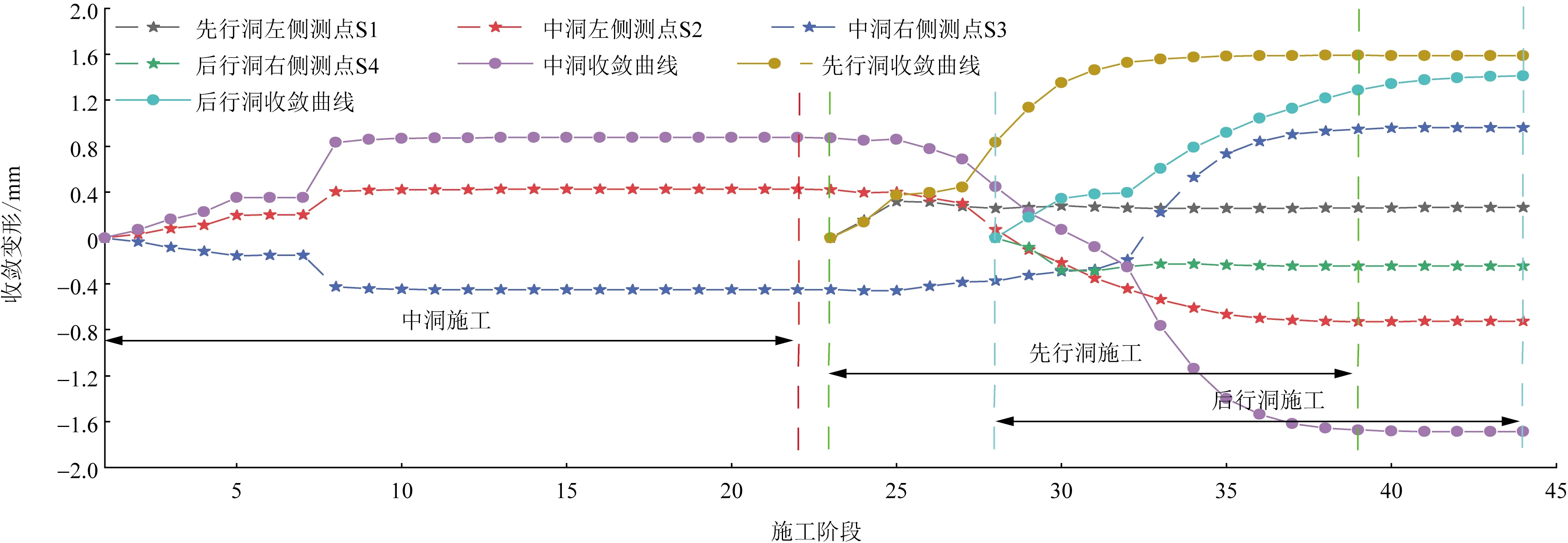
图6 洞周收敛变形曲线Fig.6 Convergent deformation curve of tunnel

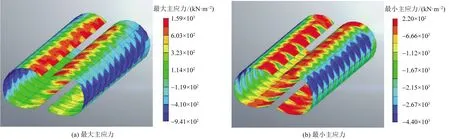
图7 初支结构主应力分布云图Fig.7 Cloud diagram of principal stress distribution in initially supported structure

图8 钢支撑主应力分布云图Fig.8 Cloud diagram of principal stress distribution in steel support

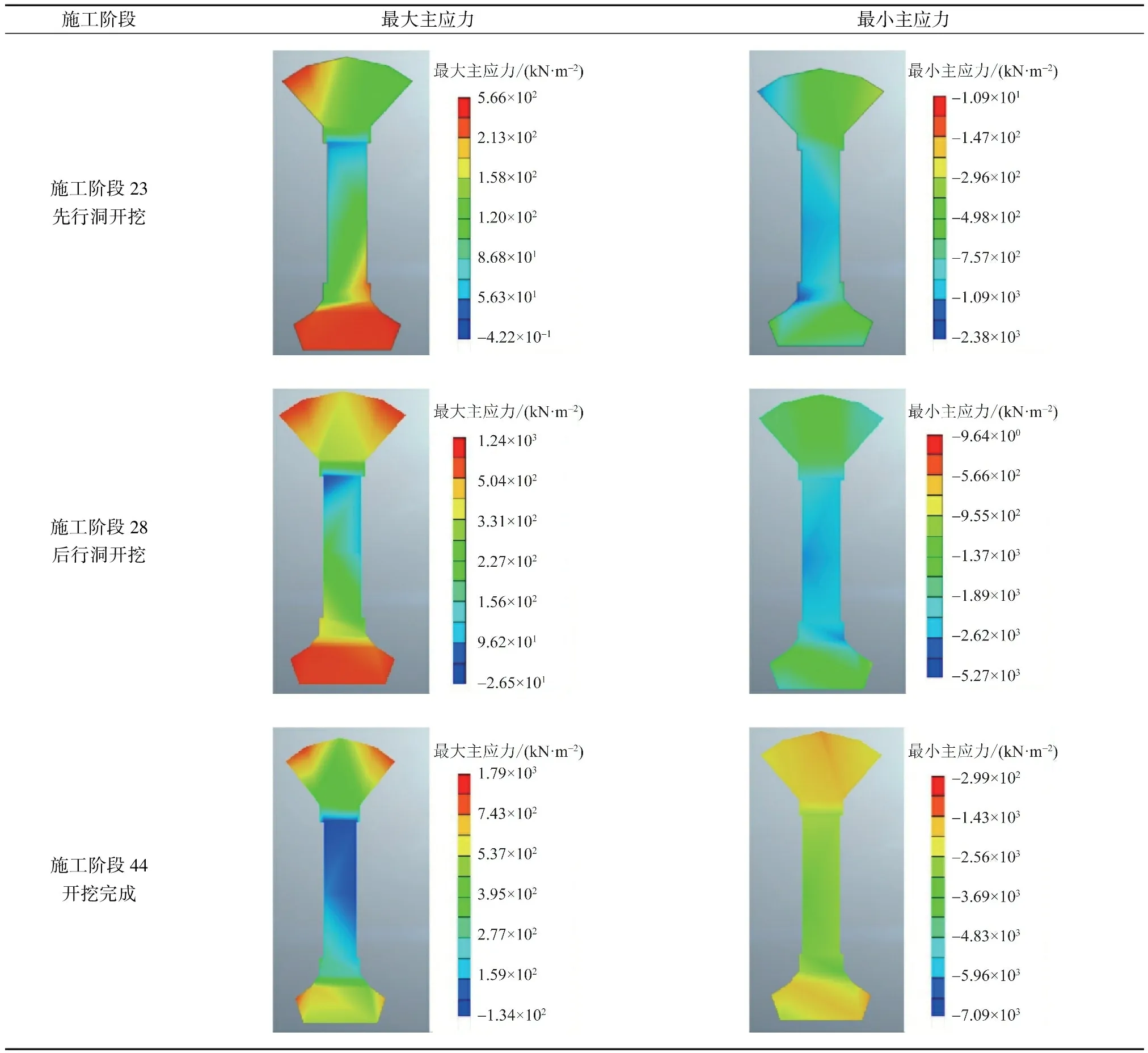
表2 中隔墙应力分布Table 2 Stress distribution of the partition wall

4 地表沉降及现场监测

为研究中洞法隧道施工对地面所产生的影响，选取30 m隧道断面，在模型表面布置监测线L1(图9)，获取开挖过程地表沉降变形曲线如图10所示。

侧洞断面大于中洞导致其开挖引起较大沉降，中洞开挖至监测断面时地表最大沉降量为1.61 mm，沉降曲线呈正态分布，隧道中轴线处为最大沉降部位。先行洞开挖导致沉降曲线向左发生偏移，当先行洞开挖至监测断面时，先行洞轴线处沉降值最大为3.38 mm。后行洞开挖逐渐消除该偏压现象，使最大沉降部位再次向隧道中轴线处转移，后行洞开挖至监测断面时地表最大沉降值为6.50 mm，为验证模拟结果的有效性，需在现场布置测点，利用水平仪、水准仪、测杆等工具获取施工期间地表实际沉降变形数据。沿隧道走向每15 m布置一个监测断面，断面上测点布设以隧道轴线为中心，测点间距逐渐增大(图11)，若实际变形影响范围超过“地面测点布置断面图”图示范围，向外按5 m间距布设测点。根据现场施工进度获取了中洞开挖至监测断面的实际地表沉降曲线(图10)，由于实际地层并非规则层状分布且为各向异性，加之现场施工环境复杂，实测地表沉降值略大于模拟值，但模拟结果所获得的地表沉降规律与实测结果一致，因此可以通过模拟手段指导施工。

图9 地表沉降监测线位置示意图Fig.9 Schematic diagram of surface subsidence monitoring line position

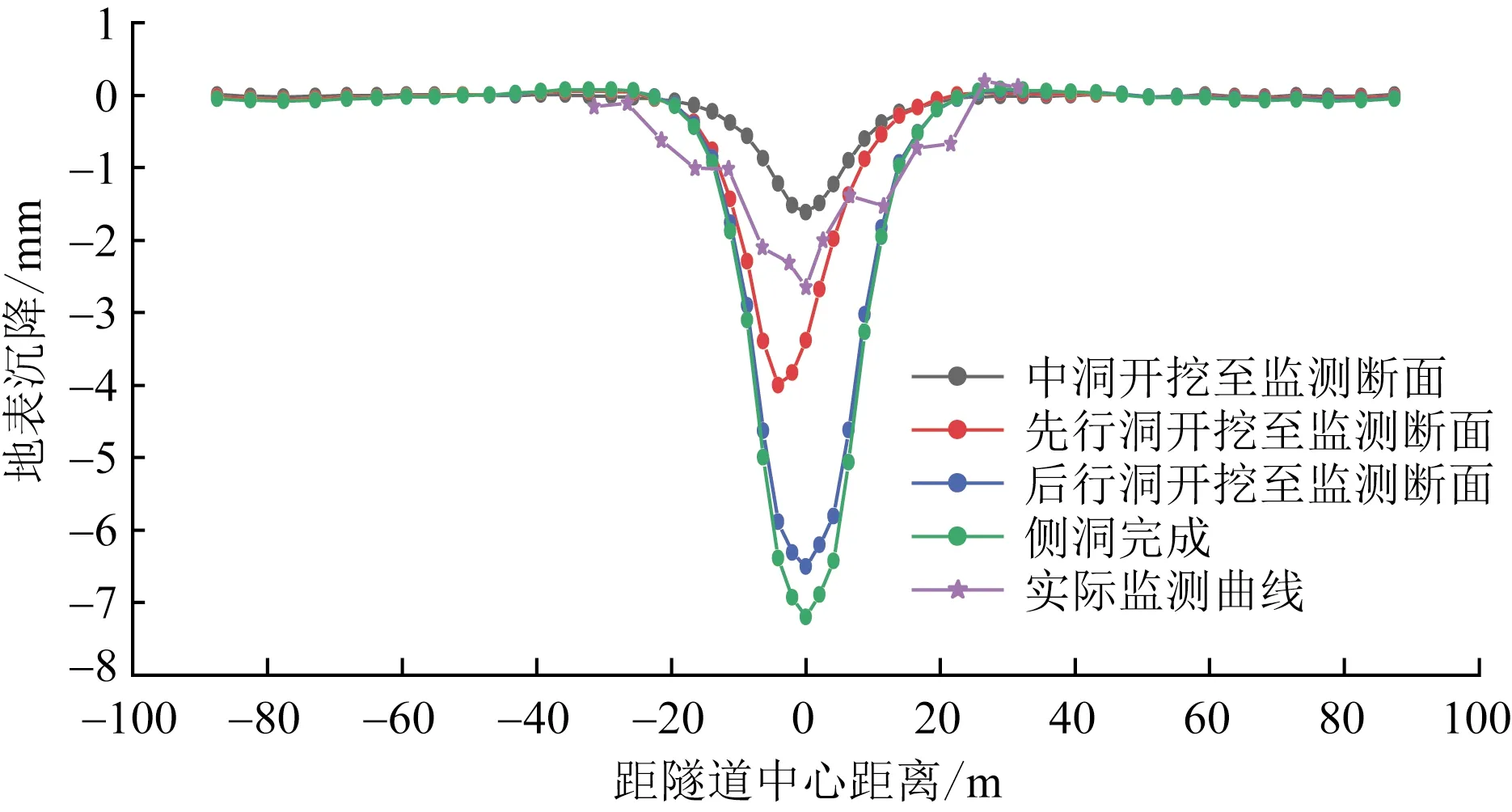
图10 地表沉降曲线Fig.10 Surface settlement curve

5 施工参数优化

工程质量、工期要求、对周边环境影响等因素均是地铁施工所必须考虑的因素，快速高效的施工既能保证全线按期开通又能带来巨大的经济效益。对于采用台阶法施工的连拱隧道，台阶错距、侧洞拉开距离等变量均会对上述因素产生影响[11]，为此研究不同施工参数下隧道工程的稳定性显得尤为重要。以中洞上下台阶错距、侧洞相邻台阶错距以及左右侧洞拉开距离为变量(表3)，采用控制变量法获取各监测指标的变化规律。

选取各监测指标的最大值进行比较来分析不同施工方案下连拱隧道的稳定性(表4)，随中洞台阶长度的拉大拱顶沉降、底部变形、洞周收敛等隧道变形指标呈递增态势，但由于这些指标的最大值均在侧洞处获得，故其随中洞台阶长度变化量较小，地表沉降值则随中洞台阶长度拉大增长明显。隧道变形指标及地表沉降值与侧洞相邻台阶错距呈现正相关关系，且相较于中洞，侧洞台阶错距对这些指标的变化影响更为明显，此外，随侧洞台阶长度增大中隔墙上应力不断增大，而初支结构上的应力则不断减小。拱顶沉降、底部变形及地表沉降随左右侧洞拉开距离的增大而不断减小，两侧洞同步开挖(即VAR3=0)，较大临空面的产生导致应力释放范围增大，故引起变形量增大。与此同时，侧洞同步开挖隧道受施工影响次数减少，洞周收敛变形则相对较小，在该研究中侧洞拉开距离为10 m时受后行洞施工的二次扰动，先行洞洞周收敛值达到最大，为1.59 mm，随侧洞拉开距离的进一步增大，拉开距离对洞周收敛的影响开始减小。中隔墙应力随侧洞拉开距离增大而减小，初支应力随侧洞拉开距离的增大先增大后减小，同步开挖时，两侧临空面的对称出现导致应力快速集中在中隔墙上，因此中隔墙应力较大而初支结构上应力较小，拉开距离为20 m时，左右侧洞相互影响减小，故中隔墙与初支结构上的应力均减小。综上所述，隧道稳定性随中洞上下台阶错距及侧洞相邻台阶错距的增大而减弱，随侧洞拉开距离增大而增强，但各模拟方案均能满足施工要求，因此，实际施工时可根据不同侧重点对施工参数进行优化。

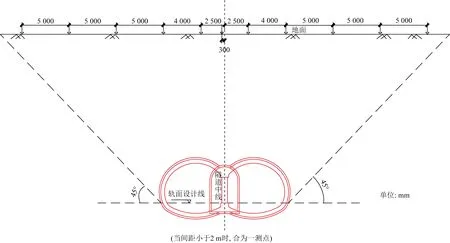
图11 地面测点布置断面图Fig.11 Layout section of ground measurement points

表3 不同施工方案参数设置Table 3 Parameter settings of each construction plan

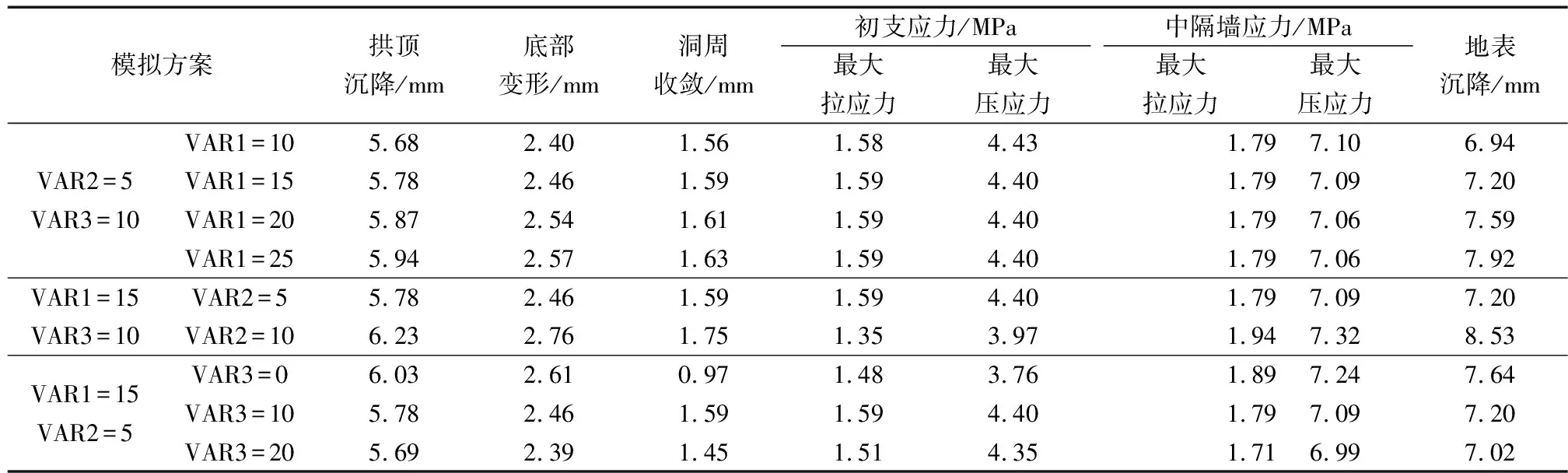
表4 不同施工参数监测指标值Table 4 Monitoring index values of different construction parameters

6 结论

针对中洞法连拱隧道暗挖施工的稳定性问题，综合分析了拱顶沉降、底部变形、洞周收敛、初支结构应力、中隔墙应力及地表沉降的动态响应特征，对不同工艺参数下各监测指标的变化规律进行了总结，得出如下结论。

(1)拱顶沉降最大值及最大沉降速率均在后行洞施工时获得，最大沉降值为5.78 mm；中洞底部变形曲线呈上凸型，而最大隆起值在后行洞60 m处，为2.46 mm；受后行洞开挖二次扰动，先行洞洞周收敛值大于后行洞，分别为1.59 mm和1.41 mm；侧洞靠近中洞上台阶支护结构受拉特征明显，达1.59 MPa，侧洞远离中洞上台阶支护结构受压特征明显，达4.40 MPa；中隔墙中部主要承受压应力，而顶纵梁和底纵梁则同时承受拉应力和压应力。

(2)地表沉降曲线呈正态分布，先行洞开挖会导致沉降最大值向左偏移，但隧道施工完成后沉降最大值位于隧道中心，为7.20 mm，隧道施工影响区域半径约为25 m。实测地表沉降值略大于模拟值，但模拟结果所获得的地表沉降规律与实测结果一致。

(3)隧道稳定性随中洞上下台阶错距及侧洞相邻台阶错距的增大而减弱，随侧洞拉开距离增大而增强，各模拟方案均能满足施工要求，可根据工程侧重点选定施工参数。