新型仿生蜂窝结构的设计与耐撞性能分析

2022-02-18于鹏山刘志芳李世强

高压物理学报 2022年1期

于鹏山，刘志芳，李世强

（太原理工大学机械与运载工程学院应用力学研究所, 山西太原 030024）

蜂窝材料在其平台应力阶段会发生较大的塑性变形，具有良好的吸能特性[1]。蜂窝作为一种常见的多孔材料，具有质量轻、强度高、吸能效率高等良好的力学性能，在航空、航天、汽车等领域具有广阔的应用前景[2-3]。

人们通过理论计算、数值模拟和实验等方法对蜂窝的耐撞性能进行了大量的研究。例如：Xu 等[4]研究了蜂窝结构尺寸与力学性能之间的关系，结果表明，平均平台力与试件尺寸呈线性关系；Mousanezhad等[5]研究了动态冲击时蜂窝的应变硬化对变形模式的扩散效应。近年来，人们越发重视通过新的设计提高结构性能[6-8]。Xiang 等[9]受自然界瓢虫的启发，设计了蜂窝薄壁结构（BHTS），提高了结构的耐撞性能。He 等[10]在荷叶脉的基础上提出了一种叶脉支蜂窝结构，提高了结构的吸能能力。Yang 等[11]设计了具有马蹄形特征的仿生蜂窝，相比传统蜂窝，马蹄形蜂窝具有更高的吸能能力和压缩力效率。He 等[12]受自然界蜘蛛网结构启发，设计了一种具有同轴特征的六边形蜂窝结构，结果表明，仿生蜂窝比普通蜂窝具有更好的耐撞性能。Yang 等[13]设计了一种新的圆蜂窝结构，与常规圆蜂窝相比，新型蜂窝的吸能性能提高了近一倍。Zhang 等[14]为了追求更高的吸能能力和耐撞性，提出了一种新型四弧多蜂窝结构，将层次微结构引入传统的蜂窝中，以改善其力学性能。Zhang 等[15]研究了仿生自相似规则分层蜂窝在面外冲击载荷下的耐撞性。Yin 等[16]研究了具有六边形、三角形等仿生分层蜂窝的面内冲击行为，其中三角形拓扑结构的分层蜂窝具有最佳的耐撞性。Qiao 等[17]提出了一种等边三角形二阶分层蜂窝结构，与正六边形和三角形蜂窝相比，其压缩强度得到了改善。

综上所述，基于仿生学基本原理设计的蜂窝结构可有效地提高蜂窝材料的耐撞性能。本研究基于仿生学基本原理提出一种新型仿生蜂窝的设计思路。受毛竹竹壁的微观结构启发，设计单胞具有双菱形肋骨特征的新型仿竹蜂窝结构；利用有限元软件ABAQUS 对其进行轴向压缩数值模拟，对比仿生蜂窝与传统蜂窝的准静态面外压缩力学性能；采用超折叠单元理论建立新型仿竹蜂窝的动态压缩理论模型，评估仿竹蜂窝的变形模式，以期为仿生蜂窝的理论研究与结构设计提供参考。

1 结构设计

观察毛竹壁结构发现，维管束横截面呈近菱形，且管壁从内到外呈变密度分布，管孔径依次减小，如图1 所示。根据这一特征，在传统圆形蜂窝（round-honeycomb，RH）、传统六边形蜂窝（hexagonalhoneycomb，HH）的单胞基础上增加仿竹内管与双菱形变孔径肋骨，得到仿生圆形蜂窝（bionic-roundhoneycomb，BRH）、仿生六边形蜂窝（bionic-hexagonal-honeycomb，BHH）。仿生蜂窝的几何尺寸如表1所示（传统蜂窝作为对比，其尺寸也列于表中），其中D为BRH 单胞的外径和BHH 单胞的内切圆直径，d为BRH 与BHH 的内管直径，a、b为双菱形肋骨的边长， α为双菱形肋骨夹角。仿生蜂窝的内管、外管和肋骨采用相同的厚度t，4 种蜂窝的高度h均为 20 mm。

图1 仿生蜂窝结构设计Fig. 1 Structural design of bionic honeycombs

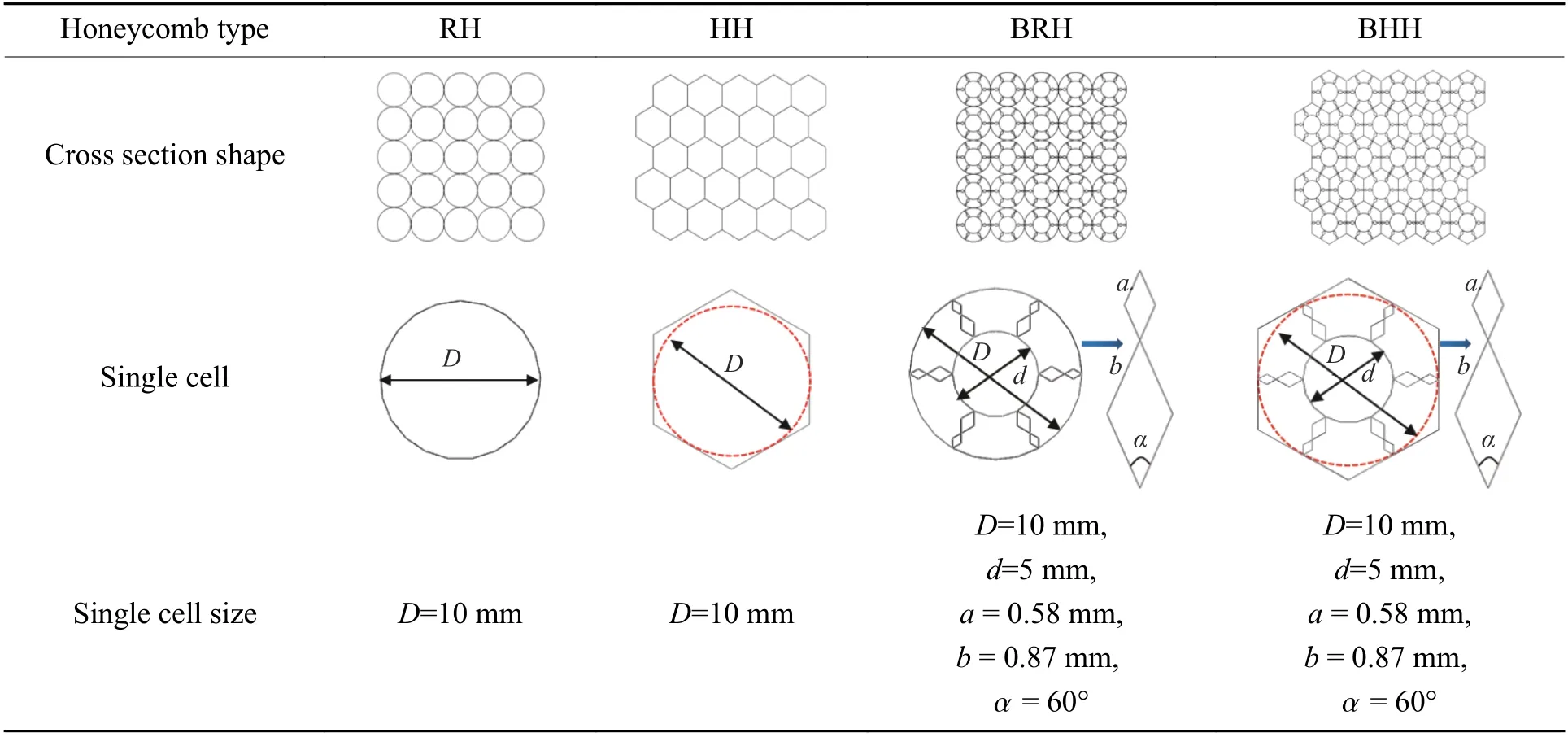
表1 传统蜂窝与仿生蜂窝的结构尺寸Table 1 Structure sizes of traditional honeycombs and bionic honeycombs

2 有限元模型

利用有限元软件ABAQUS 进行数值模拟。蜂窝材料选择铝合金AA3003 H18[18]，初始屈服强度115.8 MPa，极限强度154.5 MPa，弹性模量69 GPa，泊松比0.33，密度2.7 g/cm3。蜂窝薄壁结构的有限元模型采用四边形壳单元构建，以模拟结构的大变形，单元厚度方向采用5 点积分，面内采用单点积分。如图2 所示，有限元模型置于上、下刚性平板之间，下端刚性平板固定全部自由度，上端刚性平板以v=1 m/s 的速度匀速向下压缩蜂窝。上、下刚性平板与蜂窝模型之间的接触和模型各部分之间的接触均定义为通用接触（general contact），接触面切向罚接触摩擦系数取0.2，法向硬接触，允许接触后分离。网格较大会影响模拟结果的准确性，网格较小会消耗大量计算资源，因此有必要对有限元模型进行网格敏感性验证。采用六边形蜂窝（六边形内切圆直径D= 10 mm，六边形蜂窝结构单胞边长L= 5.77 mm，蜂窝高度h= 20 mm，壁厚t= 0.075 mm）的有限元模型验证网格敏感性，验证结果如图3 所示。随着网格尺寸的减小，载荷-位移曲线逐渐趋于稳定。综合考虑计算效率与计算精度，蜂窝模型适宜的网格尺寸为0.25 mm。继而，对传统六边形蜂窝进行面外压缩数值模拟。图4 显示了模拟结果与实验结果[12]，对比可知，数值模拟与实验得到的结构在压缩过程中的载荷-位移曲线吻合较好。因此，建立的有限元模型有效，可用于研究不同类型仿生蜂窝的面外压缩力学性能。

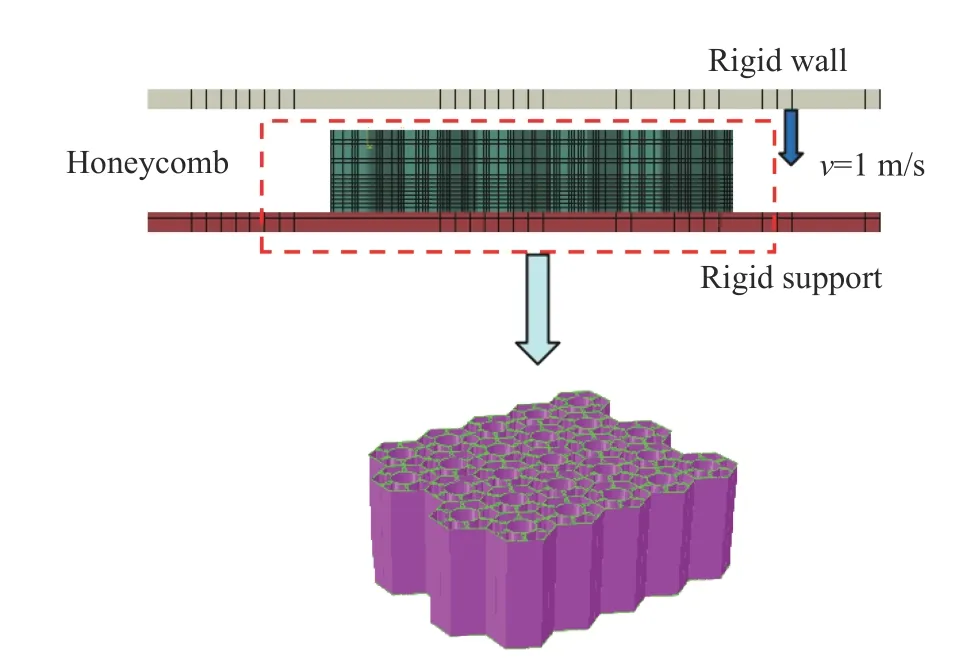
图2 仿生蜂窝有限元模型Fig. 2 Finite element model of bionic honeycomb

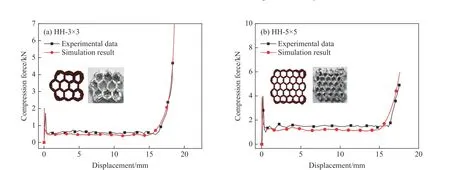
图4 数值模拟与实验[12]结果对比Fig. 4 Comparison of numerical simulation and experimental results[12]

3 面外压缩耐撞性指标

4 不同类型蜂窝的准静态压缩

为了探究不同蜂窝的耐撞性能，改变蜂窝壁厚t以固定仿生蜂窝与传统蜂窝的质量（M= 7.30 g），对4 种蜂窝进行面外准静态压缩数值模拟，模拟结果如图5 所示。

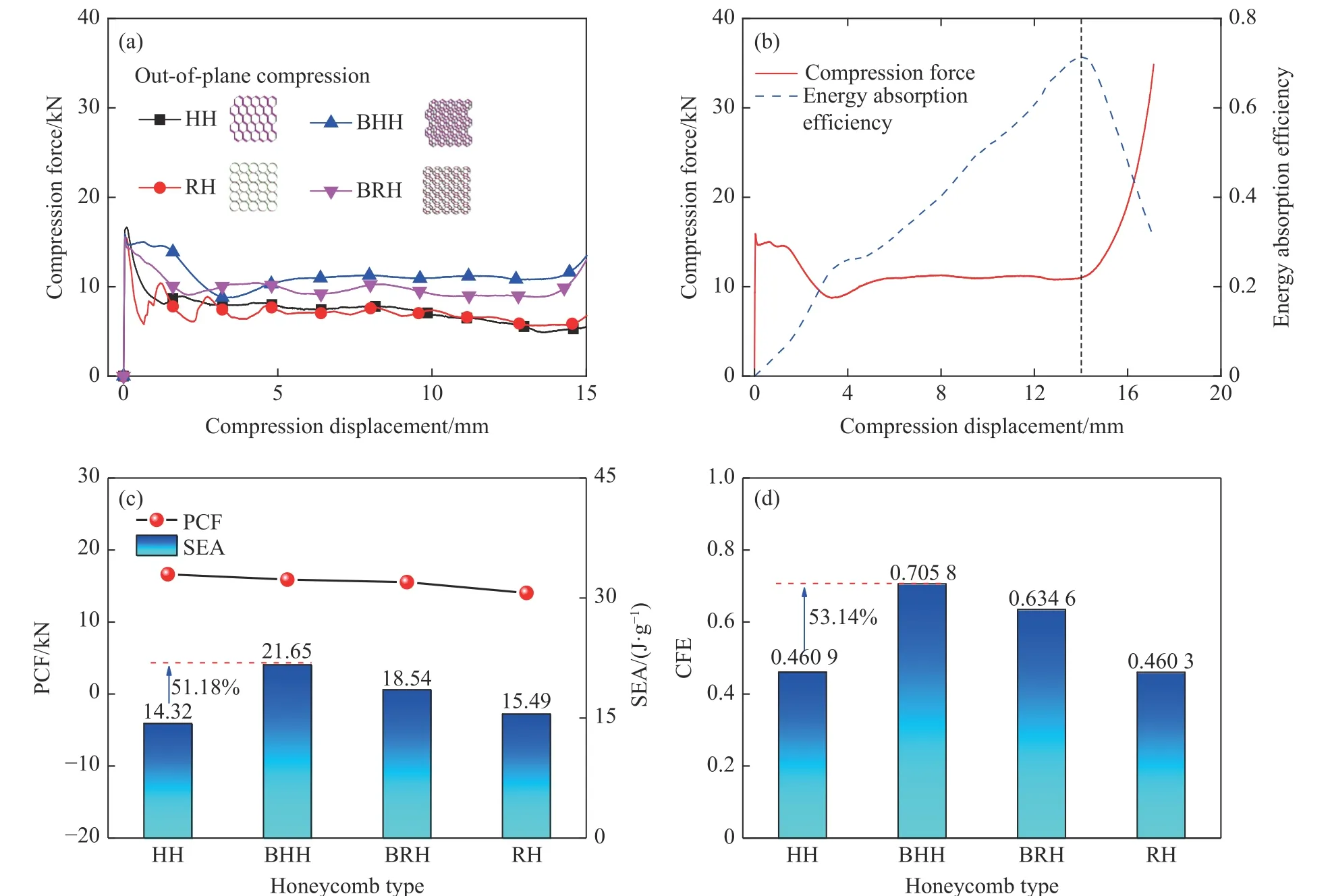
图5 不同类型蜂窝的耐撞性比较：(a) 载荷-位移曲线，(b) BHH 的载荷-位移曲线，(c) PCF 和SEA，(d) CFEFig. 5 Crashworthiness comparison of different honeycombs: (a) load-displacement curve,(b) load-displacement curve of BHH, (c) PCF and SEA, (d) CFE

由图5(a)可知，相比其他3 种蜂窝，BHH 具有更高的平台区域，结构力学性能更优。由图5(b)可知，BHH 具有多胞结构典型的三阶段特征：弹性阶段、平台阶段和密实化阶段。由图5(c)和图5(d)可知，同等质量下，BHH 的SEA 为21.65 J/g，比HH 的SEA 提高了51.18%，CFE 值提高了53.14%。4 种蜂窝中RH 的比吸能最低。由于BHH 结构中存在的双菱形肋骨为其压缩过程中的塑性变形提供了更多支撑，因而具有更好的耐撞特性。值得注意的是，BHH 的CFE 也是4 种蜂窝中最高的，为0.705 8，见图5(d)。综合以上结果可知，具有仿竹微观结构的仿生六边形蜂窝具有较好的耐撞性能。

5 仿生蜂窝理论分析

基于简化的超折叠单元理论（simplified super folding element theory）[20]，建立理论分析模型，预测其耐撞性和吸能特性。假设在结构的渐进折叠变形中，每一次折叠的折叠波长是相同的。根据虚功原理，完全压缩至褶皱形成过程的外功被弯曲变形和膜的塑性变形所耗散，表达式为

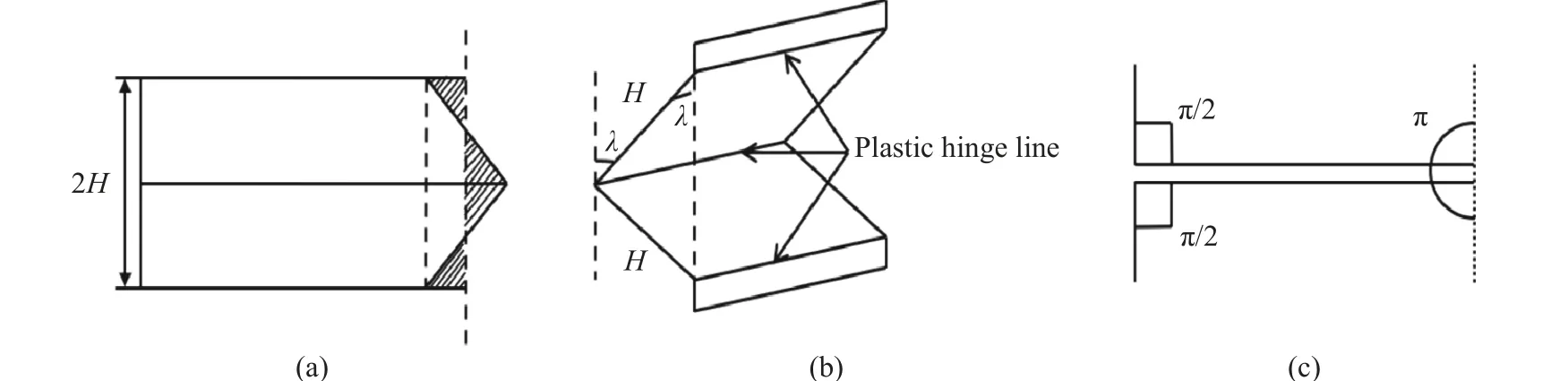
图6 简化超折叠单元模式[20]：(a)拉伸单元，(b)弯曲塑性铰线，(c)基本折叠单元凸缘完全压缩Fig. 6 Scheme of simplified super folding element: (a) extensional element, (b) bending hinge lines,(c) full compression of flange (basic folding element)

5.1 弯曲变形耗散能量

5.2 薄膜变形耗散能量

图7 仿生蜂窝单胞变形模式：(a) BHH 单胞，(b) BRH 单胞Fig. 7 Bionic honeycomb single cell deformation mode: (a) BHH single cell, (b) BRH single cell

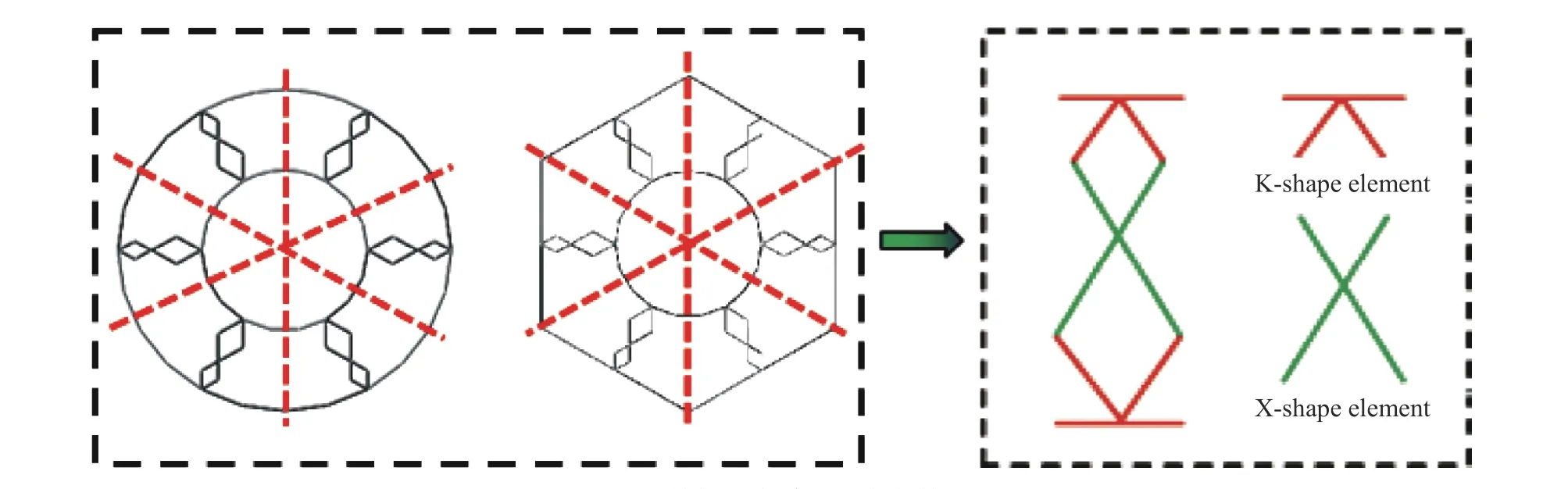
图8 结构基本单元分布与简化Fig. 8 Distribution and simplification of basic constitutive elements

图9 显示了X 型单元与K 型单元的具体结构。

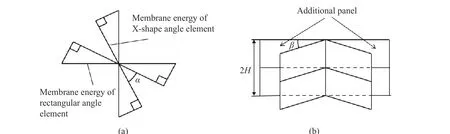
图9 基本角单元：(a) X 型单元，(b) K 型单元Fig. 9 Basic angle element: (a) X-shape element, (b) K-shape element

6 结果与讨论

6.1 理论预测与数值模拟对比

利用式(19)和式(20)计算BHH 和BRH 的动态平均压缩力pmd，并与数值模拟结果进行对比。其中，数值模拟中的平均压缩力是利用面外压缩仿生蜂窝的载荷-位移曲线（图10），结合式(1)、式(2)和式(3) 得到。表2 给出了仿生蜂窝的理论预测与数值模拟结果，可见二者吻合较好，相对误差均在10%以内。这表明基于简化超折叠理论建立的模型可以有效预测新型仿生蜂窝的能量吸收性能，可为仿生蜂窝的设计提供理论指导。

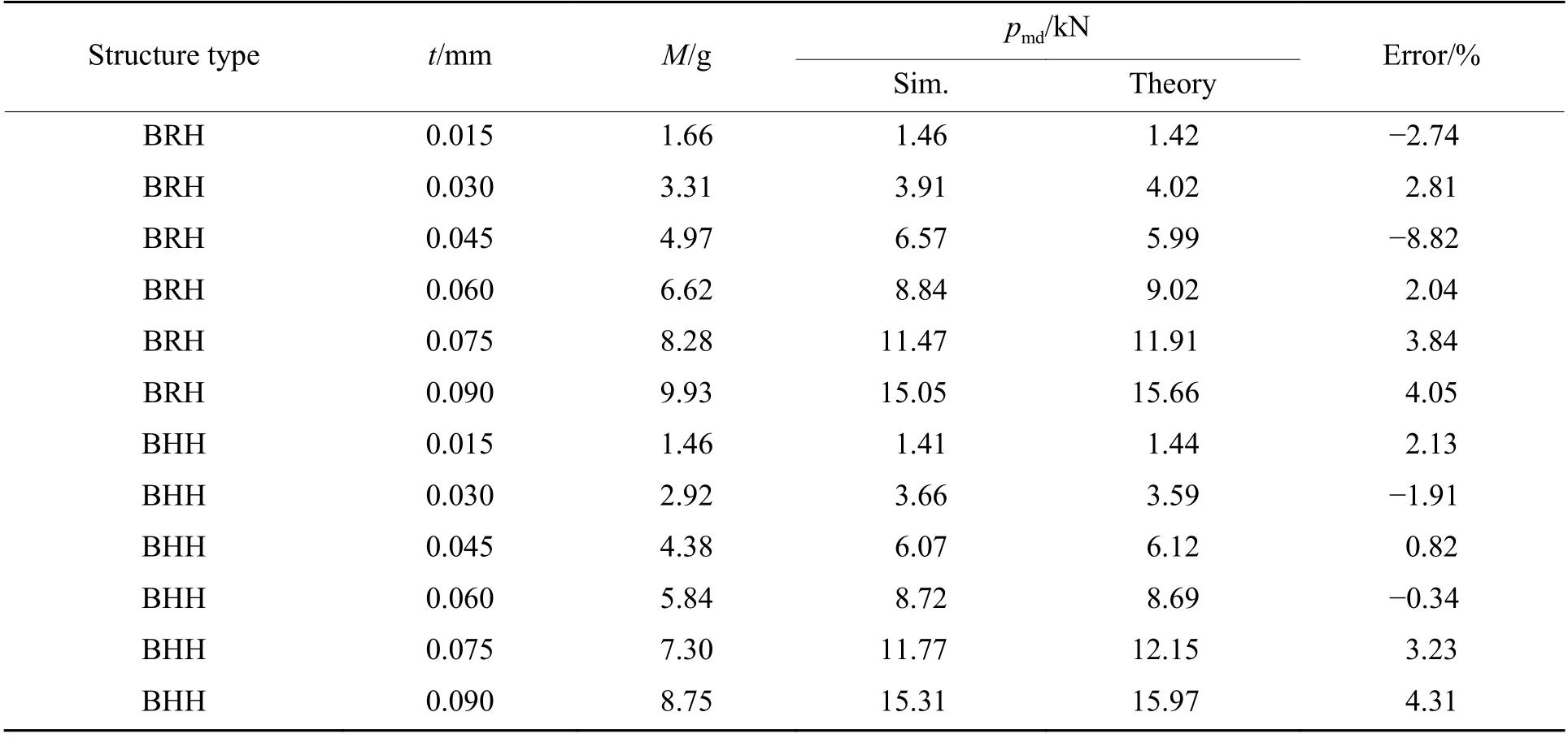
表2 数值模拟与理论预测结果对比Table 2 Comparison of numerical simulation and theory

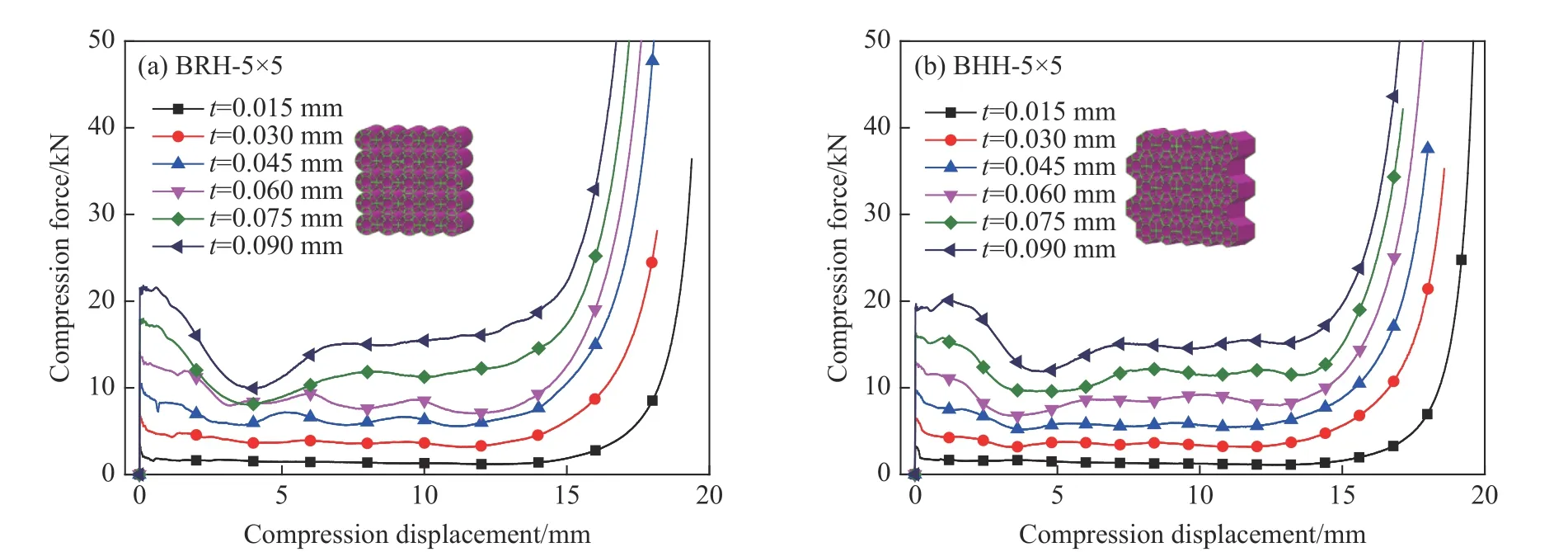
图10 仿生蜂窝的载荷-位移曲线：(a) BRH，(b) BHHFig. 10 Load-displacement curves of bionic honeycombs: (a) BRH, (b) BHH

6.2 壁厚的影响

对仿生蜂窝BHH 和BRH 分别选取6 种壁厚（0.015、0.030、0.045、0.060、0.075 和0.090 mm），分析壁厚对动态压缩性能的影响，如图11 所示。

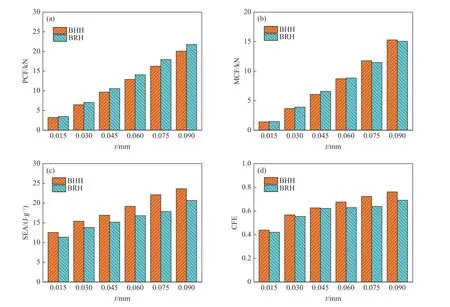
图11 不同壁厚下两种仿生蜂窝的耐撞参数对比Fig. 11 Crashworthiness comparison of two bionic honeycombs at different thicknesses of membrane

图11(a)和图11(b)显示，两种蜂窝的平均压缩力和初始峰值力均随着胞壁厚度的增加而增大，即选择较厚的胞壁可以提高仿生蜂窝在轴向压缩作用下的抗屈曲能力和抗冲击能力。由图11(c)可知，壁厚对比吸能有显著影响，且BHH 的比吸能均高于BRH。仿生蜂窝BHH 在壁厚t= 0.090 mm 时的比吸能为23.65 J/g，比t= 0.060 mm 时的比吸能（15.39 J/g）提高了53.67%，表明蜂窝壁较厚的BHH 在压缩过程中可吸收更多的冲击能量。图11(d)显示，两种仿生蜂窝的压缩力效率均随蜂窝壁厚度的增加而增大。但是当初始峰值力过高时，可能对蜂窝结构所保护物体造成严重的损伤，因而需将初始峰值力最小化，以降至不破坏被蜂窝所保护物体的结构的安全水平。由此可见，适当的胞壁厚度对于设计高效的能量吸收器是至关重要的。综合来看，BHH 的耐撞性参数比BRH 好。

6.3 肋骨夹角的影响

对两种仿生蜂窝BHH 及BRH 取不同的双菱形肋骨夹角α，分析肋骨夹角对耐撞性能的影响。如图12(a)所示，肋骨夹角对初始峰值力有显著影响，两种仿生蜂窝的初始峰值力随着肋骨夹角的增大有逐渐增大的趋势。初始峰值力过高会对被蜂窝结构保护的物体造成损伤。由图12(a)和图12(b)可知，MCF 受肋骨夹角的影响与PCF 类似。值得注意的是，相同肋骨夹角时BHH 的比吸能均高于BRH，见图12(c)，比如 α=75°时，BHH 的比吸能为22.14 J/g，比BRH 的比吸能（19.65 J/g）提高了12.67%。此外，对于同种仿生蜂窝，肋骨夹角对比吸能有显著影响，例如：BHH 在肋骨夹角α=75°时的比吸能为22.14 J/g，比α=30°时的比吸能（17.77 J/g）提高了24.59%。图12(d)显示，两种仿生蜂窝的压缩力效率均随肋骨夹角的增大有逐渐增加的趋势。图13 给出了BHH 和BRH 的变形模式。由图13(a)和图13(b)可知，两种仿生蜂窝在压缩时均出现渐进折叠模式，该模式可以保证结构在压缩时压缩力的稳定，有利于提高结构的能量吸收效率。由图13(c)和图13(d)可知，BHH 和BRH 内部双菱形肋骨的引入使结构具有更多支撑，使得两种仿生蜂窝都具有较好的吸能特性。综合考虑耐撞性参数，适当的肋骨夹角对于设计高效的能量吸收器至关重要。

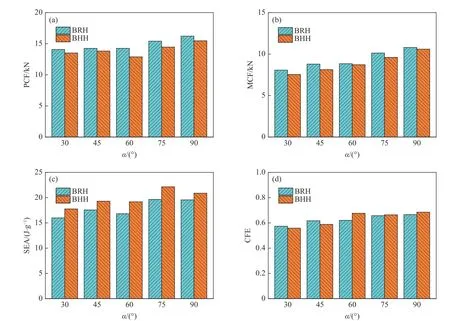
图12 不同肋骨夹角下两种仿生蜂窝的耐撞参数对比：(a) PCF，(b) MCF，(c) SEA，(d) CFEFig. 12 Crashworthiness comparison of two bionic honeycombs at different rib angles: (a) PCF, (b) MCF, (c) SEA, (d) CFE

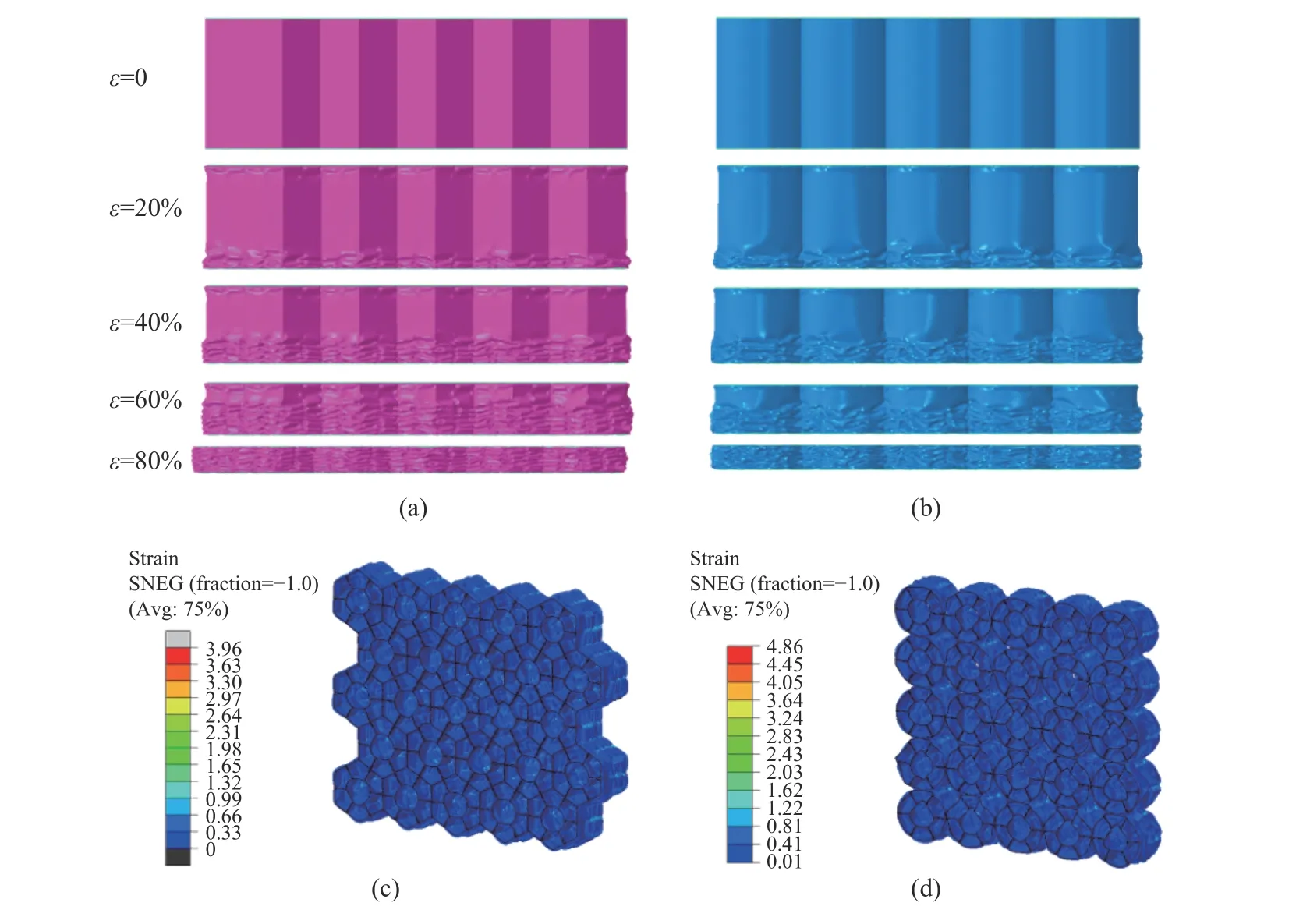
图13 仿生蜂窝的变形模式与应变云图：(a) BHH 的变形模式，(b) BRH 的变形模式，(c) BHH 的等效塑性应变，(d) BRH 的等效塑性应变Fig. 13 Deformation modes and equivalent plastic strain of the bionic honeycombs: (a) deformation mode of BHH,(b) deformation mode of BRH, (c) equivalent plastic strain of BHH, (d) equivalent plastic strain of BRH