冲击加载下金属铝中氦泡演化行为的相场模拟

万 曦，姚松林，裴晓阳

（中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室, 四川 绵阳 621999）

材料在加工和储存过程中不可避免地会产生缺陷。缺陷的存在可能显著影响材料的力学性能，因此相关研究得到持续的关注。放射性环境下，材料可能遭受氦原子或氦离子等粒子的辐照，从而在材料中形成氦泡等缺陷[1-2]。已有研究表明，氦泡的存在会显著影响材料的力学性能[3-6]，包括动力学性能和静力学性能。早期的研究集中在准静态研究领域，主要关注氦泡导致的氦脆与肿胀现象[3-7]。近年来，强动载荷下氦泡的行为与影响得到越来越多的关注[8-22]。强动载荷下材料的变形是一个超快动力学过程，力学响应一般呈现显著的时间非平衡和空间非均匀等特性，相关研究十分复杂而困难。然而，受测量手段和实验条件的限制，无法实时得到冲击过程中材料内部的演化过程[23-25]。当前，人们主要通过测量强动载荷下材料的界面粒子速度获得高时间分辨的动态变形信息，再结合样品回收表征以及理论建模反推材料内部的变形过程[26-29]。

微介观尺度下，人们主要通过表征回收样品[14-15]或者原子模拟[18-20]获得氦泡的演化规律及其对局域塑性变形的影响特征。Glam 等[17]通过表征回收样品，发现冲击加载前后氦泡出现明显的聚集长大特征，这对深入认识损伤演化早期底层变形机理具有十分重要的意义。Shao 等[18]通过原子模拟对整个层裂过程中损伤形态的演化进行了研究，指出动态拉伸过程中大孔洞的形成源于小孔洞的汇合，而初始孔洞与氦泡的存在抑制了孔洞的长大。此外，Kubota 等[12]通过在模型中预设不同类型的初始缺陷，研究了不同类型的初始微缺陷及不同尺寸的氦泡对材料动态强度的影响；王海燕等[8]则对氦泡局域应力分布导致的位错演化非均匀性进行了研究。

宏观尺度下，人们通过测量速度波剖面，获取了含孔洞材料的状态方程、屈服强度以及拉伸强度，通过建立基于均匀化假设的唯象模型，对实验现象进行了解释。例如：Reisman 等[10]首先采用准等熵实验获得了孔隙度对辐照不锈钢力学响应的影响规律，随后通过建立含孔洞坍缩的演化方程，再现了因孔洞坍缩导致波剖面塑性前沿斜率显著降低的关键特征。Raicher 等[13]建立了含氦泡铝的状态方程，并检验了氦泡的存在对材料冲击加载响应的影响。Glam 等[17]采用冲击加载手段对反应堆辐照掺硼铝样品的层裂强度进行了系列研究，结果表明，不同环境温度下氦泡对层裂强度的贡献呈现相反的趋势，室温下氦泡的存在导致层裂强度增大，而高温下则导致层裂强度显著降低。他们采用一个含氦泡内压的唯象模型，再现了室温下氦泡导致层裂强度增大的实验现象，却没有明确指出导致该现象的原因。对于高温下氦泡导致层裂强度减小的实验现象，Glam 等则定性地指出，可能是由于氦泡的存在降低了塑性流动，同时有助于孔洞增长。

总的来说，当前对氦泡如何影响材料动力学行为的研究，无论是实验还是理论模拟都相对较少。如何利用有限的实验数据获取更丰富的动态变形信息，对数值模拟工作提出了更高的要求。宏观模拟完全忽略了微结构演化行为，对真实物理过程的描述不够合理，且完全忽略了氦泡与位错的相互作用。原子模拟可以有效地描述单个氦泡的演化行为及其对局域位错演化的影响，但所能描述的时空尺度有限，且原子模拟结果难以给出氦泡演化行为对位错集体演化行为的影响，进而限制了其为更大尺度力学响应特征提供理论支撑。

就动载下氦泡的演化行为而言，目前还缺少一个可以在更大时空尺度下考虑氦泡微结构效应，并可有效描述氦泡与位错演化相互影响的模拟技术。在前期的工作中，我们已证实相场（phase field）方法可以有效描述冲击下新相的生长过程，并能够与宏观力学响应有效关联起来。类比新相生长过程，氦泡的生长过程同样有望用相场方法描述，而晶体塑性理论可以在连续尺度描述塑性流动行为。为此，本研究将相场方法引入冲击加载下氦泡的动态演化行为分析，通过与晶体塑性理论耦合，对冲击加卸载过程中氦泡的演化行为及其对局域塑性变形的影响进行探讨，以获得规律性认识。相关研究可为解读宏观强度行为提供理论参考。

1 理论模型

在模拟材料的动态力学响应时，一般选用流体弹塑性模型描述[30]。基于流体弹塑性假设，可将变形拆分为球量响应和偏量响应，分别采用状态方程和本构模型予以描述。本研究将在流体弹塑性理论框架下处理含氦泡铝材料的力学响应。

分别建立不同的模型描述基体铝材料和氦泡的力学响应，采用相场模型描述氦泡的演化，采用晶体塑性模型描述基体铝材料的弹塑性响应。采用晶体塑性模型描述基体铝材料的弹塑性响应的原因在于，大量的研究已经证实晶体塑性模型可以较合理地描述冲击加载下材料的黏塑性响应，从而更加准确地预测氦泡/基体铝材料界面处的应力分布，进而更加合理地描述氦泡生长行为。而选择相场模型描述氦泡的演化行为则主要是由于相场方法具有强大的界面处理能力。下面将分别介绍相场模型和晶体塑性模型。

1.1 流体弹塑性分解

1.2 晶体塑性模型

晶体材料的塑性变形主要由位错滑移和孪晶变形引起，而位错作为塑性变形的基本单元在这两种机制中都起着重要作用[34]。采用Orowan 方程可将宏观层面的塑性应变率与微观层面的位错运动以及位错生成关联起来，其表达式为

采用Austin 等[38-39]提出的基于位错亚结构演化的本构模型描述位错密度演化，根据位错在塑性变形过程中的作用将位错区分为可动位错和不可动位错。可动位错负责塑性滑移，不可动位错负责控制材料的屈服应力，则有

1.3 基于相场方法的氦泡演化模型

相场模型是目前模拟材料微结构演化的重要的理论与计算工具。相场方法的优势在于可以反映界面演化的动力学效应。基于扩散界面的思想可以有效避免求解具有运动边界条件的微分方程组这一复杂的数学问题。相场模型借助序参量（场变量）将尖锐界面扩散为具有一定厚度的界面，界面的演化通过序参量的演化来实现[40-44]。

在求得序参量之后，就可以进一步求解压力与温度的演化。这里将压力和温度随时间的变化率表示为比容和序参量随时间变化率的函数，即

在实际计算过程中，考虑到氦泡内压与物质密度均远低于外加载荷，因此忽略氦泡物质密度以及内压对计算结果的影响，即假设氦泡的密度和内压均为零。在处理氦泡覆盖的区域或氦泡/基体界面处相关力学参量时，物质密度、应力与内能均视为两种材料的加权平均，即

2 计算模型

2.1 计算模型介绍

上述物理模型通过二次开发的二维有限元程序实现。其中，相场模型和晶体塑性模型已经在前期工作中应用于冲击相变和动态塑性变形行为研究，模型的合理性及有效性得到验证[28-29,44]。

对含氦泡铝材料进行模拟研究，二维几何模型如图1 所示，模型宽1 μm，长5 μm。模型包括飞片和样品，模拟从冲击瞬间开始；模型下半部分为飞片，存在一个初始速度，即冲击速度；上半部分为铝样品，初始速度为零。截取横向足够长铝板中宽1 μm 的一段，左右边界的横向位移设置为零，上边界为自由界面。模型网格大小为10 nm，横向节点数为101，纵向节点数为501，总节点数为50 601。在模型中固定或随机选取节点，设置初始序参量为1，即初始氦泡位置和大小，其他节点对应基体铝材料，初始序参量设置为零。

2.2 模型参数

应用相场方法描述氦泡的演化，选用关键参数—动力学系数来控制界面演化速率，即氦泡生长速率。在有限元框架下，较大的变形将导致计算难以推进，为此选择较小的动力学系数。不同的动力学系数描述的氦泡生长速率存在差异，但不影响对氦泡与位错集体演化行为相互作用的规律性判断。通过设置不同的飞片冲击速度和动力学系数，发现氦泡增长速率与冲击速度、动力学系数正相关，需要通过设置冲击速度和动力学系数避免氦泡生长过快。经过对比，选取冲击速度为100 m/s、动力学系数L=500进行模拟。晶体塑性模型相关参数在前期工作中有详细讨论。

计算中所使用的材料参数和模型参数如表1、表2、表3 和表4 所示。表1 列出了金属铝的状态方程与声子拖曳系数等参数，B0为室温声子拖曳系数，B′T为声子拖曳系数关于温度的导数。表2 列出了金属铝的弹性常数（c11、c12、c44）及其关于温度的导数（dc11/dT、dc12/dT、dc44/dT）。表3 列出了晶体塑性模型参数，αHN为参考成核速率，αMult为无量纲模型参数，αanni为表征湮灭速度的无量纲参数，vI为俘获过程中的特征速率，ρinitial为初始位错密度，模型参数的确定参见文献[45]。表4 列出了相场模型参数。

表1 状态方程参数与声子拖曳系数Table 1 Parameters of equation of states and phonon drag coefficients

表2 弹性常数及其关于温度的导数Table 2 Elastic constants and temperature derivatives of the elastic constants

表3 晶体塑性模型参数Table 3 Parameters of the crystal plasticity model

表4 相场模型参数Table 4 Parameters of the phase field model

3 计算结果与分析

本研究模拟的实验构型为飞片撞击样品，飞片与样品相互作用后，在界面处分别向样品和飞片中发射冲击波，冲击波与飞片后界面和样品自由面作用后，反射稀疏波。两束稀疏波在样品中相遇，产生拉应力，导致局域孔洞或氦泡生长和聚集，最终形成层裂。图2 为应力波的传播示意图。

图2 应力波传播示意图Fig. 2 Schematic diagram of evolution of stress wave

应用上述模型，对冲击下金属铝中的氦泡演化行为及其对局域位错集体演化行为的影响进行了数值模拟研究。主要研究内容包括3 个部分：氦泡的结构非均匀性、冲击下单个氦泡的生长行为以及两个或多个氦泡的聚集长大行为。

3.1 氦泡的结构非均匀性

首先模拟分析了冲击压缩过程中单个氦泡与冲击波的相互作用。模拟结果表明，冲击波到达后，氦泡的结构非均匀性导致局域应力集中和塑性变形集中。从分切应力云图可以看出，分切应力最大值集中在4 个对角线方向，对应剪应力最大方向，如图3 所示。

图3 冲击波到达后（0.1 ns 时刻）氦泡附近的局域化效应Fig. 3 Localization effect near the helium bubble at the arrival of the shock wave (0.1 ns)

从计算结果中提取了冲击压缩过程中位错密度的演化历史，如图4 和图5 所示。计算结果表明，可动位错密度主要集中在撞击面附近以及氦泡的4 个对角线方向，最大位错密度约为1015m-2。特别地，氦泡附近4 个对角线方向对应剪应力最大值方向。随着应力波在样品中反复传播，氦泡对角线方向高位错密度区域逐渐扩展，同时氦泡周围的位错密度不断累积，在二维空间内逐渐将对角线方向高位错密度区域连接起来，如图5 所示。

除变形局域化以外，计算结果表明，氦泡的存在还会导致应力波传播发生改变。冲击波与氦泡相互作用会导致沿冲击波传播方向发射稀疏波，沿垂直于冲击波传播方向发射压缩波，体现为氦泡附近纵向区域的压力低于铝基体区域，而横向区域的压力高于铝基体区域，如图3(a)和图3(b)所示。

氦泡与冲击波相互作用引起的应力波传播改变与于继东[40]模拟的相变微结构与冲击波相互作用的结果一致。根据Yao 等[45]和Gurrutxaga-Lerma 等[46]最新的动态塑性变形研究结果可知，沿纵向发射的稀疏波实则为冲击波阵面上塑性松弛所发射的稀疏波。由于波后区域是超声速的，Gurrutxaga-Lerma 等在研究“弹性前驱衰减”现象时指出，该稀疏波会追赶上冲击波前，导致“弹性前驱衰减”现象出现。基于该认识，可以预期，氦泡与冲击波相互作用发射的稀疏波最终也会追赶上冲击波前，并导致弹性前驱进一步衰减。该研究结果能够解释Glam 等[17]在实验中发现的含氦泡掺硼铝的动态屈服应力略低于不含氦泡掺硼铝，即含氦泡材料的动态屈服应力略小于不含氦泡材料的动态屈服应力。

3.2 冲击下单个氦泡的生长行为

Glam 等[17]对含氦泡掺硼铝材料进行了冲击实验，结果显示冲击后氦泡出现长大特征。在本研究的模拟过程中，如果不对氦泡在应力波传播过程中的演化行为做任何限制，氦泡会在冲击压缩波的作用下出现变形，模拟结果趋于不可控，与前人的实验结论背离，因此基于前人实验得出的氦泡演化物理图像，限定氦泡仅在拉伸应力的作用下长大，在压应力的作用下不发生演化。从计算结果中提取氦泡尺寸随时间的变化关系，并对时间求微分，从而获得了氦泡长大速率随时间的变化关系。在统计氦泡尺寸时，将序参量大于0.5 的区域确定为氦泡的直径，即半高全宽法。

计算结果表明，卸载波到达前，氦泡直径几乎不发生变化，如图6 所示，0.5 ns 时序参量分布几乎与开始时设置的序参量分布相同，与真实的物理图像一致。由图7、图8 和图9 可知，氦泡的生长行为在卸载波到达后才较为显著，生长速率（dR/dt）在第1 次与第2 次卸载波到达时最大。随后，氦泡的生长速率迅速衰减，后期氦泡尺寸几乎不发生变化。图9 中纵向剪应力演化历史与氦泡生长速率演化相对应：压缩波到达后，剪应力迅速上升，塑性变形导致剪应力最终被松弛至屈服面，压缩应力作用下氦泡不发生演化；稀疏波到达后，剪应力反向增大，拉伸剪应力作用下氦泡的生长速率迅速增大；随着冲击波在材料中不断传播和反射，剪应力幅值不断下降，氦泡的生长速率不再显著。

图6 不同时刻氦泡序参量的空间分布Fig. 6 Spatial distribution of order parameter at different times

图7 第1 次与第2 次卸载波到达后氦泡的演化行为Fig. 7 Evolution of helium bubbles when the first and second unloading waves arrive

图8 氦泡生长速率随时间的变化关系Fig. 8 Time history of the growth rate of helium bubbles

图9 氦泡附近纵向应力演化历史Fig. 9 Time history of longitudinal shear stress near the helium bubbles

从能量的角度来讲，随着冲击波在样品中不断传播与反射，塑性耗散和氦泡演化共同导致能量耗散，卸载波初次到达氦泡所在区域时所携带的能量最大，为氦泡快速生长提供了条件，氦泡快速生长不断消耗卸载波所携带的能量，使卸载波携带能量急剧降低，进而导致氦泡演化驱动力减小，因此氦泡的生长速率在卸载波到达后达到极大值，随后发生显著衰减。

3.2.1 塑性模型对氦泡演化行为的影响

采用理想弹塑性模型和晶体塑性模型计算的氦泡长大行为存在差异，对比结果如图10 所示。可见，采用晶体塑性本构模型计算的氦泡长大速率更快。

图10 在300 K 环境温度、100 m/s 的加载速度下不同模型模拟的氦泡长大速率Fig. 10 Growth rates of helium bubbles simulated by different constitutive models at 300 K and impact velocity of 100 m/s

晶体塑性模型与理想弹塑性模型的最大差异在于对屈服行为的描述。在理想弹塑性模型中，剪应力松弛至屈服的过程瞬间发生并完成，因此应用该模型计算时剪应力始终处于较低水平。而黏塑性本构模型中，剪应力的松弛是一个弛豫过程：在弹性前驱波作用下，剪应力迅速上升，有限的位错滑移来不及将剪应力迅速松弛下来；塑性冲击波到达后，一方面塑性压缩使剪应力不断增加，而塑性松弛又使剪应力不断减小；随着位错密度的累积，塑性松弛效应主导剪应力演化，剪应力迅速下降，直至达到临界分切应力[23,25]。该过程对应整个冲击前沿，在该过程中剪应力得以更多地参与到驱动氦泡长大。因此，采用黏塑性本构模型计算的氦泡长大速率高于采用理想弹塑性模型的计算结果，从而进一步表明一个准确的塑性本构模型对描述非均匀微结构演化行为和影响的重要性。

3.2.2 温度对氦泡演化行为的影响

采用同样的构型和模型参数，计算了600 K 环境温度下氦泡的演化行为，并与室温下氦泡的演化行为进行了对比，如图11 所示。计算结果表明，氦泡的生长速率随温度的升高而增大。该现象可以归因于声子拖曳机制主导冲击加载下的位错运动。在研究FCC 金属的动态屈服应力热硬化现象时，Yao 等[45]指出，声子拖曳机制作用下，位错运动速率随温度的升高而降低，塑性耗散速率更低。塑性耗散速率的改变会导致氦泡演化的驱动力Gibbs自由能发生改变

图11 不同环境温度下氦泡生长速率对比Fig. 11 Comparison of growth rates of helium bubble at different ambient temperatures

3.2.3 初始位错密度对氦泡演化行为的影响

为探究不同初始位错密度对氦泡生长行为的影响，选取初始位错密度分别为1011和1013m-2，模拟了氦泡生长速率随时间的变化，计算结果如图12 所示。对比氦泡生长速率随时间的变化关系可知，初始位错密度越高，氦泡的生长速率越慢。这仍然可以从能量的观点解释，更多的初始位错将消耗更多的剪切应变能，因此用于驱动氦泡生长的剪切应变能更少。

图12 不同初始位错密度下氦泡生长速率的对比Fig. 12 Comparison of growth rates of helium bubble under different initial dislocation densities

3.3 两个或多个氦泡的聚集行为

Glam 等[17]对比冲击前后铝材料中的氦泡尺寸发现，冲击载荷作用下氦泡尺寸显著增大。根据氦泡演化的物理图像可知，氦泡生长一方面源于拉应力作用下氦泡自身的发展，另一方面则是由于小氦泡聚集融合形成大氦泡，为此模拟了两个或多个氦泡的聚集长大行为。受所使用方法的限制，弹塑性模型仅能模拟动力学系数最大值为500 时的氦泡演化过程，而在模拟两个或多个氦泡时，设置动力学系数为500 时模拟结果显示的氦泡生长行为不显著，因而将动力学系数提高到800，设置温度为600 K 进行模拟，使氦泡的生长行为更加显著。尽管如此，计算结果仍然能够定性地反映两个或多个氦泡的长大聚集行为。

如图13 所示，用序参量η 的分布表示不同相态氦泡与基体的分布，计算结果能够描述两个相邻氦泡的长大聚集过程。尽管两个氦泡的初始位置关于冲击加载方向左右对称，且其他条件完全相同，但是从氦泡的演化过程来看，两个相邻氦泡的演化行为并不完全一样，左氦泡的长大速率略高于右氦泡。考虑到两个氦泡所处的初始条件和加载条件一致，因此推断氦泡生长过程对周围的影响存在一定的范围，当两个氦泡相距足够近时，生长过程中会出现能量竞争现象，进而导致生长速度不一致，即相邻氦泡的演化存在竞争关系。

图13 两个氦泡的长大聚集过程Fig. 13 Growth and aggregation of two helium bubbles

尽管两个氦泡的演化行为存在差异，但是两个氦泡附近的剪应力和局域塑性变形并没有呈现明显的非对称性，包括局域塑性变形、临界分切应力分布等，如图14 所示。对此，分析认为当两个氦泡相距足够近时，氦泡结构非均匀性导致的应力局域化和单个氦泡的作用效果近似一致。

图14 1.0 ns 时刻氦泡附近的可动位错密度与临界分切应力分布Fig. 14 Contours of mobile dislocation density and critical shear stress near helium bubble at 1.0 ns

此外，对比了距离较远的两个氦泡的演化行为，两个氦泡的初始位置仍然关于冲击加载方向左右对称。计算结果表明，距离较远的两个氦泡的长大过程不会出现明显差异，侧面证明了氦泡生长过程对剪切应变能的消耗存在一定的范围，如图15 所示。

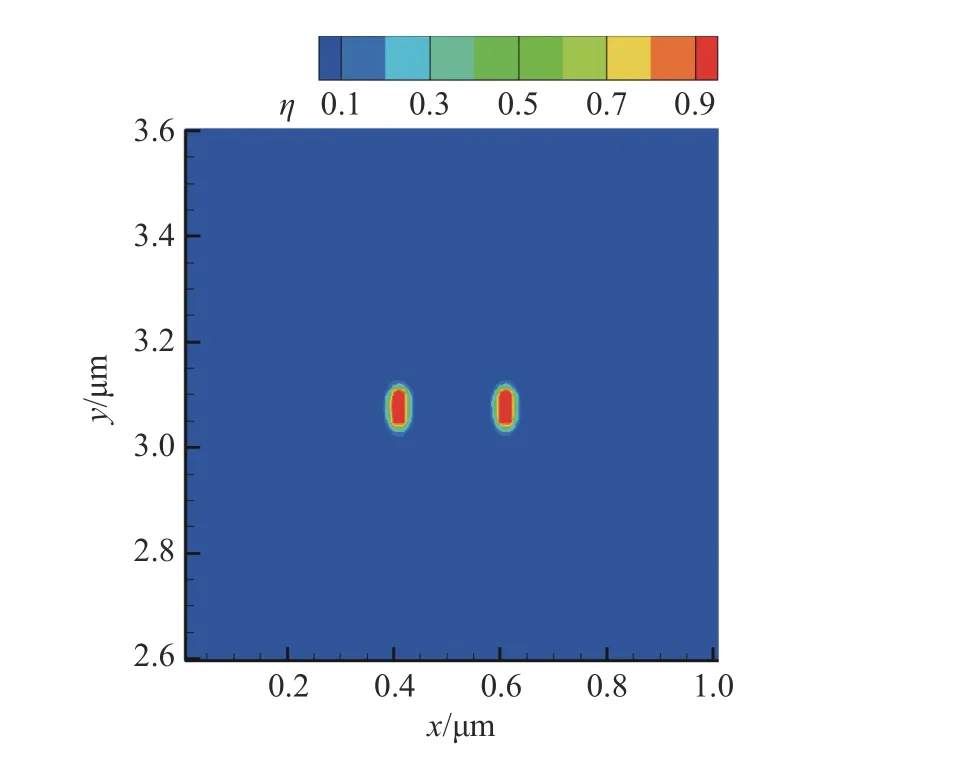
图15 两个氦泡距离较远时1.0 ns 时刻的序参量分布Fig. 15 Distribution of order parameters at 1.0 ns when two helium bubbles are far apart

当预置很多氦泡时，受冲击后氦泡的生长和聚集行为如图16 所示。可以看出，氦泡的演化行为和前面所得结果一致，在压缩波的作用下氦泡几乎不生长，卸载波到达后氦泡尺寸出现明显的变化。从演化结果可以得出：由于氦泡之间的相互作用以及氦泡对周围应力分布的影响，当氦泡较多、分布较密时，氦泡聚集主要发生在冲击波传播方向。

图16 较多初始氦泡时的冲击演化行为Fig. 16 Impact evolution behavior of more initial helium bubbles

4 总 结

基于相场方法建立了可描述冲击下氦泡演化的物理模型，并应用该模型研究了不同外加条件下氦泡的长大行为及其对局域位错集体演化行为的影响。结果表明：氦泡的结构非均匀性会导致局域应力集中和塑性变形集中；在与冲击波相互作用的过程中，局域塑性变形沿冲击波传播方向发射稀疏波，该稀疏波与塑性松弛过程发射的稀疏波共同导致动态屈服应力减小。从氦泡的生长行为来看，氦泡的生长与塑性变形呈竞争关系。在输入剪切应变能一定的情况下，更大的氦泡密度以及更快的生长速率会消耗更多的剪切应变能，导致塑性变形量更小，表观强度更大；反之，更快的塑性变形速率导致氦泡生长更慢，进而使层裂强度更大。尽管如此，由于氦泡本身是一种微观缺陷，因此暂时无法直接将其演化行为与宏观力学响应联系起来。另外，受限于有限元方法处理大变形的能力，目前暂时只能对早期的氦泡演化行为进行研究，无法模拟氦泡聚集并贯通这一物理过程。