基于行业聚类电量曲线分解的中期负荷预测

2022-02-18钟士元张文锦罗路平王伟肖异瑶廖志伟

电力建设 2022年2期

钟士元，张文锦，罗路平，王伟，肖异瑶，廖志伟

(1.国网江西省电力有限公司经济技术研究院，南昌市 330096；2.华南理工大学电力学院，广州市 510641)

0 引言

地区电量数据能及时真实反映当地经济建设和社会生产情况，行业电量数据能直接展示本地不同行业生产规律和发展态势。在2020年新冠疫情期间，地区行业电量统计数据更是第一时间反映了各行业复工复产进度。同时，做好地区行业中长期负荷预测有助于当地供电企业布局电力系统规划、优化电力资源配给以及向用户提供优质定制电力服务，对提高电力系统供电质量有着显著作用。然而，不同行业用电规律各不相同，影响行业电量发展趋势因素繁多复杂且难以统计，历史电量数据样本较小，这些都对精确预测地区行业中长期负荷造成较大阻碍。

中长期负荷预测方法经过长时间的发展，从最初的关注电量自身时间序列周期性规律的指数平滑法[1]、时间序列法[2-3]等，发展到考虑经济因素气象条件对地区负荷电量时间序列影响的回归分析法[4-5]，人工智能算法的兴起[6-7]则将影响因素之间的多维非线性关系纳入考量。文献[8]以最大化原始序列和预测序列的灰色关联度为目标改进灰色预测模型，提高年电力负荷曲线的拟合优度以及预测优度。文献[9]使用果蝇优化算法调整广义回归神经网络参数，提高传统广义回归神经网络对于非线性特性年电力负荷曲线预测准确率。文献[10]整合年月日三种时间尺度的影响因素，通过堆叠长短期记忆网络模型分析多因素跨时间的相互关系，继而提高中长期负荷预测准确率。而另一部分学者通过分解负荷曲线提取特征相对单一的子序列，降低随机因素的影响，选择适合子序列特征的模型分别预测再合成为整体预测序列。文献[11]先通过灰色模型预测得到初步预测电量序列，再用反向传播(back propagation， BP)神经网络对其灰色残差序列进行预测，两者组合预测得出精度更高的预测结果。文献[12-13]使用经验模态分解方法将月负荷曲线分解为不同的本征模态分量，再使用差分整合移动平均自回归模型(autoregressive integrated moving average model, ARIMA)对不同分量分别预测，预测精度比整体ARIMA模型有较大提高。文献[14]使用X-12-ARIMA季节分解模型将月度负荷曲线分解为趋势分量、季节分量以及随机分量，通过协整检验和格兰杰因果检验筛选影响趋势分量变化的关键经济因素，选取气象因素作为随机分量影响因子，分别构建改进支持向量回归模型(support vector regression, SVR)，预测效果有所改善。文献[15]引入奇异谱分析法分解负荷序列，挖掘特殊周期子序列，对子序列建立BP神经网络预测模型，预测精度较季节分解模型有提高。除了数学分解曲线方法外，仍有部分学者通过研究行业负荷用电特性实现地区电量序列分解。文献[16]根据负荷特性曲线聚类地区内用电客户，分析对应影响因素并建立预测模型，将客户预测结果合成为地区预测结果。文献[17]按照工业、商业与居民将地区电量分解，并运用分数阶灰色模型、多元回归模型以及时间序列模型分别预测。文献[18]根据灰色关联度分析不同行业的影响因素并以此聚类，对相同类别的行业电量序列建立深度信念网络预测，提高预测精度。

综合上述文献分析，传统中长期负荷预测侧重于地区整体负荷发展趋势，多数曲线分解方法旨在寻找电量序列不同频率分量，忽视对当地行业发展规律的研究。目前对行业负荷预测研究仍处于对固有大类产业的用电特性研究，并未考虑地区行业转移以及产业升级导致的行业用电趋势显著变动。

因此，本文提出一种基于行业分类与SVR的地区中期负荷分解预测模型。首先，通过计算电量序列周期性按照发展趋势有无发生变动对三大产业下属行业分类。其次，在发展趋势稳定的行业分类中聚类分析相似用电特性的行业，通过季节分解分离聚类行业电量序列；对于发展趋势变动行业，截取突变后的电量序列作为训练数据。最后，针对不同电量序列建立对应SVR预测模型，以江西省某市用电量数据验证行业分类算法的有效性和预测模型的准确性。

1 行业发展趋势与行业分类

根据2011年版《国民经济行业用电分类》，可以将一个地区的社会生产总用电分为城乡居民用电和一二三产业四大类，在此基础上进一步划分为54个行业用电分类。因为每个地区的经济发展水平和经济发展重心不同，不同地区的不同行业用电特性也不尽相同。另外，由于当地政府区域发展政策变动，可能存在部分行业转移至其他地区或者进入快速发展时期，行业用电特性发生显著变化，因此需要在行业聚类分析之前通过行业周期性分析对发展趋势有无突变的行业进行分类。

1.1 基于DTW相似度的行业周期分类

在行业电量周期性计算中，除行业发展周期与当地政策变动的宏观因素以外，计算结果容易受到工厂订单和“春节效应”[19]的影响而产生波动，从而导致行业电量周期性判断错误。为降低此类情况的影响，在行业电量周期性计算中引入鲁棒性较高的动态时间规整(dynamic time warping, DTW)算法。DTW算法侧重于比较时间序列的发展趋势，通过动态规划思想求解两个时间序列之间的规整路径距离从而判断序列相似性。

假设某行业相邻年份归一化电量序列分别为X=[x1,x2,…,x12]和Y=[y1,y2,…,y12]，D为12×12规整距离矩阵，则该行业DTW相似度计算如下：

(1)

D(i,j)=d(xi,yj)+min[D(i-1,j),
D(i,j-1),D(i-1,j-1)]

(2)

(3)

式中：D(i,j)为累积规整距离；d(xi,yj)为xi和yj两点之间距离；θ为通过规整距离D(12,12)计算得到的DTW相似度。

图1为部分代表行业电量曲线对比图，其中行业a与行业b发展趋势相似，在保持全年基本高负荷生产规律的同时以相似的增长率上升；而行业c则在2016年后发展陷入颓势，并在2018年全年生产规律发生变化。

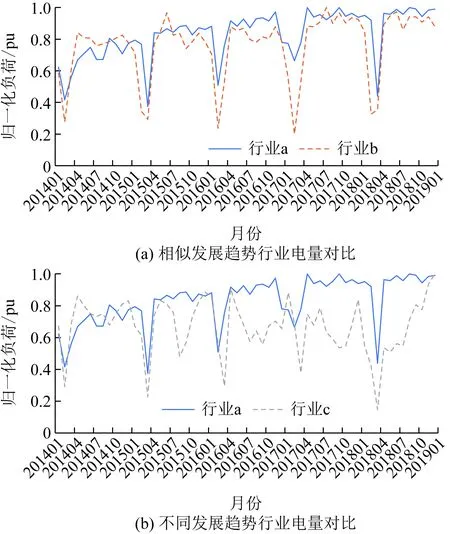
图1 部分代表行业电量曲线对比Fig.1 Comparison of electricity consumption curves of some representative industries

分别计算3个行业相邻年份的DTW相似度均值、皮尔逊相关系数均值以及余弦相似度均值作为行业周期性指标，其计算结果对比如表1所示。由表1可知，余弦相似度计算结果普遍偏高，不能有效区分行业电量周期性；皮尔逊相关系数反映点对点的映射关系，在工厂订单波动和“春节效应”的影响下，行业a的周期性计算结果显著降低至与行业c结果接近，导致对行业a周期性的误判；DTW相似度侧重于通过比较电量曲线形状相似性判定电量序列发展趋势，对工厂订单波动和负荷低谷变动的敏感性最低，从而更易区分发展趋势变动的行业。

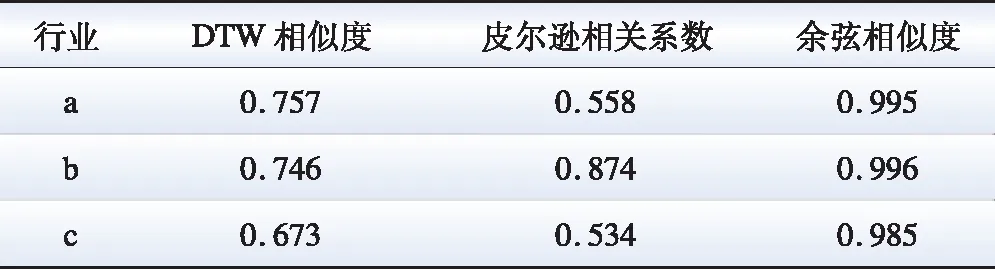
表1 部分行业的不同周期性指标对比Table 1 Comparison of different cyclical indicators for selected industries

因此，选择对随机波动鲁棒性更高的DTW相似度作为行业电量周期性评价指数，通过计算行业电量过往相邻年份DTW相似度均值评判行业发展趋势是否出现变动。

为方便本文描述，对行业周期性区分作如下定义：行业发展趋势稳定的强周期行业、行业发展趋势发生变化的弱周期行业以及受订单主导的无明显周期行业。经过对多个地市的多个行业电量数据统计分析，选取不同周期代表行业如图2所示。结合皮尔逊相关系数判定依据分析，选择具体判定指标如表2所示。

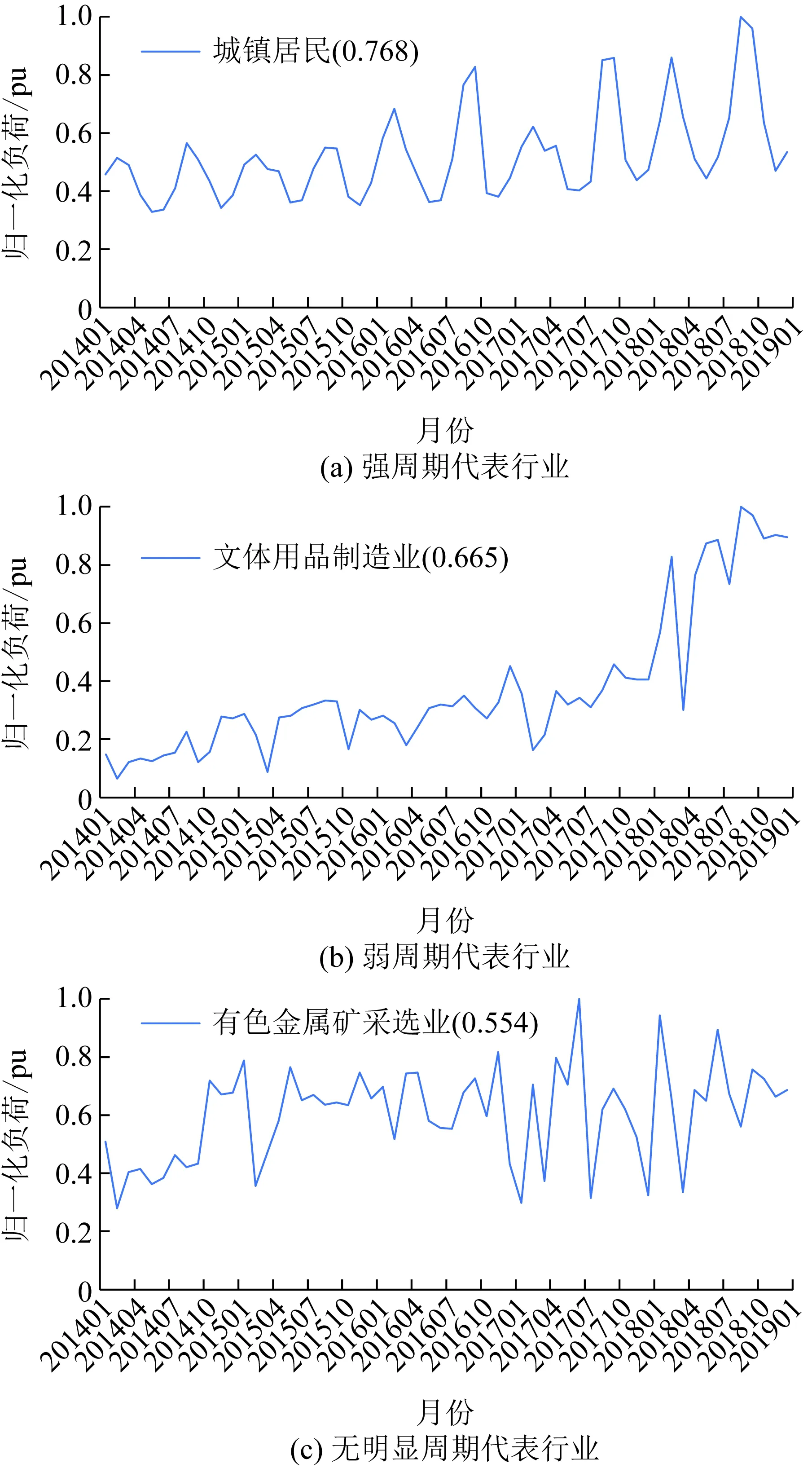
图2 不同周期性代表行业Fig.2 Representative industries of different periodicity

表2 行业周期性指标Table 2 Industry cyclical indicators

1.2 行业电量k-means聚类

在对行业周期性分类后，为区分强周期行业的发展趋势，需要按用电特性对不同产业的强周期行业聚类分析。考虑到第三产业的绝大多数行业与城乡居民生活紧密联系，所以将城乡居民用电和第三产业行业用电合并为同一产业进行聚类分析。

本文采用基于欧氏距离的k-means聚类算法，通过计算不同聚类数目k的误差平方和(sum of squared error, SSE)运用手肘法选择最佳聚类数，算法步骤如下：

步骤1：输入强周期行业电量原始数据，去除显著离群数据，并作归一化处理。

步骤2：对城乡居民用电和第三产业行业用电数据随机选择2个聚类中心，计算各电量序列到聚类中心距离，并将各电量序列归入最近聚类中心类别。

步骤3：重新计算电量序列聚类中心，若出现偏移则重复步骤2，若聚类中心收敛则计算并记录该聚类数下的SSE。

(4)

(5)

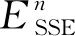
步骤4：增加聚类数目，重复步骤2—3直至聚类数目达到上限，根据SSE与聚类数曲线图，选择变化曲率最大的点，对应聚类数为最佳聚类数。

步骤5：分别对第一产业和第二产业行业电量作上述聚类处理，确定最佳聚类结果。

2 中期负荷预测模型

本文提出的预测模型流程如图3所示，图3中：YS、YW分别为强、弱周期行业电量序列；TS、SS、RS分别为强周期行业电量序列分解的长期趋势分量、季节周期分量以及无规则余项分量；T′S、S′S、Y′W分别为对应电量序列的预测结果。

对地区行业月度电量序列进行电量周期性分类，根据DTW相似度判定行业电量的周期性，分别对三大产业下属行业电量按强周期、弱周期以及无明显周期分类。由于不同周期性分类的行业电量序列规律性不同，因此本文采取对应不同的预测方法。对于强周期行业电量序列，通过季节分解将其聚类电量曲线分解为长期趋势分量、季节周期分量以及不规则余项分量，然后运用SVR对趋势分量和周期分量进行预

图3 中期负荷预测流程Fig.3 Medium-term load forecasting

测；对于弱周期行业电量序列，通过截取行业发展趋势变化后的电量数据进行SVR预测；对于无明显周期行业，由于该类行业通常为当地小微企业，受订单波动影响较大，本文暂不对其预测，作残差处理。

2.1 季节趋势分解

考虑到强周期行业用电的规律性和部分行业在特定生产时期出现的离群值，本文选择基于局部加权回归(locally weight regression，LOESS)的时间序列季节分解方法(seasonal-trend decomposition procedure based on LOESS, STL)作为强周期行业电量序列的季节趋势分解方法[20]。

STL算法是一种加法模型的时间序列分解方法，通过内外双循环的机制实现不同分量的分离与计算。在STL算法中，内循环负责趋势拟合与周期分量计算，而外循环负责内循环鲁棒性权重的计算，内外循环嵌套迭代实现长期趋势分量、季节周期分量以及不规则余项分量的分离，计算过程如下：

Yi=Ti+Si+Ri

(6)

(7)

(8)

(9)

(10)

为避免不规则余项分量受离群值影响过大，在外循环重新计算鲁棒性权重，公式如下：

(11)

(12)

(13)

式中：B(u)为鲁棒性权重计算二次函数，其中u表示对应自变量；h为修正变量，其中median表示取中位数。

2.2 SVR原理

作为一种监督学习模型，SVR由于其数据需求少、泛化能力高以及能够非线性拟合等优点，被广泛应用于多种时间序列预测中。在本文中，SVR不仅适用于强周期行业电量序列长期趋势分量与季节周期分量的线性回归问题，而且适用于弱周期行业电量序列训练数据样本较少的情形。

为分析本文各电量序列输入输出映射关系，寻找结构风险最小化的电量超平面，对本文涉及的线性回归问题以及优化问题作如下定义：

f(x)=(w·x)+b

(14)

(15)

(16)

引入拉格朗日算子，将原线性约束问题松弛为无约束问题，并通过求解得出最终回归参数，对应回归函数g(x)为：

(17)

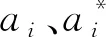
3 算例分析

本文选择2014年1月至2019年12月江西省某市月度行业用电量数据作为算例分析。文中实验的所有数据处理与预测过程均在Python3.8.3、CPU i5-6500环境中完成编程计算。

3.1 行业分类和聚类结果分析

利用DTW相似度对行业电量序列进行分类，将地区行业月度电量序列分类为行业发展趋势稳定的强周期行业、行业发展趋势发生变化的弱周期行业以及受订单主导的无明显周期小微行业，对应行业年用电量平均占比依次为88.37%、11.32%以及0.24%。运用k-means聚类算法对强周期行业在各自产业归属下进行聚类，聚类中心结果如图4所示；按照行业发展趋势变化类型不同将弱周期行业分类，分类结果部分代表行业如图5所示；由于无明显周期行业多为当地小微企业，受订单多少影响明显，用电量波动幅度较大且占地区总用电量比重极小，因此本文对其作残差舍去处理。

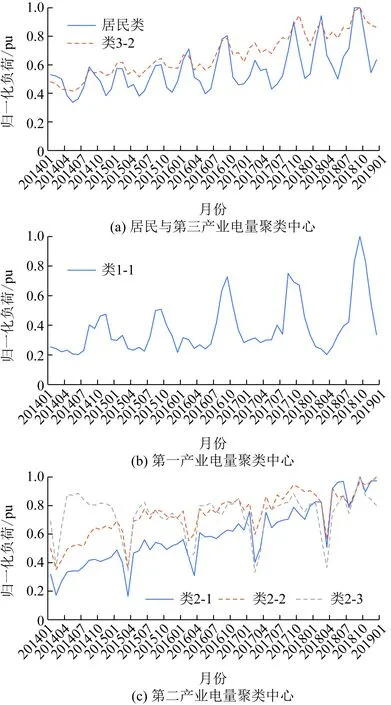
图4 强周期行业电量聚类中心Fig.4 Cluster centers of strong periodic industrial power consumption

由图4可以看出，城乡居民用电和第三产业行业用电可分为两类，其中居民类以城乡居民用电为聚类中心，下属行业均与城乡居民生活密切相关，该类行业用电曲线具有显著的季节峰谷特性以及与当地生活水平同步的增长率，而类3-2行业则是在保持基本相同增长率的同时没有明显的季节峰谷差别。第一产业中的强周期行业用电特性表现为显著的夏季用电高峰特性，与传统农忙时节相吻合。在第二产业中，强周期行业可分为快速增长型的类2-1、较快增长型的类2-2以及基本持平型的类2-3，三种类型的行业用电特性除电量增长率不同外，均保持全年用电高峰，且都受“春节效应”影响，在春节期间具有明显的用电低谷特征。

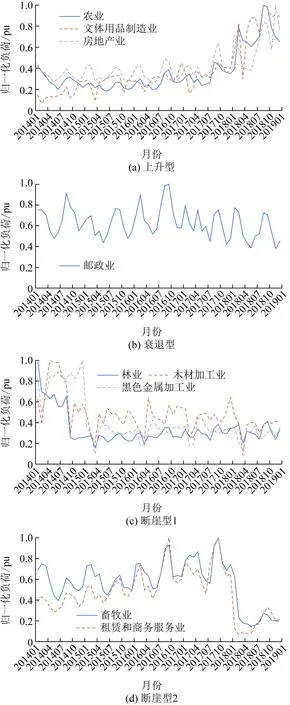
图5 弱周期行业分类部分行业电量曲线Fig.5 Electricity consumption curve of some industries in weak periodic industry classification

由图5可以看出，弱周期行业主要分为以下3种：以房地产为代表的上升型行业在2017年迎来行业快速发展期；邮政业作为衰退型行业在2017年进入行业衰退期；而第三类行业则是由于当地的政策变动分别在2015年和2018年出现用电量断崖式下跌。

3.2 中期负荷电量预测效果对比

以该市2019年月度用电量作为预测对象，选择文献[13]所提的经验模态分解法、文献[14]所提的季节分解法以及文献[17]所提的传统城乡居民与三大产业分解法，分别作为本文电量序列分解对比方案一二三，预测模型均采用SVR。

选择平均绝对百分比误差EMAPE(mean absolute percentage error, MAPE)和均方根误差ERMSE(root mean square error, RMSE)作为本文的预测模型精度评估指标：

(18)

(19)

式中：Yi、Y′i分别为第i个月地区电量的真实值与预测值；n为月份数，n=12。

本文所提方法与对比方案对该市月度用电量预测结果如图6所示，相对误差对比如表3所示。

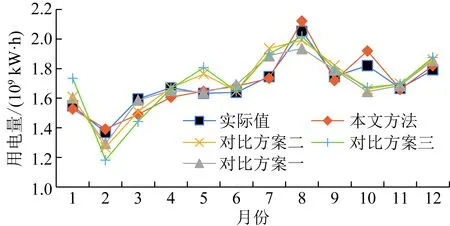
图6 月度电量预测结果Fig.6 Forecasting results of monthly electricity consumption

由图6可以看出，相较于对比方案预测结果，本文方法的预测偏差相对较小，对于趋势变动明显的7月与10月，本文方法的预测趋势与实际用电量趋势相同。如表3所示，本文方法大多数月份预测相对误差绝对值最小，最大相对误差绝对值最小，且相对误差绝对值超过5%的月份数也少于对比方案。可见本文方法在中期负荷预测的准确度与稳定性方面均优于对比方案。

本文方法的EMAPE为2.50%，ERMSE为5.36×108kW·h，对比方案的EMAPE依次为3.72%、4.81%、6.21%，ERMSE依次为8.27×108kW·h、9.77×108kW·h、12.24×108kW·h，这说明本文方法通过行业周期性分类后聚类地区行业电量序列引入行业自身发展趋势的影响，对于SVR预测模型的预测精度有所提高，而且对于用电量增长趋势预测更为准确。