富水砂层地下水位变化对盾构隧道衬砌结构的影响分析*
2022-02-18曹鹏飞袁宗义陈昭阳邱友根陈祥胜石钰锋
曹鹏飞 袁宗义 陈昭阳 邱友根 陈祥胜 石钰锋,
(1.南昌轨道交通集团有限公司,330038,南昌;2.中交第四航务工程勘察设计院有限公司,510290,广州;3.华东交通大学轨道交通基础设施性能监测与保障国家重点实验室,330013,南昌∥第一作者,高级工程师)
0 引言
在富水砂层中,由于地下水位升降速率存在差异,以不同速率升降的地下水对土体产生不同的渗流力,引起盾构隧道衬砌内力变化,对隧道产生不利影响。因此,有必要针对地下水位变化速率对盾构隧道衬砌应力的影响进行分析。
文献[1]结合数值模拟和现场实测数据分析研究,发现水位变化对隧道上浮值波动幅度影响较大;文献[2]进行了三维应力-孔隙压力耦合有限元分析,证实了地下水位下降和过度沉降之间的直接联系;文献[3-4]采用复变函数理论,提出了地下水升降影响下盾构隧道开挖引起的周围地层、衬砌变形和应力计算方法,指出水位下降过程中,隧道上方土体的有效应力显著增大;文献[5-6]对高水压条件下盾构隧道管片力学特征进行分析,得出管片在水压情况下的破坏规律以及管片内力大小和分布特征;文献[7]通过理论分析、模型试验以及现场实测数据分析,得出水下复合式衬砌的水压特征;文献[8]针对国内4种典型盾构隧道,分析了不同覆土条件下水位变化对管片内力的影响,指出砂卵石地层中管片弯矩随水位升高不断减小;文献[9]结合隧址区的地形地质及水文条件对施工期作用在盾构主体结构上的水压力进行了现场跟踪测试,得出了施工期外水压力的分布规律;文献[10]依托新圆梁山隧道工程,采用数值分析方法研究了3种隧道衬砌断面在全环均匀水压力下的内力分布特征,发现在不同的衬砌结构形式下,衬砌轴力值和弯矩值与水压力均呈线性关系,不同衬砌断面形式下轴应力相差不大;文献[11-12]针对高水压盾构隧道进行了数值计算和分析,指出在高水压作用下衬砌结构的受力和变形都较大,衬砌结构上存在较大的纵向弯矩;文献[13]通过试验及数值模拟分析不同降雨强度下隧道结构的受力和变形,发现降雨入渗后隧道结构变形和受力增加明显,其中,拱顶沉降增幅达到46%,隧道初期支护应力增加20%~27%;文献[14]采用FLAC 3D软件和Cam-Clay模型分析不同潜水水位或受限承压水位下的地面沉降和隧道衬砌内力,在潜水水条件下,考虑渗流的最大沉降值比不考虑渗流的沉降值高50%;文献[15]采用数值法对曼谷地铁延长线穿湄南河隧道在不同的排水状态下围岩的孔隙水压力以及隧道衬砌内力的分布规律进行了分析;文献[16]对矿井支护的静水压力进行了研究;文献[17]通过对首尔地铁5号线水下隧道工程研究,得出渗流力对衬砌的影响。
上述研究,针对盾构隧道在不同水压状况及地下水位变化的条件下,对隧道管片的内力及沉降进行了研究及分析。但大多未体现地下水位不同升降速率对隧道衬砌内力的影响。本文依托南昌市某既有地铁隧道工程,采用数值模拟手段,并根据南昌地区水位升降规律,拟定若干工况,分析地下水升降速率对盾构隧道衬砌内力的影响情况。
1 工程概况
1.1 隧道衬砌结构参数及周边环境
南昌某地铁区间隧道位于砂土层,其特点是含砂量大且非砂和小卵石含量小于10%,邻近赣江和碟子湖,故地下水丰富。隧道外径为6.2 m,衬砌采用C50钢筋混凝土,厚度为30 cm;环宽1.2 m,隧道埋深为15.4~21.4 m。其地层剖面图如图1所示。
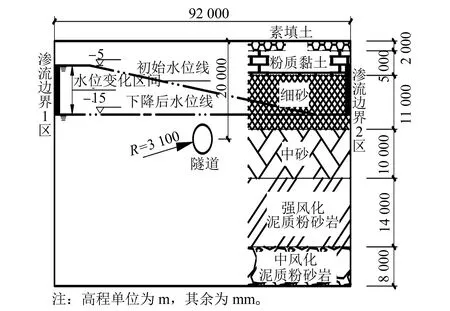
图1 南昌某地铁隧道地层剖面图
1.2 水文条件
该工程位于南昌市东北部,距离赣江约1 500 m,距离碟子湖约2 700 m。赣江汛期一般为4~6月份,受长江水位影响,水位涨落历时长,升降速率较小,水位升降幅度达3~13 m。8月以后,水位开始缓慢消退;10月至次年3月为枯水期,碟子湖为赣江及瀛上河的调洪湖泊,汛期调洪时水位升降幅度达 2~14 m,速率最高可达1.8 m/d。该地区砂层渗透系数为 75~120 m/d。
2 渗流分析
2.1 模型建立
由于该地区雨水充足,地下水流动速率较大,地铁隧道常年受地下水影响,因此有必要对既有运营隧道受不同升降速率的地下水影响的特征进行分析。
采用Plaxis软件建立有限元模型,对隧道某一截面进行流固耦合分析。因地下水实际分布平缓,为较准确地模拟地下水渗流和消除模型尺寸效应,故假定所有工况下模型中的地下水按所设水位由左向右流动。取模型尺寸X方向为隧道直径的15倍(即92 m),Y方向为隧道直径的8倍(即50 m),隧道外径为6.2 m,衬砌厚度为0.3 m。土层从上往下依次为素填土、粉质黏土、细砂、中砂、强风化泥质粉砂岩和中风化泥质粉砂岩,共6层。隧道周边土体及衬砌采用网格加密处理,模型底部及侧面约束位移,如图2所示。在各工况中,对地下水渗流边界1、2区设置相应渗流边界条件。模型的地下水位标高邻近碟子湖为-5 m,邻近赣江水位标高为-15 m,盾构隧道始终处于地下水位以下。
2.2 工况拟定
碟子湖水位升降幅度达2~14 m,速率最高可达1.8 m/d,且砂层渗透系数较大,由此建立的工况如表1所示。
表1工况中上升10 m是指模型左侧地下水位由-15 m上升至-5 m,下降10 m是指模型左侧地下水位由-5 m下降至-15 m。当地下水上升时,渗流边界1区为流入边界,渗流边界2区为流出边界;地下水下降时,渗流边界1区为不透水边界,渗流边界2区为流出边界。渗流边界1、2区如图2所示。
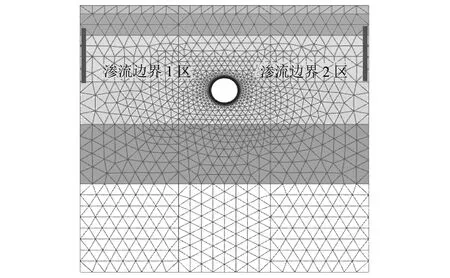
图2 南昌某地铁隧道有限元模型图

表1 计算工况
因该隧道为既有运营隧道,故建模时先对隧道土体进行开挖及施作衬砌,待周边土体进行应力重分布、变形和地下水平衡后,对模型进行位移清零。继而分别对各工况进行计算分析。
2.3 本构模型及参数选取
计算模型的各土层采用HS-small材料模型,隧道衬砌采用实体单元模拟,各土层及隧道衬砌参数取值如表2所示。

表2 土体参数
2.4 测点布设图
为方便后期分析衬砌受力情况,将衬砌网格划分为6层,并选取拱顶、右拱肩、左拱脚和左拱肩4个位置进行分析,标号分别为a、b、c、d,如图3所示。

图3 隧道衬砌实体单元细部图
3 模型正确性验证
分别选取某断面9~10月份(历时28 d,水位下降9.6 m)和5月1日至5月16日(汛期调洪阶段,历时16 d,水位上升10.5 m。),共44 d的隧道衬砌在地下水影响下拱顶的沉降、水平位移和隧道水平腰线收敛监测数据,与有限元模拟地下水下降速率为0.33 m/d和上升速率为0.67 m/d时的结果进行对比,以验证模型的正确性。
图4为地下水下降速率为0.33 m/d时,拱顶a点处沉降监测值与数值模拟值曲线图。如图4 a)所示,拱顶沉降最大计算值为1.42 mm,监测值约为1.45 mm;如图4 b)所示,拱顶最大水平位移的计算值为0.43 mm,监测值约为0.38 mm;如如图4 c)所示,隧道水平腰线最大收敛值的计算值为0.94 mm,监测值约为0.92 mm。其他计算值相对监测值都有一定的增减幅度。

图4 水位下降速率为0.33 m/d时拱顶监测值与计算值对比曲线图
图5为地下水上升速率为0.67 m/d时,拱顶a点处沉降监测值与数值模拟值曲线图。如图5 a)所示,拱顶沉降最大值的计算值为1.56 mm,监测值约为1.58 mm;如图5 b)所示,拱顶最大水平位移的计算值为0.72 mm,监测值约为0.79 mm;如图5 c)所示,隧道水平腰线最大收敛值的计算值为1.21 mm,监测值约为1.15 mm。其他计算值相对监测值同样都有一定的增减幅度。

图5 水位上升速率为0.67 m/d时拱顶监测值与计算值对比曲线图
但考虑到监测的可允许误差,拱顶的沉降监测值及水平位移值与模型计算值总体吻合,且变化趋势一致,表明该数值模拟基本合理。
4 计算结果分析
4.1 衬砌轴力和弯矩分析
图6~7分别为高、低水位情况下,隧道衬砌的弯矩和轴力分布图。由图6~7可知,地下水位在不同位置时,衬砌最大弯矩及其轴力均位于拱腰,且衬砌左侧弯矩及其轴力相对较大,其值分别为-120.5 kN·m、-116.2 kN·m、732.6 kN、710.4 kN、-145.3 kN·m、-134.8 kN·m、656.1 kN、652.3 kN。高水位时,衬砌的轴力相比低水位时较大,但弯矩较小。

图6 高水位时衬砌弯矩、轴力分布图
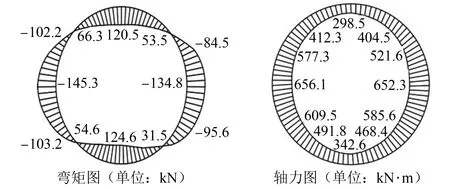
图7 低水位时衬砌弯矩、轴力分布图
4.2 轴力值分析
表3~6分别为拱顶、右拱肩、左拱脚和左拱肩的轴力值。由表3~6的数据可知:轴力随水位上升不断增加,随水位下降不断减小,且水位以不同速率在上升或下降时,轴力变化一致。

表3 拱顶a点轴力值
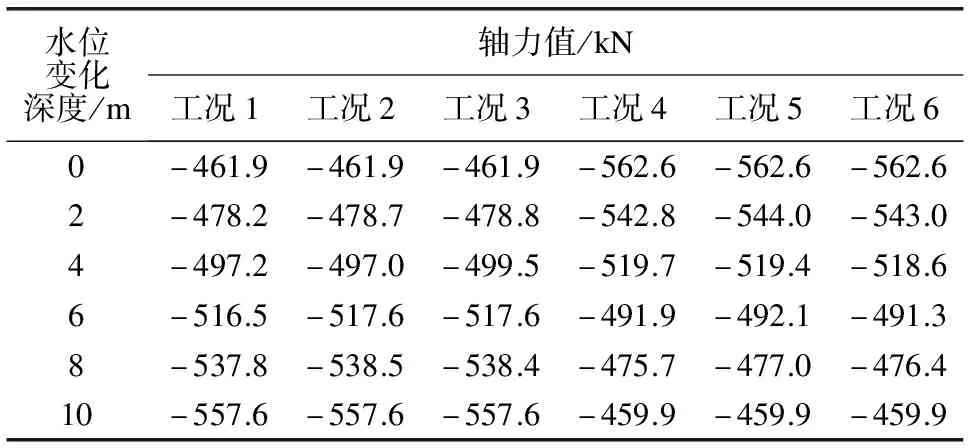
表4 右拱肩b点轴力值
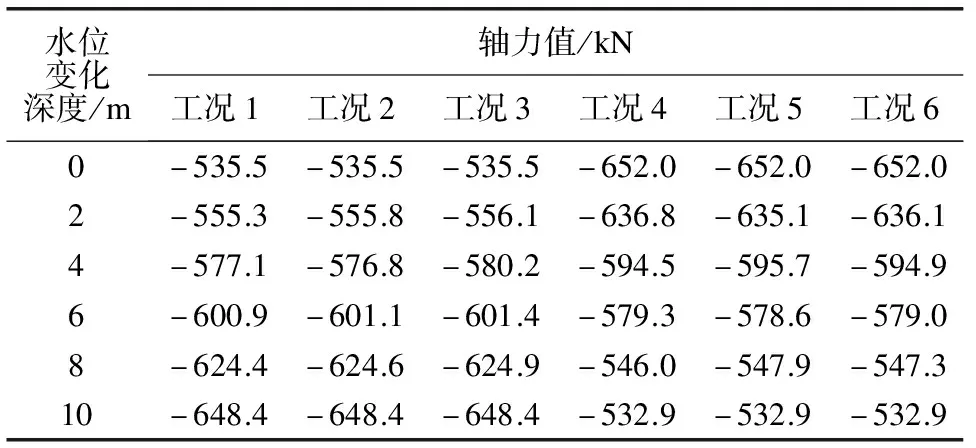
表5 左拱脚c点轴力值
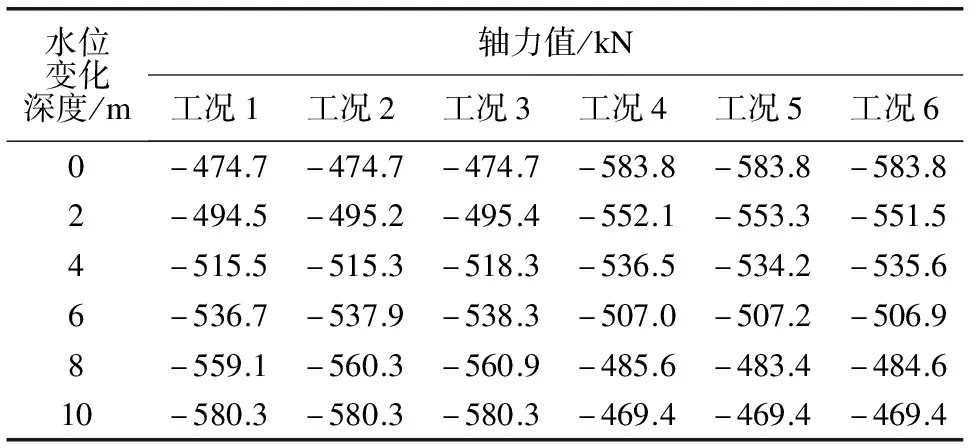
表6 左拱肩d点轴力值
4.3 弯矩分析
图8~11分别为隧道衬砌拱顶、右拱肩、左拱脚、左拱肩弯矩变化曲线图。

图8 拱顶a点弯矩变化曲线图

图9 右拱肩b点弯矩变化曲线图
1)由图8 a)、9 a)、10 a)、11 a)可知:弯矩均随地下水位上升不断减小,且各工况下弯矩变化曲线存在差异。弯矩绝对值大小关系为:工况1>工况2>工况3。各点弯矩相对工况3的增量如表7所示。
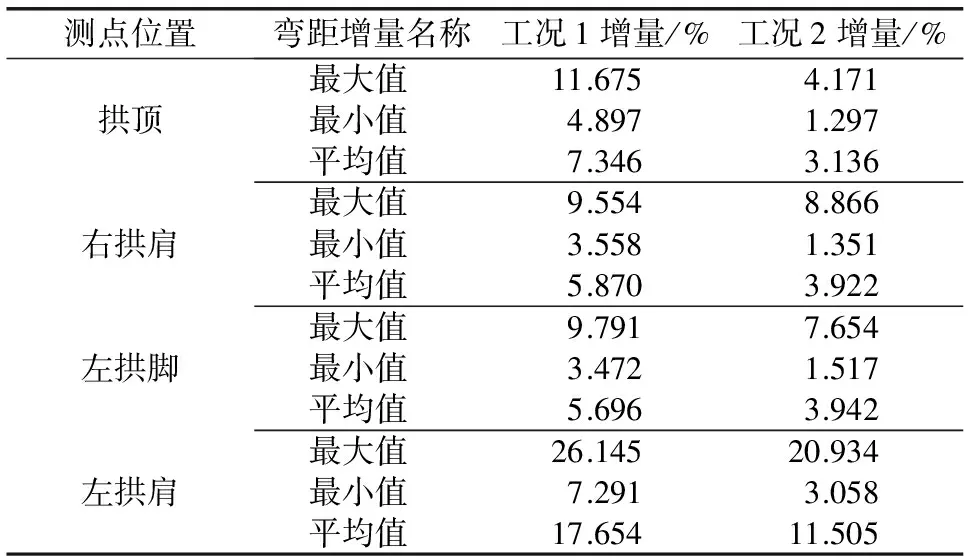
表7 地下水位上升时相对工况3的弯矩增量
2)由图8 b)、9 b)、10 b)、11 b)可知:弯矩均随着地下水位下降不断增加,且各工况下的弯矩变化曲线存在差异。弯矩绝对值大小关系为:工况4>工况5>工况6。各点弯矩相对于工况6的增量如表8所示。
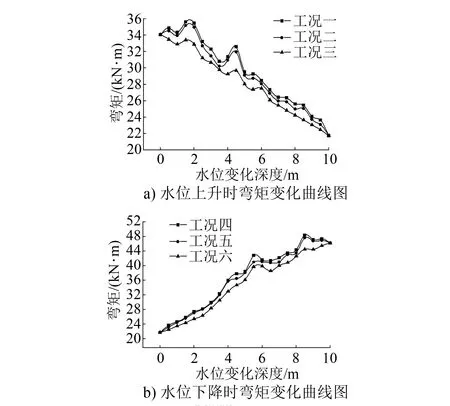
图10 左拱脚c点弯矩变化曲线图

图11 左拱肩d点弯矩变化曲线图
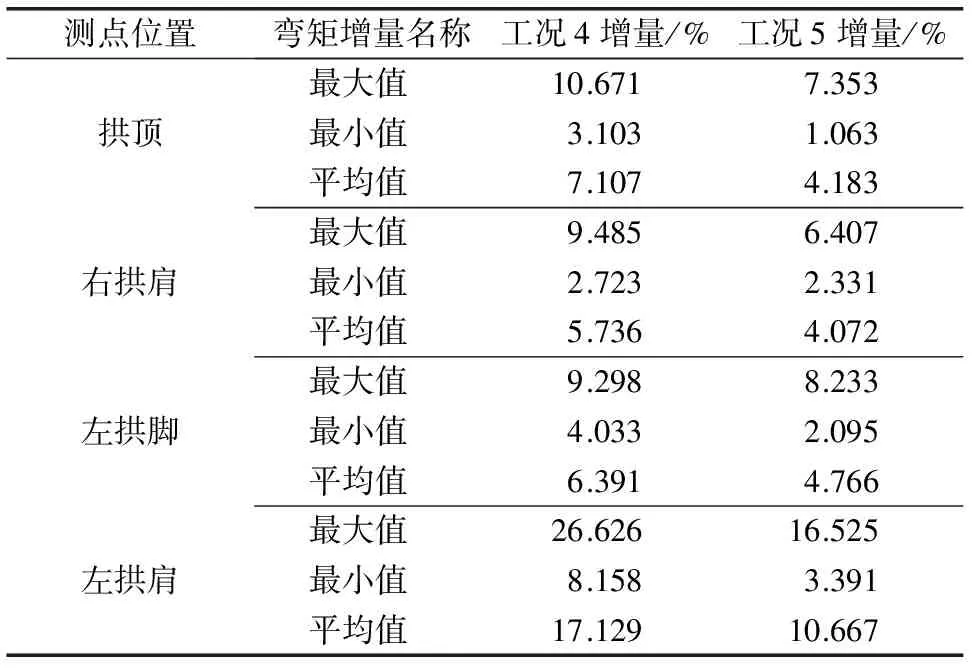
表8 地下水位下降时相对工况6的弯矩增量
3)地下水位于-15 m时,由水位下降所得弯矩相比水位上升,在拱顶a点处增大30.5%,在右拱肩b点处增大36.7%,在左拱肩d点处增大34.2%,在左拱脚c点处增大35.7%。平衡后,各点弯矩增量近似为0。当地下水位于-5 m时,各点弯矩在不同工况中近似相等。
5 结论
1)地下水以不同速率升降时,对盾构隧道衬砌结构的内力影响不同。水位上升,弯矩减小;水位下降,弯矩增大。
2)水位以不同速率上升或下降10 m时,对衬砌初始和最终弯矩无影响,但对其变化过程有一定影响。
3)当水位升降速率大于0.33 m/d时,下降过程对衬砌弯矩影响大于上升过程,且当水位平衡于某点时,下降过程所得弯矩大于上升过程。
4)当地下水升降速率范围为0~0.33 m/d时,对盾构隧道衬砌内力弯矩影响较小;当速率大于0.33 m/d时,对隧道衬砌内力影响较大,且随着速率增加,对衬砌内力的影响不断增大。
