内置式泵房轨道系统的轨道参数敏感性分析*

2022-02-18傅承诚崔信为

城市轨道交通研究 2022年1期

傅承诚罗望崔信为时瑾

(1.绍兴市柯桥区轨道交通集团有限公司，312030，绍兴；2.北京交通大学土建学院，100044，北京∥第一作者，高级工程师)

内置式泵房轨道系统是一种比较新颖的泵房轨道结构，取消了隧道间的联络通道，将废水泵房设置在道床内部，降低了施工的风险和难度，在复杂线路中的特殊地段有着广泛的应用。

采用内置式泵房后，由于轨道断面发生了变化，其实际服役可靠性值得关注。很多学者对轨道结构可靠性开展了大量研究，文献[1]对已有的响应面分析法进行了改进，解决了在对桥梁结构的可靠度进行分析时结构功能函数未知的问题。文献[2]分析了关键因素对桥上嵌入式轨道无缝线路力学特性的影响，提出了桥上嵌入式轨道无缝线路可靠性评估方法，为嵌入式轨道结构的设计提供理论指导。文献[3]建立了列车荷载与温度荷载共同作用下CRTSⅡ型轨道板混凝土疲劳功能函数，得出了一种精度较高的CRTSⅡ型轨道板疲劳可靠度的计算方法。值得指出的是，目前对内置式泵房轨道结构可靠性问题的研究较少。

鉴于当前内置式泵房轨道技术尚不成熟，本文主要依托杭州至绍兴城际铁路工程(以下简称“杭绍线”)内径5.9 m盾构区间，开展轨道关键技术和设备布局等的研究，解决实际工程中存在的技术瓶颈。因此，分析内置式泵房轨道系统的参数敏感性、评估其服役可靠性与安全性有着重大的工程意义。

1 理论模型及结果分析

1.1 工程背景

杭绍线起自杭州地铁5号线香樟路站，终到绍兴市笛扬路站，与绍兴轨道交通1号线贯通运营融入绍兴主城区。线路全长20.3 km，设站10座(其中地下站6座)区间风井2座，地下区间5处。

杭绍线采用了内径5.9 m盾构技术[4]，线路几处最低点联络通道和废水泵房合建存在施工风险。为规避土建施工风险，拟在部分区间采用内置式泵房轨道方案。

1.2 有限元模型及计算参数

本文基于已有的工程背景，在建立有限元模型时，将60 kg/m的钢轨简化成工字型梁，扣件间距为0.6 m；隧道内布置3块整体道床，每块长12.5 m，道床间设置0.2 mm伸缩缝[5]。计算泵房排水能力后，设计泵房尺寸为：14.4 m(长)×0.8 m(宽)×0.6 m(高)。道床下部设置接触单元与盾构壁连接。为了更好地反映道床与盾构壁之间的相互作用，假定接触面垂向只有在压紧状态下才会传递法向力的硬接触，水平方向采用库仑摩擦系数为0.5的有限滑移接触[6]。

钢轨采用60 kg/m轨，扣件采用TSD1型扣件，轨枕间距为0.6 m，隧道基础厚度0.35 m，采用C50混凝土，相关参数如表1所示。利用有限元计算软件建立地铁盾构区间内置式泵房轨道模型，其中钢轨采用梁单元模拟，扣件采用弹簧阻尼单元模拟，整体道床和底部盾构壁均采用实体单元模拟[7]，有限元模型如图1所示。

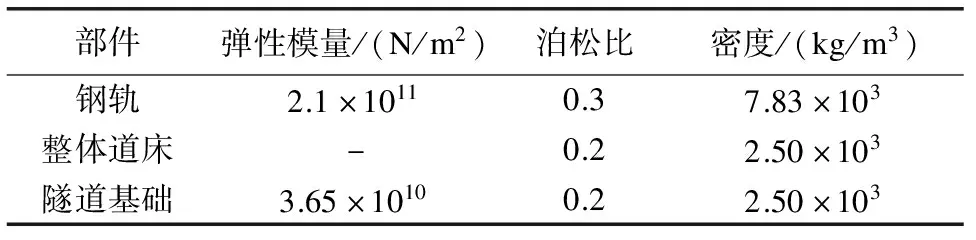
表1 轨道计算参数

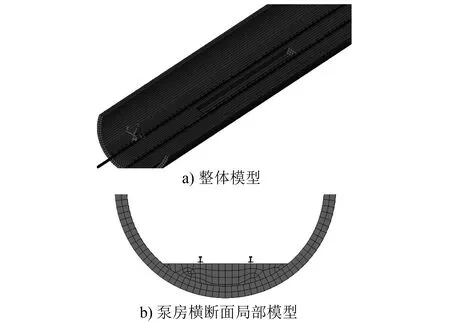
图1 盾构隧道区间内置式泵房轨道结构模型

移动荷载采用地铁B型车。车辆轴重为14 t，车辆定距为12.6 m，转向架轴距为2.2 m，车体长度为19 m，车箱间距为0.45 m，由此计算两节车中间最近的两个车轴之间的距离为4.65 m。列车垂向荷载分布如图2所示。

图2 列车垂向荷载分布图

1.3 轨道动力响应分析

列车荷载作用下，钢轨和轨道板会产生一定的垂向和横向变形。采用垂向加速度与垂向位移作为轨道结构振动强弱指标。DB11/T 1714—2020《城市轨道交通工程动态验收技术规范》中指出：整体道床类减振轨道在列车动力作用下，钢轨的最大垂向位移不应大于4 mm，垂向加速度不应大于2 500 m/s2，整体道床的最大垂向位移不应大于3 mm[8]。

图3～5为计算得到的变形图，从图中可以看出：设置内置式泵房的轨道结构，在跨中截面，钢轨的垂向位移为0.55 mm，钢轨的垂向加速度为20 m/s2，整体道床的垂向位移为0.09 mm，均未超过规范限值，且具有较大的余量。这说明内置式泵房轨道结构的安全性满足使用要求。

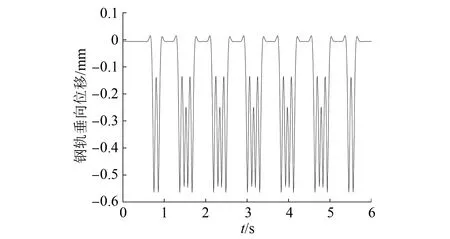
图3 钢轨跨中截面垂向位移

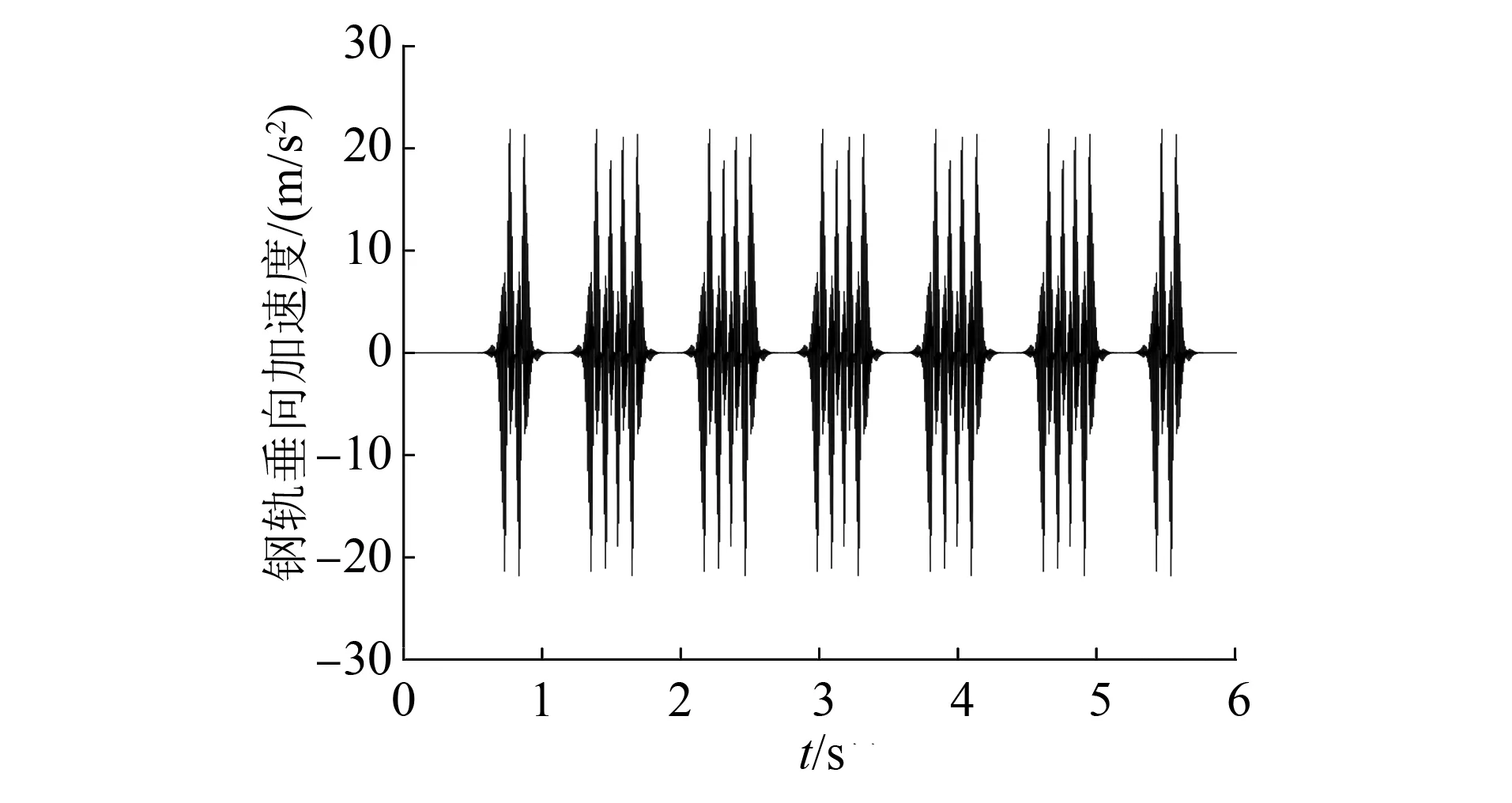
图4 钢轨跨中截面垂向加速度

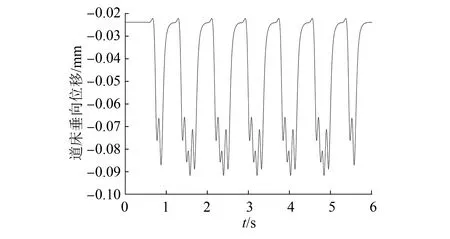
图5 道床跨中截面垂向位移

2 轨道结构参数敏感性分析

2.1 随机参数选取

选取道床跨中截面的横向弯矩为评价指标，对内置式泵房轨道结构的参数敏感性进行研究。结合实际工程项目，初步拟定的随机参数为道床弹性模量、扣件垂向刚度、扣件横向刚度和扣件横向阻尼。这4个随机参数高低水平取值均根据我国常用范围选取[9-15]。

采用24-1析因实验设计研究内置式泵房轨道系统的参数敏感性，将筛选出的随机参数的高低水平取值罗列出来，如表2所示。

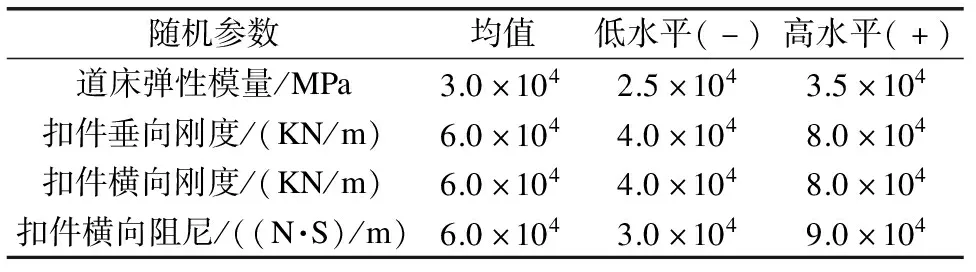
表2 内置式泵房轨道结构随机参数

对于选中的随机参数，根据表2取值进行输入，分别计算8组不同的随机变量组合下整体道床横向弯矩和整体道床横向位移的数值，计算结果如表3所示。

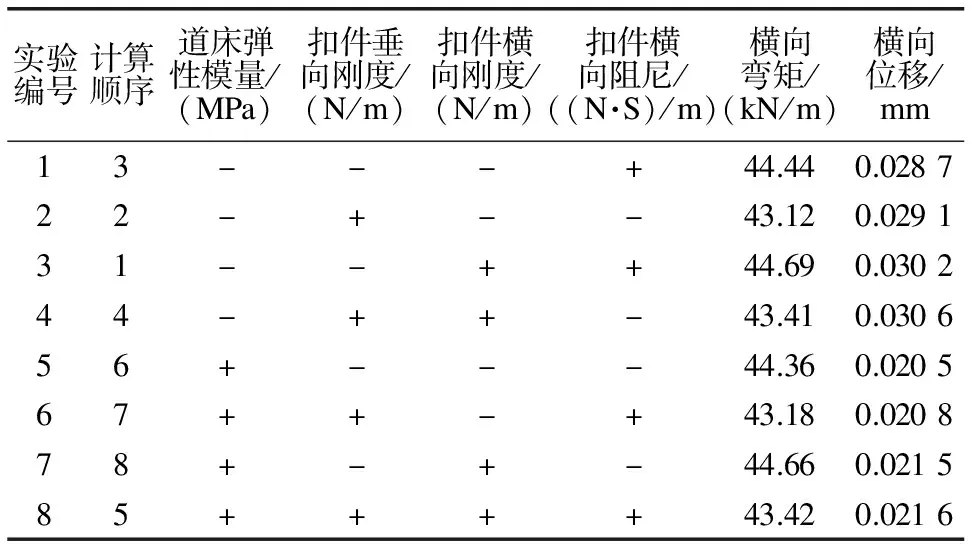
表3 24-1析因实验设计计算结果表

2.2 整体道床弯矩敏感性分析

将随机参数在8组不同水平下的取值代入模型中，计算在整体道床最不利位置处的最大横向弯矩，再对计算结果进行敏感性分析，得到随机参数的敏感性分析结果如图6所示。

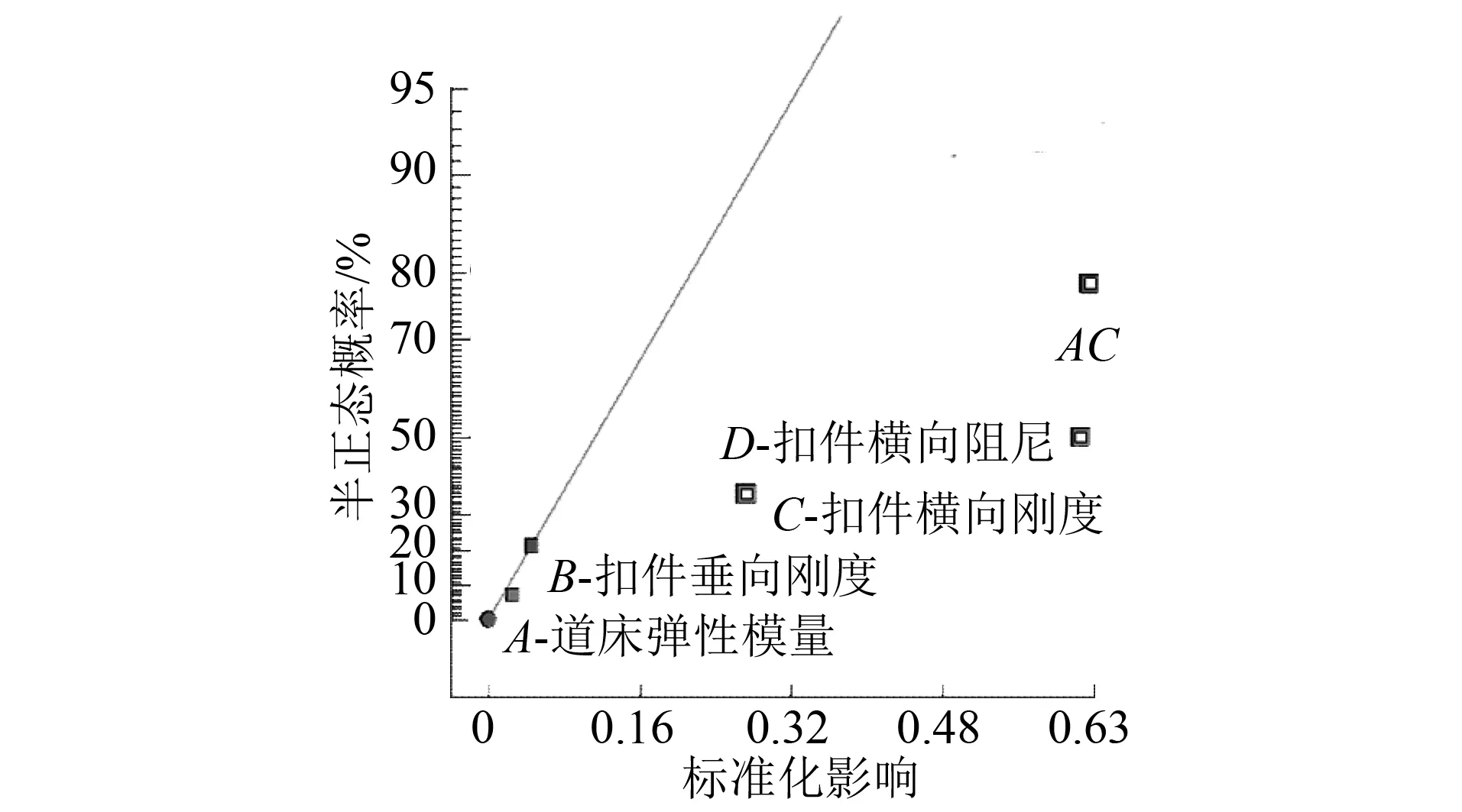
图6 24-1析因实验效应半正态概率图

在24-1析因实验效应半正态概率图中，用标准化效应值的绝对值作为横坐标，通过判断某个参数离直线的距离，判断不同因子的参数敏感性。在本文选定的4个待研究参数中，对整体道床横向弯矩敏感性从高到低排序为：道床弹性模量和扣件垂向刚度为比较敏感的参数，扣件横向刚度和扣件横向阻尼为不敏感参数。

图7为表示效应t值的帕累托图。从图中各效应所代表的柱形高度可直观地判断出各参数的敏感性：道床弹性模量、扣件垂向刚度和扣件横向刚度为敏感参数，扣件横向阻尼、道床弹性模量与扣件横向刚度的组合效应为不敏感参数。

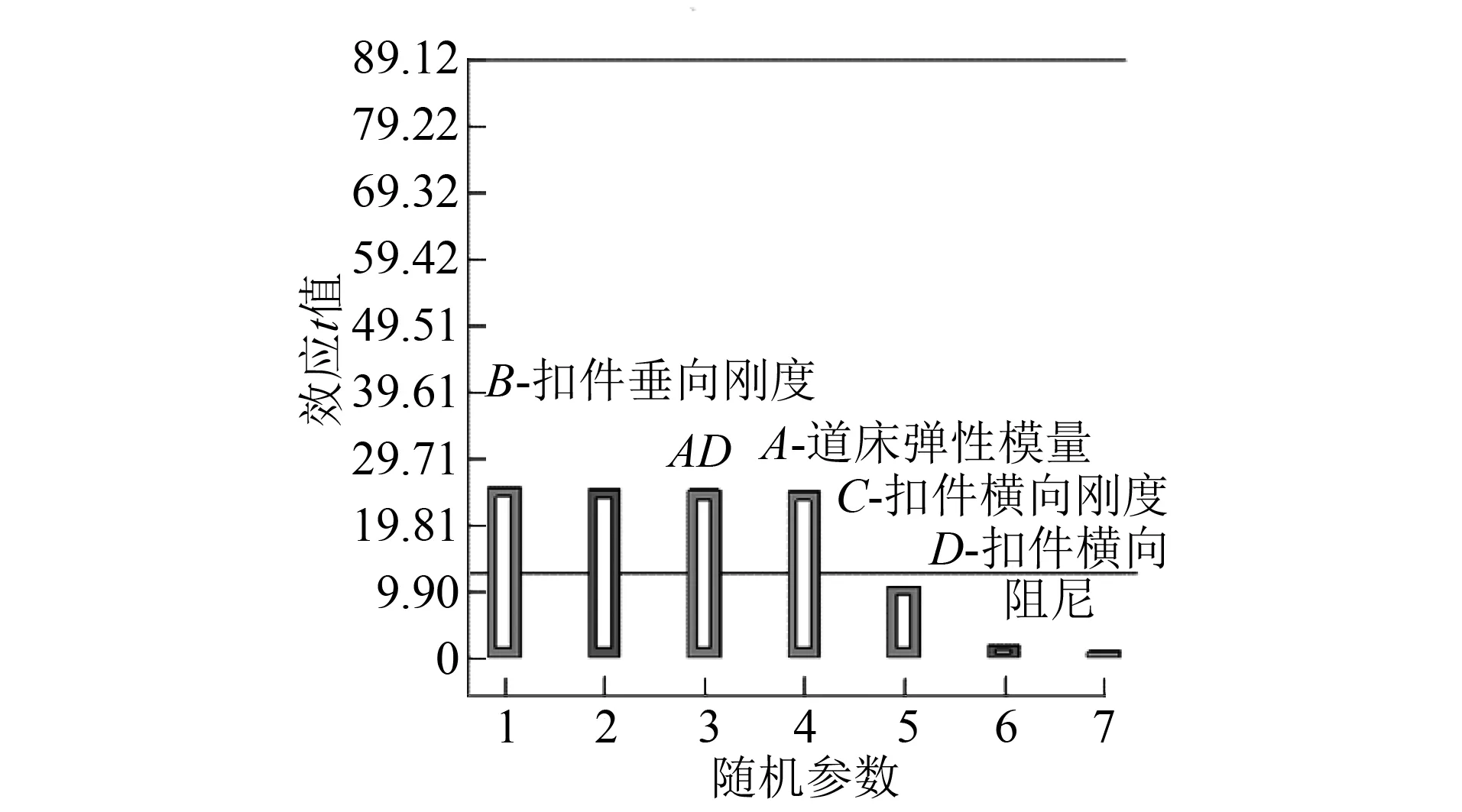
图7 24-1析因实验帕累托图

综合以上分析，4个随机参数对整体道床横向弯矩的敏感性从大到小排列为：道床弹性模量A、扣件垂向刚度B、扣件横向刚度C和扣件横向阻尼D。

3 内置式泵房轨道系统可靠度分析

本文使用中心复合设计方法(简称CCD法)对内置式泵房轨道系统的可靠度进行分析。主要考虑道床弹性模量A、扣件垂向刚度B和扣件横向刚度C这3个参数，分别计算有无内置式泵房时轨道系统的可靠度变化。

将随机参数取不同数值的15组平行试验的数据代入有限元软件中进行运算，记录每组试验中的道床横向弯矩值，通过数据分析软件拟合出道床横向弯矩的响应面，结果如图8～9所示。导出的响应面表达式为：

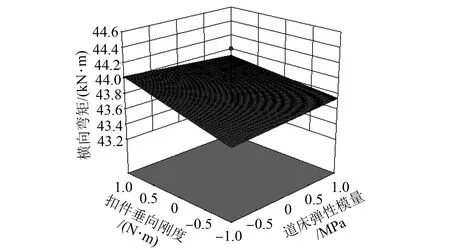
图8 有泵房时的道床横向弯矩响应面

横向弯矩(有泵房)

=43.84-0.354A+0.14B-0.17C-0.055AB+0.40AC+0.19BC

横向弯矩(无泵房)

=46.20-0.19A+0.11B+0.10C+0.10AB+0.11AC-0.19BC

图9 无泵房时的道床横向弯矩响应面

由极限状态方程定义，当限值-横向弯矩=0时，求出不同横向弯矩下对应的失效概率，相应的极限状态曲线图如图10所示。

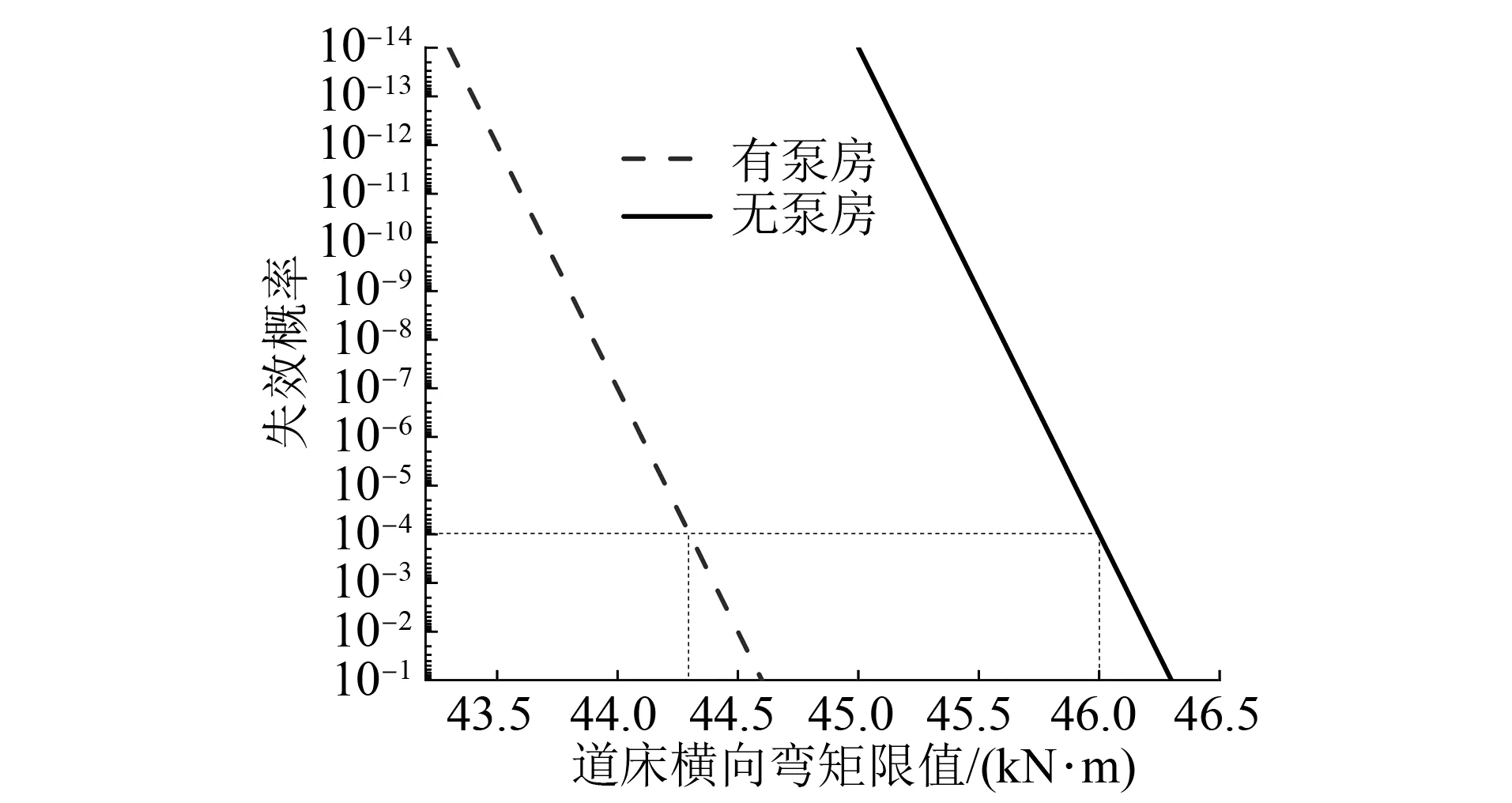
图10 横向弯矩-失效概率示意图

从图10中可以看出，在列车荷载作用下，失效概率相同时，有泵房的轨道系统比无泵房时的道床横向弯矩限值略小。根据文献[16]，将失效概率控制在10-4，可以在保证工程可靠度的同时尽可能降低结构造价，故本文将10-4作为结构失效概率的参考限值。此时，有泵房时的道床横向弯矩限值为44.3 kN·m，无泵房时的道床横向弯矩限值为46.0 kN·m，设置内置泵房使道床横向弯矩限值减少了仅3.7%。由此可见，道床设置泵房后对整体道床服役可靠性影响不显著。