不同轨道结构对地铁车辆轮周多边形不圆顺发展的影响

王伟铭 沈 钢 毛 鑫

(同济大学铁道与城市轨道交通研究院，201804，上海∥第一作者，硕士研究生)

城市轨道交通发展至今，乘坐舒适性已经成为了人们所关注的主要目标之一。但由于多种原因的影响，地铁车辆振动仍在不断加剧。除了钢轨波磨外，车轮的多边形磨耗也对车辆和轨道造成了很大的破坏[1-2]。文献[3]分析了车轮的非圆化磨耗进程，发现车辆的运行速度和轨道参数都影响着车轮的磨耗。文献[4]计算了高速车轮中动静不平衡的影响，发现动不平衡会进一步加速车轮失圆的发展。文献[5]研究发现车轮存在初始不圆顺后，车轮的垂向运动会随着车辆运行而不断恶化，使车辆轮周多边形进一步发展。文献[6]通过构建轨道系统的有限元模型，研究了簧下质量在轨道上的力与车轮低阶不圆顺之间的磨耗关系。文献[7]建立了车轮轮周磨耗预测耦合模型，预测了车轮轮周多边形不圆顺的发展过程，得到了车轮轮周不圆顺发展的规律。文献[8]在ABAQUS软件中建立了有限元弹性振动模型，对车辆通过小半径曲线和直线线路上的车轮轮周多边形不圆顺成因进行了分析。文献[9]借助有限元瞬时动态分析法，得到了车轮的摩擦自激振动加速了车轮多边形磨耗的发展。文献[10]认为轮对一阶弯曲共振是决定车轮多边形磨损波长的主要原因。文献[11]提出了基于冷作硬化的车轮多边形形成机理，并分析了磨耗发展规律。文献[12]分析了高速车辆中的车轮不圆顺与关键部件振动之间的关系。文献[13-14]通过建立刚柔耦合动力学模型分析了不同参数对轮轨力的影响。而这些文献都没有考虑轨下浮置板对车轮多边形的影响。因此，本文对车轮多边形下的轮轨间相互作用进行了探讨性研究，旨在分析浮置板对车轮多边形磨耗的影响。

1 地铁车辆车轮失圆实测情况

地铁车辆车轮失圆情形比较普遍，图1为实际测试的某地铁车辆车轮失圆廓形。

图1 实测车轮失圆廓形图

由图1可见，1位轮主要呈现1～3阶失圆，2位轮和4位轮主要呈现1阶偏心，3位轮主要呈现2阶的椭圆化。

图2为实际测量的车轮失圆粗糙度幅值图。其中，3位轮的情况最为严重，最大粗糙度超过了30 dB。

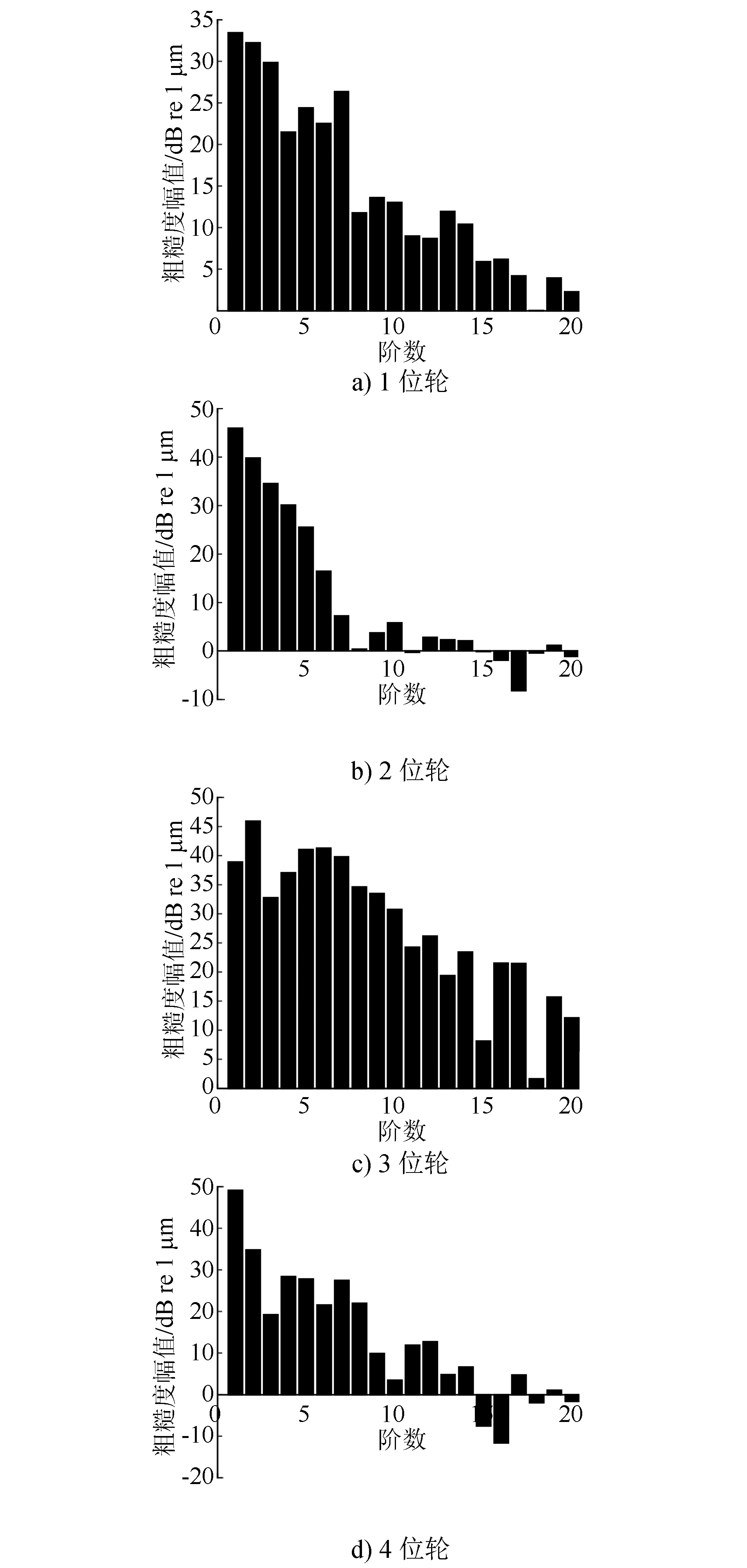
图2 实测车轮失圆粗糙度幅值图

2 轮对垂向耦合振动模型

为了更好地分析车轮磨耗功率与车轮周向径跳之间的关系，建立如图3所示的单自由度车轮-钢轨-浮置板垂向耦合振动模型，并作出如下假设：①一系弹簧刚度和阻尼参数以及轨下刚度阻尼参数均为常数；②钢轨为未磨耗的理想钢轨；③轮对和钢轨的位移均为因正压力引起；④仅考虑由于轮对失圆产生的径跳；⑤车辆运行速度恒定。

图3 单自由度车轮-钢轨-浮置板垂向耦合振动模型

其中名义滚动圆半径为R，不同时刻的实际轮径为R(t)；车辆运行速度为v；轮对中心的垂向位移为Z1，钢轨质心的垂向位移为Z2，浮置板质心的垂向位移为Z3；轮对质量为M1，钢轨局部质量为M2，浮置板局部质量为M3；一系垂向定位刚度为K1，阻尼为C1;轨下刚度为K2，阻尼为C2;浮置板局部垂向刚度为K3，阻尼为C3。地铁车辆车轮失圆主要呈现低阶多边形形式[6]，因此设置轮对初始多边形阶数为8。

以系统静平衡位置为坐标系原点进行建模，根据牛顿力学定律有平衡方程：

M1Z″1+C1Z′1+K1Z1=F

(1)

M2Z″2+C2Z′2+K2Z2=

-F+C2Z′3+K2Z3

(2)

M3Z″3+C3Z′3+K3Z3=

C2(Z′2-Z′3)+K2(Z2-Z3)

(3)

式中，F为轮对所受的动态法向力。

如果车轮具有任意不圆特点，则接触点位置的实际半径R(t)为：

Z2=Z1-R(t)

(4)

将式(4)代入式(1)、式(2)和式(3)并整理，有：

(M1+M2)Z″1+(C1+C2)Z′1+(K1+K2)Z1=

M2R″(t)+C2R′(t)+K2R(t)+C2Z′3+K2Z3(5)

M3Z″3+(C2+C3)Z′3+(K2+K3)Z3=

-C2R′(t)-K2R(t)+C2Z′1+K2Z1

(6)

而轮轨间的实际法向力还应加上轮轨间静平衡时候的法向力F0。

轮轨间蠕滑力T和蠕滑率ξ之间的关系如图4所示。该图像由线性段和饱和段组成，图中fN表示滑动摩擦力。而在不同正压力(即法向力)下，蠕滑力-蠕滑率之间的曲线也会随之变化，将正压力也作为一个自变量考虑，即可得到三维坐标系下的正压力-蠕滑力-蠕滑率关系图，如图5所示。

图4 蠕滑力-蠕滑率关系曲线

图5 正压力-蠕滑力-蠕滑率关系

根据不同正压力和蠕滑力，即可插值得到在该工况下的蠕滑率。当获得了接触点位置的蠕滑率和蠕滑力后，就可以根据式(7)得到轮轨接触点的瞬时摩擦功率Pr。

Pr=ξxTx·v

(7)

3 车轮圆周磨耗规律仿真

在SIMPACK软件中搭建单轮对-钢轨-浮置板垂向耦合振动模型[15]，如图6所示。将标准正弦八边形作为车轮圆周的输入，幅值为0.2 mm，可以得到如图7 a)所示的廓形示意图以及如图7 b)所示的圆周径跳与周向距离的关系。将模型中车辆运行速度设置为72 km/h。取轨下刚度K0=40 MN/m，轨下阻尼C0=5 000 Ns/m。

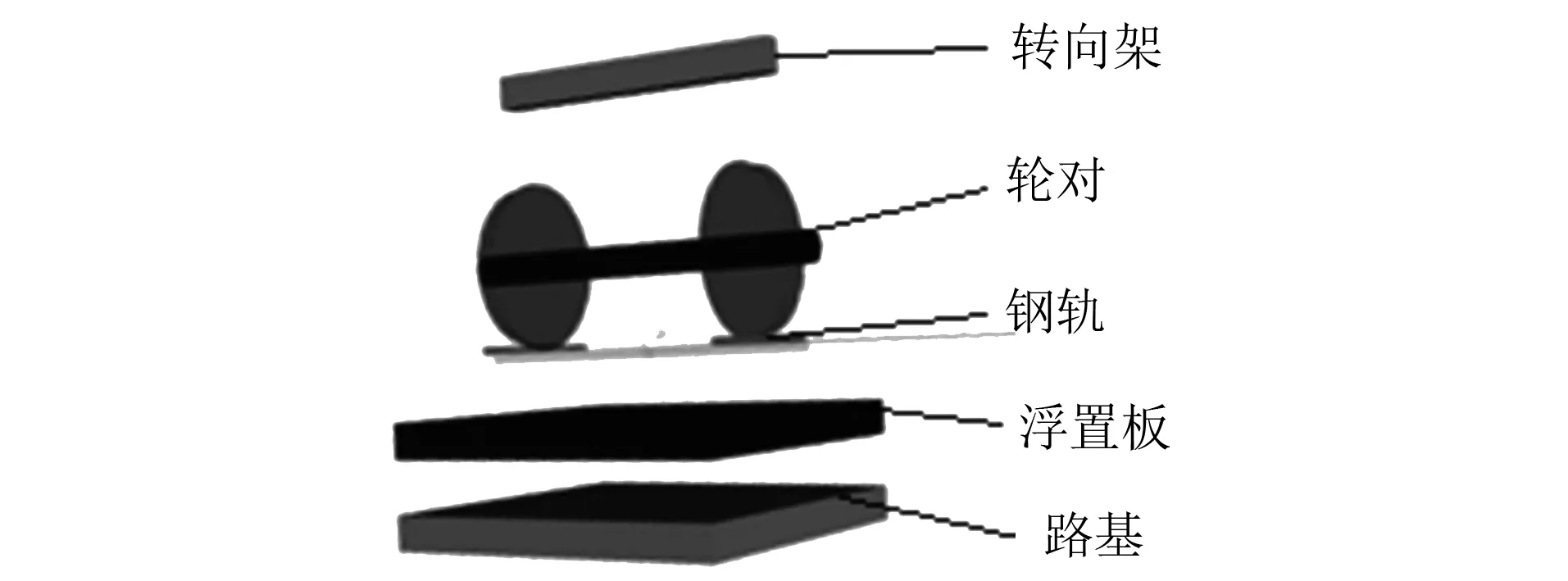
图6 单轮对-钢轨-浮置板垂向耦合振动模型

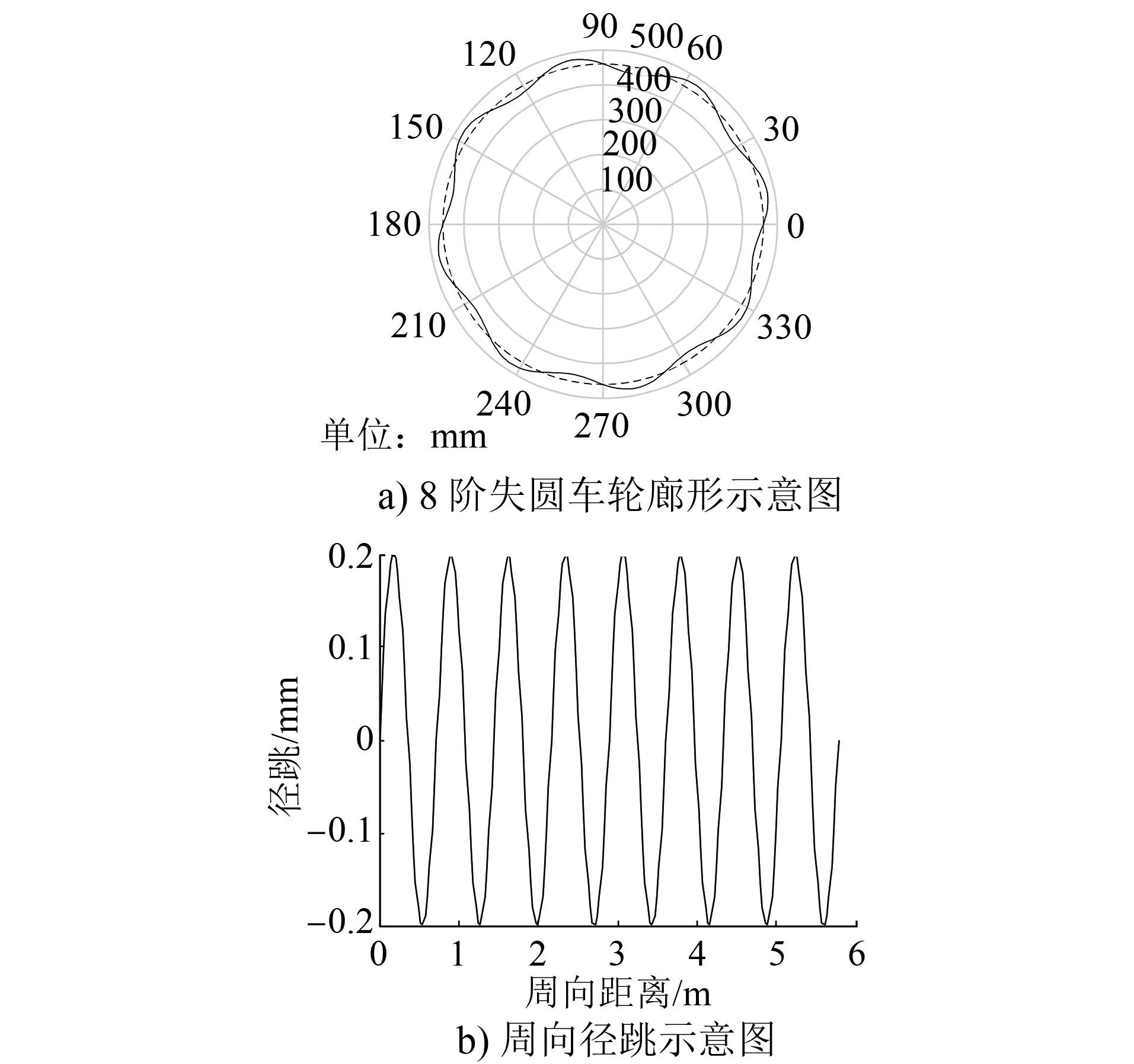
图7 失圆示意图

当轨下无浮置板时，车轮所受的正压力、蠕滑率和磨耗功率变化如图8～10所示。由图可见，径跳最高的位置正压力最大、蠕滑率最小、磨耗功率也最小，因此会加剧车轮的不圆顺现象。同时，为了检测浮置板在减缓车辆向路基的外力传递过程中所起的作用，输出路基所受的力与车轮径跳之间的关系图，如图11所示。

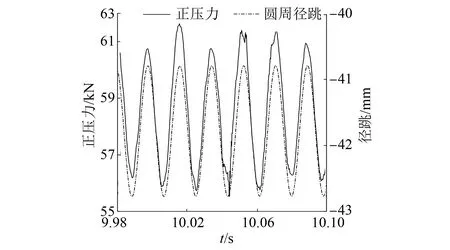
图8 正压力-径跳图(无浮置板)

图9 蠕滑率-径跳图(无浮置板)

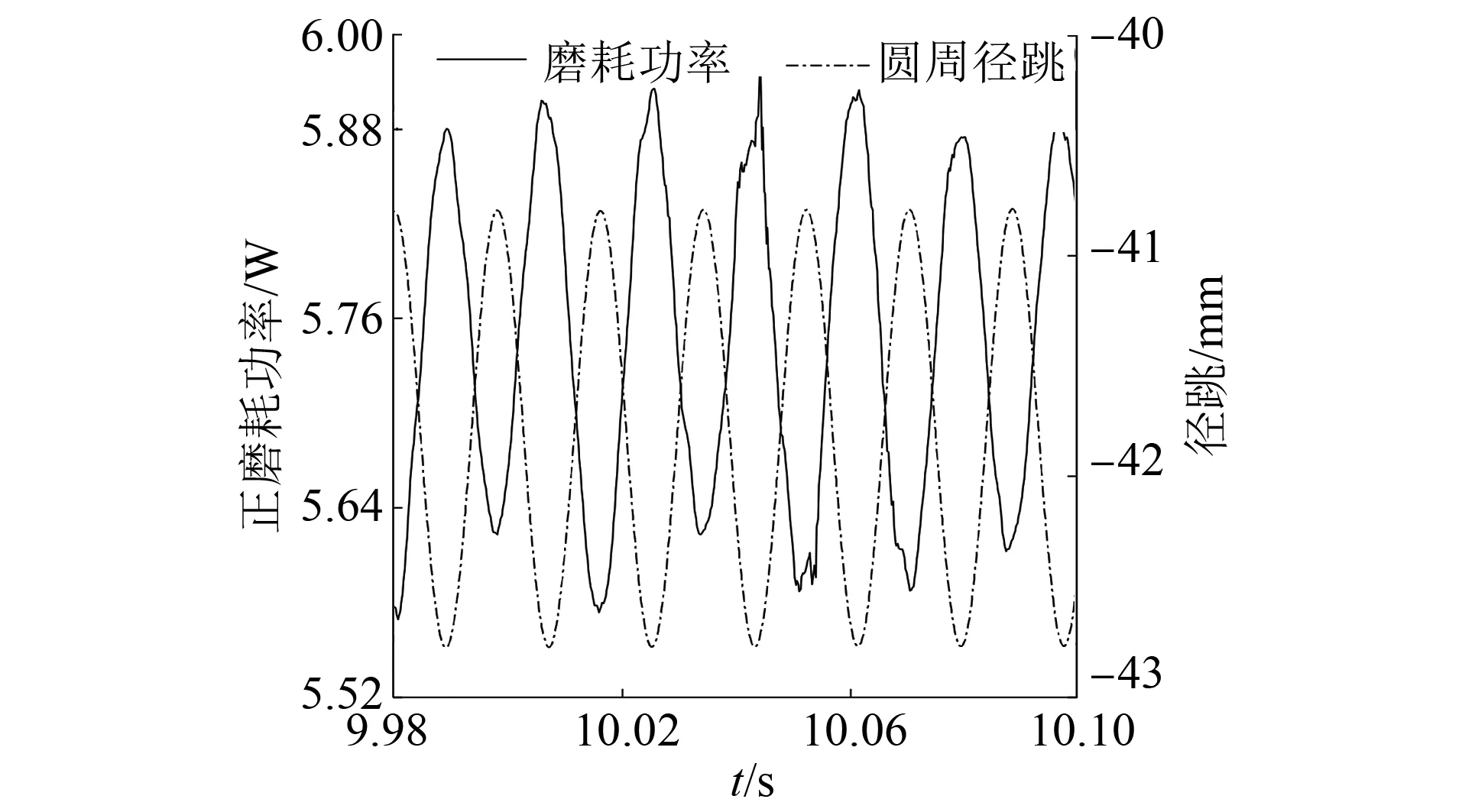
图10 磨耗功率-径跳图(无浮置板)

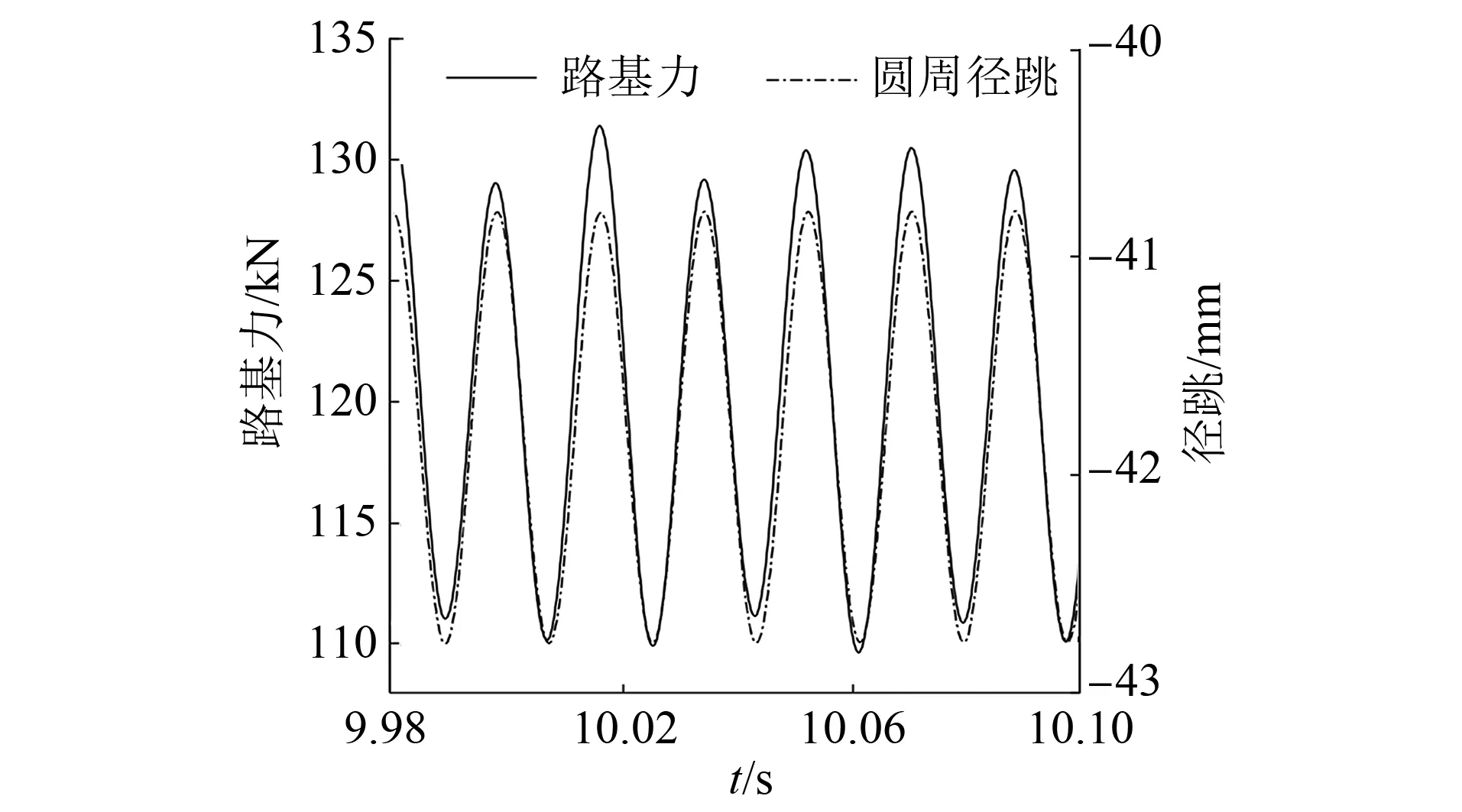
图11 路基力-径跳关系图(无浮置板)

设置轨下浮置板参数，然后进行仿真，得到车轮受到的正压力、蠕滑率和磨耗功率变化图如图12～14所示。由图可见，相较于车轮其他位置而言，径跳最高位置处所受的正压力仍然最大，蠕滑率与磨耗功仍然达到了极小值。由此可见，浮置板并不会改变车轮不圆顺的恶化趋势，但从数值上可以看出，与不加浮置板的相比，轮对在对应位置所受到的磨耗功率变小，这会减缓车轮不圆顺发展速度。图15为该模型下路基所受力的变化趋势，显然，浮置板可有效降低路基所受的振动。

图12 正压力-径跳图(有浮置板)

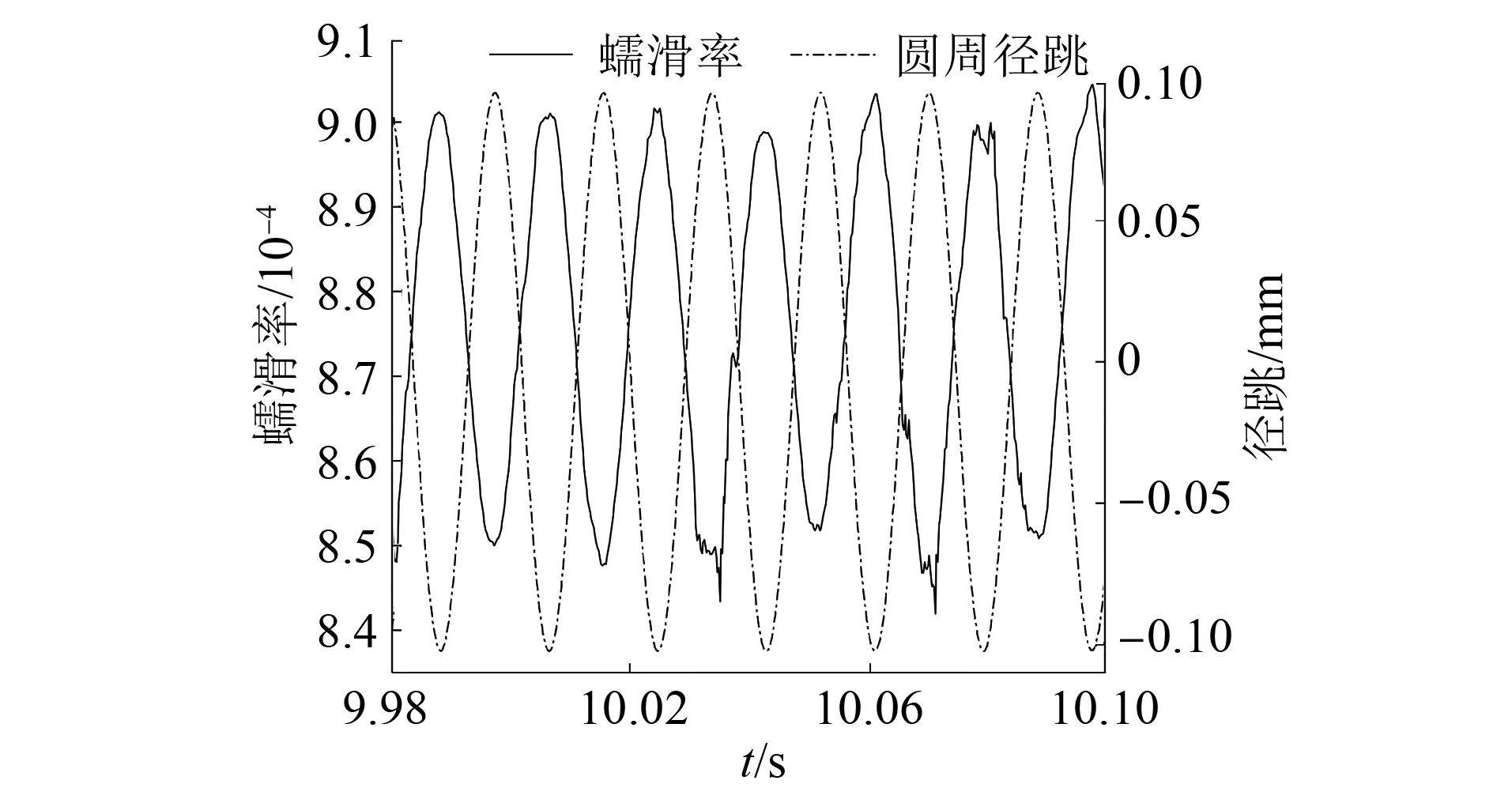
图13 蠕滑率-径跳图(有浮置板)

图14 磨耗功率-径跳图(有浮置板)

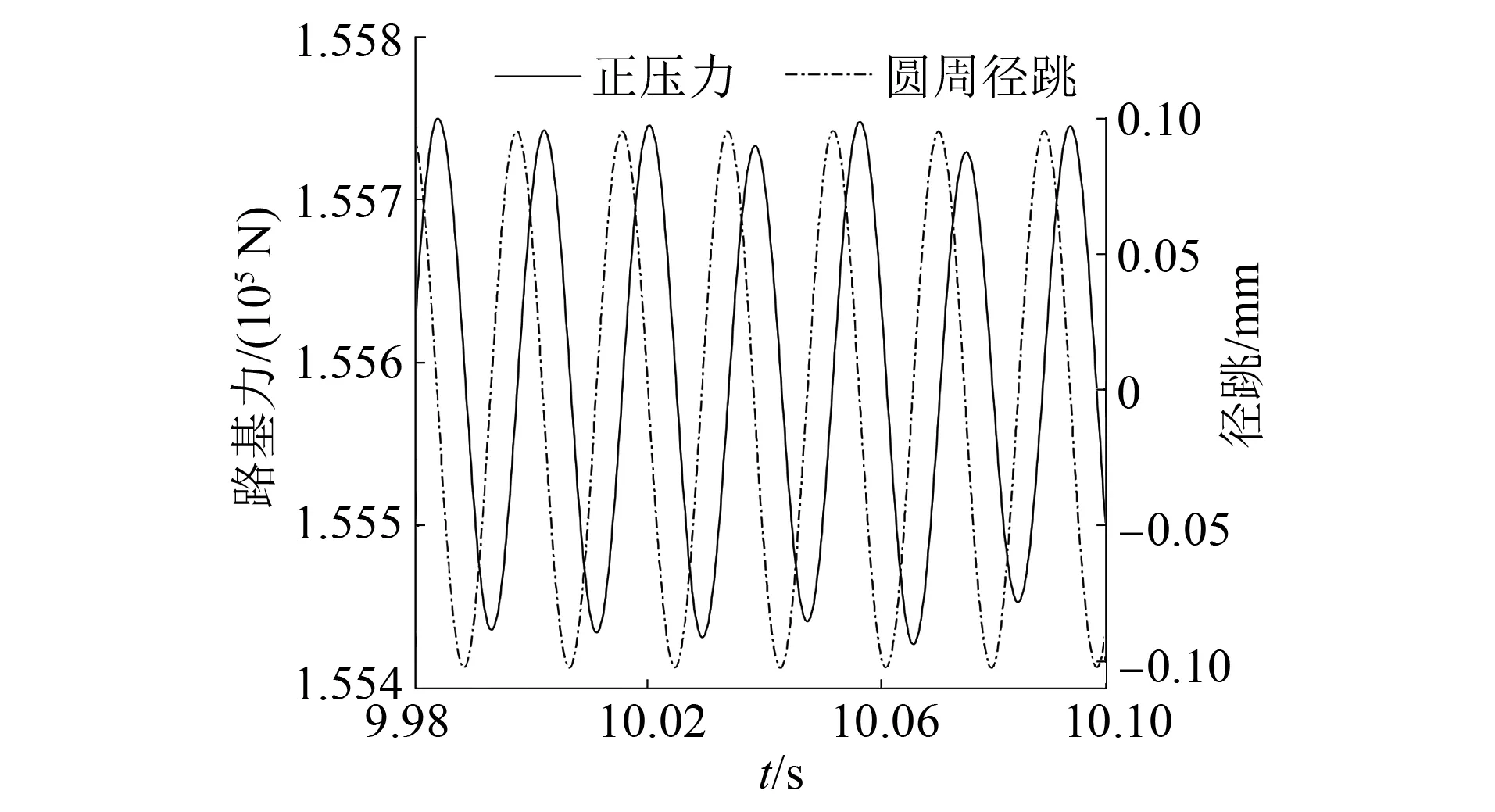
图15 路基力-径跳图(有浮置板)

为了探究不同浮置板刚度对车轮磨耗功率和路基力的影响，改变浮置板垂向刚度进行仿真，得到的对比图如图16～17所示。由图可见：当浮置板垂向刚度变大后，车轮所受的磨耗功率变大，但是相位没有发生偏移；而从路基所受力可见，随着浮置板垂向刚度的增大，路基所受力也增大，而且发生了相位的右移。

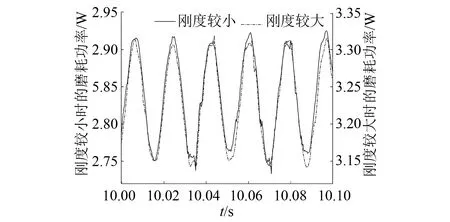
图16 不同浮置板垂向刚度的磨耗功率对比

4 结语

从不同轨道结构仿真结果可以看出：浮置板确实降低了路基所受到的振动；针对车轮不圆顺的发展，不论有没有浮置板，车轮不圆顺程度都会恶化；浮置板的存在会使车轮在相应位置的磨耗功率变小，这会减缓车轮不圆顺的恶化速率。由于浮置板的质量相较于车轮和钢轨的质量而言太大，其等效刚度和阻尼相较于一系弹簧和轨下刚度阻尼而言也太大，其参数近似于刚性；而改变浮置板的刚度参数，不会影响车轮所受的磨耗功率的相位但会影响路基受力的振动相位；随着浮置板刚度的增加，会导致磨耗功率变大，这会加剧车轮不圆顺的恶化趋势。因此，要想减缓车轮不圆顺的发展趋势，要从轨下参数的优化方面着手。

图17 不同浮置板垂向刚度的路基受力对比