基于最大一致容积Kalman滤波器的 多机器人协同定位

于镇滔，王忠庆，刘 鹏,2

(1.中北大学电气与控制工程学院，太原 030051；2.中北大学前沿交叉科学研究院，太原 030051)

0 引言

近年来，作为一项融合了测量、通信和计算等技术的新型智能测量单元群，无线传感器网络(Wi-reless Sensor Networks，WSN)成为了多个学科的研究热点，并且被应用于多个领域。根据WSN信息的不同传输方式，可以分为集中式和分布式。集中式通信在组网结构中通常包含一个中央融合节点，在融合计算时，该节点汇集了所有感知节点采集到的状态信息，其缺点是当该节点损坏或出现故障时，整个系统将停止运行。在分布式通信中，某一节点仅与其相邻节点进行信息互换，这种并行计算方式极大地缓解了单个传感器节点计算能力不足的问题，并提高了WSN系统面对故障时的鲁棒性。机器人系统拥有大量传感器，可视为一种可移动的无线传感器网络。通常所讨论的机器人定位是指通过所搭载的传感器来感知所处环境的相对位置、绝对位置信息以及环境信息，通过计算或信号处理将环境信息转换为位置信息，常见如温度、湿度和光照强度等。机器人定位系统从包含个体数量上可划分为由单个机器人构成的定位系统和由多个机器人构成的多机器人定位系统。在多机器人系统中，为降低传感器数量在融合计算中造成的经济负担，研究人员可通过减少测量所需的传感器种类来实现机器人群中个体间的差异化。所构成的多机器人系统通过任务分配和协同策略并行处理各自问题，进而提高工作效率。因为每个机器人所搭载的传感器种类不同，为传感器的选型留有较大空间。

单机器人系统定位的主要方法有全球定位系统、航迹推算法、路标定位等。航迹推算是利用机器人自身携带的里程计和惯性测量组合，利用上一时刻速度和航向角的状态信息，结合当前时刻速度和航向角测量值，估算出下一时刻的位置信息和航向角信息，但受累积误差的影响，定位精度会随距离和运行时间的增加而不断下降。为了解决误差累积问题，可以利用路标定位或者分布式估计算法给予其误差修正。相比单个机器人系统，多机器人系统可以修正已有定位方法，通过每个个体采集动态信息并分享数据给其余个体实现协同定位。这种协作方式极大地减少了单个机器人的能耗和对存储空间的消耗，并且当组内个别机器人发生故障时，整个系统仍可以继续完成任务，提高了系统的鲁棒性。

在多机器人系统数据传输和数据融合方面，将Kalman滤波算法与一致性思想相结合的分布式Kalman滤波算法已经得到了广泛的研究。W. Li等利用分布式Kalman滤波实现了基于绝对测量和相对测量的协同定位。之后不同研究者又相继提出了分布式扩展Kalman滤波和分布式无迹Kalman滤波。随着芯片级计算能力的提升，研究人员将注意力转向了传感器网络环境下分布式容积Kalman滤波的设计。J. Liu等利用五阶容积规则开发了一种分布式的容积Kalman滤波器来处理高阶估计问题，相比三阶规则，五阶规则更加精确和稳定。基于Kullback-Leibler散度，C. Hu等提出了一种分布式容积Kalman滤波器来解决协同跟踪空间物体问题，实验结果表明，分布式容积Kalman滤波器比分布式容积信息滤波器更为准确，但未给出具体原因。以上所研究的分布式算法多基于平均一致性思想，虽然其极大地减少了集中式算法的计算量，但无法在有限时间内实现精确一致性。为了解决此问题，本文将采用最大一致思想设计分布式容积Kalman滤波算法。在对最大一致问题的研究中，文献[12]提出了一种解决方案,减小了在选择最大状态估计值过程中加性噪声对结果的影响，提高了算法可靠性。文献[13]提出了一种用于在有限时间内实现平均一致性的算法，该算法提高了计算效率并且不需要在线内存。

机器人系统是一个典型非线性系统，分析并结合前面描述的不同定位算法，本文采用最大一致容积Kalman滤波器实现多机器人系统的协同定位。通过图论来刻画机器人节点间的数据传输方式，将光电传感器和偏振光传感器采集的数据进行数据融合，以减少累积误差带来的影响。

1 问题的描述

本节首先对单个机器人运动系统进行运动学建模，然后描述多个机器人节点之间的通信拓扑图。

1.1 单机器人运动学模型

本文选择麦克纳姆轮机器人作为两类传感器的载体。机器人在正常运行时，载体系的原点与机器人的质心相重合，并且令机器人运动方向为轴正方向，平行于地面沿轴正方向顺时针旋转90°得到轴正方向，以轴正方向和轴正方向的叉乘结果作为轴正方向。使用初始时刻的载体系作为机器人在整个运动过程中的全局系。在移动过程中，机器人所搭载的传感器对应的测量坐标系与载体系重合。

多机器人系统中每个个体在全局坐标系中的位置为=[,,]和姿态四元数为=[,,,]，其中为标量值，假设、、分别为三维空间坐标系中3个坐标轴正方向上的单位矢量，则、、分别为对应的标量值，即=+*+*+*；速度向量可表示为=[,,]，则机器人的状态信息可以表示为=[,,]。时刻机器人运动学方程如式(1)所示

=(-1)+-1

(1)

其中，函数(·)如式(2)所示

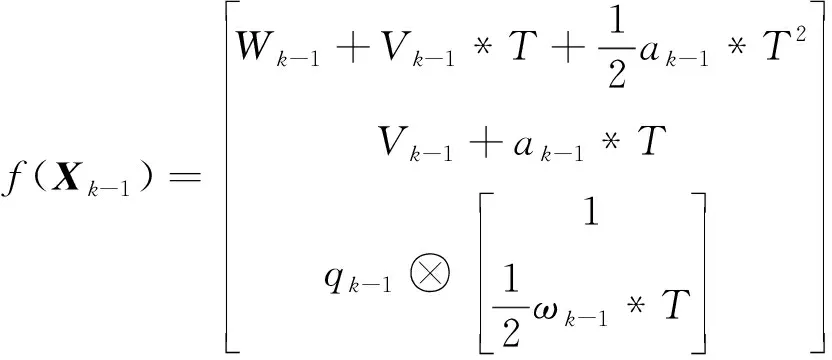
(2)

其中，-1表示均值为0、方差为-1的过程噪声。

在移动过程中，机器人系统可以通过传感器采集自身状态信息或环境信息。但是受设备精度的影响，测量值在真实值上下波动。偏振光传感器可仿照昆虫，利用天空偏振光导航的原理进行光学辅助导航。时刻偏振光传感器的测量方程如式(3)所示

,=+

(3)

其中，为时刻的航向角；为服从均值为0、方差为的测量噪声。光流传感器的测量方程如式(4)所示

,=V+

(4)

其中，矩阵表示全局系到载体系的坐标变换矩阵；表示均值为0、方差为的测量噪声。通常复杂机器人系统将式(3)和式(4)的测量以集中式的方式叠放在一个观测矩阵中。本文将两种传感器分别配置于不同的机器人，这不仅可以降低机器人的硬件成本，而且有利于减少计算过程所需的存储量。

1.2 多机器人系统通信描述

假设多机器人系统由个机器人构成，其可以定义为图=(,)。将系统中的单个机器人视为一个节点。定义={,,…,}为节点集合，⊆×是信息在个体间传递的通道集合，并且定义个体的邻居由={|(,)∈}表示。在其邻居内，个体的入邻居和个体的出邻居如图1所示。个体的入邻居数量由入度=||决定，而其出邻居数量由出度=||决定，其中={|(,)∈}，={|(,)∈}。

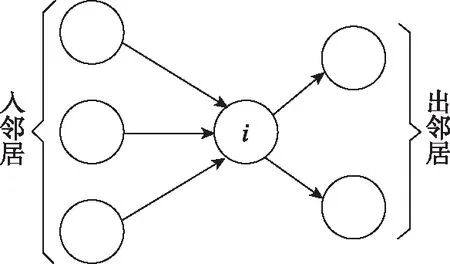
图1 入邻居和出邻居定义Fig.1 The definitions of in-neighborhood and out-neighborhood

在多机器人系统中，传感器采集的本地信息与入邻居所传递的数据进行融合，再将融合后的信息传递给出邻居。本文将采用一致性算法实现此数据融合过程。一致性算法可以大致分为平均一致性和最大一致性。平均一致性是求取数据集的平均值，具体形式如式(5)所示

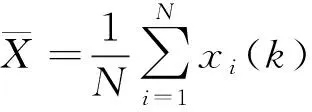
(5)

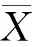
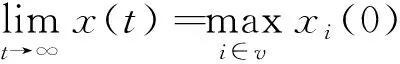
(6)

其中，(0)表示第个传感器的初始值；代表个体集合。

2 容积Kalman滤波器及分布式形式

为解决多机器人系统在移动过程中的状态估计问题，本文采用基于最大一致的容积Kalman滤波算法予以解决。本节第一部分简单介绍容积Kalman滤波算法，并以其为框架得到容积信息滤波算法；第二部分介绍基于最大一致的容积Kalman滤波算法。

2.1 容积Kalman滤波器

在非线性Kalman滤波的测量更新时，状态值、误差协方差、自相关协方差和互相关协方差都具有“非线性函数×高斯密度函数”形式的高斯积分计算，具体如下

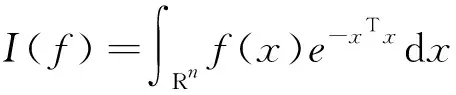
(7)

其中，函数()为被积函数与部分高斯分布函数的乘积；R为积分域；(·)表示矩阵的转置。

为了解决以上问题，I.Arasaratnam和S.Haykin使用三阶球面容积法则来近似高斯积分。具体计算过程见参考文献[15]，利用球面—径向容积准则得到如下结果

(8)

以容积Kalman滤波器为基本框架，采用统计线性误差传播方法，并以近似的方式表示扩展信息滤波器中的雅可比矩阵，从而得到容积信息滤波器。

当初始化和时间更新部分不变时，测量更新中的误差协方差矩阵|-1、自协方差矩阵,|-1和互协方差矩阵,|-1可改写如下

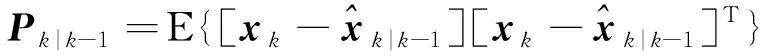
(9)

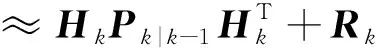
(10)

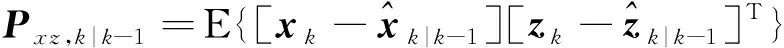
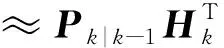
(11)

其中

=[(|-1),|-1]

=(,|-1)(|-1)

(12)

从而由扩展信息滤波器算法可知,容积信息滤波器的信息矩阵和信息向量表示如下

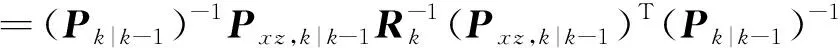
(13)

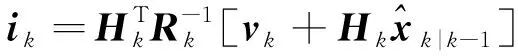
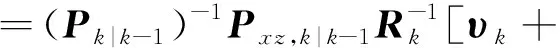
(14)

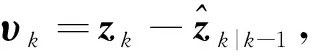
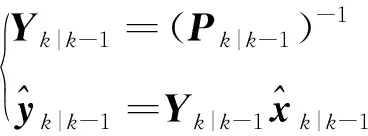
(15)

进而得到信息矩阵和信息状态矢量的更新方程为

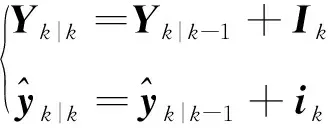
(16)

2.2 最大一致容积Kalman滤波算法

由个异构机器人构造的多机器人系统，每个个体的观测方程不同，具体表述如下

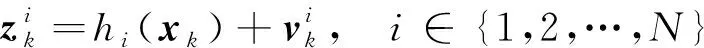
(17)

由式(17)可以得到等式(13)和式(14)中相关向量的表达形式，具体如下：

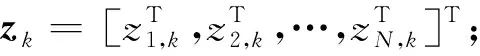
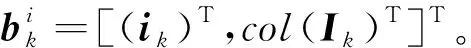
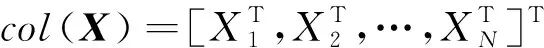
(18)

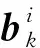
表1 最大一致容积Kalman滤波

3 仿真

这一节通过麦克纳姆轮机器人验证文中提出算法(记为DMKF)的效果，与其进行比较的是基于平均一致容积Kalman滤波器(简称DAKF)和集中式容积Kalman滤波器(简称JCKF)。

3.1 参数设置

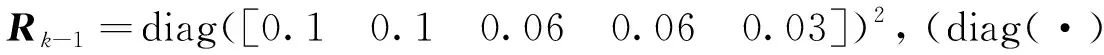
对于集中式容积Kalman滤波算法，其观测方程如下

(19)

对于分布式容积Kalman滤波器，第一组机器人S1和S2的观测方程为

,=+

(20)

其中，=006,=1,2。第二组机器人S3和S4的观测方程为

,=+

(21)

其中，=01,=1,2。令表示状态值,初始值为=[0,0,10,0,45°]，初始的协方差矩阵=diag([1,2,1,2,05°])。机器人间的信息传输关系如图2所示。

图2 异构机器人系统信息传输关系图Fig.2 Information transmission diagram of heterogeneous robot systems

3.2 结果与讨论

通过仿真，得到了基于JCKF、DAKF和DMKF算法的多机器人协同定位结果。令机器人S1的数据代表整个系统的状态，其沿预先设计的轨迹运动。位置状态信息估计的结果如图3所示。与真实轨迹结果进行对比，轨迹的均方根误差如图4所示。本文将方向角的估计值与真实值之差作为方向角误差，如图5所示。

图3 定位结果 Fig.3 Location results

图4 轨迹误差对比Fig.4 Comparison of trajectory errors

图5 航向角误差对比Fig.5 Comparison of heading angle error

由图3可知，基于DMKF协同定位所产生的折线与真实轨迹重合度较高，误差基本稳定在0～12.3533m之间。而对于DAKF所代表的折线，相较于DMKF所代表的折线其定位效果较差，每段路程中都有较大偏离。在图4中，前200次定位误差波动剧烈，最大误差为19.4265m；后200次定位误差波动减小，但没有收敛的趋势。对于JCKF所代表的折线，全程仅有几段定位估计与真实轨迹重合，是三组定位中最差的一条。由图4可知，其定位误差在前300次迭代中保持上升趋势，最大误差为16.2072m，之后逐渐下降，但误差依然保持在高位。

从图5可得，JCKF算法的方向角在整个定位过程中误差较小，误差范围基本保持在[-6.9887，5.2885]，但在转弯时波动较大。与此相比，DAKF算法的方向角误差范围为[-3.2815，12.2235]，DMKF算法的方向角误差范围为[-5.3972，6.5912]，与JCKF算法的方向角误差范围相近，但无较大波动。

4 实物仿真

为了验证算法1在协同定位中的可行性，本文通过构建机器人系统进行验证。采用麦克纳姆轮机器人作为平台，通过上位机对机器人系统进行控制，如图6所示。运行结束后，取其中一个机器人的运行数据进行曲线拟合，如图7所示。通过多次测试，验证了携带单一传感器的多个机器人可采用该算法实现协同定位。

图6 麦克纳姆轮机器人和上位机界面Fig.6 Mecanum wheel robot and PC interface

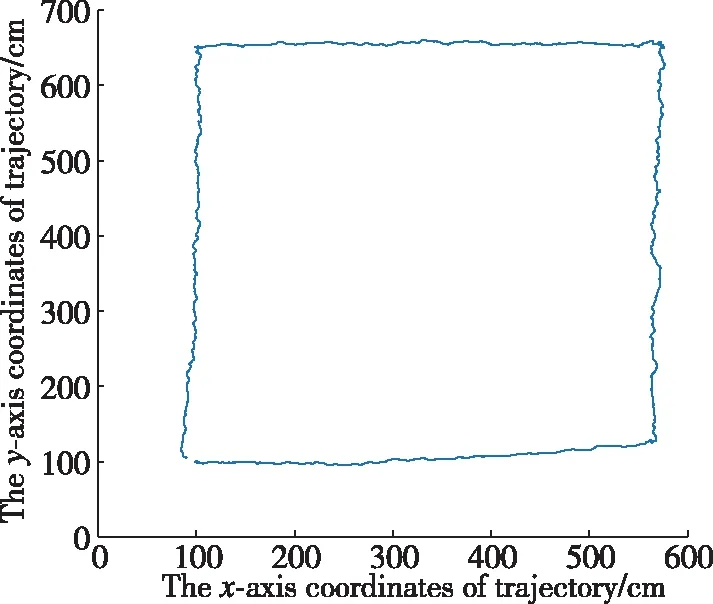
图7 实物仿真轨迹图Fig.7 Physical simulation trajectory

5 结论

本文提出了一种配置单一的多机器人协同定位策略，该策略采用容积信息滤波算法分别将本地观测信息和邻居观测信息进行融合。通过最大一致性思想得到全部个体的最大信息矩阵和信息向量，经过状态更新获得下个时刻的状态值。通过比较集中式容积Kalman滤波算法和平均一致容积Kalman滤波算法，得到以下结论：

1)基于平均一致容积Kalman滤波算法无法在有限时间内达到一致性，导致系统定位误差较大，而基于最大一致的容积Kalman滤波器正好弥补了这一点。相比集中式容积Kalman滤波算法的轨迹误差和方向角误差，基于最大一致的容积Kalman滤波算法在滤波效果和稳定性上都有较好的表现，并通过多次实物测试验证了最大一致容积Kalman滤波算法可实现多机器人协同定位。

2)将搭载多个传感器的单个机器人拆解为多个携带单个传感器的异构机器人。通过任务分配和数据共享，可以降低单个机器人的计算量，并且不会降低整个系统的定位性能，这可以降低因为追求高精度定位而选购昂贵传感器所造成的高额费用。