基于排列熵的长时间序列复杂程度分析

2022-02-18陈强强戴邵武吕余海

导航定位与授时 2022年1期

陈强强，戴邵武，吕余海，张刚

(1.海军研究院，上海 200436；2. 海军航空大学岸防兵学院, 烟台 264000)

0 引言

光纤陀螺作为重要的惯性传感器之一，能够有效进行角速度测量，在导航、制导领域有着广泛的应用。在光纤陀螺工作过程中，受到工作环境、温度变化等影响，导致光纤陀螺输出信号具有强烈的非线性、非平稳性，从而使其时间序列信号具有较强的复杂性。通过对光纤陀螺输出信号进行复杂性计算，能够分析其时间序列内部作用机制，从而研究信号的系统规律。文献[2]通过对光纤陀螺漂移数据分量信号进行复杂性分析，得到高频噪声项及混合模态分量，完成对光纤陀螺原始含噪信号的去噪。文献[3]以排列熵作为衡量信号复杂度的工具，得到信号复杂度与回归精度之间的关系，实现对光纤陀螺温度漂移的建模及补偿。文献[4]通过比较分解后数据与原始输出数据之间的复杂程度关系，验证了分解算法能够有效降低光纤陀螺输出序列的复杂程度，从而提高光纤陀螺随机误差的预测精度。通过对光纤陀螺输出序列进行复杂度分析，能够把握数据规律；同时，光纤陀螺输出序列的复杂度信息也可作为时间序列的特征信息，为后续进行光纤陀螺输出信号识别、故障诊断、预测研究等方面奠定基础。

在对时间序列复杂度进行分析的过程中，由B. Christoph等提出的排列熵算法是一种有效监测时间序列随机性和动力学突变行为的方法，其计算方法简单、抗噪能力强，适用于非线性、非平稳的光纤陀螺输出序列，在对陀螺仪输出信号分析、机械系统(滚动轴承、齿轮箱等)振动信号分析及医学信号(肌电信号、脑电信号等)复杂度分析中有着广泛的应用，相比传统的时频特征具有明显的优势。但在排列熵的解算过程中，时间序列的长度对排列熵值影响较为明显；同时，对长时间序列进行排列熵求解时，运算量较大，计算时间较长，降低了时间序列分析的效率。

光纤陀螺输出时间序列通常为长时间序列，为了有效度量长时间序列条件下的光纤陀螺输出序列复杂度，并提高排列熵算法的计算效率。本文通过引入经验模态分解中的迭代思想及包络算法，利用三次样条插值算法求取原始长时间序列的上下包络曲线，得到上下包络均值作为慢振荡分量；在求取上下包络曲线时，将原始时间序列长度限定为求解排列熵信息的通用长度，既避免了因时间序列长度过长而无法准确度量复杂度，同时优化了解算流程，提高了计算效率。

1 排列熵算法分析

排列熵算法原理为：针对长度为的时间序列{(),=1,2,…,}，对()进行相空间重构

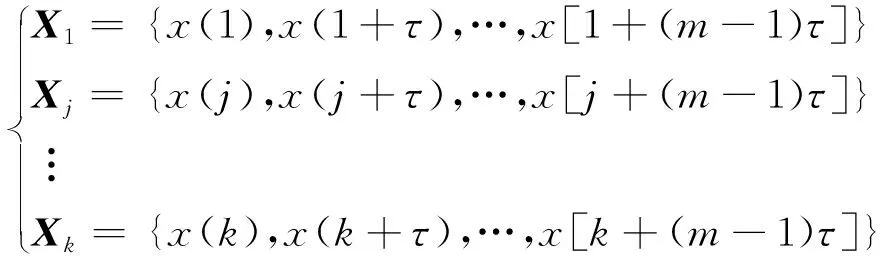
(1)

式中，为嵌入维数；为延迟时间；=-(-1)为重构向量的个数。

将中的元素按升序排列得

[+(-1)]≤…≤[+(-1)]

(2)

式中，,,…,为各元素在排序之前位于相空间所在列的索引。

若中有两元素相等，则按原始顺序排列。通过对相空间重构后的时间序列进行分析，对于任意一个，均能得到相应的符号序列={,,…,}，其中，=1,2,…,，且≤!。可定义排列熵为

(3)

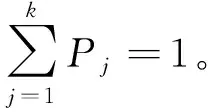
(4)

此时，的取值为[0,1]，可反映出时间序列的复杂程度，越大，则序列复杂程度越高。

排列熵作为衡量时间序列内部复杂度的算法，计算过程简单方便，能够有效地分析非线性、非平稳信号，适用于光纤陀螺输出信号。在排列熵的计算过程中主要包括3个参数：时间序列长度、嵌入维数、延迟时间。排列熵算法的提出者Bandt建议选择嵌入维数为3～7，且一般随着时间序列长度的增加进行相应调整；延迟时间对时间序列的计算影响较小，一般选择=1。后续学者在对时间序列进行排列熵分析时，对参数的选择进行了总结归纳，对于时间序列长度=2048的时间序列，取=6，=1。

在光纤陀螺输出信号采集过程中，当时间序列长度过长时，使用常规排列熵算法进行复杂程度衡量需要考虑以下问题：1)如果时间序列长度为2(=2048)时，相应的参数应该如何选择？此时嵌入维数的取值如果过大，则在式(1)中的相空间重构过程会均匀化时间序列，从而忽略时间序列中的微弱变化。2)时间序列长度的增加，增加了排列熵解算时长，在对光纤陀螺输出信号的实时分析、惯导故障实时诊断过程中降低了计算效率。3)在长时间序列条件下，不同长度的时间序列所对应的嵌入维数选择也有所不同，此时需要选择并调整相应的嵌入维数，以降低排列熵解算过程的自适应性。

2 均值排列熵算法

2.1 包络均值思想

在排列熵算法的分析中，针对长时间序列的复杂程度计算过程中存在的问题，提出了一种基于包络均值思想的均值排列熵算法。用包络均值信号代替复杂的原始信号，使其适用于非平稳信号分析。

包络均值思想源自经典的时频分析算法—经验模态分解(Empirical Mode Decomposition，EMD)。EMD算法能够根据信号特点自适应地将信号分解成一组具有物理意义的固有模态函数，在非线性、非平稳时间序列分析中得到广泛应用。

EMD方法在分解的过程中，首先找出信号的全部极值点，然后利用三次样条插值方法求取上下包络曲线，并定义信号的局部包络均值为慢振荡分量。在对上下包络曲线进行三次样条插值的过程中，可通过固定端点完成对包络均值时间序列长度的确定，从而将长时间序列的排列熵求解问题转换为固定时间长度的复杂度求解。

2.2 均值排列熵

基于此，定义均值排列熵算法如下：

1)针对长度为*(=1,2,…,)的原始信号()，确定()的所有极大值点与极小值点，通过三次样条插值方法，确定拟合后的时间序列长度，对()的极值点进行拟合，其极大值点的拟合曲线组成上包络线，其极小值点的拟合曲线组成下包络线。

2)计算与的均值，记为包络均值曲线。在EMD的计算过程中，定义为慢振荡分量。通过不断减去慢振荡分量可以完成对快振荡分量的筛选，因此在均值排列熵的计算过程中，选择采用慢振荡分量代替原始时间序列信号。

3)计算包络均值曲线的排列熵，得到均值排列熵值。

基于包络均值思想的均值排列熵算法如图1所示。

图1 均值排列熵算法流程Fig.1 Flow of mean permutation entropy algorithm

文献[11,16]对时间序列信号进行排列熵分析，选择时间序列长度为2048，因此本文在计算过程中，选择时间序列长度为2048的倍数进行对比。算法流程图如图1所示，采用均值排列熵算法代替常规排列熵算法，对光纤陀螺原始长时间序列进行复杂度求解时，通过选择均值包络曲线代替原始数据进行排列熵求解，在对上、下包络曲线进行三次样条插值时限定了时间序列长度，避免了因时间序列过长导致排列熵计算过程中嵌入维数、时间延迟参数无法准确选择的问题，同时减少了时间序列长度，提高了解算效率。

3 仿真验证

为了验证本文提出的均值排列熵算法对长时间序列的复杂度计算问题，选择光纤陀螺输出信号作为原始数据进行验证。在常温条件下对陀螺组件进行性能测试，采样频率4Hz，输出单位为(°)/h，选取某一温度下的，长度为4096(=2×2048)的一组光纤陀螺静态漂移数据，如图2所示。

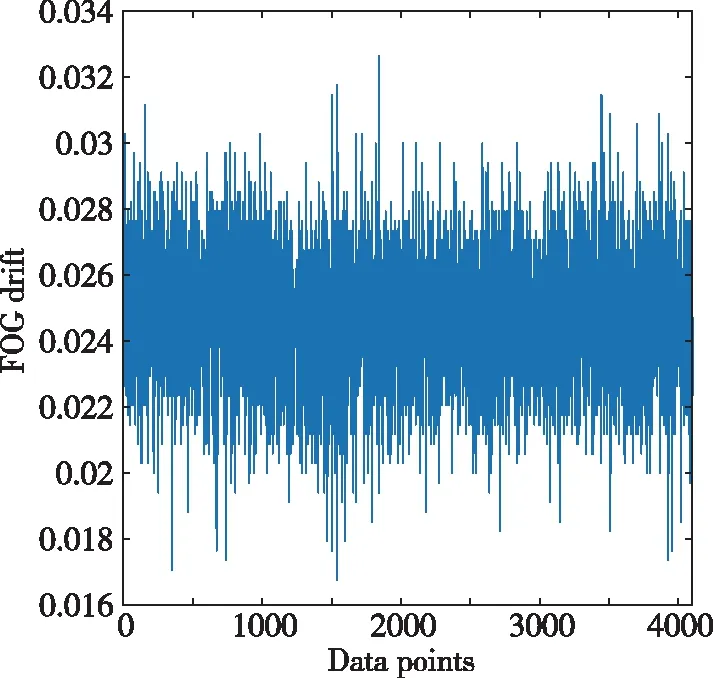
图2 光纤陀螺的原始信号(N=2×2048)Fig.2 The original signal of FOG(N=2×2048)

设置三次样条插值后的时间序列长度为2048，对得到的原始时间序列进行上、下包络曲线求解，得到均值包络曲线如图3所示。

图3 原始信号的包络曲线Fig.3 Envelope curve of the original signal

分别对上、下包络曲线，均值包络曲线及原始信号数据进行排列熵求解，并统计单次计算排列熵的时间，得到结果如表1所示。

表1 排列熵结果(N=2×2048)

如表1所示，上、下包络曲线与均值包络曲线的排列熵值相近，且计算效率相似。对于长度为=2048的光纤陀螺输出信号，取=6，=1更能准确表达其排列熵值，避免了参数选择过程，提高了计算效率。

为了继续验证均值排列熵算法对长时间序列的复杂度计算问题，选取某一温度下的，长度为6144(=3×2048)的一组光纤陀螺静态漂移数据，如图4所示。

图4 光纤陀螺的原始信号(N=3×2048)Fig.4 The original signal of FOG(N=3×2048)

设置三次样条插值后的时间序列长度为2048，分别对上、下包络曲线，均值包络曲线及原始时间序列进行排列熵求解，并统计单次计算排列熵的时间，得到结果如表2所示。

表2 排列熵结果(N=3×2048)

排列熵的取值范围为[0,1]，其取值越大表示时间序列的复杂程度越高，对比表1和表2可知：1)对于长度为4096及6144的光纤陀螺输出序列而言，采用常规排列熵算法进行复杂程度分析，其差值仅为0.0054，无法有效区分不同时间序列之间的复杂程度；2)以均值包络曲线的排列熵值作为光纤陀螺输出信号的复杂度衡量，针对长度为6144(=3×2048)的时间序列，能够准确反映其排列熵值并提高计算效率；长度为6144(=3×2048)的光纤陀螺输出信号复杂程度大于长度为4096(=2×2048)的光纤陀螺，符合排列熵的客观规律，验证了均值排列熵的可行性。同时，由于均值排列熵算法确定了均值包络曲线的长度，避免了在排列熵解算过程中的嵌入维数选择问题，提高了算法的自适应性。